工字型BRB核芯构造对承载力影响的研究

周 珺

(上海申核能源工程技术有限公司，上海 200033)

1 研究背景

某实际工程的工字型BRB外观尺寸为300 mm×300 mm，长4 m，主要由内芯钢材、钢套管和填充料组成。内芯钢材和填充料间存在无粘结材料，它可以使接触面无摩擦力，轴向荷载由内芯钢材承担。同时该材料有一定体积，在钢板受压时，由于泊松比原因需要一定变形空间，这时无粘结可膨胀材料受到挤压给内核心钢提供变形空间。本文针对BRB内芯钢材厚度、外套筒厚度、无粘结材料厚度的影响做模拟分析。建立同力学试验相符的有限元模型，将影响因素组合变换进行模拟，分析各因素的影响关系。

2 静力拉压试验

本文所选的工字型BRB的静力拉压试验(如图1所示)设定：依次按1/300，1/200，1/150，1/100变形反复拉压各3次，按设计要求，屈服承载力设计值4 500 kN，最大承载力6 750 kN，试验最大变形40 mm。图2记录了拉压双向的本构滞回曲线，即本文研究所模拟的本构曲线。

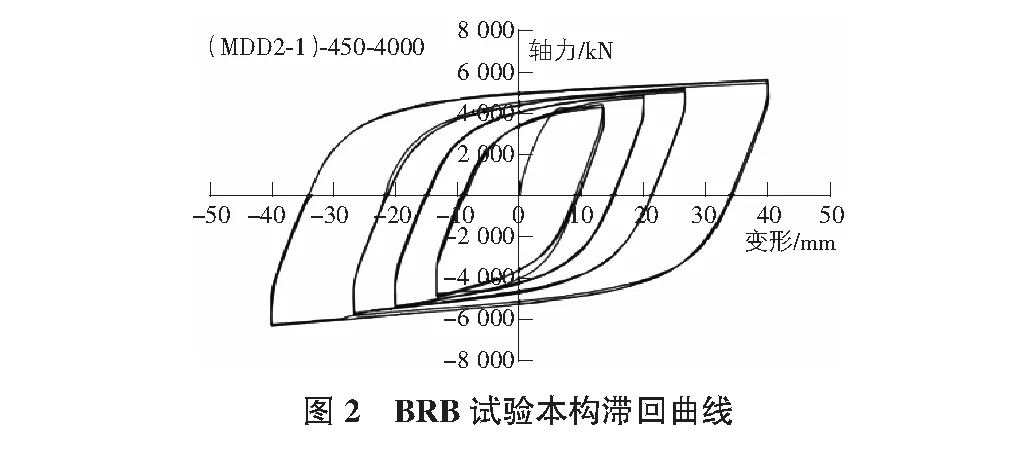
3 模拟分析

根据BRB资料建立模型，由于无粘结材料通常由弹模较小材料如橡胶、聚乙烯、硅胶等构成，模型中将其设置为厚度等同无粘结材料的空腔，两者接触关系为无摩擦。考虑内芯钢材厚度、外套筒厚度、无粘结材料厚度等因素的影响，将其设置为t1，t2，t3。据实t1=35 mm，t2=10 mm，t3=2 mm。钢套管钢材Q345，内芯钢材Q235，C30混凝土填充,见图3。

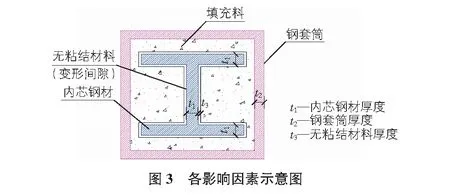
上述条件下BRB的计算结果见图4，此时滞回曲线较饱满，且最大拉、压力与试验数值接近，斜率接近，故计算可较好的模拟BRB静力拉压试验，模型合适。

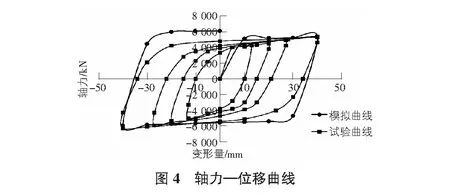
设置三个影响参数的变量为：内芯钢材厚度t1=(25/35) mm、外套筒厚度t2=(10/20) mm、无粘结材料厚度t3=(0.5/2) mm时，组合见表1。

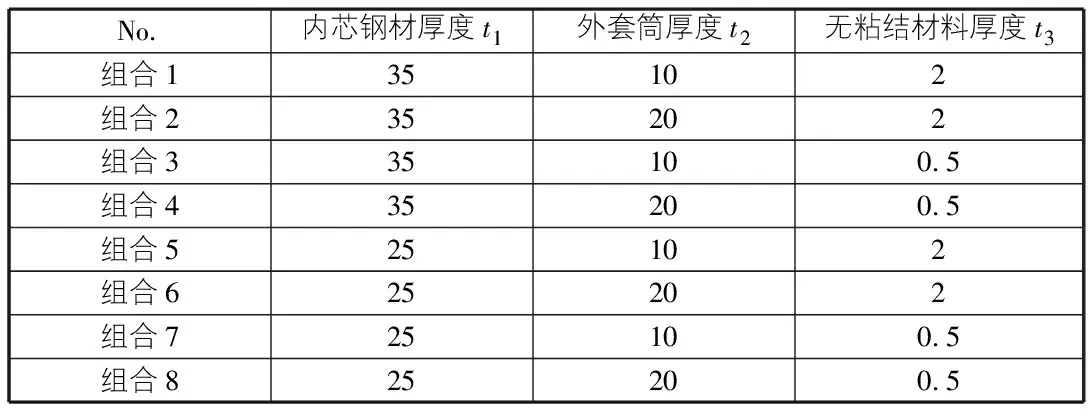
表1 各组合参数表

各组合结果与试验结果对比见图5，可见各组合下BRB均有良好滞回性，滞回曲线饱满。

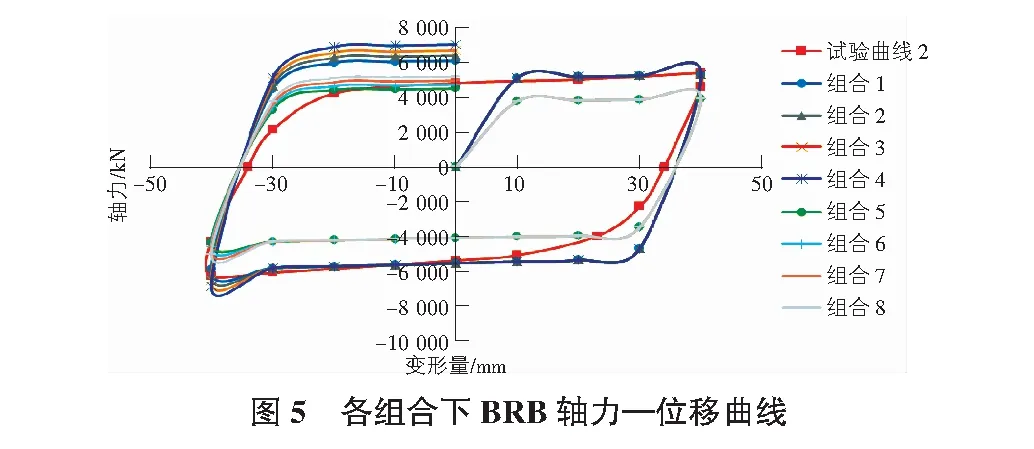
3.1 内芯钢材厚度t1的影响

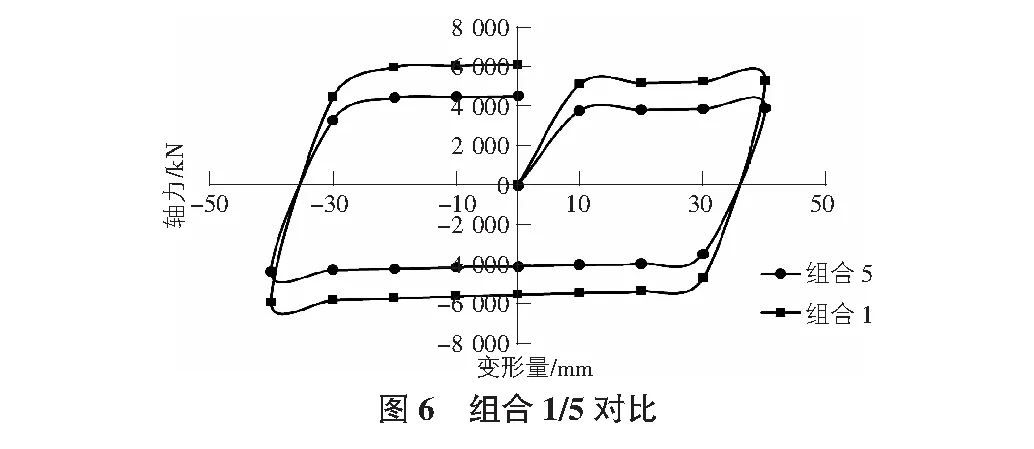
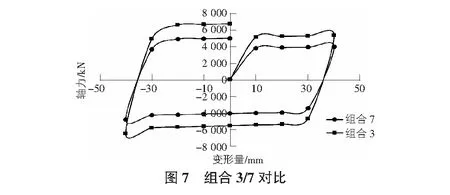
为对比内芯钢材厚度t1对BRB承载能力的影响，将以上组合1/5、组合3/7进行对比，如图6，图7所示。组合1中最大拉力、压力均高于组合5；组合3中最大拉力、压力均高于组合7。对比各组在弹性范围内斜率，组合1、组合3均分别高于组合5、组合7。可知，当内芯钢材厚度t1变大时，BRB最大承载拉压力均提高，两者正相关，且弹性范围内斜率也随之增大，即构件刚度增大。

3.2 外套筒厚度t2的影响

为对比外套筒厚度t2对BRB承载能力的影响，将组合3/4、组合7/8进行对比，如图8，图9所示。组合4中最大拉压力均高于组合3；组合8中最大拉压力均高于组合7。由此，当外套筒厚度t2变大时，BRB最大承载拉压力均提高，两者正相关。当外套筒厚度t2变大时，当构件变形为正，内芯钢材与填充料、外套筒未接触，对BRB承载力基本无影响；当构件变形为负，其对内部填充料的约束能力增强，并反映到填充料对内芯钢材的约束作用上，从而提高BRB承载力。

3.3 无粘结材料厚度t3的影响

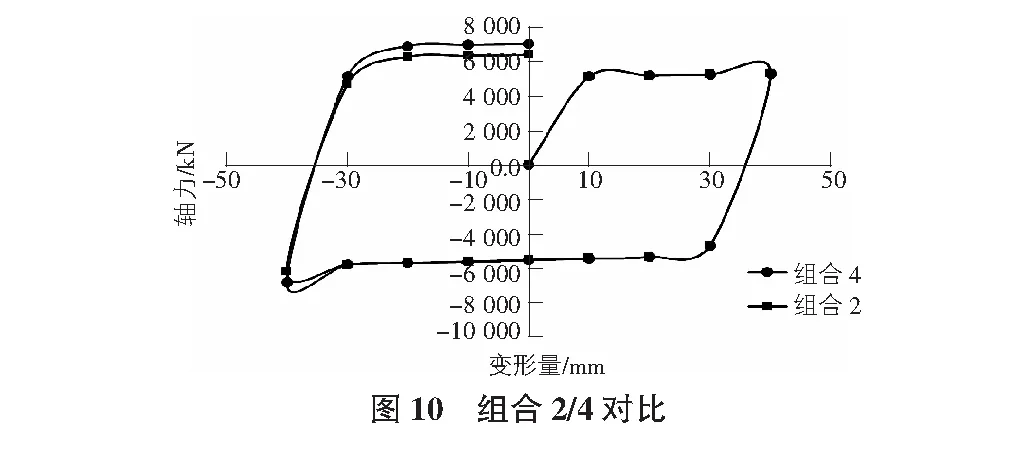
为对比无粘结材料厚度t3对BRB承载能力的影响，将组合2/4、组合6/8进行对比，如图10，图11所示。当无粘结材料厚度t3变大时，BRB最大承载拉压力都将降低，两者负相关。随着间隙的增大，当构件变形为正，内芯钢材与填充料、外套筒未接触，其对BRB承载力基本无影响；当构件变形为负，BRB内芯钢材的约束被降低，其受压变形时自由空间增大，失稳波幅也随之增大，支撑承载力与耗能能力随之降低。

4 结语

本文通过变换组合影响工字型BRB核心本构关系的三个因素，得到其对本构关系影响：当内芯钢材厚度变大时，BRB最大承载拉压力、弹性范围内的斜率都有提高，二者正相关。当外套筒厚度变大时，当构件变形为正，内芯钢材与填充料未接触，不影响BRB承载能力；当构件变形为负，其对内部填充料与对内芯钢材的约束能力增强，从而提高BRB的承载能力。当无粘结材料厚度变大时，当构件变形为正时，内芯钢材与填充料未接触，不影响BRB承载能力；当构件变形为负时，BRB内芯钢材的约束被降低，其受压变形时的失稳波幅也随之增大，支撑承载力与耗能能力随之降低。