电磁发射打击精度计算方法分析

唐晓燕，连海根，余俊松，杜 雪

（1.中国电子科技集团公司第二十七研究所，河南 郑州 450047；2.陆军装备部驻西安地区军事代表局驻郑州地区军事代表室，河南 郑州 450047）

武器系统的效能评估是武器研制过程中十分重要的一个问题。射击精度是衡量武器系统能否命中目标的一个重要战技指标，精确打击是现代兵器发展的最终追求目标。射击精度的估计与评定一直受到武器研制和鉴定部门的关注。射击精度包括射击准确度和射击密集度，前者描述了落点的系统性偏差，后者描述了落点的随机散布特性。

电磁轨道炮发射弹丸的速度突破了普通火炮的性能极限，弹丸具有重大的动能，大大增强了对目标的毁伤能力，同时减小了弹丸到达目标的飞行时间，增加了对付快速目标的有效性和命中率，电磁轨道炮视为未来防空作战中的重要备选武器之一，电磁轨道炮精确打击在电磁轨道炮研究领域具有非常重要的地位。

1 射向散布定义

在相同条件下，向同一目标发射出多枚射弹，由于多种因素的影响，射弹的弹着点将在目标附近形成散布，其平均弹着点（散布中心）到瞄准点（一般为目标中心）的距离称为炮弹的系统误差，每个弹着点到平均弹着点的距离称为随机误差，亦称散布度。通常系统误差比随机误差小并可以修正，因此又近似地把瞄准点作为平均弹着点。

电磁发射系统的系统误差主要包括发射系统集成装配误差、膛口抖动误差等。随机误差主要包括膛口抖动和电弧力作用误差等。

对于电磁轨道炮，系统误差可以通过标校进行修正，本文通过电磁轨道炮的打击精度重点考虑射击密集度情况，即射向散布情况。通过对不同的射向散布计算方法进行对比分析，寻找适合的射击精度评估方法。

2 射向散布计算方法

武器系统射击精度的估计方法有许多种，火炮、轻武器、地地战略导弹等武器系统常用圆概率误差CEP50的计算方法进行效能评估，本文根据CEP50的计算方法给出相应的CEP70、CEP80计算公式，同时提出最大包络法、高速射像质心法和图解法这三种新的射向散布计算方法，下面对上述不同散布评估方法进行介绍。

2.1 圆概率误差法

圆概率误差是衡量炮弹命中精度的一个尺度。计算圆概率误差的一般方法是先测出各弹着点的坐标，求出平均弹着点的坐标，再用数学公式进行计算。对立靶目标进行射击，以目标为中心，射击方位方向分为横轴，射击高低方向分为纵轴，以（Y，Z）表示立靶靶面弹丸落点坐标，且（Y，Z）服从正态分布，纵横向独立。

圆概率误差CEP：

式中：σz、σy表示方向、高低散布标准差；μy、μz表示方向、高低散布均值；ρ表示高低、方向落点偏差相关系数，0≤|ρ|<1；

（1）CEP50计算公式如下：

根据上述CEP50的计算过程，用同样地计算方法，给出CEP70，CEP80的圆概率误差计算公式。

（2）CEP70计算公式如下：

（3）CEP80计算公式如下：

射向散布：2CEP/L（全角），L为炮口到靶心距离。

2.2 最大包络法

根据一组试验射弹在靶板上的弹着点最大包络进行计算。

假设试验最大包络尺寸为Y*Z（Y方向为俯仰方向，Z方向为水平方向），弹长为D，炮口距离靶面垂直距离为S，η为射弹姿态有翻转的情况，着靶后扩大弹孔采取缩减系数，则下弹着点包络在俯仰和水平方向的射向散布分别是：

2.3 图解法

对于图解法，本文通过计算不同射弹落点与平均坐标点之间的距离，并将这些距离由小到大排序，这些距离可以看做是不同大小的半径，以平均坐标为圆心，可以绘制出若干不同的圆，这些圆包含射弹落点数依次为1，2，3……，n，（n表示为试验中发射的射弹量）。根据落点数量可计算不同圆对应的落点率，由此得到不同落点对应的射向散布精度。具体步骤如下：

（1）先测出各弹着点的坐标，（Yi，Zi）表示立靶靶面弹丸落点i（i=1、2、…、n）的俯仰、水平坐标。

（2）根据已测得弹着点坐标，计算出平均弹着点坐标，即散布中心

（3）计算各点的散布半径Ri。

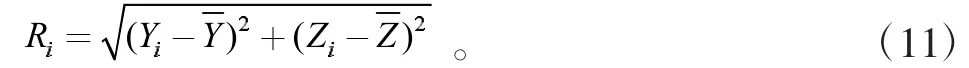
（4）对计算出的各点散布半径进行从小到大的排序，得到R'j，其中j=1、2、…、n。

（5）绘制包络圆，以散布中心（Y，Z）为圆心，排序后的各散布半径R'j（j=1、2、…、n），得到的圆命名为C（j）（j=1、2、…、n），包含的落点数量分别对应1、2、3，……，n。

（6）计算对应要求落点率的射向散布精度。

a.落点率：η=j/n。

b.不同落点率对应的射向散布精度：δ=2R'j/L。

3 不同计算方法结果对比分析

某电磁发射进行若干发次模拟发射试验，模拟试验前约定散布要求，按照上一章节射向散布计算方法进行计算绘图，结合落点率和散布要求进行方法对比分析。

（1）对于圆概率误差法，图1给出圆概率误差CEP50、CEP70、CEP80包含射弹点数。

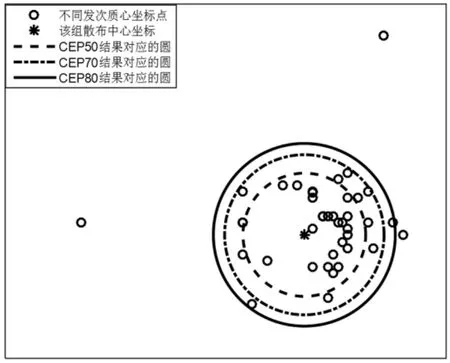
图1 圆概率误差法示意图

从图1中可看出：CEP50、CEP70、CEP80这三种圆概率误差法通过计算公式绘图的实际落点率要远远高于计算公式对应的落点率，这是由于圆概率误差计算方法适用于试验数据较大情形，在试验数据较小的情况下圆概率误差方法将不适用。

（2）对于图解法，根据不同落点率要求进行画圆，获取足够数量的落点以满足不同落点率要求。图2给出采用图解法绘制的圆图，不同的圆包含不同的射弹落点情况。

图2 图解法画圆示意图

从图2中可看出不同圆中的落点率与实际要求完全一致。

（3）对于最大包络法，可以快速计算出射向散布结果，且包含全数落点，但考虑全数落点会致使射向散布偏大，不满足要求，对此可以缩小包络，采用满足散布要求的方框进行替代，在此方框内计算相应落点率，检测在射向散布要求下是否满足落点率要求。

从图3中可以得到，在不进行全数落点统计的情况下，进行满足散布要求的最大包络绘制，并进行落点率统计，得出既满足散布要求，又不低于落点率要求的最优包络。

图3 最大包络示意图

按照射向散布要求，可以将靶面绘制成圆形，也可绘制成方框形状，图4给出按照散布要求绘制的图形。

从图4中可得出以下结果：

图4 散布要求示意图

a.圆形和方框包络对应的落点率不同，方框落点率要优于圆形落点率。

b.由于方框包络面积大于圆形包络，在满足射向散布要求前提下，落点率情况方框优于圆形。

4 结论

四种射向散布计算分析方法，都可以有效获得射向散布结果，不同的计算方法对指标满足度有一定的影响。

（1）由于受到电磁动能武器寿命限制，受到试验数据量的影响，圆概率误差法在计算落点率结果上存在较大偏差，实际落点情况优于计算公式对应的落点率。

（2）图解法可以有效解决圆概率误差方法中存在的落点率不一致问题。

（3）最大包络法可以有效计算出所有落点情况下的射向散布结果，在全数落点情况下，射向散布结果可能出现超出要求情况，对此收缩小包络，采用满足散布要求的方框进行替代，在此方框内计算相应落点率，检测在射向散布要求下是否满足落点率要求。