一种优化的对流层天顶延迟融合模型FZTD

全雪贞，张洁，宋秀容，杨彬

(1.青海省基础测绘院，西宁 810001；2.湖南大学电气与信息工程学院，长沙 410082)

0 引 言

当电磁波穿过大气层时会产生折射延迟，按照折射介质的不同，主要分为电离层延迟和对流层延迟.其中电离层延迟可以利用双频观测进行校正，但对于对流层延迟这一方法并不适用.在天顶方向对流层延迟约为2 m，而在低卫星高度角的情况下延迟值则会增加到几十米，因此对流层延迟是影响空间大地测量精度的主要因素之一.

通过建立对流层天顶延迟融合模型(FZTD)进行延迟改正是目前减弱这一影响的主要方法.而其中盲模型法由于其无需实测气象参数的输入被广泛应用于实时的GNSS 导航定位中.早期的盲模型则是以UNB 系列模型为代表[1-2]，Collins 等[1]首先于1996 年等提出了UNB1 模型，该模型将气象参数假设为常量，并未考虑空间位置和时间变化的影响，其精度较差为dm 级.随后引入纬度的变化影响，建立了UNB2 模型，但仍未考虑气象参数随时间变化的影响.1998 年，作者基于美国标准大气(1996)提出了UNB3 模型，其中气象参数的时间变化参考Niell 映射函数的表达方式，并以表格的方式表示不同纬度的气象参数.之后又考虑到直接采用水汽压参数所导致的相对湿度异常问题，将气象参数表格中的水汽压替换为相对湿度，建立了UNB3m 模型，其全球改正精度约为5 cm.UNB3 系列模型简单易用，是目前应用最为广泛的模型之一，但由于其假设气象参数南北半球对称，导致其在南半球的精度明显低于北半球.到2000 年后，随着大气数值模式的发展，涌现了许多基于数值模拟再分析资料的对流层延迟盲模型，主要有：TropGrid 系列模型[3-4]、GPT 系列模型[5-8]、IGGtrop系列模型[9-10]以及全球天顶对流层延迟(GZTD)模型[11-12].由于气象参数时空分辨率的提高，使得这些模型的精度提高到了4 cm 左右，但这也直接导致了气象参数的急剧增加.目前标称精度最高的模型为GPT2w 模型，可达3.6 cm.因此GPT 系列模型也是目前对流层研究领域最为关注的模型.2007 年Bohm[5]等利用ECMWF 资料基于球谐函数提出了面向大地测量应用的GPT1 模型，该模型仅包含全球气压和温度参数.之后Lagler 等[6]对GPT1 模型进行了改进提出了GPT2 模型，模型不仅增加了比湿、温度递减率和干湿映射参数，而且引入了气象参数的半年变化周期，空间分辨率为5°×5°.Bohm[7]等则在GPT2 模型的基础上，通过引入新的湿延迟模型，并增加水汽压递减率和加权平均温度两个参数，提出了GPT2w 模型，其空间分辨率可达1°×1°，全球精度为3.6 cm，目前最新的GPT 系列模型版本为GPT3[8].虽然时空分辨率以及气象参数的增加提高了GPT 系列模型的精度，但也使得模型参数的总量急剧增加到了270 多万个.这限制了该系列模型在内存占用要求较小的GNSS 终端上的应用.

针对上述问题，本文结合UNB3 与GPT2w 模型各自的优势，提出了一种融合UNB3 与GPT2w 模型的简易且精度较高的FZTD.并利用多年的国际GNSS 服务(IGS)天顶对流层延迟(ZTD)数据对该模型的精度进行了验证，结果表明FZTD 模型在精度上优于传统UNB3m 和EGNOS 模型，在气象参数数量上比GPT2w 模型急剧减少，与传统模型相当，可作为GNSS 接收机中预定义的对流层延迟模型.

1 FZTD 模型的构建

考虑到UNB3 模型表达的简易性以及GPT2w模型参数的精确性，本文首先分析在ZTD 模型的基础上，从GPT2w 模型中提取基础模型所需的气象参数，然后通过分析气象参数的空间分布特征，按照UNB3 模型的表达方式建立新模型的气象参数查询表，最后完成FZTD 模型的构建.

1.1 ZTD 基础模型

ZTD 可分为干延迟(ZHD)和湿延迟(ZWD)两个部分，其中干延迟计算的采用Saastamoinen 公式[13]

式中：P0为平均海水面处的大气压；H为测站海拔高度；φ 为测站纬度；T0为海平面处温度；Rd=287.054 J·(kg·K)−1为干气气体常数；gm=9.806 65 m/s2为平均重力加速度；β 为温度递减率.

ZWD 计算则采用Askne & Nordius 公式[14]

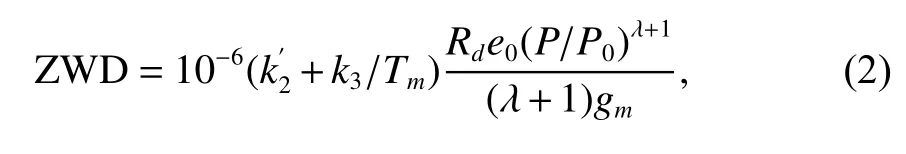
1.2 气象参数的空间特征分析与建模

根据以上对流层基础模型可以看到，模型计算所需的气象参数主要包括P0、T0、e0、β、λ 以 及Tm等6 个参数.本文首先利用GPT2w 模型计算得到以上6 个参数在1°×1°网格上5 年的时间序列.考虑到所建模型的简易性，我们仅考虑气象参数的年变化规律，因此我们需要对上述获取的气象参数时间序列做进一步的拟合处理，具体拟合公式如下：

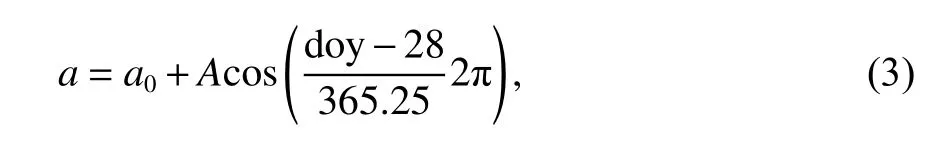
式中：a为气象参数；a0为气象参数的年均值；A为年变化振幅；doy 为年积日.

经拟合后可得到上述6 个气象参数在全球1°×1°网格上的年均值以及振幅，在此基础上对气象参数的空间分布特征进行分析.从大量的前人研究结果可以知道对流层延迟及其相关气象参数与纬度分布密切相关，同时考虑到大气压和水汽压分别是ZHD和ZWD 模型中的主要影响因子，因此我们依据大气压和水汽压在纬度上的变化特征，对气象参数的空间变化进行线性划分.首先我们获取同一纬度带不同经度的大气压和水汽压年均值的平均值，然后依据它们随纬度的变化规律，提取变化的特征点，在此基础上对各气象参数进行分段线性建模.

图1 为大气压和水汽压经向均值随纬度的变化情况.水汽压呈现较为明显的南北对称，但大气压明显呈现非南北对称，特别是在南纬65°附近出现了984 hPa 的最低值，比之北纬65°处的1 013 hPa 两者相差29 hPa.可见UNB3 模型中假设气象参数均为南北对称并不符合真实的大气压分布规律.因此，我们通过提取以上两个参数随纬度的变化特征点，同时采用分段线性函数进行建模，在纬度方向上对气象参数进行了划分，共分为：[−90,−65]、[−65,−30]、[−30,−5]、[−5,5]、[5 ,15]、[15,35]、[35,60]、[60,80]以及[80,90] 9 个线性区间.表1 和表2 分别为各分段点的气象参数值年均值和振幅.

图1 大气压和水汽压的纬度分布及其变化特征点提取

表1 FZTD 模型气象参数年均值

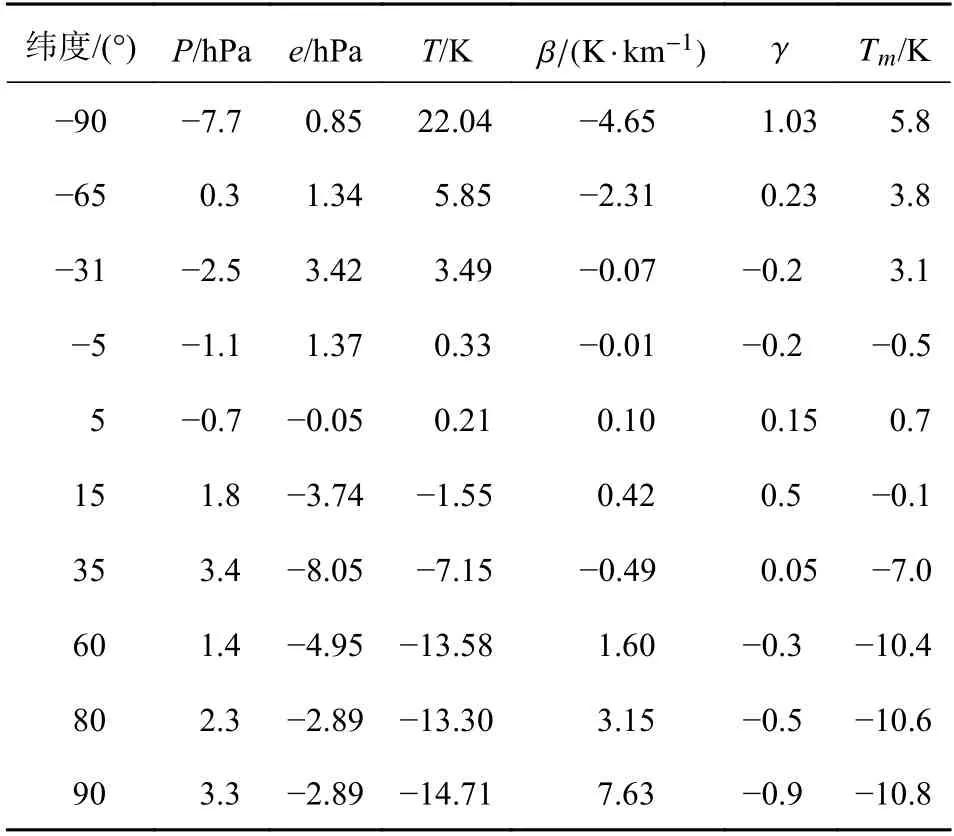
表2 FZTD 模型气象参数振幅

1.3 气象参数的计算方法

利用FZTD 模型计算对流层天顶延迟首先需要获得各气象参数值，依据表1 和表2 的气象参数年均值和振幅，任意测站各气象参数经验模型系数可由式(4)计算得到：

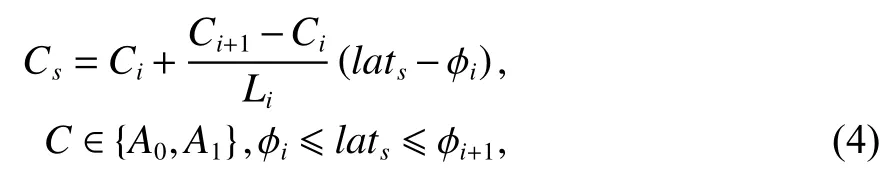
式中：Cs为测站气象模型系数；Ci为φi处的系数值，具体值从年均值A0集合和振幅A1集合中获取；Li=φi+1−φi为测站所在区间长度；lats为测站纬度.然后将计算得到的气象模型系数代入到气象参数的年周期模型中，即可得到该测站处任意时刻的气象参数值.具体计算方法如下：

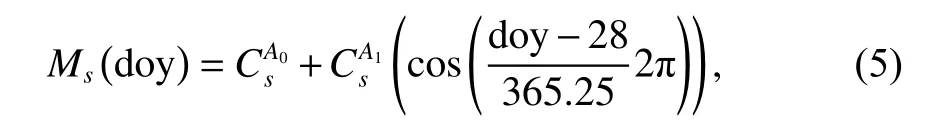
式中：Ms为测站气象参数；doy 为年积日；为年均值；为振幅.利用公式即可计算得到p0、T0、e0、β、λ、Tm6 个气象参数值.最后将计算得到的气象参数，作为式(1)和式(2)的输入参数，可分别计算得到ZHD和ZWD，两者之和即为总天顶对流层延迟值ZTD.

2 FZTD 模型精度评价

为了验证FZTD 模型的精度，我们利用全球367 个国际GNSS 服务(IGS)站点2011—2015 年的ZTD 数据作为参考值对FZTD 模型的全球适应性进行了评价，并与UNB3m、EGNOS 以及GPT2w 模型进行了对比.表3 为各模型在全球范围内的均方根(RMS)和平均偏差(bias)，从表3 可以看到，FZTD 模型在全球范围内的RMS 值为4.4 cm 比UNB3m 和EGNOS 模型的RMS 5.1 cm 提高了0.7 cm，精度提升较为明显，而且其bias 为−0.3 cm，说明该模型存在低估ZTD 的现象.FZTD 模型的bias 绝对值与EGNOS相当，但比UNB3m 模型的bias 1.1 cm 提高了0.8 cm.当然相比于GPT2w 模型，FZTD 模型在RMS 和bias绝对值两个方面均较大，这主要是由于FZTD 模型的输入气象参数是源于对GPT2w 模型数据的简化，仅考虑了参数的纬度和年变化，而GPT2w 模型不仅空间分辨率可达1°×1°，而且更是考虑了气象参数的半年变化.但FZTD 模型的参数数量仅为120 个，比之GPT2w 模型的270 多万个，所需存储空间急剧减少，更适用于嵌入式GNSS 的实时导航定位应用.

表3 FZTD、UNB3m、EGNOS 和GPT2w 模型的误差统计 cm

图2 和图3 分别示出了FZTD、UNB3m、EGNOS和GPT2w 四个模型RMS 和bias 值的全球分布情况，我们可以看到，FZTD 模型呈现在热带地区多为低估，其他地区多为高估的现象，较大bias 值多出现在海陆交界处.由于采用了相同的气象参数查询表，UNB3m 与EGNOS 模型的全球分布较为相似，在南半球的高估现象异常明显，别特是在南极地区最大偏差可达11.4 cm.这主要是由于气象参数南北对称的假设所导致的.GPT2w 模型的bias 值在全球范围内变化较为平缓，且多数值接近于0，在所有模型中表现最佳.在RMS 值方面，FZTD 模型整体呈现从赤道向两极递减的趋势，而UNB3m 与EGNOS 两模型则呈现从北极向南极波动的变化趋势，在南极地区RMS 值达到最大.GPT2w 模型的RMS 值在全球范围分布较为一致，其较大值多出现东南亚地区，这说明在该地区GPT2w 模型还需进一步细化.

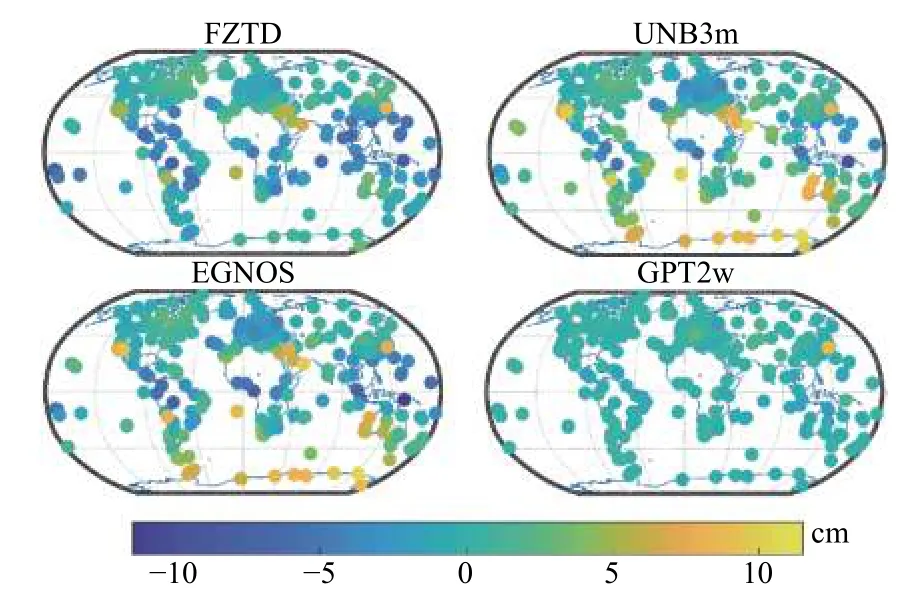
图2 FZTD、UNB3m、EGNOS 以及GPT2w 模型bias 值的全球分布

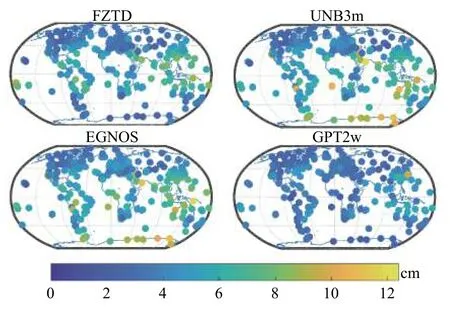
图3 FZTD、UNB3m、EGNOS 以及GPT2w 模型RMS 值的全球分布

为了进一步验证FZTD 模型的改正效果，我们统计分析了不同纬度带各模型的RMS 与bias 值，具体分析结果可如表4 所示.从表中可以看到FZTD 模型精度在北半球高纬度地区略低于UNB3m 模型，但高于EGNOS 模型.而在赤道附近FZTD 模型与UNB3m模型精度相当，但高于EGNOS 模型.在北纬15°～60°以及南纬30°～90°地区，FZTD 模型比之UNB3m与EGNOS 模型有较为明显地提高，特别是的南极地区精度更是提高了3 倍多，且精度与GPT2w 模型相当，这说明FZTD 模型更适合于在南极地区的应用.

表4 FZTD、UNB3m、EGNOS 以及GPT2w 模型在不同纬度带下的RMS 与bias 统计 cm

3 结 论

本文基于UNB3 模型中以查询表方式描述全球气象参数分布规律的思想，对GPT2w 模型参数进行了简化，构建了FZTD 模型.并通过IGS 站提供的ZTD 数据对FZTD 模型在全球范围内的适用性进行了评价，结果表明，该模型的全球改正精度优于传统UNB3m 和EGNOS 模型.特别是在南半球区域精度改善尤为明显，在南极地区提高了近70%.虽然该模型整体精度不如GPT2w 模型，但其所需气象参数少和UNB3m 和EGNOS 模型处于一个量级，在GNSS实时导航定位领域具有更为广阔的应用前景，可以作为一种预定义对流层延迟模型嵌入到GNSS 接收机中.