改进Sage-Husa 算法在飞机组合导航中的应用
孙淑光,温启新
(中国民航大学 电子信息与自动化学院,天津 300300)
0 引 言
全球卫星导航定位技术在航空领域中的应用日益广泛.以美国的全球定位系统(GPS)、俄罗斯的格洛纳斯系统(GLONASS)、欧盟的伽利略系统(Galileo)和中国的北斗卫星导航系统(BDS)为典型代表,共同组成了全球卫星导航系统(GNSS)[1].GNSS具有全天候、导航定位精度高等优点,但其信号易受遮蔽与干扰,对精确导航定位产生影响.机载惯性导航技术具有完全自主、无源性、实时性强,输出参数全面等优点,已成为现代民航飞机、军用飞机航电系统的重要组成部分,但其也有导航误差随时间快速发散、初始对准时间长等缺点[2].捷联惯性导航系统(SINS)具有结构简单、重量轻、可靠性高等优点,是目前最常使用的惯性导航系统.GNSS/SINS 组合导航系统结合二者的优点,使组合后系统定位精度、连续性及有效性优于单系统工作状态[3-4].
GNSS/SINS 组合导航系统一般采用卡尔曼滤波来实现[5].传统卡尔曼滤波需通过建立精确的系统模型与噪声模型来保持良好的滤波精度,但在实际应用中系统状态与干扰噪声统计特性难以预先进行准确判断和建模[6],会出现滤波精度低甚至滤波发散等情况.为解决上述问题,文献[7]应用了传统Sage-Husa自适应滤波算法,但算法计算量大,实际应用中难以满足滤波实时性的要求.文献[8]和文献[9]中对传统Sage-Husa 自适应滤波算法进行简化,并对系统量测噪声进行优化处理,提高了滤波的准确性,但算法并未考虑滤波异常的情况,使其无法在滤波出现异常情况时做出及时调整.文献[10]结合滤波异常判据的条件,对Sage-Husa 自适应滤波算法进行改进,使其适用于特定的系统工作环境,提高了滤波精度.
针对飞机全飞行过程,本文提出一种改进的Sage-Husa算法,引入飞机气压高度作为滤波异常判断条件,结合GNSS/SINS 组合导航,提高定位精度,增强组合导航滤波算法自适应性.
1 GNSS/SINS 组合导航系统模型
GNSS/SINS 组合导航系统整体架构如图1 所示.其中GNSS 接收机通过接收导航卫星信号,解算出用户的位置与速度,SINS 通过惯性测量元件测量出用户的比力与角速度,经过惯性导航解算得到用户位置与速度.最后将上述两种导航系统求得用户位置与速度通过组合导航系统进行数据融合,并利用融合后的数据进行SINS 误差补偿,最终得到最优导航输出信息.
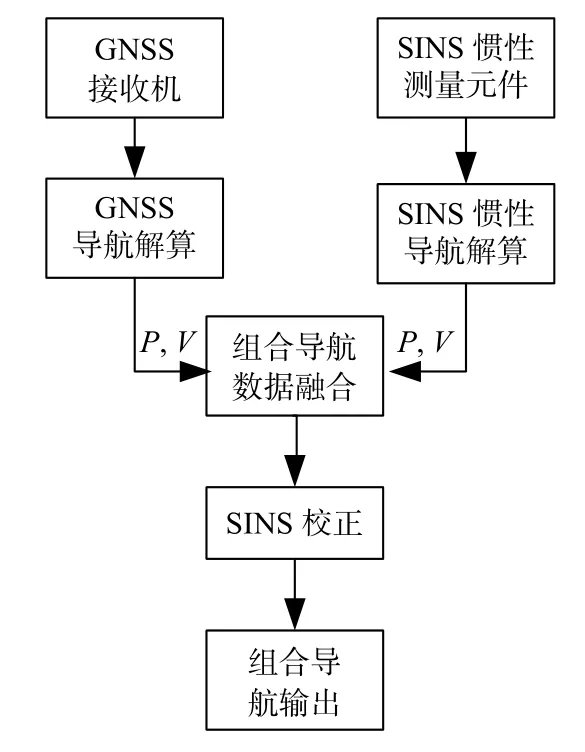
图1 GNSS/SINS 组合导航架构图
1.1 GNSS/SINS 组合导航系统状态方程
GNSS/SINS 组合导航系统中,选取的状态变量包括经度误差 δLI、纬度误差δ λI、高度误差δhI、东(E)、北(N)、天(U)坐标系下的E 方向速度误差 δvIe、N 方向速度误差 δvIn、U 方向速度误差 δvIu、E 方向姿态角误差 δφe、N 方向姿态角误差 δφn、U 方向姿态角误差 δφu、机体坐标系下三个坐标轴方向的陀螺仪漂移误差 εx、εy、εz以及加速度计漂移误差∇x、∇y、∇z.状态变量的微分方程如下:


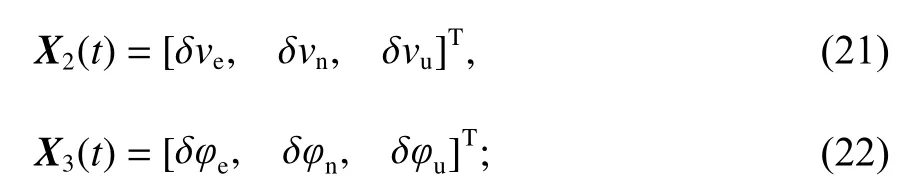
G(t) 表达式为

W(t) 表达式为
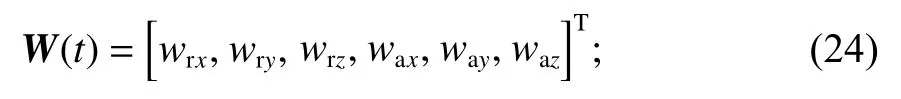
F(t) 为系统状态转移矩阵,表达式为
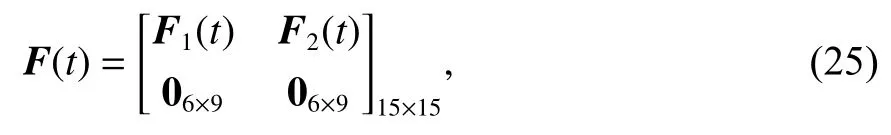
矩阵F1(t) 各元素可由系统状态变量的微分方程推导出,F2(t) 表达式为
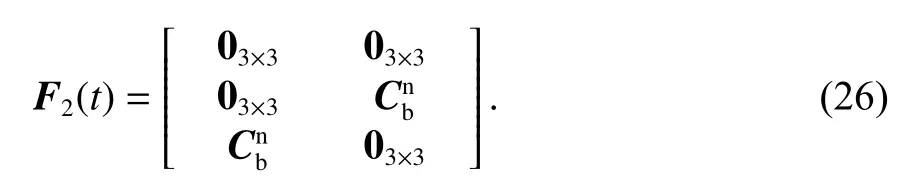
1.2 GNSS/SINS 组合导航系统量测方程
GNSS/SINS 组合导航系统采用松组合方式,故将GNSS 解算的位置和速度与SINS 测量得到的位置和速度之差,作为组合导航系统量测信息.将飞机在导航坐标系下的真实位置设为(L,λ,h),真实速度设为(ve,vn,vu),SINS 解 算的位置与速度可分别为(LI,λI,hI)、(vIe,vIn,vIu).GNSS 解算的位置与速度可分别为(LG,λG,hG)、(vGe,vGn,vGu),可得GNSS/SINS 组合导航系统量测方程为
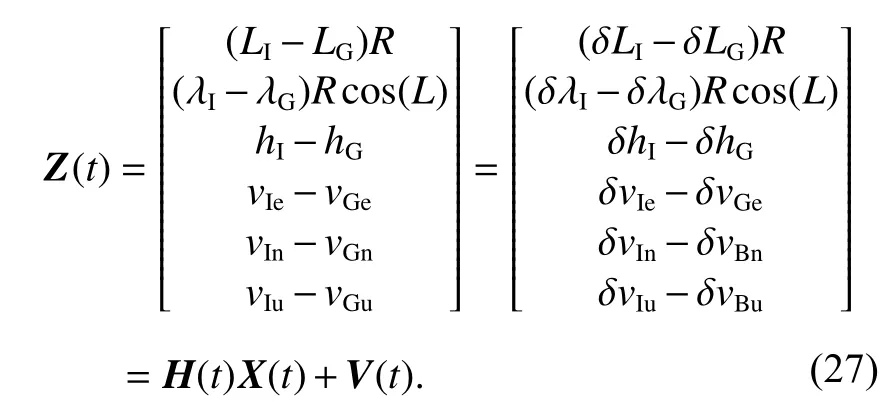
式中:H(t) 为
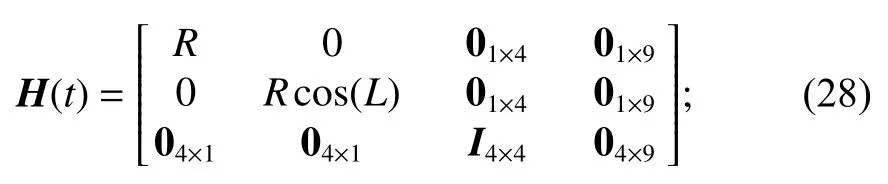
量测噪声矩阵V(t) 为

将式(18)与式(27)进行离散化,可得GNSS/SINS组合导航离散时间的系统模型为
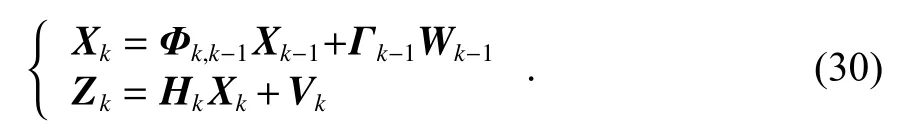
式中:Φk,k−1为离散化后的系 统状态一步转移 矩阵;Γk−1为离散系统噪声分配矩阵;Wk−1为系统噪声矩阵;Hk为离散系统量测转移矩阵;Vk为量测噪声矩阵.
2 改进的Sage-Husa 自适应滤波算法
2.1 Sage-Husa 自适应滤波算法特性分析
针对离散化后的GNSS/SINS 组合导航系统模型,其系统噪声Wk−1与 量测噪声Vk满足以下统计特性 :E (Wk)=qk,D (Wk)=Qk,E (Vk)=rk,D (Vk)=Rk且.即系统噪声Wk的均值为qk,方 差为Qk,系统量测噪声Vk的均值为rk,方差为Rk,且两者相互独立.传统卡尔曼滤波算法中,要求系统噪声Wk−1与 量测噪声Vk均为均值是零的高斯白噪声(WGN),针对噪声对象单一,实际应用中噪声类型复杂,噪声统计特性难以判断,卡尔曼滤波算法难以获得系统状态最优估计.
Sage-Husa 算法对系统状态进行最优估计过程中,对系统噪声Wk−1与 量测噪声Vk的均值与方差进行实时估计与校正,确保系统滤波处于正常状态.然而在飞机实际飞行过程中,当其飞行环境平稳,系统滤波正常时,无需对系统噪声的统计特性进行校正,因此文献[11]中引入滤波异常的判据条件:
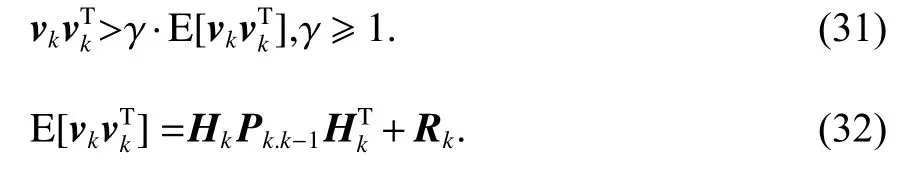
式中:γ 为调节因子,表示滤波异常判断的严格程度;vk表示量测新息序列,表示新息序列方差的理论预计值.当式(31)成立时,说明新息序列的实际方差大于理论预计值的 γ 倍,系统滤波出现异常,需对量测噪声做出调整,保证系统正常滤波.
2.2 改进的Sage-Husa 自适应滤波算法
民用航空飞机的飞行阶段可划分为:起飞、爬升、巡航、进近、着陆阶段,其中起飞和着陆时间约占飞机总飞行时间的6%,但是却有近一半的飞行事故发生在该阶段[12].另外,飞机的起飞和着陆阶段,相比于爬升与巡航阶段,距离地面高度较低,导航定位精度对飞行安全的影响增大.
因此,当飞机飞行高度越低时,组合导航系统滤波结果要求更加精确,保证飞行所需的定位精度.通常情况下,在WN 模型已知的前提下,卡尔曼滤波输出为最优线性无偏估计,但是在复杂的飞行环境中,飞机受到的干扰噪声(如:空间中的电子干扰,机场终端区由于多路径效应产生的反射叠加噪声等)并不能全面提前预测,对于未知噪声建立精确数学模型并掌握其数理统计特性是非常困难的.当飞机实际飞行所受到的干扰噪声与提前建立的卡尔曼滤波算法中的噪声模型不匹配甚至相差特别大时,卡尔曼滤波输出将会出现跳变、发散等滤波异常情况.
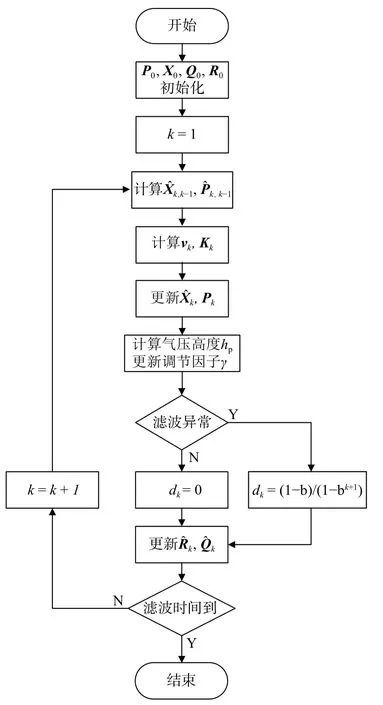
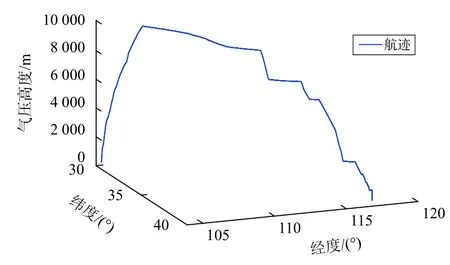
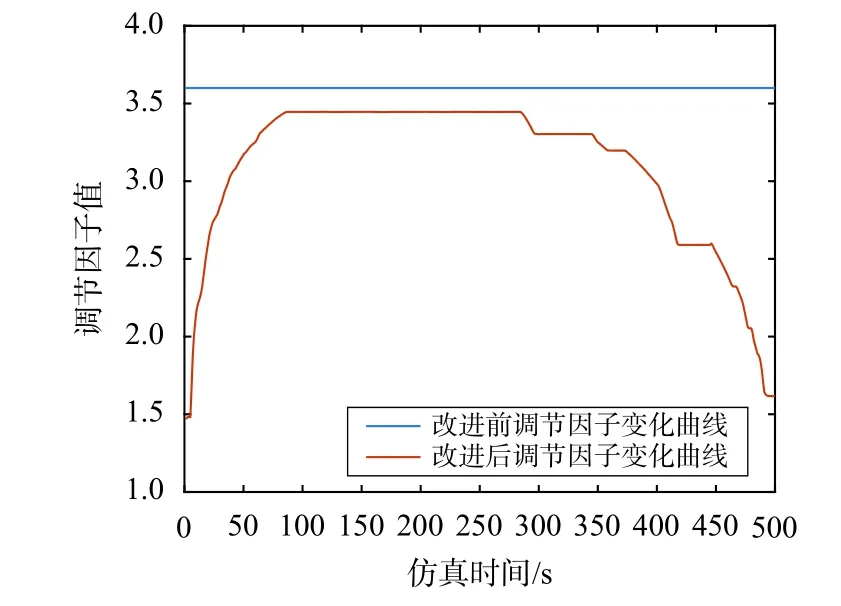
为满足飞机在不同飞行阶段中GNSS/SINS 组合导航系统滤波的精确性与自适应性,本文利用飞机气压高度hp,对Sage-Husa 自适应滤波算法进行改进.飞机在巡航阶段,气压高度的参考基准面为国际标准气压海平面(101.325 kPa),而当飞机进入机场管制区域时,气压高度的参考基准面为当地修正海平面[13],在特定飞行阶段中,气压高度的参考基准面具有确定性与统一性.因此,引入气压高度来对式(31)中的调节因子 γ进行优化,令

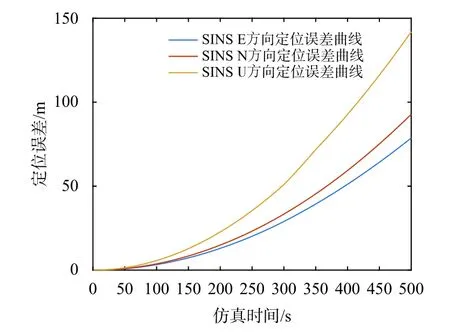
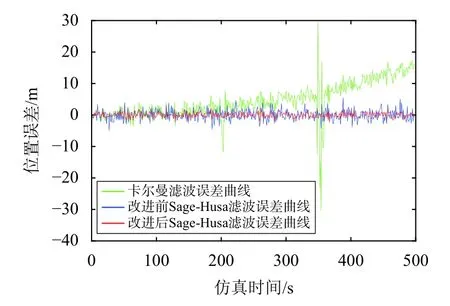
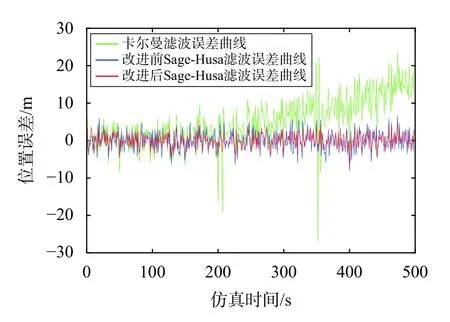
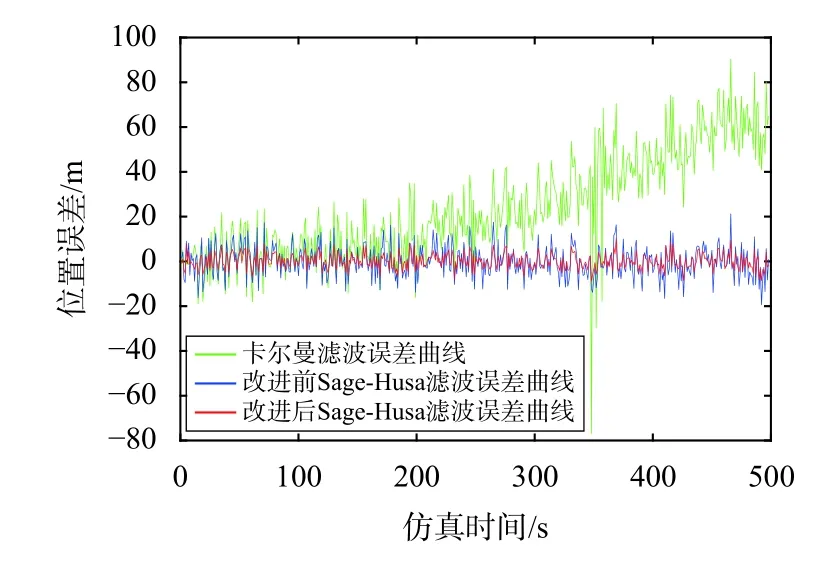
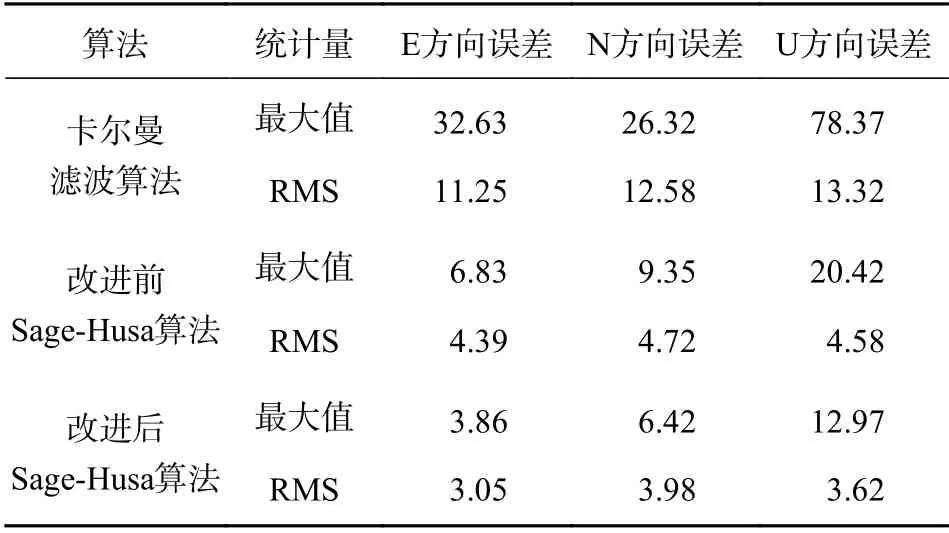
式中:B为大于0 的常数,a与C也为常数,a的取值范围为1 其中,b称为遗忘因子,一般在0.95~0.99 选取,调节因子 γ=Blogahp+C.改进后的自适应滤波算法,滤波异常判断严格程度随着气压高度的变化而变化.当飞机气压高度变低时,调节因子 γ 随之变低,系统滤波异常判断严格程度变高[14],当其气压高度变高,飞机在相应飞行高度层间隔增大,可进行调节飞行状态的空间与时间比在起飞与着陆阶段更加充足,此时调节因子 γ 增大,系统滤波异常判断严格程度降低,由此来增强飞机在不同飞机阶段组合导航系统滤波的自适应性.改进后的Sage-Husa 自适应滤波算法流程如图2 所示 图2 改进后的Sage-Husa 自适应算法流程图 本文利用从我国西南某城市到北方某城市真实机载快速数据记录器(QAR)的数据对改进后Sage-Husa 自适应滤波算法有效性进行验证.验证平台包含多个仿真模块:SINS 模块、GNSS 模块、组合导航滤波模块.QAR 数据可提供飞机位置、气压高度等信息,SINS 模块提供惯性元件测量的角速度、比力信息以及惯导系统解算的、位置信息,GNSS 模块提供导航卫星系统解算的用户速度与位置信息,组合导航滤波模块对两种导航信息进行数据融合,输出组合导航数据信息. 系统仿真时间为500 s,滤波频率为1 Hz;陀螺仪误差为均值为0 °/h,方差为0.03 °/h 的WGN;加速度计误差为均值为0 g,方差为1×10−5g 的WGN;GNSS 测量伪距误差为均值为10 m,方差为5 m 的WGN.SINS 输出频率为20 Hz,GNSS 输出频率为1 Hz.在200~210 s 内与350~360 s 内使其量测噪声扩大到原来的5 倍与10 倍,用来模拟实际飞行环境中飞机受到噪声干扰及量测噪声发生突变的情况. 利用真实QAR 数据获取验证用飞行轨迹,如图3所示,初始位置为北纬30.56°,东经103.94°,气压高度为489.51 m. 图3 飞机实际飞行轨迹 在本文仿真条件下,SINS 与GNSS 在导航坐标系下的定位误差如图4、图5 所示. 图4 SINS 定位误差 图5 GNSS 定位误差 由图4 可知,SINS 定位误差随着时间增长迅速积累,在东(E)、北(N)、天(U)三个方向都存在不同程度发散,其中在系统仿真时间结束时,E 方向定位误差发散到77.50 m,N 方向定位误差发散到91.68 m,U 方向定位误差发散到140.92 m.由图5 可知,在本文条件下GNSS 水平方向定位精度要优于垂直方向的定位精度,其中东向定位误差范围为−20.40~24.33 m,N 方向定位误差范围为−24.01~25.59 m,U 方向定位误差范围为−33.21~31.59 m.通过仿真结果可以看出,SINS 定位误差随着时间的积累而发散,故不适合长时间依靠该系统进行定位,GNSS 定位误差虽不会出现发散现象,但当可见星数量减少或出现导航信号受到遮蔽、干扰时,GNSS 定位误差也会出现增大的现象.因此不管是SINS 还是GNSS,其单系统定位精度都不能满足飞机飞行时定位精度要求,故需对不同导航方式进行组合,来提高飞机导航定位精度. 改进Sage-Husa 自适应滤波算法的遗忘因子选取b=0.98,调节因子 γ 为 图6 为改进前后的调节因子变化曲线对比图.通过引入QAR 中气压高度数据,对调节因子进行改进.从改进后的曲线可以看出,飞机起飞(0~50 s)、进近着陆(420~500 s)阶段调节因子数值偏小,此时滤波异常判断标准严格程度高.飞机在航路阶段(51~419 s)时,调节因子数值偏大,滤波异常判断标准严格程度变低,符合高空飞机之间间距要求较大的预期.根据气压高度调整滤波异常判断标准的严格程度,在确保飞行安全的前提下,提高了算法的自适应性.而改进前的调节因子为常值,难以根据气压高度的变化对系统滤波异常判断标准的严格程度进行动态调整. 图6 调节因子变化曲线图 在前述仿真条件下,分别进行卡尔曼滤波组合计算、改进前Sage-Husa 自适应滤波算法、改进后Sage-Husa 自适应滤波算法的组合导航解算的仿真,定位误差的仿真结果如图7~图9 所示. 图7 E 方向定位误差 图8 N 方向定位误差 图9 U 方向定位误差 由图7、图8、图9 以及表1 可知,在文中仿真条件下,在200~210 s 与350~360 s 时间段内增大量测噪声后,卡尔曼滤波算法在E、N、U 方向定位误差发生明显跳变,最大值分别为32.63 m、26.32 m、78.37 m,误差的均方根(RMS)值分别为11.25 m、12.58 m、13.32 m,且误差值随时间增长呈发散趋势,定位精度较低且误差波动范围较大,难以满足飞机起降阶段高精度定位的要求.改进前Sage-Husa 自适应滤波算法在E、N、U 三个方向的定位误差最大值分别为6.83 m、9.35 m、20.42 m,误差的RMS 值下降到4.39 m、4.72 m、4.58 m,提高系统定位精度的同时,减小了误差波动范围.改进后的Sage-Husa 自适应滤波算法在E、N、U 三个方向定位误差最大值分别为3.86 m、6.42 m、12.97 m,误差的RMS 值分别为3.05 m、3.98 m、3.62 m.可以看出,Sage-Husa 自适应滤波算法在量测噪声发生突变时,仍能使系统保持良好的滤波输出,且对误差发散现象起到良好的抑制效果.改进后的算法不仅降低了定位误差,使误差波动更加平滑,提高了定位精度,且随着飞行气压高度变化,借助调节因子的改变,使其适用于复杂的飞行环境与不同飞行阶段,增强了组合导航算法自适应性,可以更好地确保飞机安全平稳飞行. 表1 导航系下定位误差比较 m 本文针对飞机起飞、爬升、巡航、进近、着陆不同飞行阶段,利用气压高度对Sage-Husa 自适应滤波算法进行改进,同时对SINS 与GNSS 单系统的工作以及通过传统卡尔曼滤波算法进行组合导航工作时的定位误差特性进行仿真与结果分析,可获得以下结论: 1) SINS 定位误差随时间而积累,长时间工作会导致其误差发散严重,定位精度随系统时间增加严重降低.利用GNSS 定位时,其定位误差波动较大且导航信号易受遮蔽与干扰,不适用于在复杂电磁环境中工作,定位精度易受影响; 2) 卡尔曼滤波将SINS 与GNSS 进行组合导航,在一定程度上能够提高定位精度,但传统卡尔曼滤波算法对系统过程噪声与量测噪声的统计特性规定较严格,在实际复杂噪声环境应用中存在局限性,难以保证飞机在受到干扰时,仍保持良好滤波效果; 3) 利用气压高度对Sage-Husa 自适应滤波算法进行改进,将判断滤波异常严格程度的调节因子从原来固定不变的常数,转变为结合飞机实际飞行气压高度的动态变化值,以此来满足飞机不同飞行阶段对滤波标准的不同要求,效果良好. 在本文的仿真条件下,相比于改进前的算法,改进后的Sage-Husa 自适应滤波算法在E 方向定位误差降低43.48%,N 方向定位误差降低31.33%,U 方向定位误差降低36.48%,且使误差波动更加平缓,增强自适应性的同时,提高了系统定位精度.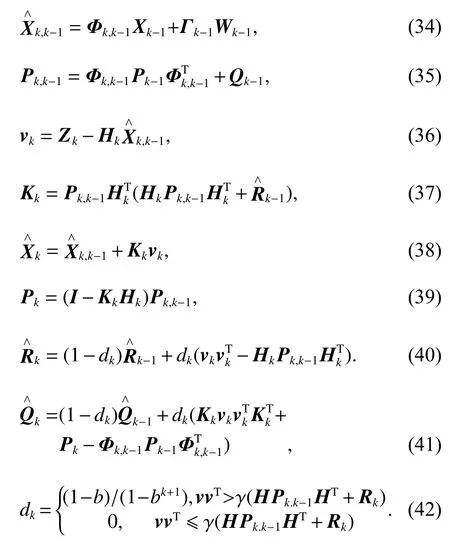
3 改进Sage-Husa 自适应滤波算法仿真与结果分析
3.1 仿真模块与仿真条件设置
3.2 仿真结果分析


4 结束语

