基于BP和RBF神经网络预测硬质阳极氧化膜的硬度

邢 翀，王坤昊

（1.长春金融高等专科学校信息技术学院，吉林长春130028；2.吉林师范大学计算机学院，吉林四平136000）

硬度是硬质阳极氧化膜的重要性能指标，与耐磨性能有着密切关系［1］。硬质阳极氧化过程中涉及的工艺参数较多，如电解液质量浓度、电解液温度、电流密度、氧化时间等。这些工艺参数及其交互作用对硬质阳极氧化膜的硬度有一定影响［2-4］，它们之前往往呈复杂非线性关系，采用常规数学建模方法很难准确表达。在此背景下，引入人工神经网络。研究表明，人工神经网络具有很强的适应性以及大规模并行处理和快速收敛的特性，解决复杂非线性问题具有优势［5-7］。

人工神经网络的种类较多，常用的是前馈神经网络、径向基函数神经网络、Kohonen自组织神经网络、递归神经网络、卷积神经网络和模块化神经网络。前馈神经网络中最具代表性的是BP神经网络，径向基函数神经网络中最具代表性的是RBF神经网络。目前，单独采用BP神经网络或RBF神经网络解决复杂非线性问题的报道较多［8-10］，但少有对这两种不同神经网络进行对比的报道。笔者创新性地将BP神经网络与通过两种不同方式构建的RBF神经网络进行对比研究，采用正交实验数据对不同神经网络进行训练，并通过对比相对误差，以期筛选出预测精度更高的神经网络。

1 研究思路

为了验证BP神经网络和RBF神经网络在氧化膜硬度预测方面的适用性，通过两种不同方式构建RBF神经网络。第一种方式是应用NEWRB函数构建RBF神经网络（以下简称NEWRB函数RBF神经网络），第二种方式是通过K-均值聚类法自行构建RBF神经网络（以下简称K-均值聚类RBF神经网络）。将不同神经网络进行对比，筛选出预测精度更高的神经网络。

具体研究思路如图1所示。第一步：通过正交实验获取原始数据。第二步：数据预处理，首先进行数据约简，提取影响氧化膜硬度的主要因素，降低维度数据，简化数据结构，然后对约简后的数据进行归一化处理，使各影响因素特征的分布基本一致，为后续构建神经网络创造条件。第三步：预处理后的数据应用于BP神经网络、NEWRB函数RBF神经网络、K-均值聚类RBF神经网络，在Matlab软件平台上进行仿真测试，通过对比相对误差筛选出预测精度更高的神经网络。

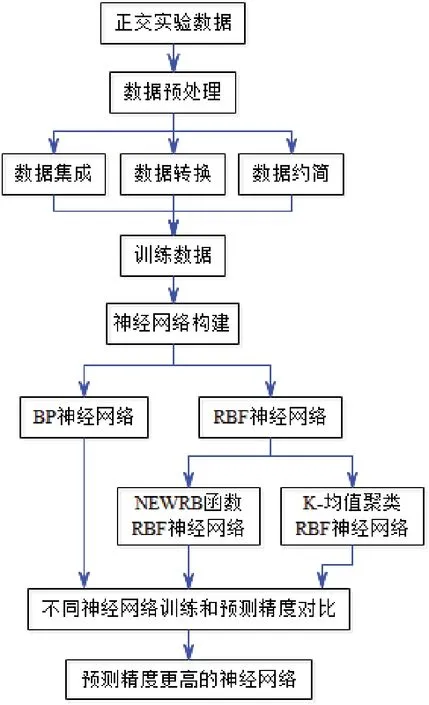
图1 研究思路Fig.1 Research approach

2 实验及数据预处理

2.1 基体材料

基材材料为2024铝合金，根据硬质阳极氧化实验要求，对2024铝合金进行预处理。首先用800#、1500#砂纸打磨，然后用碱液除油，接着用稀硫酸酸洗，最后用去离子水清洗，烘干后放在干燥箱中。

2.2 实验方法

采用硫酸与去离子水配成的电解液进行硬质阳极氧化实验，选用电流密度（F1）、氧化时间（F2）和硫酸质量浓度（F3）作为影响因素，氧化膜硬度（E）作为评价指标。为了减少实验次数并充分考察各个因素对氧化膜硬度的影响，采用正交实验设计法得到实验方案，如表1所示。

表1 实验方案Tab.1 Experimental scheme

2.3 实验结果

按照不同因素水平进行16组实验，采用MVTEST1000型全自动维氏硬度计检测不同氧化膜的硬度。加载为0.49 N，保持15 s后卸除。在每个试样表面选取3个点，检测结果取其平均值，如表2所示。

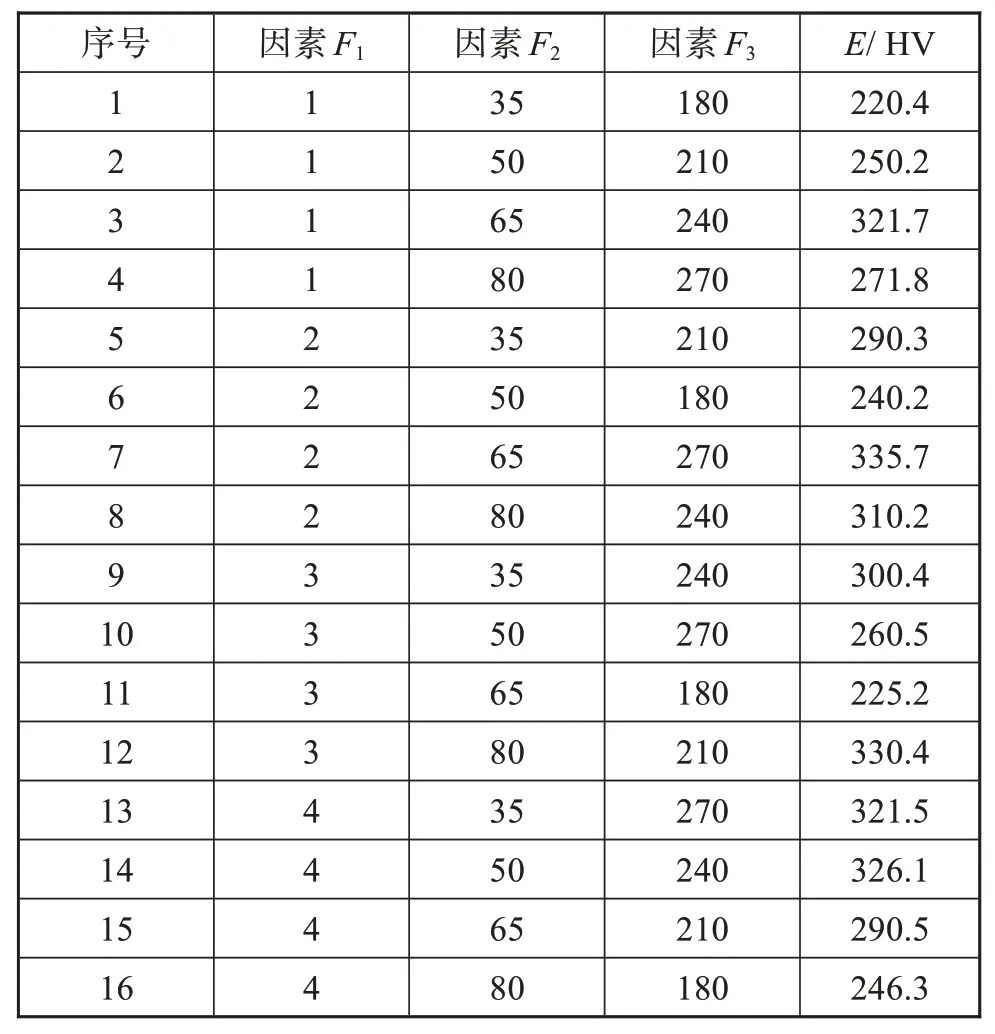
表2 实验结果Tab.2 Experimental results

2.4 实验数据归一化处理

为了消除数值问题满足求解需要，同时为了获得预期结果，需对实验数据进行归一化处理［11］，即将实验数据按照统一比例进行缩放，使其落入规定范围内。本文选择实验数据范围为［-1.1］，归一化处理采用如下公式：

3 BP神经网络构建与训练

本文构建的BP神经网络由输入层、隐含层和输出层构成，其结构如图2所示。输入层、隐含层和输出层的神经元数目分别为3、5、1，隐含层激励函数采用tansig函数，输出层采用Logsig函数，训练函数采用trainlm函数，调用Matlab软件工具箱内Newff（）函数建立神经网络。

将预处理后的数据输入神经网络进行训练，图3所示为BP神经网络训练过程。可见经过1274次训练后，均方误差达到期望值，说明训练完成。

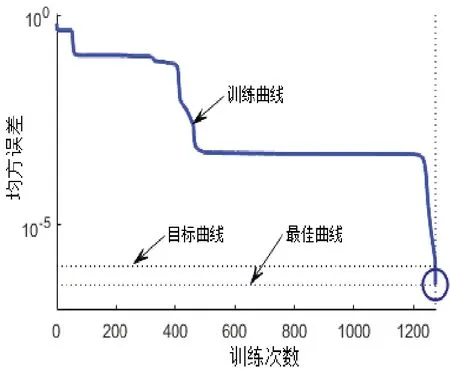
图3 BP神经网络训练过程Fig.3 Training process of BP neural network

4 RBP神经网络构建与训练

4.1 NEWRB函数RBF神经网络构建与训练

本文构建的NEWRB函数RBF神经网络也是由输入层、隐含层和输出层构成，如图4所示，其输入层神经元数目为3，输出层神经元数目为1，隐含层神经元数目由newrbe函数自动设置。为了更好的对比NEWRB函数RBF神经网络与BP神经网络的预测精度，将NEWRB函数RBF神经网络的目标函数设定与BP神经网络的目标函数一致。

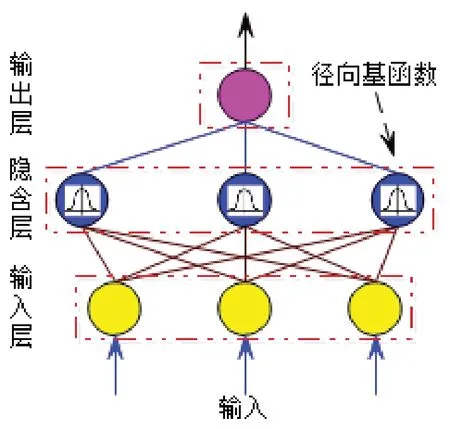
图4 RBF神经网络结构Fig.4 Structure of RBF neural network

调用Matlab软件工具箱内NEWRB函数建立神经网络，同样将预处理后的数据输入神经网络进行训练，图5所示为NEWRB函数RBF神经网络训练过程。可见经过865次训练后，均方误差达到期望值，说明训练完成。

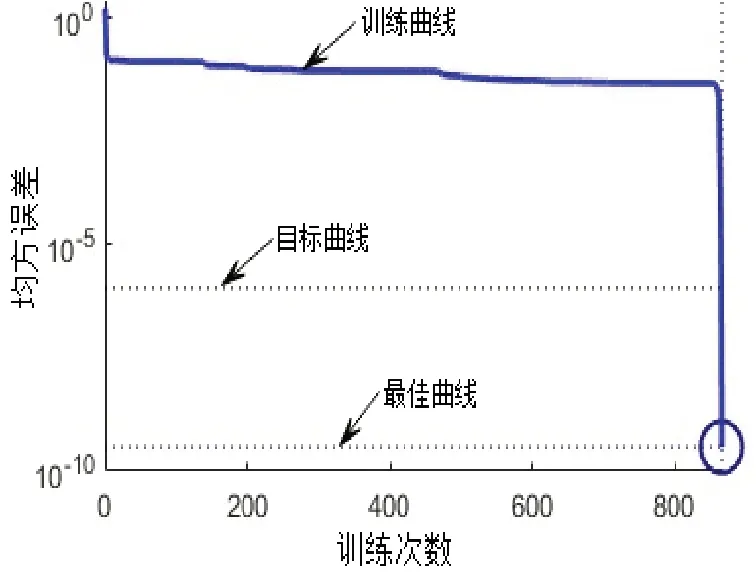
图5 NEWRB函数RBF神经网络训练过程Fig.5 Training process of NEWRB function RBF neural network

4.2 K-均值聚类RBF神经网络构建与训练

K-均值聚类RBF神经网络需使用K-均值聚类的方法确定径向基函数的中心［12］，首先采用dist指令计算输入各样本点与聚类中心点的欧式距离，然后根据中心聚类获取新的类内均值，并更新各类聚类中心，直至聚类中心不再变化后，再根据各中心之间的距离确定对径向基函数的扩展常数，采用最小二乘法计算RBF隐含层神经元输出的权值和阈值。

构建K-均值聚类RBF神经网络后，将预处理后的数据输入神经网络进行训练，图6所示为K-均值聚类RBF神经网络训练过程。可见经过975次训练后，均方误差达到期望值，说明训练完成。

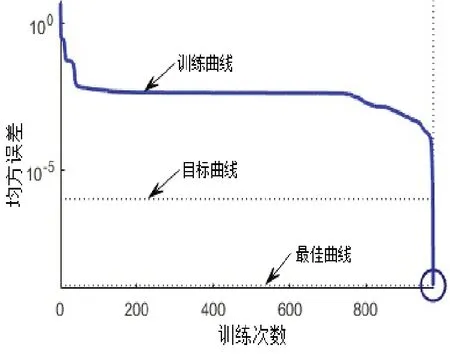
图6 K-均值聚类RBF神经网络训练过程Fig.6 K-mean clustering RBF neural network training process

5 预测结果及分析

采用构建的BP神经网络、NEWRB函数RBF神经网络和K-均值聚类RBF神经网络对氧化膜硬度进行预测，将16组实验数据输入不同神经网络中，得到预测结果，如图7所示。并将预测结果与实测值进行对比，得到相对误差，如表3所示。

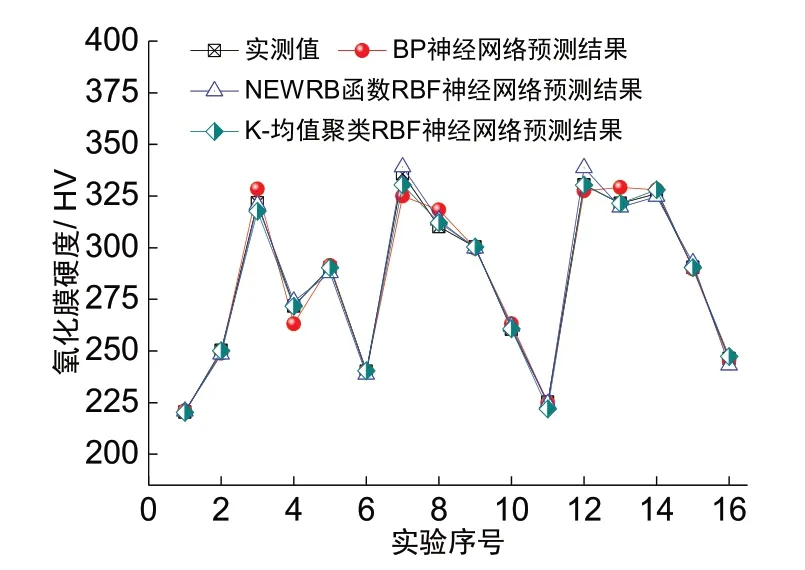
图7 不同神经网络的预测结果Fig.7 Prediction results of different neural network

由表3可知，BP神经网络、NEWRB函数RBF神经网络和K-均值聚类RBF神经网络的平均相对误差分别为1.13%、0.77%、0.40%，最大相对误差分别为-3.18%、2.48%、1.58%。与BP神经网络相比，NEWRB函数RBF神经网络和K-均值聚类RBF神经网络的平均相对误差和最大相对误差均较低，说明通过两种不同方式构建的RBF神经网络具有较高的预测精度，并且K-均值聚类RBF神经网络具有更高的预测精度。

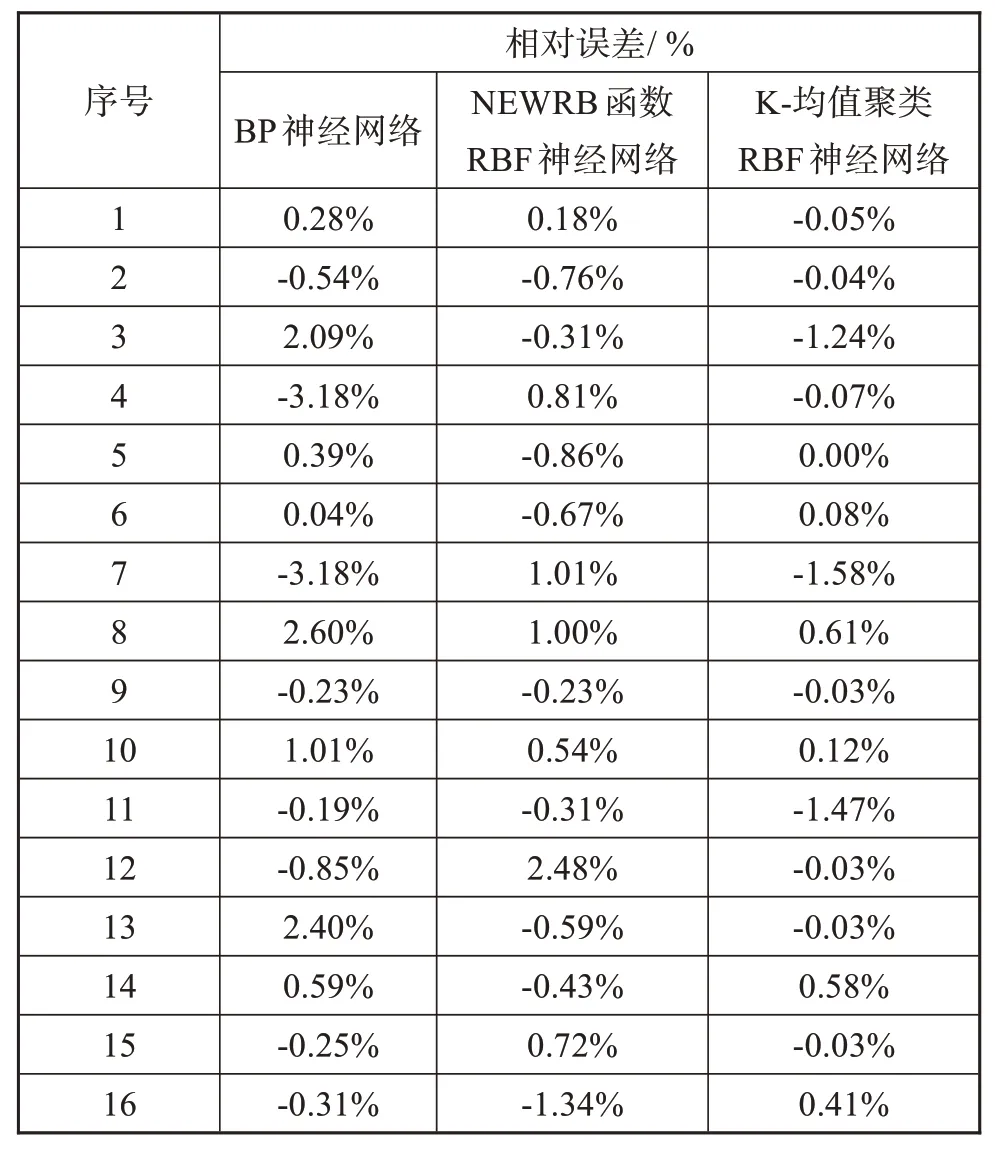
表3 不同神经网络的相对误差Tab.3 Relative errors of different neural network

6 结论

应用NEWRB函数和K-均值聚类法分别构建了NEWRB函数RBF神经网络、K-均值聚类RBF神经网络，采用正交实验数据训练完成后这两种不同神经网络的平均相对误差和最大相对误差均低于BP神经网络，都具有较高的预测精度。K-均值聚类RBF神经网络具有更高的预测精度，更适用于预测硬质阳极氧化膜的硬度。