地铁列车荷载作用下Duxseal-WIB隔振性能数值分析

李丹阳,高 盟,杨 帅,陈青生

(1.山东科技大学 山东省土木工程防灾减灾重点实验室,山东 青岛 266590; 2.山东科技大学 土木建筑学院,山东 青岛 266590;3.新加坡国立大学 土木与环境工程系,新加坡 119077)

0 引言

我国是全球地铁最发达的国家之一。地铁给人们出行带来便利的同时,也伴随着有关环境振动的困扰[1]。因此,如何评估地铁振动以及减小地铁振动带来的环境污染已成为国内外学者研究的热点。

列车运行引起的地基振动在计算理论方面已取得一定成果。如蔡袁强等[2]基于2.5维有限元法,分析了在列车移动常荷载作用下,轨道结构和周围饱和土体的动力响应特性。高广运等[3-4]提出2.5维有限元方程并建立轨道-地基模型,讨论了渗透系数、孔隙率等土体参数对地表位移振幅的影响规律。高盟等[5]对青岛地铁3号线和上海地铁10号线进行现场实测,对其进行动力响应分析并作对比,进而对地铁振动问题做出评价。张晓磊等[6]对京沪(北京至上海)高铁段开展大量的路基高架过渡段场地振动现场实测,分析了高铁振动在时域、频域的振动特性以及振幅的衰减规律。

而地铁隔振理论和方法主要有控制振源和在振动传播过程中采取隔振减振。如H.G.Wagner[7]研究了钢弹簧浮置板轨道在地面有轨电车隔振工程中的应用,发现其具有良好的隔振作用。吴天行[8]从振动源轨道结构出发,探索了不同轨道结构的隔振性能,并对比其隔振效果,得到轨道减振器-弹性支承块/浮置板轨道组合具有良好的隔振性能。孙晓静等[9]对列车-轨道结构耦合系统进行数值分析,得到了力传递率幅频和地基反力幅频特性曲线,并做出钢弹簧系数对乘车舒适度的评价。周凤玺[10]等对二维弹性地基波阻板隔振体系进行了理论解析分析,利用振幅衰减系数分析了波阻板参数及弹性波入射角度对隔振效果的影响。时刚等[11]针对被保护结构下埋置波阻板的远场被动隔振问题,采用频域弹性边界元法,推导得到了弹性地基中波阻板对入射Rayleigh 波散射的边界元方程,得出波阻板的弹性模量、埋置深度及厚度对隔振效果的影响。Jiang[12]讨论了在列车荷载作用下,隔振沟、板桩墙、阻波障等措施的隔振效果并分析隧道和地面的振动响应规律。邓亚虹等[13]基于动力学基本方程,对隔振沟进行弹塑性数值分析,发现改变其位置、埋置深度及宽度可改变隔振效果。高峰等[14]发现在隧道的减振层中采用注浆法可有效地提高隧道的隔振效果。黄胜[15]以嘎隆拉隧道为工程背景,采用数值模拟方法,讨论了橡胶和泡沫混凝土的隔振效果。但上述这些隔振理论和方法均有一定适用条件,如在施工、造价和隔振效率等方面都有一定的局限性。

Duxseal作为一种工业填料,不仅具有良好阻尼性能,吸收部分振动反射能,还具有高耐火性、耐腐蚀等优点,在减振的同时可提高使用场地的安全性与耐久性。Coe等[16]和Pak等[17]将Duxseal作为吸收振动反射能材料应用于动力离心模型箱内壁及大型土工离心机模型实验,发现Duxseal具有吸收振动能量的特性。高盟等[18-19]基于二维和三维半解析边界元法,计算空间均质弹性地基中Duxseal参数变化对地表位移振幅的影响,分析了Duxseal的隔振效果及性能,发现Duxseal与WIB的隔振规律具有互补性。

鉴于Duxseal材料具有优异的阻尼性能,本文提出蜂窝状波阻板(以下称HWIB)填充Duxseal的地铁隔振方法(DXWIB),并采用ABAQUS有限元计算程序,建立轨道-隧道-地基-DXWIB动力相互作用的三维有限元模型。分析WIB、HWIB和DXWIB的隔振性能并对比其隔振效果。此外,讨论DXWIB的埋置深度及厚度对隔振性能的影响,确定最佳隔振设计参数。

1 计算模型及参数

1.1 三维有限元模型的建立

基于ABAQUS数值计算软件,建立轨道-隧道-地层三维有限元模型,如图1所示。考虑到振动波在土体中的传播特性,模型沿线路纵向的长度为200 m,垂直轨道水平方向为100 m,高度为50 m。隧道为中等断面隧道,隧道外直径为6 m,内直径为6.65 m,隧道衬砌厚度为0.35 m,混凝土强度等级为C35。以青岛地铁为研究对象,土体共分为3层,自上而下分别为人工填土、黏土及粗砾砂、花岗岩,土层深度分别为4 m、10 m、36 m,以此近似模拟青岛地铁运行的地质条件。

图1 有限元模型Fig.1 Finite element computing model

隧道为单洞单线矿山法隧道,开挖深度25 m,一次初衬为0.20 m,二次初衬为0.15 m。钢轨采用60 kg·m-1标准钢轨,轨距为1.435 m;扣件一般按等间距布置,距离为650 mm;钢轨和扣件之间连接方式为弹簧阻尼器,扣件刚度的横向、垂向及纵向等效刚度分别为37.5、25、37.5 kN·m-1。WIB、HWIB和DXWIB的尺寸均为200 m(长)×4.2 m(宽)×0.50 m(高),其中后期模型计算中只改变埋深及高度参数。轨道板与基床表面、路基底面与土体之间采用“罚”接触,衬砌结构与土体之间通过Tie接触保持各接触面之间的变形协调。将地基土视为弹塑性材料,模型边界采用三维黏弹性人工边界条件[20]。

1.2 模型参数选取

在动力学计算中,关于土体的阻尼系数人们最常用的方法为瑞利阻尼法。本文中土体的阻尼系数参考文献[21]确定,各地层具体参数列于表1,模型其他计算参数列于表2。

表1 土层参数Table 1 Soil parameters

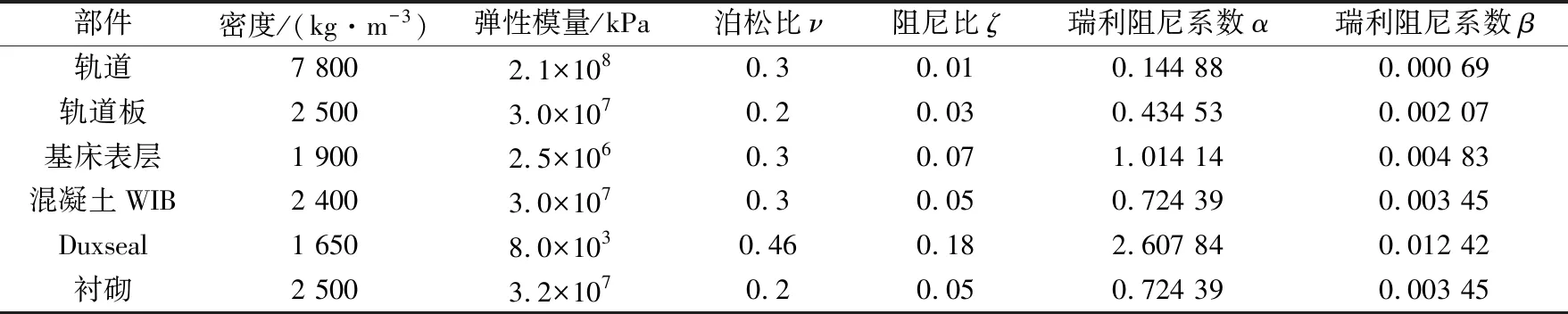
表2 模型其他参数Table 2 Other parameters of the model

1.3 模型监测点及计算参数的选取

为准确分析地铁振动对周围土体带来的动力响应规律,共选取11个监测点。通过编制DLOAD子程序实现地铁列车移动荷载的施加,车速为70 km/h。在隧道内基床表层选取5个监测点,以轨道中轴线为起点依次为:中心点、轨道正下方、1.5 m、2.0 m、3.0 m。地表选取6个监测点,以轨道中轴线为起点依次为:0 m、10 m、20 m、30 m、40 m、50 m。通过数值软件Abaqus分析各监测点的振动位移幅值、加速时程、频谱及Z振级曲线。在轨道正下方埋置一定深度及厚度的WIB[22],将HWIB替代WIB并分析各监测点的动力响应;然后将Duxseal材料填充于带孔波阻板,形成HWIB填充Duxseal(DXWIB)并改变其埋置深度(H)及厚度(B),分析其隔振效果。各隔振结构的埋深为距基床表层表面向下的垂直距离,埋置宽度大于轨道板的宽度即可,故本文选取4.2 m为固定宽度。各监测点及不同隔振结构埋置示意如图2所示。

图2 监测点及隔振结构埋置示意图Fig.2 Layout diagram of monitoring points and vibration isolation structure

为研究DXWIB的隔振性能,本文设计5组数值模拟试验,各组的计算参数详列于表3。

表3 数值模拟试验参数Table 3 Parameters for numerical simulation test

2 模型验证

为了验证本文模型建模方法的准确性,根据本文所述的三维有限元模型建立方法,选取文献[23]中实测地铁线路的土体力学参数和其他相关材料参数建立三维模型,并与文献中实测结果进行对比。分别提取浮置板和隧道壁的加速度时程曲线如图3、4所示。

从图3、4中可以看出,模型计算得到结果与文献中实测数据非常相似。模型计算得到的浮置板加速度值为18.08 m/s2,而文献中实测的加速度值为17.23 m/s2;模型计算得到的隧道壁加速度值为1.03 m/s2,文献中实测的加速度值为0.97 m/s2。实测和模型中的加速度曲线都出现了多处波峰,均在6～12 s时间段内出现,而在开始和结束的时间段内峰值趋于稳定。综合分析可知:模型的计算结果与文献实测结果吻合较好,可以验证本文中三维模型建模方法的合理性。

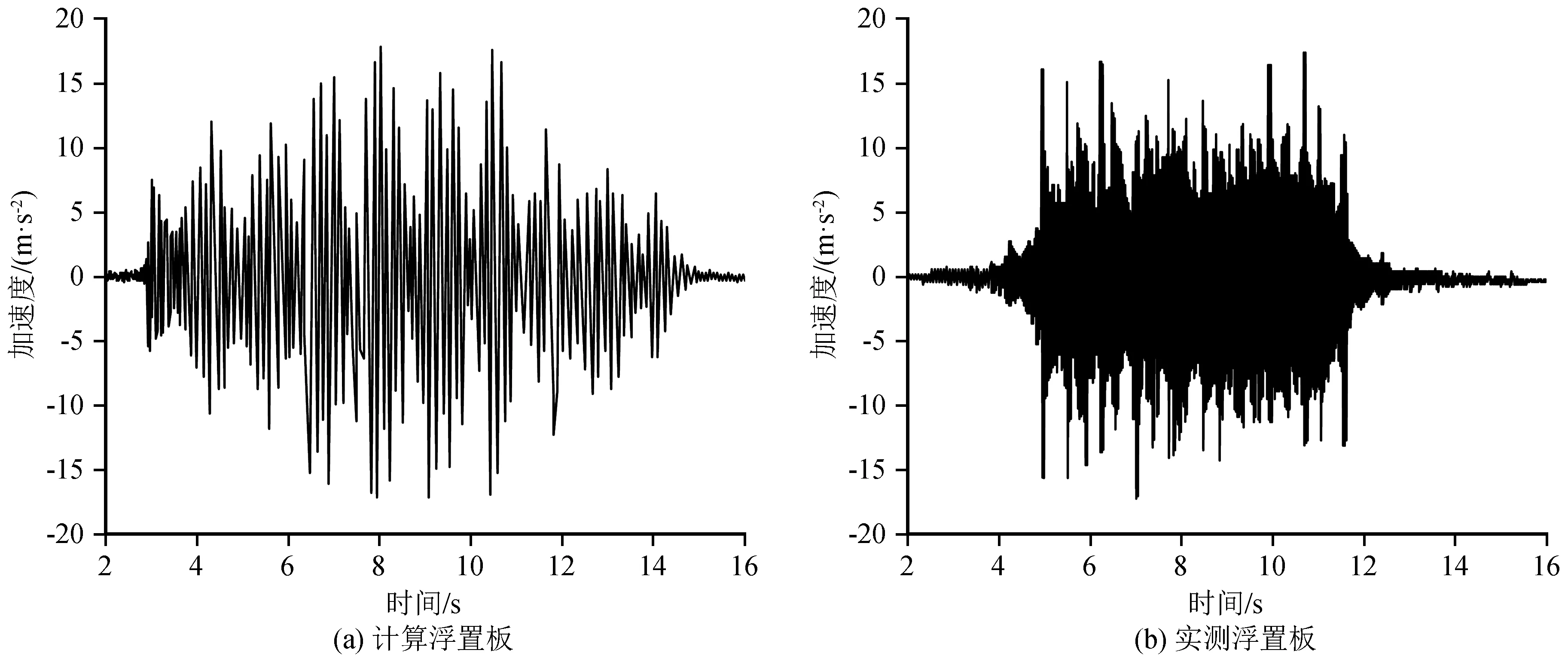
图3 浮置板加速度时程曲线对比Fig.3 Comparison of acceleration time history curves of floating plate

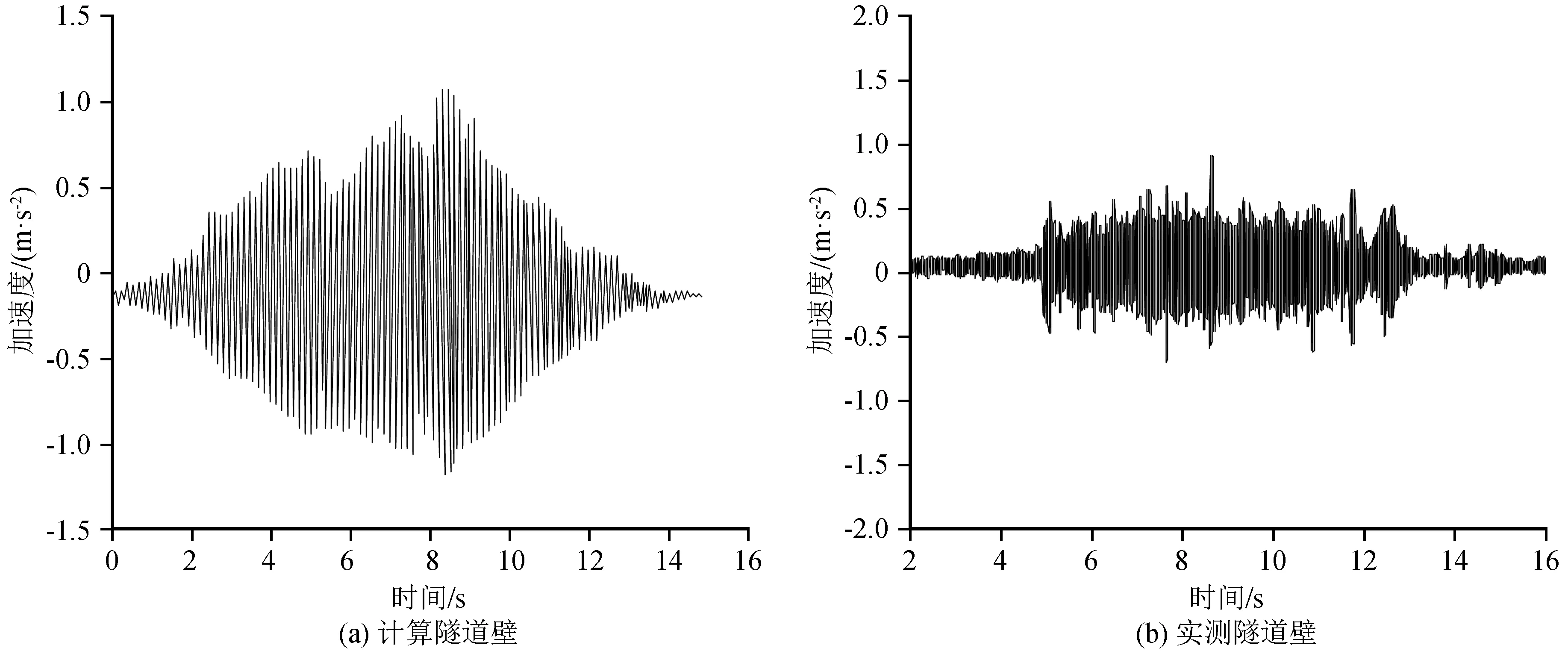
图4 隧道壁加速度时程曲线对比Fig.4 Comparison of acceleration time history curves of tunnel wall

3 环境振动响应分析

对于隔振效果的评价,Woods[24]提出用位移振幅衰减系数AR来衡量。AR定义为设置屏障后与未设置屏障时地表位移振幅之比,其表达式为:

其中,屏障为WIB、HWIB、DXWIB,无屏障则代表自由场。

AR=0,即设置屏障时位移振动幅值要远远小于未设置屏障时位移振动幅值,意味着隔振效果达到100%;若AR=1,即设置屏障时位移振动幅值与未设置屏障时位移振动幅值数值相等,有无屏障的隔振效果是一样的,即该屏障无隔振效果。

3.1 不同隔振结构效果对比

在模型中分别设置相同参数条件下的WIB、HWIB及DXWIB隔振结构,并与自由场对比分析各自的隔振效果。选取基床表层中的轨道正下方点为节点A,取距轨道中轴线40 m处为节点B。分别提取各节点的位移、加速度时程、频谱及Z振级曲线。

图5为各节点不同隔振结构振动位移幅值曲线。由图可知:对于节点A、B,DXWIB的振动位移幅值最小,自由场的振动位移幅值最大,WIB和HWIB的振动位移幅值很相近。其中节点A中的DXWIB振动位移幅值2.92 mm,相对于自由场振动位移幅值减小了24%;节点B中的DXWIB振动位移幅值0.62×10-2mm,相对于自由场振动位移幅值减小了29%。对于振动位移幅值而言,相同参数条件下DXWIB的隔振效果明显高于另外两种隔振结构,而WIB与HWIB的隔振效果非常相近。

图5 节点位移幅值曲线Fig.5 Displacement amplitude curve of each node

以上分析为一个监测点的位移变化曲线,可以看出所有隔振结构出现峰值位移时,计算时间不尽相同,在这里我们只关注位移最大幅值。以此类推,实际计算中基床表层和地表距轨道中轴线不同位置有相对应的监测点,由于篇幅有限,故不在文章中过多阐述。将所有监测点的最大位移幅值整合到一起,通过AR系数的表达式,即可计算出基床表层和大地地面的位移振幅衰减系数。

图6为基床表层及地表位移振幅衰减系数变化曲线。从图6可以看出,位移振幅衰减系数AR均小于1,这说明WIB、HWIB、DXWIB都具有一定的隔振效果。在基床表层中,位移振幅衰减系数随距离的增加趋于稳定状态。其中DXWIB的位移振幅衰减系数AR最小为0.31,即隔振效果为69%;同理可知WIB的隔振效果为45%,HWIB的隔振效果为47%。相反,地表位移振幅衰减系数的变化随距离的增加波动较大,出现多处波峰。DXWIB的位移振幅衰减系数AR最小为0.30,即隔振效果为70%;同理可知WIB的隔振效果为53%,HWIB的隔振效果为54%。综合分析可得,DXWIB相对于WIB、HWIB具有优异的隔振效果。

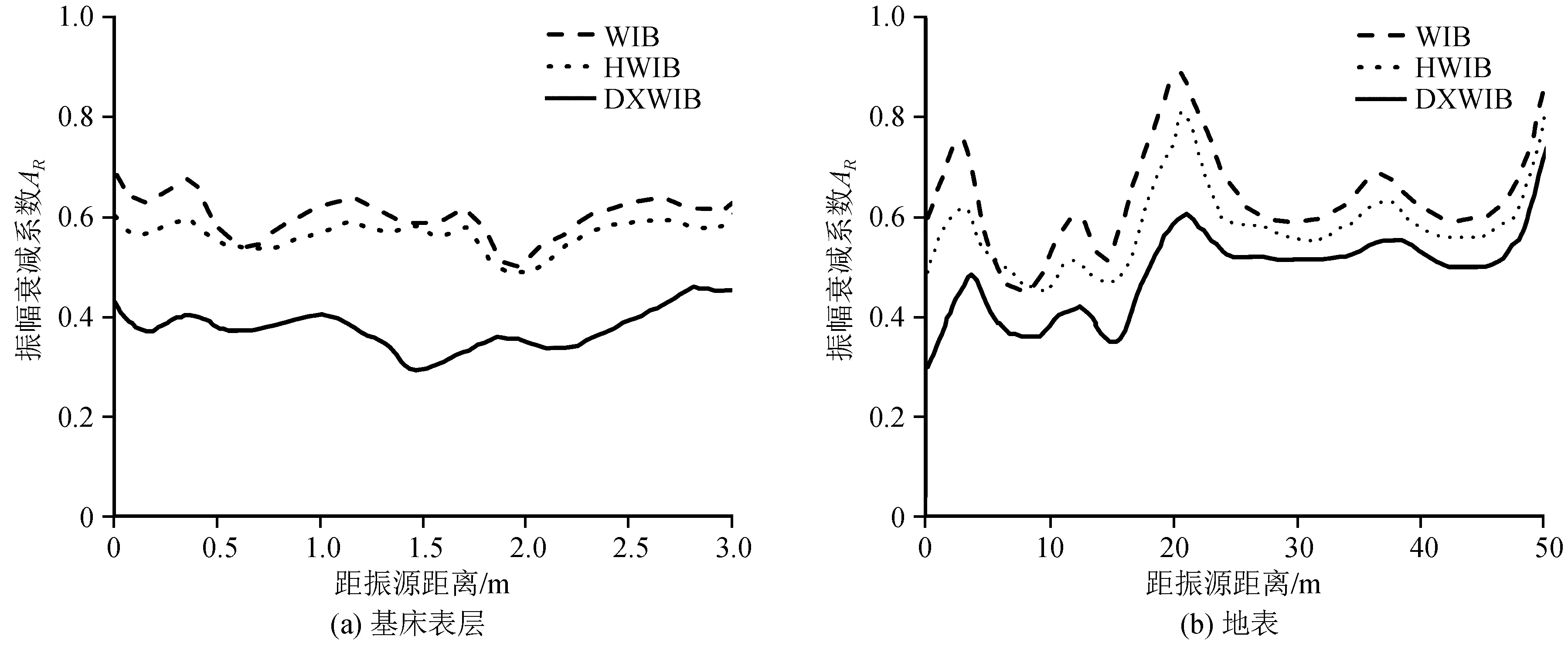
图6 位移衰减系数随距离变化曲线Fig.6 Curve of displacement attenuation coefficient with distance

由图7可知:对于WIB、HWIB、DXWIB三种不同隔振结构而言,节点A的加速度峰值分别为12.31 m/s2、11.87 m/s2、8.15 m/s2,DXWIB的加速度峰值相对于WIB、HWIB降低了32%左右;节点B的加速度峰值分别为10.32 mm/s2、9.59 mm/s2、6.12 mm/s2,加速度峰值降低了38%左右。峰值均在9～12 s时间段内,这说明列车此时恰好经过该监测点。综合以上分析可知Duxseal材料具有优异的隔振特性,而DXWIB具有更好的隔振性能。通过编写MATLAB程序,计算并绘制各节点的Z振级、频谱曲线。

图7 节点加速度时程曲线Fig.7 Acceleration time history curve of each node

图8为各节点Z振级曲线。从图中可以看出:三种隔振结构的Z振级变化曲线走势基本一致,WIB与HWIB的振级峰值比较接近,而DXWIB的振级峰值明显低于前二者,Z振级峰值所对应的振动频率为100～160 Hz。对于节点A,DXWIB的Z振级峰值最小,大小为106.1 dB,相对于WIB和HWIB分别减少约13 dB和12 dB,而节点B的Z振级峰值分别减少约6 dB和5 dB。

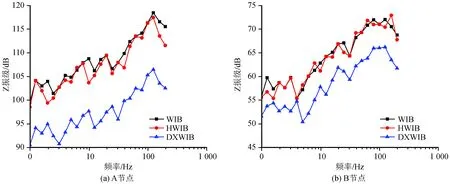
图8 不同节点处Z振级曲线Fig.8 Z vibration level curve at different nodes

节点A、B频谱曲线如图9所示。WIB、HWIB、DXWIB三种隔振结构加速度峰值所对应的主频率主要以中频为主,频率为100～150 Hz。由于各隔振结构的材料属性及参数设置不一样,所以该频率为不同隔振结构的特征频率。节点A在WIB、HWIB、DXWIB三种隔振结构下主导频率所对应的加速度分别为5.61 m/s2、4.89 m/s2、4.32 m/s2;B节点主导频率所对应的加速度分别为4.32 mm/s2、4.18 mm/s2、3.27 mm/s2。可以看出DXWIB隔振结构加速度峰值最小,说明了DXWIB具有一定隔振特性。

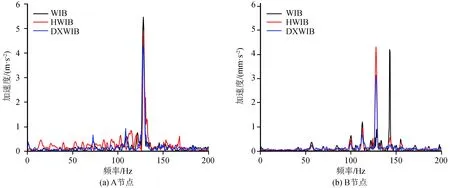
图9 不同节点处频谱曲线Fig.9 Spectrum curve at different nodes

3.2 不同试验参数下DXWIB的隔振效果对比

在模型中设置DXWIB,根据表3中的模拟试验参数,改变其埋置深度(H)及厚度(B)参数,分别获取并整理A、B节点的振动位移幅值、加速度时程、频谱及Z振级曲线,研究其隔振特性,确定最优隔振效果试验参数。

图10为各节点在不同试验参数下的振动位移幅值曲线。随着DXWIB埋深及厚度的增加,各节点的振动位移幅值整体呈先减小后增大的趋势。当DXWIB的埋深0.5 m、厚度0.8 m时A、B节点的振动位移幅值最小,分别为2.92 mm、0.62×10-2mm;埋深0.7 m、厚度1.2 m时的振动位移幅值最大,分别为3.43 mm、0.85×10-2mm。仅对振动位移幅值而言,DXWIB的最优试验参数为埋深0.5 m,厚度0.8 m。

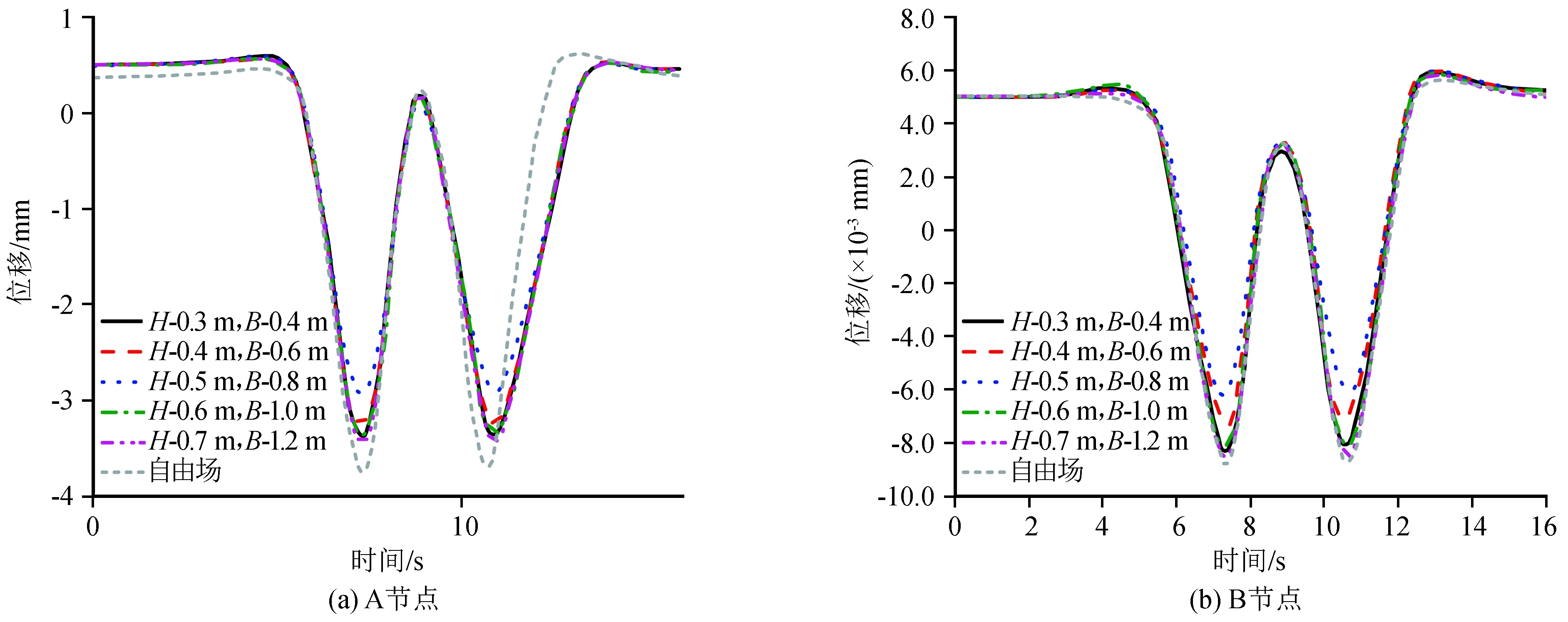
图10 不同试验参数振动位移幅值曲线Fig.10 Vibration displacement amplitude curves of each mode under different test parameters

图11为不同试验参数下基床表层和大地地表的位移振幅衰减系数变化曲线。由图可知:当埋深(H)0.5 m、厚度(B)0.8 m时,基床表层的振幅衰减系数AR最小为0.41,即隔振效果为59%;大地地表的振幅衰减系数AR最小为0.36,即隔振效果为64%。

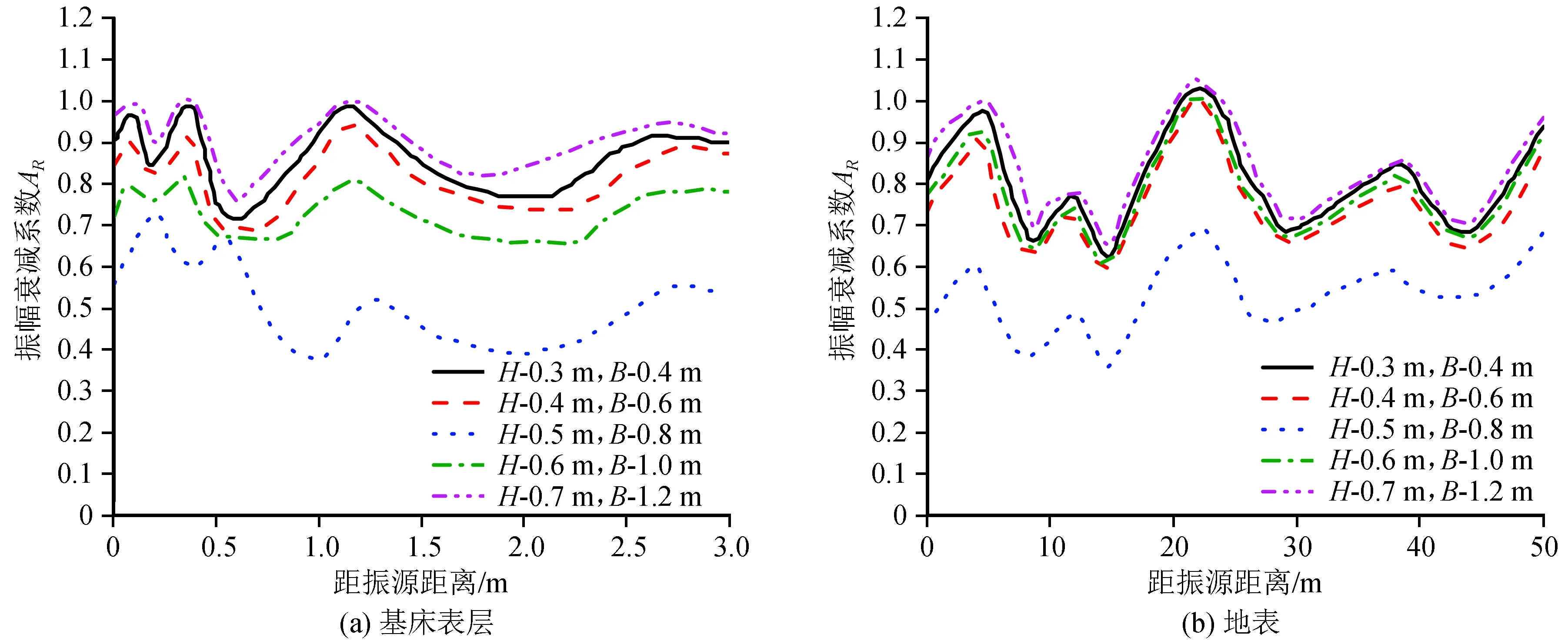
图11 不同试验参数的位移衰减系数随距离变化曲线Fig.11 Curve of displacement attenuation coefficient with distance for different test parameters

相对于其他试验参数,该试验参数的隔振效果明显提高。埋深(H)0.7 m、厚度(B)1.2 m时大地地表中出现了振幅衰减系数AR>1的情况,表明在该试验参数下,隔振效果与试验参数呈负相关,无隔振作用。因此,综合分析得到DXWIB的最优试验参数为埋深(H)0.5 m,厚度(B)0.8 m。

图12为各节点在不同试验参数下的频谱曲线,由图可知:A、B节点在各个试验参数下的频谱曲线变化趋势基本一致。当DXWIB的埋深0.3 m、厚度0.4 m时,A、B节点的主导频率分别为120 Hz、128 Hz,对应的加速度为3.37 m/s2、3.77 mm/s2;埋深0.4 m、厚度0.6 m时,A、B节点的主导频率分别为128 Hz、123 Hz,对应的加速度为2.66 m/s2、2.61 mm/s2;埋深0.5 m、厚度0.8 m时,A、B节点的主导频率分别为136 Hz、133 Hz,对应的加速度为2.68 m/s2、3.15 mm/s2;埋深0.6 m、厚度1.0 m时,A、B节点的主导频率分别为123 Hz、136 Hz,对应的加速度为2.32 m/s2、2.52 mm/s2;埋深0.7 m、厚度1.2 m时,A、B节点的主导频率分别为132 Hz、128 Hz,对应的加速度为2.11 m/s2、2.86 mm/s2。综合分析可知,对于基床表层和地表的加速度频谱而言,振动的主导频率也均在100～150 Hz。

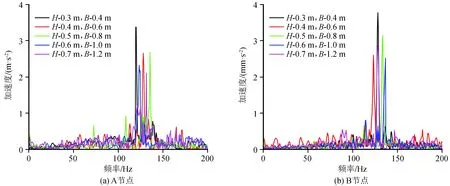
图12 不同试验参数频谱曲线Fig.12 Spectrum curves of each mode under different test parameters

图13为各节点在不同试验参数下的Z振级曲线。当DXWIB的埋深0.3 m、厚度0.4 m时,A、B节点的Z振级幅值分别为116.4 dB、70.2 dB;埋深0.4 m、厚度0.6 m时,Z振级幅值为109.7 dB、69.5 dB;埋深0.5 m、厚度0.8 m时,Z振级幅值为106.1 dB、66.8 dB;埋深0.6 m、厚度1.0 m时,Z振级幅值为112.3 dB、70.2 dB;埋深0.8 m、厚度1.2 m时,Z振级幅值为115.4 dB、71.6 dB。不难发现各工况条件下的Z振级幅值随着埋深及厚度的增加呈先衰减后增大的趋势。当埋深0.5 m、厚度0.8 m时,各节点的Z振级幅值最小,且均满足地铁噪声与振动控制规范要求。因此,当DXWIB的埋深为0.3 m、厚度为0.4 m时,隔振效果最好。

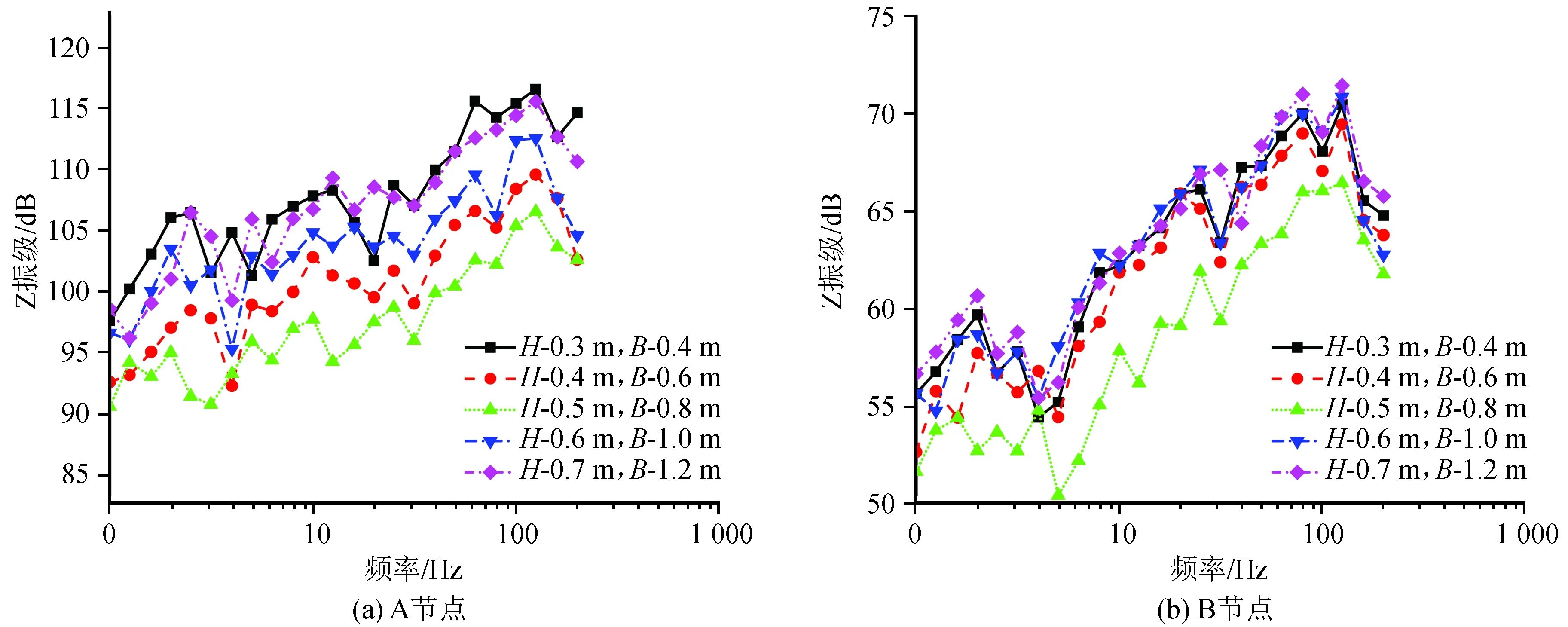
图13 不同试验参Z振级曲线Fig.13 Z vibration level curve of each mode under different test parameters

3.3 基床表层及大地地面振动响应规律

据调研,地铁列车时速一般为60～90 km/h。本文模拟的列车时速为70 km/h,这个数值是当下地铁运行的普遍时速,列车从刚进入模型隧道至完全驶出共历时16.49 s。为研究地铁列车移动荷载作用下周围环境的振动响应情况,选取垂直轨道方向的基床表层作为分析对象,以轨道中轴线为起点,一次选取中心点、轨道正下方、1.5 m、2.0 m、3.0 m为监测点,提取各点的振动位移幅值、加速度峰值及Z振级曲线。分析基床表层的振动响应规律,结果如图14所示。

图14 基床表层振动响应规律Fig.14 Vibration response law of surface layer of subgrade bed

图14(a)为加速度峰值变化曲线,各监测点的加速度峰值分别为10.91 m/s2、12.35 m/s2、8.52 m/s2、7.11 m/s2、5.97 m/s2。加速度振动规律表现为由振源向两侧横向传播中加速度峰值整体呈衰减趋势,且减小速率近似线性。说明列车振动荷载在基床表层中向远处传播时逐渐衰减。其中在轨道正下方处出现加速度最大值,主要原因为该点是主要轨道受力点。

图14(b)为各监测点的Z振级曲线,各监测点处振级峰值分别为110.2 dB、118.4 dB、110.1 dB、112.7 dB、111.6 dB,且满足地铁噪声与振动控制规范要求。Z振级主要振动频率为中频段,振级最大时振动频率约为125 Hz。

依次选取轨道正上方地表0 m、10 m、20 m、30 m、40 m、50 m位置处共6个监测点,分析地铁运行引起的大地地面的振动响应规律,如图15所示。

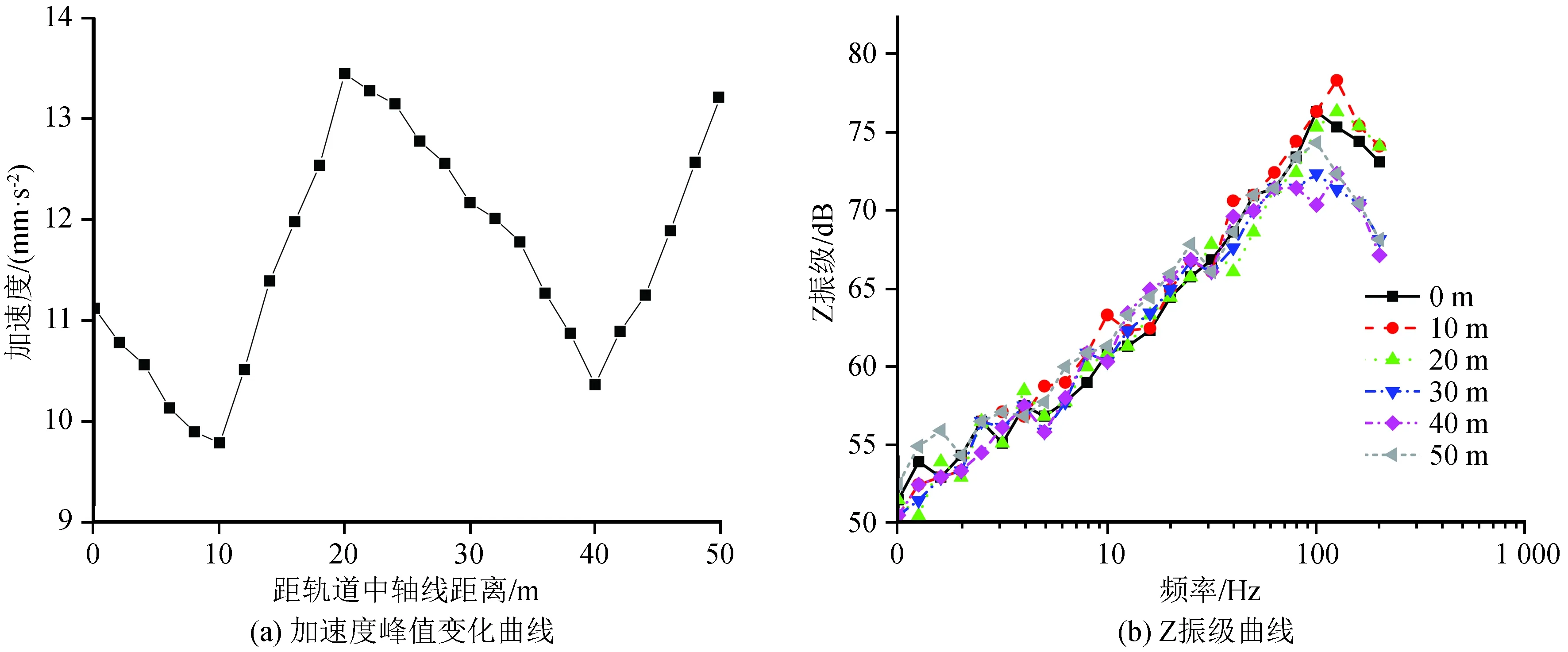
图15 地表振动响应规律Fig.15 Response law of earth surface vibration

轨道正上方地表各处监测点所对应的加速度峰值如图15(a)所示。加速度由振动源向两侧大地地面的传播过程中,加速度峰值呈先增大后减小再增大的趋势,在20 m和50 m处加速度峰值都存在放大现象。计算并绘制各监测点的Z振级曲线,如图15(b)所示,各监测点的Z振级峰值分别为76.7 dB、78.5 dB、76.5 dB、72.1 dB、72.3 dB、74.8 dB,其随传播距离的增加呈先增大后减小在增大的趋势。

对于振动放大现象出现的原因可能有以下两方面:一是土体特性对振动波传递的影响,不同土质条件下体波的传递特点也不一样;其次是受边界条件的影响,模型采用黏弹性边界条件,不能完全替代现实中的土体边界条件,对振动波有一定的反射作用。

4 结语

本文基于ABAQUS建立轨道-隧道-地层-DXWIB相互作用三维有限元模型,研究了HWIB填充Duxseal隔振系统(DXWIB)的隔振机理及其隔振性能,并对比分析DXWIB、WIB、HWIB的隔振效果。主要结论如下:

(1)相对于自由场,WIB和HWIB的隔振效果非常相近,而DXWIB的隔振效果明显提高。对于DXWIB基床表层的最大隔振效果达到69%,地表的隔振效果达到70%。证明DXWIB具有优异的隔振效果。

(2)当DXWIB的埋置深度为0.5 m、厚度为0.8 m时,位移振幅衰减系数AR最小,隔振效果最佳,基床表层和地表的隔振效果分别达到了59%、64%。

(3)基床表层的振动规律表现为由振源向两侧横向传播中,加速度峰值整体呈衰减趋势,轨道正下方加速度峰值及Z振级幅值最大,分别为12.35 m/s2和118.4 dB,主导频率约为125 Hz。

(4)振动源向两侧地表的传播过程中,加速度峰值呈先增大后减小再增大的趋势,在距轨道中轴线20 m和50 m处出现局部放大效应,应作为重点隔振区域。