往复荷载作用下锈蚀钢筋混凝土柱黏结滑移模型及数值模拟研究

王 斌,吕 斌,丁一爽,孙勇峰,王家滨

(1.西安工业大学建筑工程学院,陕西 西安 710021;2.西安建筑科技大学 西部绿色建筑国家重点实验室,陕西 西安 710055)

0 引言

钢筋混凝土(reinforced concrete,RC)框架柱作为框架结构主要的承重及抗侧力构件,其钢筋与混凝土间良好的黏结性能是确保结构安全的基础[1-2]。在复杂环境下(如:近海大气环境),由于RC构件长期遭受氯离子侵蚀导致内部钢筋发生锈蚀并逐步引发混凝土保护层开裂,从而降低了钢筋与混凝土之间的黏结性能,削弱了二者之间的协同工作能力,最终导致RC结构整体服役寿命缩减。

目前,国内外就往复荷载作用下锈蚀RC框架柱的黏结性能、承载力及耗能等抗震性能开展了大量试验研究[3-5],但由于试验方法和RC结构锈蚀环境的不同,导致最终试验结果存在一定的差异。此外,由于试验研究所能提供的数据有限,借助数值模拟分析作为试验研究的有效补充方法受到了广大科研工作者的青睐。而往复荷载作用下的锈蚀钢筋与混凝土之间的黏结滑移(τ-s)本构模型是确保地震作用下锈蚀RC结构滞回性能数值模拟准确性的关键因素之一。现有研究结果中对于锈蚀钢筋与混凝土之间τ-s本构模型的建立大多基于单调荷载作用[6-8],而对于往复荷载作用下锈蚀钢筋与混凝土之间的τ-s本构模型研究较少,且已有文献研究结果表明[9-10]:拉-压往复循环荷载作用下锈蚀钢筋混凝土构件的黏结滑移外包络线退化规律与单调荷载作用下未锈蚀构件τ-s曲线外包络线退化规律相似。文献[11]基于单调荷载下梁式拔出试验及已有的往复荷载作用下未锈蚀RC构件τ-s外包络曲线,同时引入钢筋锈胀压应力对模型中参数进行修正,建立了往复荷载作用下锈蚀钢筋混凝土τ-s本构模型。但上述τ-s本构模型的建立或基于特定梁式试验,或模型计算中的部分参数难以通过现有试验进行准确定义;另外,目前针对往复荷载作用下锈蚀钢筋混凝土框架柱的黏结滑移本构模型研究较少。因此,采用现有研究成果不能较好的反映锈蚀RC柱在往复荷载下的滞回特性。

鉴于此,本文基于人工模拟气候环境下锈蚀RC框架柱低周往复加载试验结果,建立往复荷载作用下锈蚀钢筋混凝土τ-s本构模型,利用ABAQUS有限元分析软件建立试件的数值分析模型,对所建立的τ-s本构模型的可靠性进行验证,通过计算结果与试验结果进行对比分析,进一步对所建立模型中的黏结退化参数进行修正,最终建立适用于往复荷载作用下锈蚀RC框架柱的τ-s本构模型。研究结果可为地震作用下锈蚀钢筋混凝土结构的数值分析计算提供理论参考。

1 τ-s本构模型的建立

已有研究发现[9-10]:当控制滑移量和加载循环次数较小时,单调荷载作用下锈蚀RC试件τ-s本构曲线与往复循环荷载作用下锈蚀RC试件τ-s外包络曲线趋势相吻合且退化规律相似。因此,本文假设往复循环荷载作用下锈蚀钢筋混凝土τ-s外包络线可以采用单调荷载作用下锈蚀钢筋混凝土τ-s曲线进行替代,且锈蚀钢筋τ-s曲线退化规律与未锈蚀钢筋相同,从而建立往复荷载作用下锈蚀钢筋混凝土框架柱τ-s本构模型。

1.1 单调荷载作用下锈蚀RC框架柱本构模型

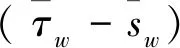
(1)

(2)

1.2 往复荷载作用下未锈蚀RC框架柱本构模型

往复循环荷载作用下未锈蚀钢筋混凝土τ-s本构关系曲线模型如图1所示[13]。该模型假设所有的正负向循环加载黏结滑移曲线均关于原点对称,式(3)即为图1中三段式包络线OAUR表达式:

(3)

式中:τu为极限黏结应力;su为极限黏结应力对应的滑移量;K3为下降段UR的刚度;τr为残余黏结应力;sr为达到残余黏结应力时的滑移量,对应于图中R点滑移量。

根据图1往复循环加载黏结滑移曲线,包络线OABCA′B′C′代表第一次循环至预定滑移量sA和s′A时的黏结滑移曲线。B点和B′点所对应的黏结应力τB、τB′和滑移量sB、sB′可通过式(4)～式(7)进行计算:

图1 往复循环加载黏结滑移曲线Fig.1 Bond-slip curve under cyclic loading

τB=-αfτA

(4)

sB=sA-(τA-τB)/K4

(5)

τB′=-αfτA′

(6)

sB′=sA′-(τA′-τB′)/K4

(7)

式中:τA和τA′分别为A点和A′点的黏结应力,可通过预定滑移量sA代入公式(3)进行计算;αf为摩擦黏结应力衰减系数,取αf=0.12;K4为卸载刚度,本文中K4=295 N/mm3。该模型假设所有的正负向循环加载黏结滑移曲线均关于原点对称,因此有τA=-τA′,τB=-τB′。

第二次加载循环C′DEFD′E′F′及后续的加载循环中特征点处对应的黏结应力和滑移量可按式(8)和式(9)进行计算。

τD=-αdτA

(8)

sD=sA-(τA-τD)/K4

(9)

(10)

式中:τD和sD分别为D点的黏结应力和相对滑移量。同理,D′点的黏结应力和相对滑移量亦可按上式(8)和式(9)进行计算;αd为与循环加载次数N相关的黏结退化系数。

1.3 往复荷载作用下的锈蚀RC框架柱τ-s模型

将图1中的黏结滑移外包络线OAUR采用单调荷载作用下锈胀开裂钢筋混凝土黏结滑移本构关系[式(1)]进行替代,得到往复荷载作用下锈胀开裂钢筋混凝土黏结滑移包络曲线计算式,具体表达式如式(11):

(11)

式中:τw,sw分别为锈胀裂缝宽为w时的黏结应力和相对滑移量;τcr,w为残余黏结应力;scr,w、su,w、sr,w分别为出现滑移时、达到极限荷载时及出现水平段时的相对滑移量;k1～k7为试验常数,具体定义为:

(12)

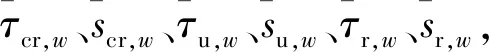
2 模型的有效性分析

基于课题组前期进行的锈蚀RC柱往复加载试验[14],采用ABAQUS有限元分析软件建立锈胀开裂RC柱有限元模型,将数值计算所得滞回曲线与试验滞回曲线进行对比,以验证上述建立的锈蚀钢筋与混凝土间τ-s本构模型的适用性。

2.1 试验概况

课题组前期试验试件以RC框架结构底层柱为设计原型,共设计6榀剪跨比为5的RC框架柱试件,试件制作养护完成后采用人工模拟气候环境对其进行加速锈蚀(见图2),以轴压比n和试件混凝土表面纵向锈胀裂缝宽度w为变化参数。待试件达到预期锈蚀程度后,采用荷载-位移混合加载制度对锈蚀RC框架柱施加水平往复循环荷载。试件具体尺寸及配筋形式如图3所示。钢筋和混凝土的材料力学性能分别见表1和表2所列。具体试验过程及相关参数详见文献[14]。

图2 试件加速腐蚀现场Fig.2 Accelerated corrosion test of specimens

图3 试件尺寸及截面(单位：mm)Fig.3 Dimensions and cross-section of specimens (Unit:mm)

表1 混凝土材料力学性能Table 1 Mechanical properties of concrete

表2 钢筋材料力学性能Table 2 Mechanical properties of reinforcement

2.2 数值模型的建立

2.2.1 材料本构模型

(1)受锈蚀箍筋约束混凝土本构模型

混凝土材料属性复杂,准确输入其本构模型,对有限元分析结果有重大影响,本文采用课题组前期氯离子侵蚀下RC棱柱体抗压试验得到的约束混凝土应力-应变全曲线[15],具体表达式如下:

(13)

A=Ehε′0/σ′0

(14)

(15)

式中:σ为混凝土压应力;ε为混凝土的压应变;A为应力-应变曲线上升段参数;σ′0为受箍筋约束混凝土的峰值应力;ε′0为峰值应力σ′0所对应的应变;α为应力-应变曲线下降段参数;Eh为混凝土初始弹性模量;ε′0.5为受锈蚀箍筋约束混凝土曲线下降段最大应力下降50%时的极限应变。

(2)锈蚀钢筋本构模型

锈蚀钢筋采用考虑钢筋锈蚀率的两折线σ-ε曲线,具体表达式如下:

(16)

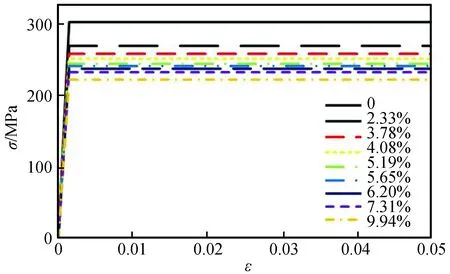
图4 锈蚀钢筋σ-ε曲线Fig.4 σ-ε curve of corroded rebar

(3)锈胀开裂钢筋混凝土黏结滑移本构模型

往复循环加载下锈蚀钢筋与混凝土之间的黏结滑移本构关系采用式(11)作为外包络线,第一次和第N次加载循环中特征点处对应的黏结应力和滑移量按式(4)～式(10)进行计算。

此外,结合本次锈蚀RC柱拟静力往复加载试验,可知:纵向钢筋锚固总长度la=1 000 mm,但由于各试件最终均在柱脚部塑性铰区域(距柱脚部约300 mm)发生破坏,因此纵向钢筋锚固位置取

l=300 mm,代入式(2)可求得黏结锚固位置函数ψw(l)的值,如式(17)。

(17)

2.2.2 锈蚀RC柱数值模型

通过ABAQUS有限元软件对试验试件进行数值模拟分析,本次数值模拟计算共选取4榀试验试件,分别对应的试件编号:C-1(n=0.2,w=1.0)、C-2(n=0.4,w=1.0)、C-3(n=0.6,w=1.0)、C-5(n=0.4,w=0.5)。根据所选取试件的特点,为节省数值计算成本提高建模精度,本文选取如表3所示的材料单元类型,并通过ABAQUS用户子单元程序的程序接口将上述本构模型添加进对应单元的材料特性里。

表3 材料的单元类型Table 3 Unit type of material

模型的建立以锈蚀RC框架柱试件实际尺寸、钢筋布置形式,采用分离式建模方法建立分析模型,网格划分尺寸0.05 m,如图5。试验加载中应确保框架柱底端固定,因此数值模拟边界条件采用对称柱底嵌固。在加载求解过程中经过反复调试,荷载子步数设置为400～600,收敛容差5%。

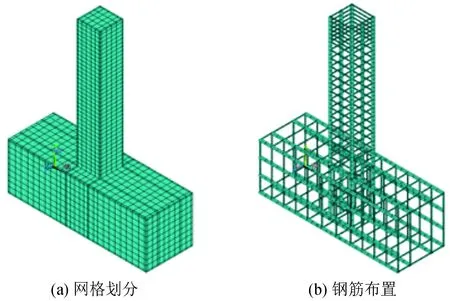
图5 钢筋混凝土数值模型Fig.5 Numerical model of RC columns

2.3 模型的有效性分析

为确保数值计算结果的准确性,在建模分析过程中严格按照试验设计参数进行定义。图6为4组试件数值计算结果与试验滞回曲线对比结果。

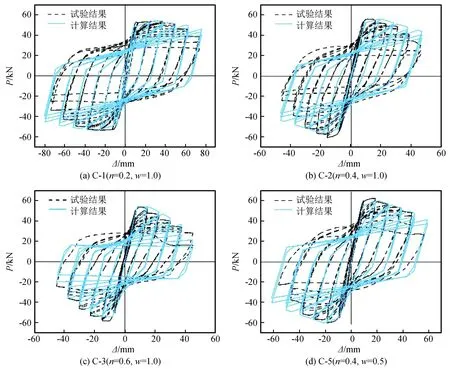
图6 数值模拟结果与试验滞回曲线对比Fig.6 Comparison of numerical simulation results and test hysteresis curves

可以看出,数值计算所得滞回曲线与试验滞回曲线存在较为明显的差异:与试验滞回曲线相比,数值计算所得滞回曲线正负向加载呈对称分布,而实际加载过程中由于试件存在残余变形导致滞回曲线不对称;往复循环加载初期,数值计算滞回曲线和试验滞回曲线吻合度较高,当加载循环次数N>15时,在相同的位移幅值下,计算所得滞回曲线的水平荷载明显高于试验值,说明此阶段锈蚀钢筋与混凝土黏结强度无明显退化,此现象与实际试验结果不相符;达到峰值荷载后,试验滞回曲线强度和刚度退化较数值模拟曲线更为显著;当轴压比n=0.6、锈胀裂缝宽度w=1.0时,试验滞回曲线与数值计算滞回曲线吻合度相对较高,这是由于在较大的竖向荷载作用下,试件整体刚度有所提升,在一定程度上抑制了锈蚀钢筋与混凝土之间的黏结强度劣化。

综上所述,基于现有的单调荷载作用下锈胀开裂钢筋混凝土τ-s本构和往复荷载作用下未锈蚀τ-s本构外包络曲线所建立的往复荷载作用下锈胀开裂钢筋混凝土τ-s本构模型[式(11)]并不能完全有效的反映往复循环荷载作用下锈蚀钢筋混凝土柱的滞回特性。同时,结合上述对比结果进一步分析发现,当加载循环次数和水平位移幅值较大时,所建立黏结滑移本构模型中的黏结强度退化速率相比于实际情况较慢,而模型中能够体现加载循环次数和不同位移幅值对黏结强度退化速率影响的主要是摩擦黏结应力衰减系数αf和黏结退化系数αd,因此,本文接下来的内容将对αf和αd做进一步修正,以建立更为合理的往复荷载作用下的锈胀开裂钢筋混凝土τ-s本构模型。

3 参数修正及有效性验证

3.1 摩擦黏结应力衰减系数αf的修正

已有研究表明[11-12],对于不同锈蚀程度的钢筋而言,锈蚀钢筋与混凝土接触界面的变化及混凝土对锈蚀钢筋握裹力变化均会对摩擦黏结应力衰减系数产生较大影响。对于锈蚀程度较小的试件,锈蚀产物使钢筋与混凝土的接触面变得更为密实,会使摩擦黏结应力衰减系数的值增大;对于钢筋锈蚀程度较大,进而造成混凝土保护层锈胀开裂的试件,对应混凝土对钢筋的握裹力降低,导致摩擦黏结应力衰减系数随之减小。研究指出[17-18],当钢筋锈蚀后,混凝土对锈蚀钢筋的握裹力又可采用锈蚀产物对混凝土保护层的锈胀压应力来表示,则摩擦黏结应力衰减系数又可表示为下式:

(18)

式中:p(x)和p(0)分别为锈蚀深度为x和0时所对应的锈胀压应力。对于受箍筋约束的锈胀开裂钢筋混凝土试件,当锈蚀深度为x时的锈胀压应力p(x)可按下式进行计算。

p(x)·R0=H+Fstx

(19)

(20)

(21)

(22)

式中:R0为未锈蚀钢筋半径;H为与锈蚀深度x有关的函数;fct为混凝土劈裂抗拉强度;εct为混凝土锈胀开裂时的拉应变;Rc为纵向钢筋轴心到混凝土保护层表面的距离,Rc=R0+c;εθc为锈蚀深度为x时混凝土保护层开裂的环向应变;n为锈蚀钢筋体积膨胀率,通常n=2～4;Fstx为锈蚀箍筋对混凝土的约束力,nst为锚固区箍筋的数量;dst为未锈蚀箍筋的直径;nd为纵向钢筋的数量;Sst为箍筋之间的间距;Ast为未锈蚀箍筋截面面积;fstx和Estx分别为箍筋锈蚀后的屈服强度和弹性模量。

而对于公式(21)中锈蚀深度x值的确定,若采用直接测量的方法,则难度较大,已有研究表明,可通过混凝土表面锈胀裂缝宽度w和钢筋截面面积损失量ΔAs间接地计算锈蚀深度x值。法国学者Vidal基于经受氯盐喷雾干湿交替侵蚀长达12年之久的锈胀开裂RC梁试件试验数据,并结合已有的理论计算模型,提出了一种基于混凝土锈胀裂缝宽度来计算锈蚀钢筋截面损失量的新模型[16],具体表达式如下:

w=K(ΔAs-ΔAs0)

(23)

(24)

(25)

式中:ΔAs为锈蚀钢筋平均截面面积损失量;ΔAs0为引发混凝土保护层锈胀开裂所对应的锈蚀钢筋截面面积损失量;拟合系数K=0.057 5;α为坑蚀集中系数,对于均匀锈蚀钢筋,α=2,对于氯离子侵蚀环境下的非均匀锈蚀钢筋,α=8;x为锈蚀钢筋坑蚀深度;As为未锈蚀钢筋截面面积;c为混凝土保护层厚度;d为钢筋初始直径。

根据本次试验实测的钢筋直径d、混凝土保护层厚度c以及未锈蚀钢筋截面面积As,采用公式(24)计算得到引发混凝土保护层锈胀开裂所对应的锈蚀钢筋截面面积损失量ΔAs0=3.373 6 mm2为固定值,将实测锈胀裂缝宽度w和ΔAs0代入式(23)计算出锈蚀钢筋截面面积损失量ΔAs,如下表4所列。从表中可以看出按Vidal模型计算的锈蚀钢筋截面面积损失量与试验值相差较大,所以该式不适用于锈胀开裂RC柱锈蚀钢筋截面损失量的计算。

此外,通过分析课题组前期试验中实测锈胀裂缝宽度w和锈蚀钢筋截面损失量(ΔAs-ΔAs0)的分布发现,两者呈线性关系,如图7所示。因此本文进一步对w和(ΔAs-ΔAs0)的关系进行线性拟合,得到锈胀裂缝宽度和钢筋截面损失量之间的关系式(26),拟合优度系数R2=0.952 57,其具体表达式如下:

图7 试件裂缝宽度与钢筋截面损失量拟合关系Fig.7 Fitting relationship between crack width and loss of reinforcement section

w=0.119 43(ΔAs-ΔAs0)+0.403 66

(26)

式中:锈胀裂缝宽度w根据实际测量得到,则公式(26)可再次表达为关于锈蚀钢筋平均截面面积损失量ΔAs:

(27)

按式(27)计算得到的不同锈胀裂缝宽度下的锈蚀钢筋截面面积损失量ΔAs计算值如表4所列。可以看出,相较于Vidal模型来说,本文所建立的计算式(27)更适用于锈胀开裂RC柱钢筋截面损失量的计算,且根据式(27)和式(25)可进一步计算得到钢筋锈蚀深度x的值。

表4 钢筋截面损失量计算值与试验值对比Table 4 Comparison between the calculated and tested values of the loss of reinforcement section

3.2 黏结退化系数的修正

由于本次锈胀开裂RC柱拟静力往复加载试验采用荷载-位移混合加载制度,在荷载控制阶段,每级荷载作用下加载循环一次;柱脚部纵筋屈服后换为以位移控制加载,每级位移幅值下循环加载三次。所以,对黏结退化系数的修正除考虑每级荷载或位移幅值下加载循环次数的影响外,还应综合考虑加载时控制位移幅值的影响。因此综合考虑加载控制位移幅值和加载循环次数双因素的黏结退化系数如式(28)所示[19]:

(28)

式中:SA为加载控制位移幅值;N为每级荷载或位移幅值下的加载循环次数。

3.3 修正后模型验证

采用上述修正后的摩擦黏结应力衰减系数和黏结退化系数替换原模型中的αf[式(4)和式(6)]和αd[式(8)],再次以试件C-1、试件C-2、试件C-3、试件C-5为原型建立锈胀开裂RC柱有限元分析模型,通过修正前后计算结果与试验结果的对比分析以验证修正后模型的有效性,数值计算结果和试验结果对比如图8所示。

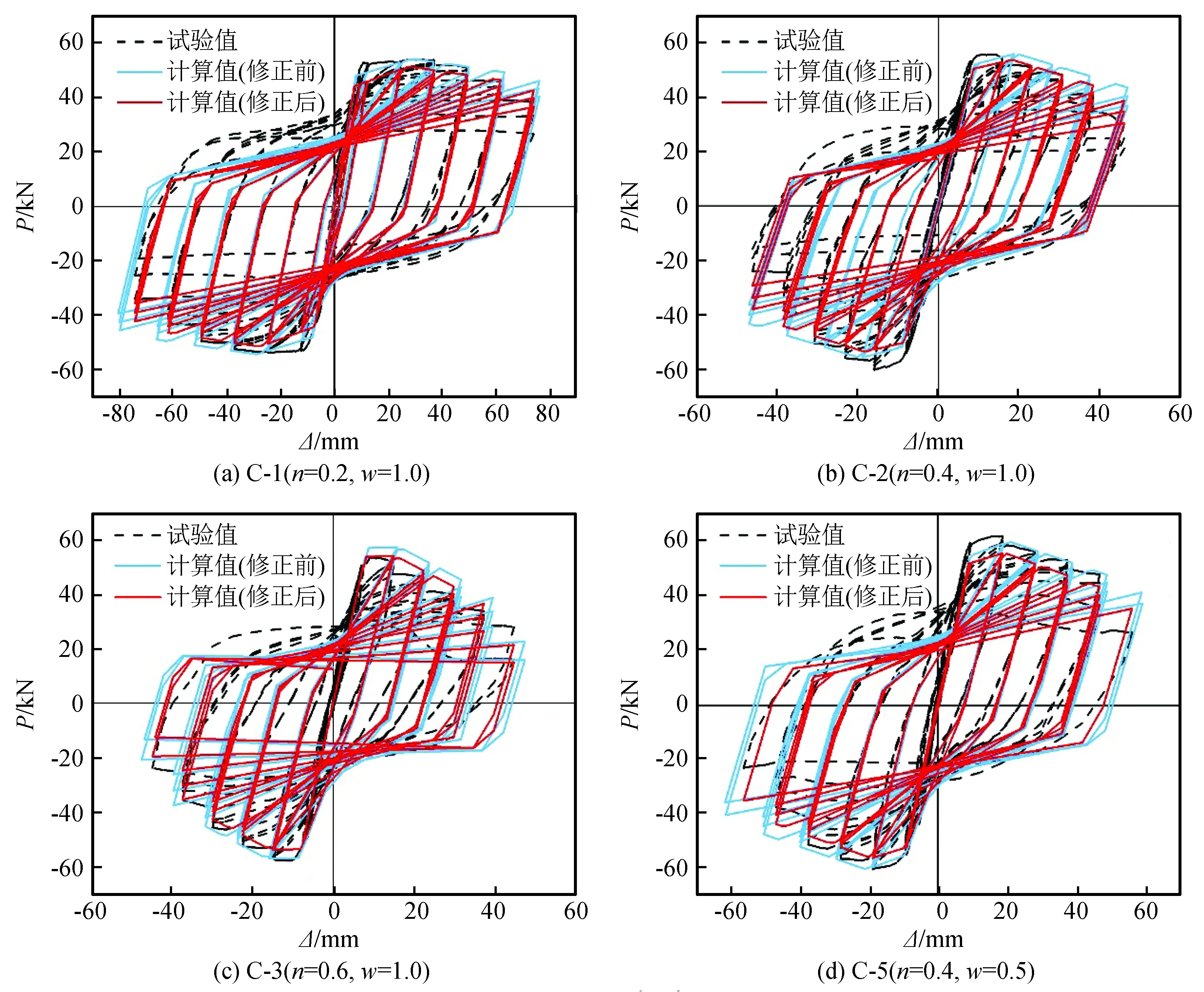
图8 修正前后计算结果与试验滞回曲线对比图Fig.8 Comparison of the calculated results and the experimental hysteresis curves before and after correction

可以看出:修正后的模型计算滞回曲线与试验滞回曲线吻合度相较图6在非对称性和黏结强度退化等方面有了较为显著的改善,数值模拟结果更加可靠和有效;与试验滞回曲线相比,修正后的模型滞回曲线峰值荷载略低于试验值,这是由于修正后的黏结退化系数在原模型的基础上还综合考虑了加载控制位移幅值对黏结退化系数的影响,当加载制度改为位移控制时,每级循环下黏结强度下降较大,导致峰值荷载降低;当加载循环次数N>22时,试验滞回曲线较模拟计算的滞回曲线下降更快,这是由于在试件在加载过程中出现较大的残余变形,导致强度下降速率加快。总的来说,与未修正的往复荷载作用下锈胀开裂钢筋混凝土τ-s本构模型相比,修正后的τ-s本构模型考虑的影响因素更为全面,能够更为有效地反映锈胀开裂RC柱在往复荷载作用下的滞回性能。

4 结论

本文基于课题组前期试验研究结果和已有研究成果,采用数值模拟分析方法,对锈蚀钢筋混凝土框架柱的黏结滑移本构模型进行系统的研究,得到以下结论:

(1)采用已有的单调荷载作用下的锈蚀钢筋混凝土τ-s曲线代替往复荷载作用下的未锈蚀钢筋混凝土τ-s外包络线作为往复荷载作用下的锈蚀RC试件τ-s本构模型,与试验滞回曲线相比存在较为明显的误差。

(2)通过引入锈胀压应力和加载位移控制幅值分别对摩擦黏结应力衰减系数和黏结退化系数进行修正,并且对于锈胀压应力在计算时所需要的钢筋锈蚀深度x可根据混凝土锈胀裂缝宽度和锈蚀钢筋截面面积损失量的关系计算,该计算方法中的各参数意义明确、计算形式简洁,且修正后摩擦黏结应力衰减系数和黏结退化系数所考虑的影响因素更全面,能够更为有效的反应锈胀开裂RC柱在往复荷载作用下的黏结性能变化。

(3)由于修正后的摩擦黏结应力衰减系数和黏结退化系数考虑了锈胀裂缝宽度和钢筋截面损失量之间的关系以及加载控制位移幅值和加载循环次数的影响。因此,数值计算滞回曲线与试验曲线吻合度更高,说明本文所建立的锈蚀钢筋混凝土柱黏结滑移本构模型能够有效地反映锈胀开裂RC柱在往复荷载作用下的锈蚀和钢筋之间的黏结性能变化,可为往复荷载作用下锈蚀RC结构精确化数值建模分析提供理论参考。