基于时间点过程的时间序列预测模型
郭全盛,李 栋,张 蕾,魏楚元
(北京建筑大学电气与信息工程学院,北京 100044)
1 引言
近年来,随着城市不断扩张,诸如环境污染、疾病爆发、交通事故和能源消耗、社会暴力和种族矛盾等问题日益加剧,给城市精细化管理带来许多负面影响。城市发展具有复杂性、阶段性、区域性、相对性等特点,涉及经济、社会、环境、文化和空间等诸多方面的问题,是国家“十四五”规划中城镇化可持续发展、空间优化与提升、创新社会治理能力等战略需求的重点与难点。基于城市计算的数据挖掘算法研究,是解决具有时间属性、动态发展的城市问题的有效方法,精准预测城市时序事件未来发生的概率、时间和地点等,对于政府避免、控制或减轻相关的社会风险是有益的。
城市中发生的异步时序事件以某种方式彼此关联,可以从历史事件的时间数据中挖掘出用于预测事件未来发展趋势的信息,为有关部门提供合理的决策支撑,进行有针对性的资源调配、规划布局等,以提高生产效率和经济效益。因此,研究城市中事件的依赖关系和预测问题具有重要的科学意义和应用价值。
时间点过程TPP(Temporal Point Process)是对连续时间域上异步离散事件序列建模分析的最有用的数学工具,通过其条件强度函数(即危险函数)来表征历史事件对未来的影响。最常见的时间点过程模型中,假设条件强度函数具有特定的参数形式(例如泊松过程[1]、霍克斯过程[2 - 4]等指数形式),等价于假设事件间隔服从指数分布,忽略了对历史数据的普遍依赖性,限制了条件强度函数表达式的灵活性。部分学者提出基于深度学习算法中的递归神经网络RNN(Recurrent Neural Network)的时间点过程模型[4,5],通过RNN来获得对历史事件的特征表示,将条件强度函数建模为RNN中隐藏状态的函数。基于RNN的模型在预测性能上优于参数形式的模型,然而此类模型的表达能力受限于对条件强度函数的假设,且错误的假设会降低预测精度。
为了解决上述问题,本文提出基于递归神经网络和累积危险函数的时间点过程模型RC-TPP(RNN-Cumulative hazard function TPP),该模型将条件强度函数表示成一种通用形式。首先利用前馈神经网络对条件强度函数的积分(即累积危险函数)进行建模,能够有效避免对条件强度函数的特定假设;然后求导获得条件强度函数。这种方法既能得到关于条件强度函数的灵活模型,又能精确地计算包含条件强度函数积分的对数似然函数,不需要进行数值逼近,减少了计算成本,提高了预测精度。本文的主要贡献包括以下方面:
(1)提出了基于积分求导法的条件强度函数式,提高了序列预测精度。
(2)构建了基于递归神经网络和累积危险函数的时间点过程模型。通过RNN捕获历史事件的非线性依赖关系,利用全连接网络FCN(Full Connected Network)获得累积危险函数。
(3)选择具有代表性的合成数据集和真实数据集对所提出的模型进行性能分析。实验结果表明,本文提出的模型可以更好地进行时间序列预测,效果优于其它模型。
2 相关工作
许多社会活动可被描述为连续时间域上的异步离散事件序列,如交通事故、金融交易和暴力犯罪等,如何预测此类事件发生的概率、时间和地点,是一个具有挑战性的重要问题,在城市管理、交通优化等领域有着广泛的应用前景。时间点过程正是预测异步离散事件序列最有效的数学工具,已成为国内外学术研究和产业应用的热点。下面对相关研究工作进行概述。
时间点过程是由一系列代表事件发生时刻的点组成的序列,传统方法是假设其中的条件强度函数具有特定的参数形式。霍克斯过程是一种可以捕捉突发现象的时间点过程模型[2],该模型指出,未来事件发生的概率受历史事件的影响,且随时间呈指数衰减;目前,霍克斯过程已被广泛用于时间序列的预测研究。Bacry等人[4]将霍克斯过程用于金融领域,估计交易过程的数据级波动,在预测金融风险、稳定市场方面具有良好的效果。文献[5]针对高频金融数据,建立了背景率随时间变化的霍克斯过程,背景参数由贝叶斯方法来估计,该模型可以捕捉宏观经济消息发布后的快速时变。上述研究均假设事件会依照某种规律发生,即将时间点过程模型设定为具有某种固定的发展趋势,限制了模型的表达能力;然而,一旦假设错误,势必降低预测精度。
近年来,越来越多的研究者将神经网络用于时间点过程的研究中,提出了大量基于神经网络的时间点过程模型。Du等人[6]提出递归标记时间点过程预测模型,核心思想是将时间点过程的条件强度函数视为历史事件的非线性函数,采用递归神经网络自学习历史事件的影响。文献[7]提出的条件强度函数包括背景函数和历史函数2部分,分别由2个递归神经网络对事件背景和历史效果进行建模,以捕捉长期时间动态关系。Mei等人[8]对连续时间上的离散事件进行建模,构造了神经自调节的多变量点过程模型,可以预测何时会发生哪种类型的事件。Jing等人[9]提出基于长短期记忆网络的时间点过程模型,用于预测人们的活动轨迹,该模型采用分段常数函数作为条件强度函数。文献[10]采用蒙特·卡罗法逼近积分,运用强化学习算法推导出基于策略梯度的时间点过程模型,在时间序列预测方面的表现与文献[7]中的模型效果相当。文献[11]提出了一种灵活的策略梯度算法,将异步随机离散事件的行为和反馈嵌入到深度递归神经网络的实值向量中。Huang等人[12]基于递归神经网络和隐马尔可夫模型RNN-HMM(Recurrent Neural Network-Hidden Markov Model),设计了递归泊松过程,将时间点过程看作一系列时间间隔内泊松过程的集合,其条件强度函数根据历史编码声音信号的隐藏状态而变化。Li等人[13]基于卷积神经网络和自注意力机制,设计了新的时间序列预测模型,提高了强长期依赖性的时间序列预测精度。Rangapuram等人[14]设计了基于时间序列预测的深度状态空间模型,将状态空间模型和深度学习相结合,通过采用联合学习的递归神经网络对每个时间序列的线性状态空间模型进行参数化。由上述研究可知,基于神经网络的时间点过程模型在预测性能方面优于特定参数形式的模型。
众所周知,时间点过程的激励制度是计算对数似然函数,包含对条件强度函数的积分,因此难以获得精确的估计。为了克服这一局限性,本文首先利用前馈神经网络对条件强度函数的积分进行建模,而不是对函数本身进行建模;然后再对累积危险函数求导,还原条件强度函数;最后,通过对合成数据和真实数据的分析,表明了模型的有效性。本文构建的时间序列预测模型,在无需数值逼近运算的情况下,可以精确计算对数似然函数,实现对事件的精准预测。
3 时间点过程
3.1 传统的时间点过程
时间点过程是由一系列事件发生时刻的点组成的序列,是时间数据的一种序列表达形式,此过程由条件强度函数λ表示。在时间点过程中,事件在时刻t发生的概率是历史事件Ht的条件强度函数值,如式(1)所示:
(1)
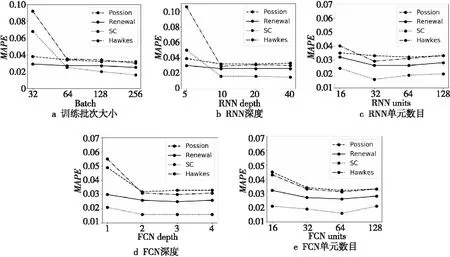
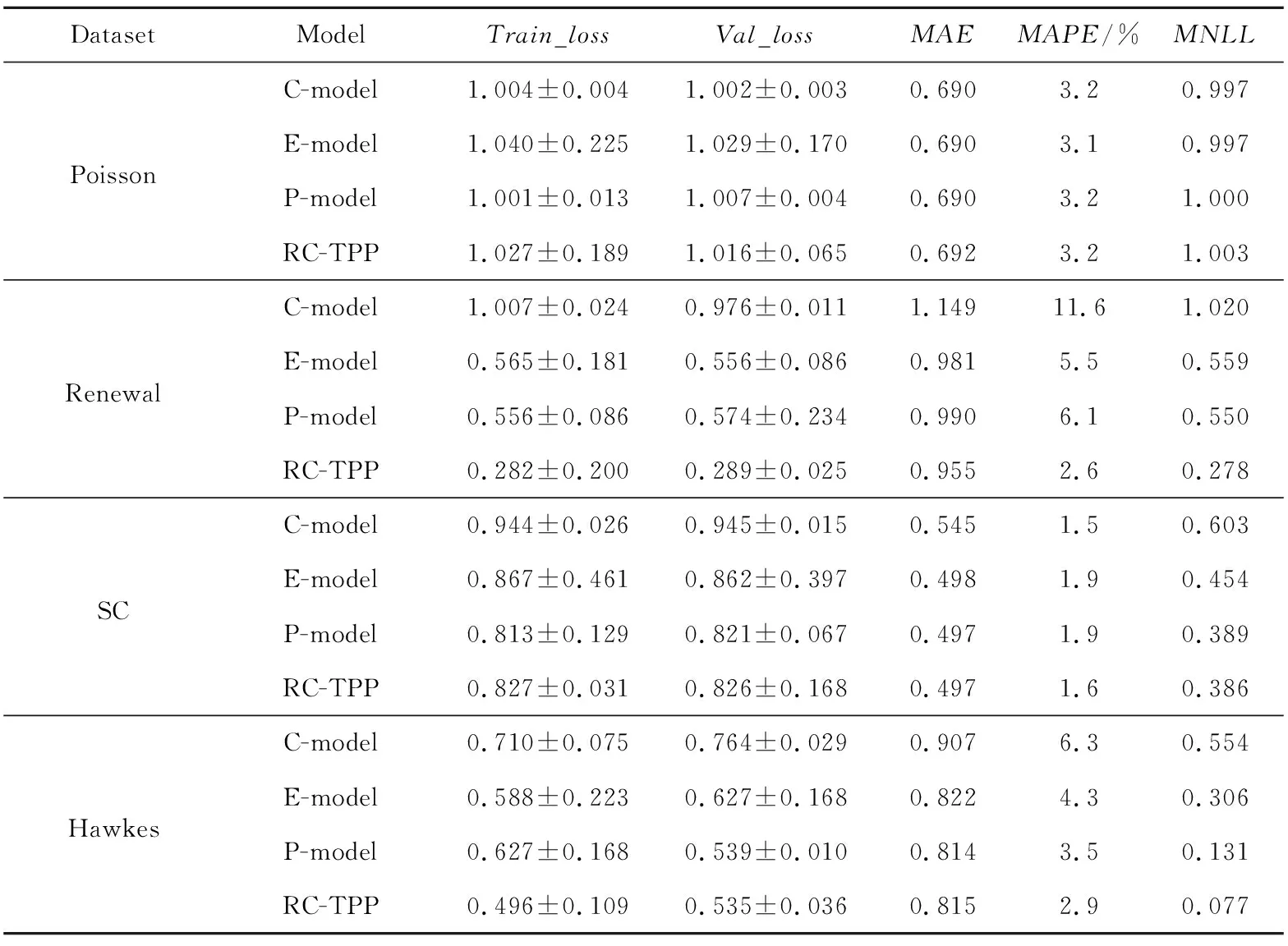
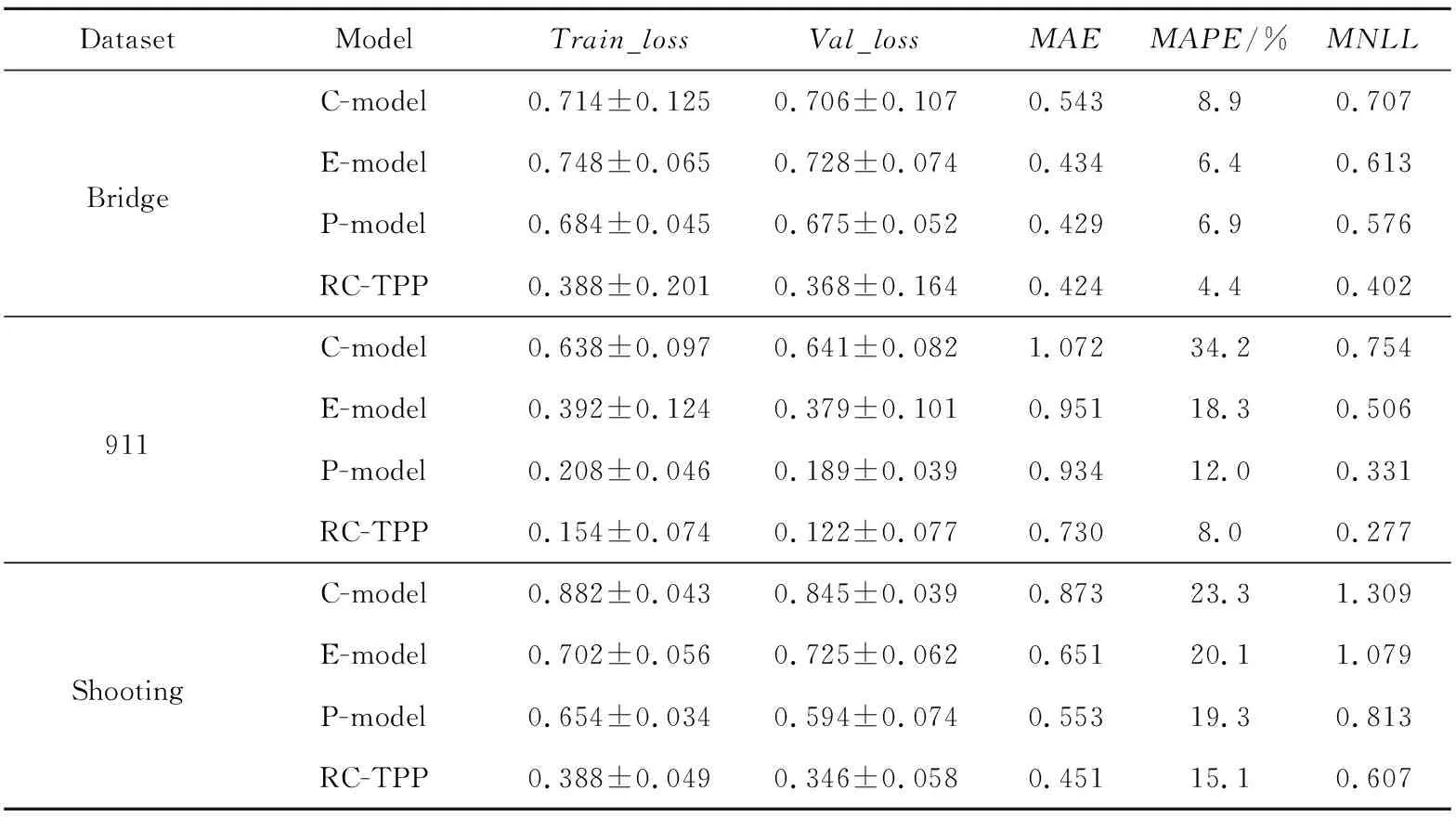
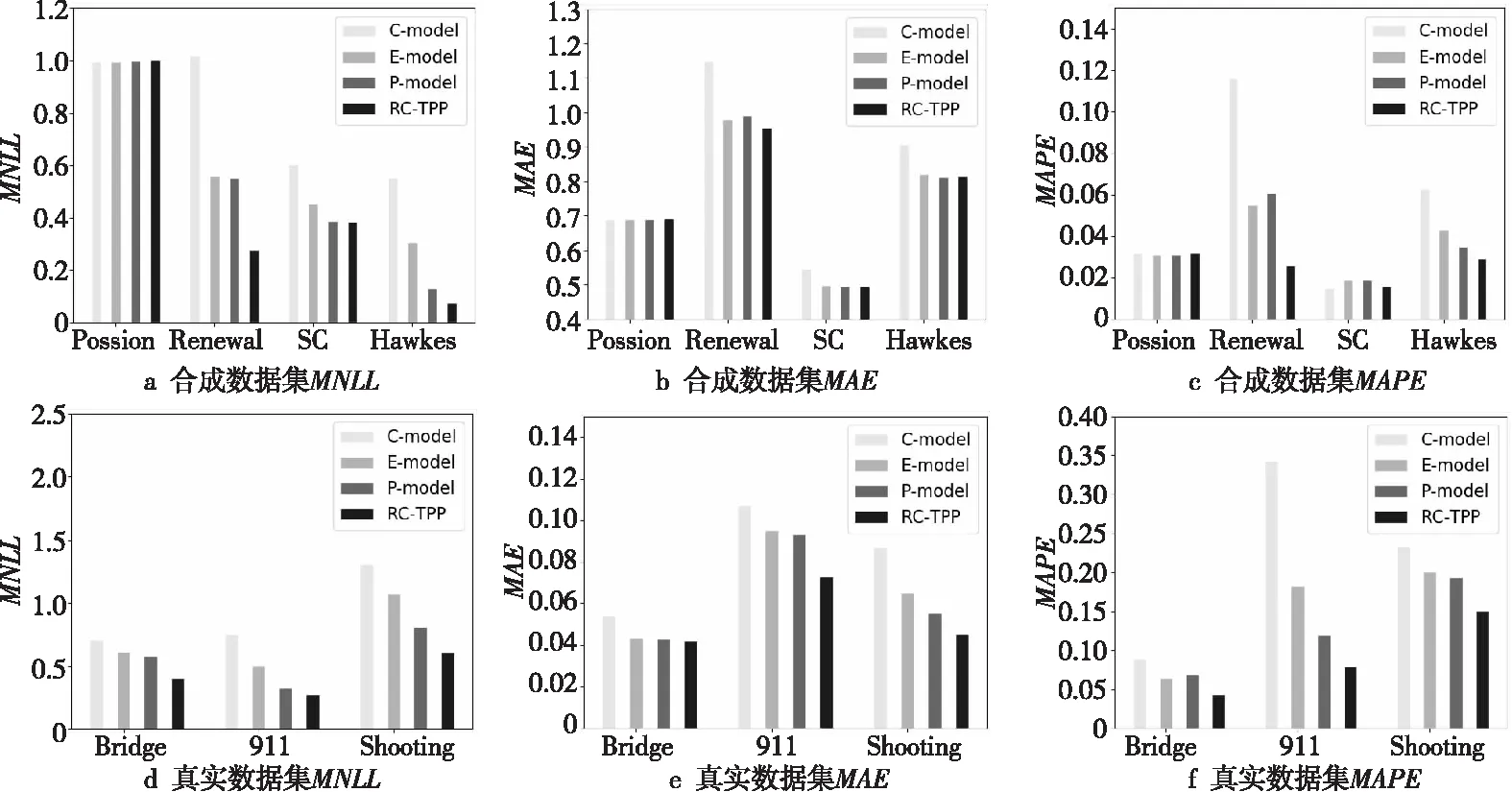
其中,R[t,t+Δ)表示在时间间隔内所有事件的集合,ε表示某事件,Xt={ti|ti p(ti+1|t1,t2,…,ti)= (2) 其中,λ(ti+1|Xti+1)表示在ti+1时刻事件发生的条件强度函数,指数部分表示在[ti,ti+1]期间没有事件发生的概率。时间序列的概率密度函数为: (3) 时间点过程最基本的模型是平稳泊松过程,其假定事件彼此独立且平稳,λ恒定为1;霍克斯过程是另一种经典模型,其条件强度函数依赖于历史事件,是一种自激励点过程模型。 时间点过程模型的条件强度函数是对历史事件的映射函数,是模型的核心。由于递归神经网络具有优越的可学习长时间依赖关系的性能,因此,本文利用递归神经网络来生成条件强度函数。 在事件发生时刻ti,将时间间隔xi=(ti-ti-1)作为递归神经网络的输入,其隐藏状态hi表示如下: hi=f(Whhi-1+Wxxi+bh) (4) 其中,Wh、Wx和bh分别表示RNN的递归权重矩阵、输入权重矩阵和偏置项;f(·)是激活函数。 递归神经网络的隐藏状态可用历史事件向量表示,条件强度函数则表示为最临近事件的运行时间和隐藏状态的函数: (5) (6) 在文献[10,12]中,假设条件强度函数在事件连续发生间隔期间保持不变,式(6)简化为: (7) 此时,基于递归神经网络的时间点过程模型的对数似然函数表示为: lnL({ti})= (8) 由于直接对条件强度函数(即危险函数)建模会影响对数似然函数的计算精度,因此,本文提出基于递归神经网络与累积危险函数的时间点过程预测模型(RC-TPP),通过前馈神经网络对危险函数的积分进行建模,该模型可以得到更准确的预测结果。 Figure 1 Diagram of time series prediction model based on RC-TPP图1 基于RC-TPP的时间序列预测模型框图 基于积分求导法,定义累积危险函数为: (9) 对式(9)求导,得到危险函数: (10) 将式(8)用累积危险函数重新表述为: lnL({ti})= (11) 由于式(8)中包含危险函数的积分,虽然积分可以用数值方法近似计算,但是数值逼近会降低拟合精度,且计算量较大 。而式(11)与式(8)相比减少了积分项,增加了微分项,能够避免对数似然函数中的积分,使预测结果更加精确。 本文所提模型由递归神经网络RNN和全连接网络FCN组成,模型结构如图1所示。其中,Xt-h+1是Xt前面第h个历史事件的集合,Zi(τ)是输出的累积危险函数。 RNN实现对标记事件和历史事件的非线性时间相关性建模;其中,递归层反馈当前时刻的隐藏状态,作为下一时刻的输入。在此,假设RNN在不同时刻共享相同的网络参数。 最后,网络输出累积危险函数,其值为正数,且随τ的增加而增加。将式(9)和式(10)用输出表示如下: Φ(τ|hi)=Zi(τ) (12) (13) RC-TPP预测模型流程如下所示: 输入:历史数据序列X={Xi},时间间隔τ。 输出:累积危险函数Zi(τ)。 步骤1全部样本D←∅; 步骤2 for时刻t(1≤t≤n-1)do: 步骤3生成历史事件序列:S=[X1,X2,…,Xt-1]; 步骤4将(S,τ) 放入样本集D中; 步骤5初始化可学习参数θ; 步骤6从全部样本D中随机抽取批次样本Db; 步骤7优化目标函数,在Db中找到最优参数θ; 步骤8重复步骤6和步骤7,直到迭代达到阈值,得到最优参数θ; 步骤9输出累积危险函数Zi(τ)。 本节首先介绍实验所需数据集,包括合成数据集和真实数据集;然后阐述实验环境及参数设置;最后将本文所提模型与其它基准模型进行对比。实验基于TensorFlow框架进行程序设计,通过下述度量标准来评估序列预测模型的性能: (1)训练损失(Train_loss)和验证损失(Val_loss):评估模型的泛化能力; (2)平均绝对误差MAE(Mean Absolute Error)和平均绝对百分比误差MAPE(Mean Absolute Percentage Error):评估预测精度; (3)平均负对数似然值MNLL(Mean Negative Log Likelihood):由式(11)得出,用于评估预测准确性。 损失函数计算方法如式(14)所示: (14) MAE计算方法如式(15)所示: (15) MAPE计算方法如式(16)所示: (16) MNLL计算方法如式(17)所示: (17) 5.1.1 合成数据集 合成数据集由随机过程生成,表1中列出了4种随机过程;在每种合成数据集中,其中80%的数据作为训练数据,余下的20%作为测试数据。 表1中,Renewal是Poisson的升级版,时间间隔{τi=ti+1-ti|i=1,2,…,n}是相互独立的。在实验中,将霍克斯过程的参数设为:M=1,μ=0.2,α1=0.8,β1=1.0。 对合成数据集进行数据预处理(以平稳泊松过程为例): 首先通过平稳泊松过程生成一组数据,表示事件发生的时间间隔;然后,以事件首次发生的时刻为原点,对生成的时间间隔数据依次累加,得到所需的时间序列(即事件发生的时刻)。 Table 1 Synthetic datasets 5.1.2 真实数据集 实验采用的真实数据集包括: (1)交通拥堵数据集(Bridge):该数据集为2014~2017年美国纽约所有立交桥上发生交通拥堵的统计数据,包括:立交桥名称、位置坐标和拥堵发生的时间等。实验选取拥堵率最高的前10座立交桥进行预测分析。 (2)911报警电话数据集(911):该数据集为2017~2019年美国旧金山警署接到的911电话统计数据,包括:紧急电话(如水电管道故障等)、报警电话和消防火警等事件的报警数量、通话时长和出警时间等。实验选取日紧急电话数及对应部门到达现场所需时间进行预测分析。 (3)枪击案数据(Shooting):该数据集为2013~2018年美国纽约枪击案件的统计数据,包括:枪击案发生的时间、地点、受害人及犯罪嫌疑人等相关信息。实验选取枪击案发生率最高的10处位置进行预测分析。 对真实数据集进行数据预处理(以交通拥堵数据集为例): 首先对数据进行整理和分析,选取拥堵率最高的前10座立交桥;然后对每座立交桥的拥堵时间按照先后顺序排序,计算相邻2次事件之间的时间差;最后,以首次拥堵的时间点为原点,通过累加时间差的方式得到所需的时间序列(即拥堵发生的时刻)。 实验选取3种传统的时间点过程模型与本文提出的RC-TPP模型进行对比,这3种传统模型分别为:常数模型C-model(Constant model)[10]、指数模型E-model(Exponential model)[6]和分段常数模型P-model(Piecewise constant model)[9]。常数模型的危险函数如式(7)所示,指数模型的危险函数如式(6)所示,分段常数模型的危险函数[9]如式(18)所示: (18) Figure 2 Impact of different parameters on performance of RC-TPP model图2 不同参数对RC-TPP模型性能的影响 设4种模型中的递归神经网络有64个单元,全连接网络有2层,每层包括64个神经元。实验采用Adam优化器进行优化[17],设初始学习率为0.001,β1=0.9,β2=0.999,每批数据的大小为256。 实验结果由负对数似然函数-logp*(ti+1|t1,t2,…,ti)来评估,采用每组测试数据的负对数似然函数的均值作为最终的平均负对数似然值,其值越小,说明模型的拟合效果越好。 5.3.1 不同参数对性能的影响 针对RC-TPP模型中不同的超参数对性能的影响进行分析,分别进行了训练批次大小、递归神经网络截断深度、递归神经网络单元数目、全连接网络深度和全连接网络单元数目等5个方面的对比实验,结果如图2所示。图2a中,当训练批次大小逐渐增加时,MAPE下降明显;当批次大小超过64后,MAPE并未发生显著变化;然而,随着训练批次大小的增加,训练难度也随之增加,因此,得出训练批次大小为64时,本文设计的模型可以达到最优的预测性能。同理,经实验验证依次得出,当RNN深度达到10层时(图2b)、RNN单元数目为32时(图2c)、FCN深度为2层时(图2d)、FCN单元数目为64时(图2e),RC-TPP模型的预测性能最优。 5.3.2 4种模型的性能对比 表2和表3分别列出了4种模型的训练损失(Train_loss)和验证损失(Val_loss)、平均绝对误差(MAE)、平均绝对百分比误差(MAPE)和平均负对数似然值(MNLL)等性能指标的对比结果。 由表2可看出,对于MAE评价指标,4种模型表现的性能近似,但RC-TPP模型略优于其它模型;对于MAPE评价指标,4种模型在平稳泊松过程和自校正过程中的表现近乎一致,但在平稳更新过程和霍克斯过程中,RC-TPP模型具有较大优势;对于MNLL评价指标,4种模型在平稳泊松过程中性能相近,而在其它3种数据集上,RC-TPP的性能最突出。综上,在合成数据集的实验中,本文RC-TPP模型的各项性能评价指标均优于其它模型的,预测效果更好。 由表3可看出,在真实复杂的数据集上,RC-TPP模型的各项性能评价指标的优势更加明显,这是因为真实数据比合成数据更复杂,而RC-TPP可以更好地应变并拟合真实数据的复杂特征。其中,RC-TPP模型的MNLL比其它模型的减小了至少17%,MNLL越小,即代表模型预测的精度越高。此外,RC-TPP模型的MAE和MAPE也均比其它模型的显著减小,误差值越小,表示预测效果越好。与此同时,RC-TPP模型的Train_loss和Val_loss也均小于其它模型的,即泛化性能更好。 Table 2 Experimental results on synthetic datasets Table 3 Experimental results on real datasets Figure 3 Performance comparison图3 性能对比图 图3所示为在合成数据集和真实数据集上的性能对比结果,可以更直观地看到,在合成数据集上,RC-TPP模型的MNLL、MAE和MAPE均低于其它模型的,预测效果更好。在真实数据集上RC-TPP模型的MNLL、MAE和MAPE均远低于其它模型的,即RC-TPP模型更能胜任复杂的真实事件的预测任务,预测精度更高,时间复杂度更低。 本文提出了基于递归神经网络和累积危险函数的时间序列预测模型,即从历史事件的数据中挖掘出可用于预测事件未来发展趋势的信息。首先,基于积分求导法,设计条件强度函数式,提高序列预测精度。其次,构建基于递归神经网络和累积危险函数的时间点过程模型;通过递归神经网络捕获历史事件的非线性依赖关系,利用全连接网络获得累积危险函数。最后,选择具有代表性的合成数据集和真实数据集进行性能对比分析。实验结果表明,本文设计的模型可以更好地进行城市事件的时间序列预测,效果优于其它模型。 在未来工作中,本文提出的模型可用于诊断分析[18,19],以提高预测的精度;此外,还可以进一步结合影响事件发生的上下文信息,如地图图像、社会/交通事件描述等,从而更加全面准确地预测城市中发生的异构事件,为有关部门提供政策调控依据及决策支撑。
3.2 基于神经网络的时间点过程





4 基于RC-TPP的时间序列预测模型
4.1 累积危险函数
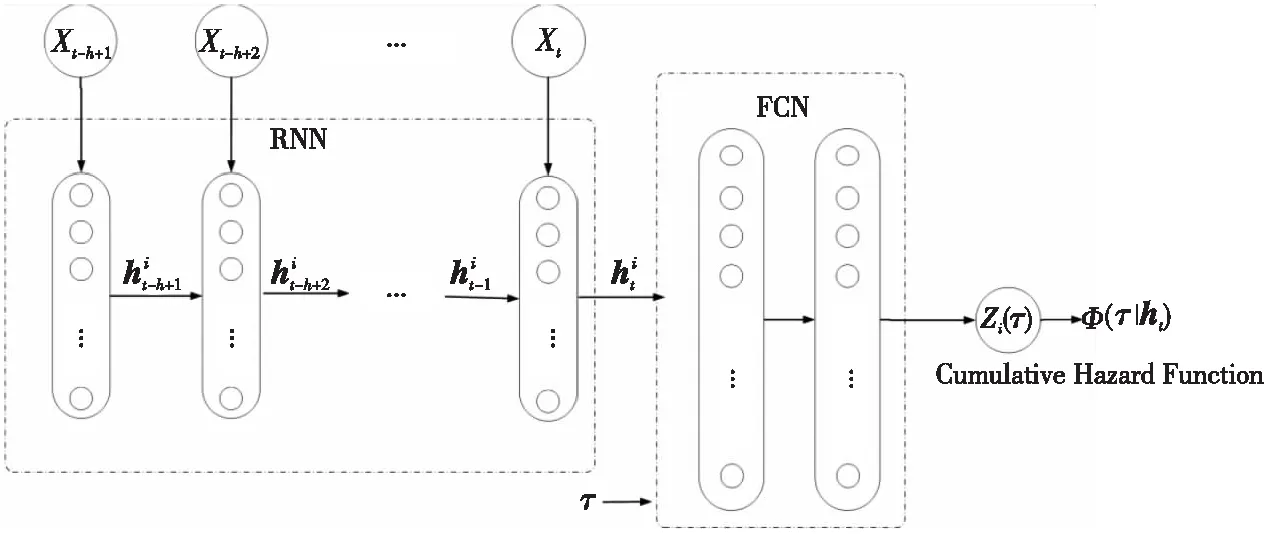


4.2 模型结构
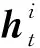
4.3 RC-TPP预测模型
5 实验分析
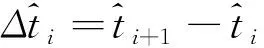
5.1 实验数据

5.2 实验环境

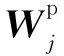
5.3 实验结果
6 结束语

