竖井联系测量及精度分析

林川 钟世彬

（1.江西省测绘成果质量监督检验测试中心 江西南昌 330009；2.江西省自然资源档案馆 江西南昌 330046）

1 引言

地下工程的施工及地下矿山的开采，为了解决巷道的设计施工及其他问题，必须知道地面和井下的相对位置关系。同样，井下各水平方向上的测量，都须采用同一坐标系。因此，如何将井上的平面位置与高程正确地传递到井下，使得井上、井下之间建立相关联系。建立这种联系的测量方法有竖井联系三角测量、竖直导线等等，而竖井联系三角测量，可将地面已有控制点的位置和高程精确地传递到地下，从而建立地面、地下统一且相同基准中，为地下控制测量提供依据。竖井联系测量包括平面位置测量和高程测量传递，在实际工程中，应根据具体工况、精度要求进行灵活，合理的选择。此文章主要阐述联系三角形的方法与原理，精度评定及影响精度的因素。

2 竖井联系三角形测量

2.1竖井联系三角形测量方法、原理

竖井联系三角形测量[1]方法是一种较成熟的几何定向方法，通过构造、优化竖井联系三角形形状，利用高精度测量装备，两者结合起来可达到所要求的精度。

如图1所示，在井口固定框架，悬挂两根钢丝O1，O2，并在底部悬挂垂球，使垂球浸入水桶中，但不能接触水桶，使其稳定并保持铅垂线方向，而O1，O2起到了传递坐标的作用。

图1 竖井联系三角测量示意图

在实际测量操作过程为：在地面点A（近井点）设站，并与已知控制点D后视，得到观测α角及连接角ω，并丈量三角形边长a，b，c，在地下控制点A1安置经纬仪观测ω1及α1其角，并丈量地下联系三角形边长a1、b1及c1。

2.2几何精度评定

如图2所示，由已知地面及地下联系三角形α，ω及α1，ω1，则地下控制边A1D1的坐标方位角为:

图2 联系三角形法投影示意图

式(1)中，αAD为已知地面控制点A、D方位角。通过联系三角形可求得β＋和β1，在三角形ABC和A1BC中：

三角形ABC和A1BC这两个联系三角形中，只观测了二条边，一个内角，从而有一个多余观测分量[2]，可按边角网进行条件平差，即可得到各观测量的最佳值。地面、地下两个联系三角形的平差模型为:

对式(3)微分可得：

其中α、α1均很小，则cosα≈1，则c-b≈a，式(4)简化为：

则误差方程式为：

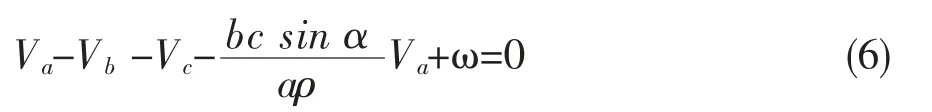
各观测值的权为：

其中ms为量中误差，ma=mb=mc=ms，m为测角中误差。

则方程为：

各观测值的改正数Vi可由式（10）求得：

求得各观测值的改正数，并求得改正后的观测值，代入式（2）计算β和β1，由式(1)求得地下控制边的坐标方位角。依据地面上直接丈量的边长a,b,c和观测角ω，α求得吊垂线的方位角时，得到αCB=αAD+(ω+α+β)-2×180°。

2.3影响精度的因素分析

由公式αCB=αAD+(ω+α+β)-2×180°可看出，当αAD和ω，α观测精度确定以后，推算角β角的精度影响CB边的方向精度，而β角是由联系三角形解算求得，所以，β角的精度取决于联系三角形的形状，以下对影响β角精度的因素进行分析[3]。

在实际边长丈量操作中，都是采经过检定合格的钢尺进行，并且丈量边长较短，可认为：ma=mb=mc=ms，代入式(11)，可得：

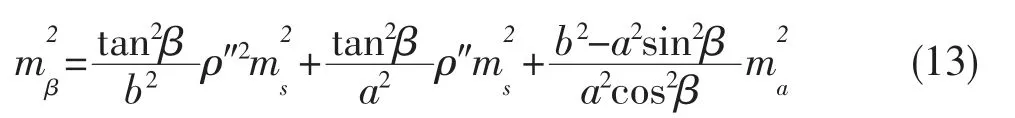
故中误差方程可写成公式（14）：

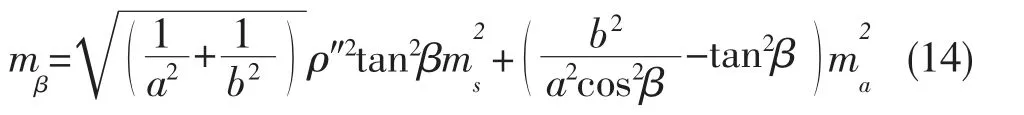
由式(14)可知，β角推算精度受观测角误差、观测边误差影响，同时联系三角形形状对其也存在很大影响。以下分别对三方面影响因素分别讨论。

2.3.1由测角观测误差讨论联系三角形的形状

由式(14)可看出，角度α的观测误差对β角精度影响为：

①β角越小越好，当β≤2°时，有：

cos2β≈1 tan2β≈0

2.3.2由边长观测误差来讨论联系三角形的形状

由式(14)中可知边长观测误差对β角精度影响为：

对式(17)进行微分，并写成中误差的形式得：

式(18)中所包含的因素可知：影响β角精度的因素有两个，一个为测角误差的影响，另一个为量边误差的影响。前面也假定过的ms=ma=mb，式（18）可写成：

2.4综合分析联系三角形的形状

经综合分析，考虑地下导线起始方向角的误差，可用式(20)表示:

式中:m(α)s为测边误差引起的角度误差;m(α)β为测角误差，其中mαAD可不考虑。

①对于m(α)s，包括地面、地下边长丈量误差引起的角度误差，当联系三角形相似且ma=ma1，mb=mb1，mc=mc1，均为ms时，有：

改进算法可写成：

②对于m(α)β，包括地面上、地下的角度观测误差mα和mα1。实际操作中，地面、地下两个联系三角形都操作成相似三角形，因此，由方位角的推算公式可知，观测角误差对定向精度的影响为：

一般认为地下方向测量误差mα1为地面方向测量误差mα的1.5倍，所以上式可以写成：

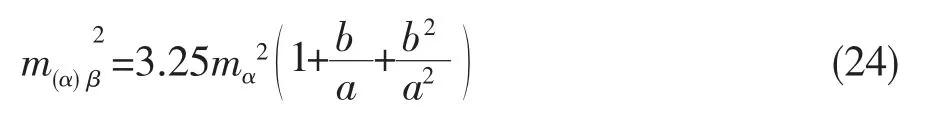
3 数据处理分析

3.1数据观测及处理分析

以表1数据为该工程进行的对称三角形联系测量，为了提高精度，缩短定向的时间，通常悬挂三根钢丝，构成双联系三角形。具体数据见表1。

3.2计算结果与分析

由表1数据计算结果可知，影响联系三角形测量的主要因素是比值b/a和推算角β观测精度，具体分析结果如下[5]：

(1)联系三角形中的α，α1，β，β1角度布设越小越好；

(3)联系三角形的形状宜考虑选择狭长的延伸三角形，可减少量边误差对传递角的影响，且在角度传递过程中，宜选择小角β和β1作为传递方位路线；

(4)尽可能增大两悬吊垂线距离。

表1 联系三角形计算表

4 结束语

随着科学技术的发展，解决地下工程施工过程中，地上与地下相关位置问题的方法也越来越多，本文以某地下工程项目为实例，论述了联系三角形测量方法在地下工程施工过程中的实用性、可操作性，并分析总结了影响联系三角测量精度的因素，从而在现实操作中提高精度与效率。