基于Adams圆弧摇杆摇椅倾覆性研究

■陈于书，赵汉伟

(南京林业大学家居与工业设计学院，江苏南京 210037）

摇椅的稳定性与摇杆结构有着密切的关系。摇杆的设计在保障摇椅使用过程中舒适性的同时，也要做到安全可靠，确保使用过程中不会发生倾覆。本文以最常见的圆弧摇杆摇椅为例来分析摇椅摇杆与其倾覆性关系。

1 研究过程与方法

1.1 模型的选取

摇杆作为摇椅实现摇摆功能的核心部件，在摇椅的使用过程中发挥着重要的作用[1-3]。本研究通过文献资料、卖场、网络的方式总共搜集摇椅225件，其中有65%的摇杆都可以用圆弧进行拟合[4-5]（图1）。这表明圆弧摇杆作为最普遍的摇杆形式，被广泛运用到摇椅的设计中并对摇椅摇杆的设计具有重要的参考意义[6]。

图1 圆弧拟合摇杆

1.2 摇椅倾覆性理论分析

在尽可能简化摇椅模型后，同时参考国标对摇椅稳定性检测依据，对圆弧摇杆摇椅使用过程中所处的状态进行理论分析。具体步骤如下。

1.2.1 确定圆弧摇杆摇椅的倾覆极限

简化摇椅模型在使用过程中摇椅与人始终保持相对静止，即质心G相对摇椅不发生位移变化，同时质心G在摇杆的作用下一起摆动。摇杆与地面PP'始终保持相切状态[7]。当摇杆后端A，与地面相切时运动至A2点，摇椅仍处于安全状态，随后在外力的作用下，摇椅将绕A2点做圆周运动，至A1G垂直于地面时，摇杆达到最大后倾程度，此时摇椅若再受到外力，摇椅便会向后倾覆[8]。同理，当摇椅前倾时，至摇杆前端B运动至地面相切B4处，在外力的作用下摇椅将绕B4点做圆周运动，至B5G垂直于地面时，摇椅处于前倾最大极限（图2）。

图2 圆弧摇杆摇椅质心极限运动轨迹简图

1.2.2 圆弧摇杆摇椅倾覆分析

摇椅稳定性检测依据国标GBT-10357.8-2015《家具力学性能实验-第8部分》，在椅座上加载8个质量为10kg，直径350mm，厚度48mm的加载盘，在实验过程中加载盘与摇椅不发生相对位移。实验要求使摇椅尽量前倾，或直至椅背支撑表面与水平面垂直。在重力作用下，使摇椅自由向后摇，记录椅子是否倾翻[9]。

圆弧摇杆尽量前倾，使得此时的质心G与摇杆前端B的连线尽可能垂直于地面，在此状态下放开摇椅，让摇椅在重力的作用下自然向后倒下，这个过程中摇椅的重力势能转化为摇椅的动能。当质心G与摇杆的曲率半径R的圆心O的连线垂直于地面时，即重心G运动至最低点位置时，摇椅的整体势能达到最小且动能最大，此时摇椅将动能转化为势能。直至将摇椅的全部动能转化为摇椅的势能，摇椅达到检测状态下的最大后倾程度。若此时的后倾程度小于摇杆的后倾极限，则摇椅处于安全状态。

要满足摇椅处于安全状态，则圆弧摇杆的摇椅在使用过程中，质心G距离摇杆后端A的距离不小于质心G到前端B的距离，即GA≥GB，摇椅处于安全状态。此时摇椅整体质心G的安全位置处于摇杆对应弧度的角平分线或AB中垂线的前侧部分。

1.2.3 圆弧摇杆倾覆性理论推导

建立简化的摇椅模型后，主要包含5个部件，后腿部件、椅背部件、坐面部件、前腿部件、以及摇杆部件。从侧面看其质心分布如图所示。以后腿与摇杆接触点N作为为坐标原点同时两腿与摇杆的连线作为X轴建立直角坐标系（图3）。

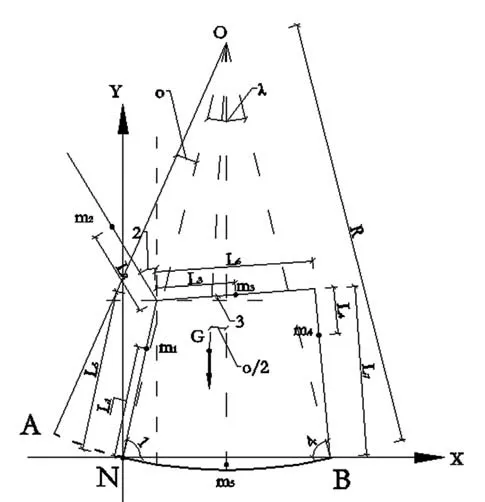
图3 圆弧摇杆安全尺寸确定

摇杆与摇椅结合后，摇椅的质心G的坐可以利用力矩合成法进行求解。

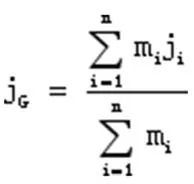
式中，jG表示合质心在某一坐标轴上的坐标；i表示各个部件；n表示部件数量；j表示某个部件质心对应的x、y、z（本文仅讨论摇椅侧面，故不讨论z轴）轴坐标；m表示部件质量。求解的此时摇椅的质心横纵坐标为：

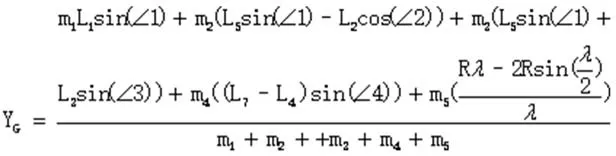
此时的质心G位于摇杆NB上部，偏离∠NOB角平分线的角为∠o/2，利用三角函数关系可以求解出其大小如下。

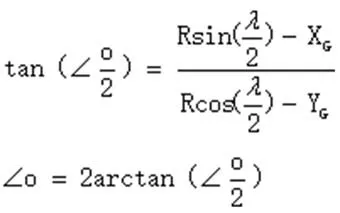
要保证摇椅在摇摆过程不会发生倾覆，摇椅质心应处于摇杆对应弧度的角平分线处处为此可以求出，圆弧摇杆A到N点至少需要延长∠o的弧度。

同时若摇椅椅腿与摇杆前端的连接点不在摇杆最前端B点，则摇杆前端B点到椅腿前端结合点对应的弧度也应在摇杆尾部得到相应的延伸。

1.3 基于Adams的圆弧摇杆摇椅倾覆性实验

1.3.1 模型建立与导入

在SolidWorks中建立简化后的圆弧摇杆摇椅。同时将摇椅的材质设置为相同材质，其密度取0.8g/cm3。按照国家检测标准，在摇椅上方放置8个质量为10kg直径为350mm厚度为48mm的加载盘。我们将其简化为直径为350mm高度为384mm斜圆柱，使得圆柱母线紧贴摇椅靠背，同时定义斜圆柱体质量为80kg。

运用SolidWorks中建好模型后，将模型保存为Adams所需要的格式，通常使用后缀为.x_t的格式[10-11]。而后在Adams中模型导入后，会显示模型的质心，而后将模型经过旋转，调整至检验状态，使摇椅尽可能前倾，即使得模型的质心与摇杆前端接触点的连线尽可能垂直于地面[12]。

1.3.2 理论质心计算

通过用SolidWorks建立摇椅模型，可以在软件中快速求解摇椅质心。为验证公式的正确性，通过确定模型参数来计算实验模型质心[13]。实验模型的摇杆截面为40mm×40mm，中心弧长为417mm；前后椅腿截面为30mm×40mm，后腿中心线长301mm且与水平里面夹角成67°，前腿中心线长为313mm且与水平面成72°；坐面简化为厚度为20mm的板件，坐宽为600mm，坐深直线为398mm，与水平面成10°；靠背厚度为20mm，靠背宽度为600mm，靠背高度中线为419mm与垂直面成30°。取摇椅用材为，0.8g/cm3。

简化后的模型除摇杆外其他零部件的质心可以大致看成在零部件中心线的中点上。运用CAD软件，以摇椅后腿与摇杆的结合处为原点建立直角坐标系，求出各零部件的质心位置坐标[14]。将所有参数带入公式，解得质心横坐标XG为97.39，纵坐标YG为312.94，同样在SolidWorks中直接求出质心坐标，XG为97.45,YG为313.35（图4）。几乎无差别，证明圆弧摇杆摇椅质心求解公式可靠。带入公式解得无载荷情况下∠o为11.53°，80kg载荷后∠o为12.23°。

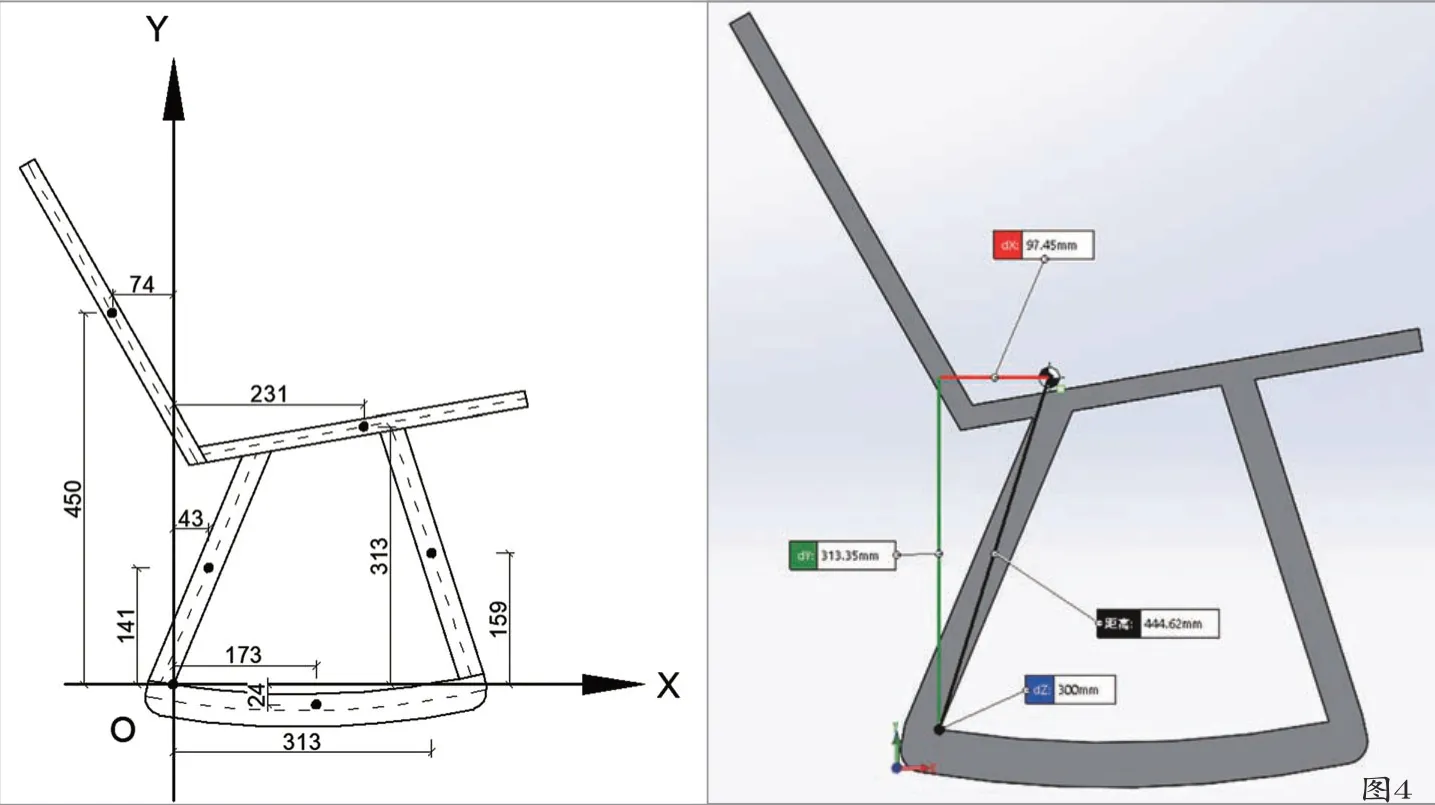
图4 摇椅理论质心与模型质心求解对比

1.3.3 模型实验模拟

在Adams中建创建“地面”，为保证实验的准确性，调整“地面”与摇椅前端接触点恰好接触。同时用固定副将“地面”固定。

在摇椅倾覆模拟实验中选取六组模型分别为：摇杆的情况分为三种情况，摇杆与摇椅腿部恰好结合、摇杆延长至摇椅质心的安全位置、摇杆延长至摇椅载荷检验质心安全位置；以及摇椅是否有载荷的两种情况。

2 结果与分析

在上述基础上，将SolidWorks建立好的摇椅模型导入Adams中，利用ADAMS/View的测量和仿真输出功能对上述结果进行研究分析。模拟摇椅在尽可能前倾的情况下分析其运动状态，及记录摇椅质心运动轨迹。如图5所示，图中白色为摇椅主体部分，曲线表示摇椅的总质心运动轨迹，蓝色表示国标中施加的80kg载荷。从实验表现来看，在圆弧摇杆摇椅试验中，当实验步数设置为1500时，摇杆与椅腿两端连接时，有无载荷，在检测条件下，摇椅都会发生倾覆；当将摇杆延长至摇椅自身重心的安全位置时，有载荷会发生倾覆，无载荷情况下不会发生倾覆；当摇杆延长至载荷重心安全位置时无论是否加入载荷摇椅都不会发生倾覆。

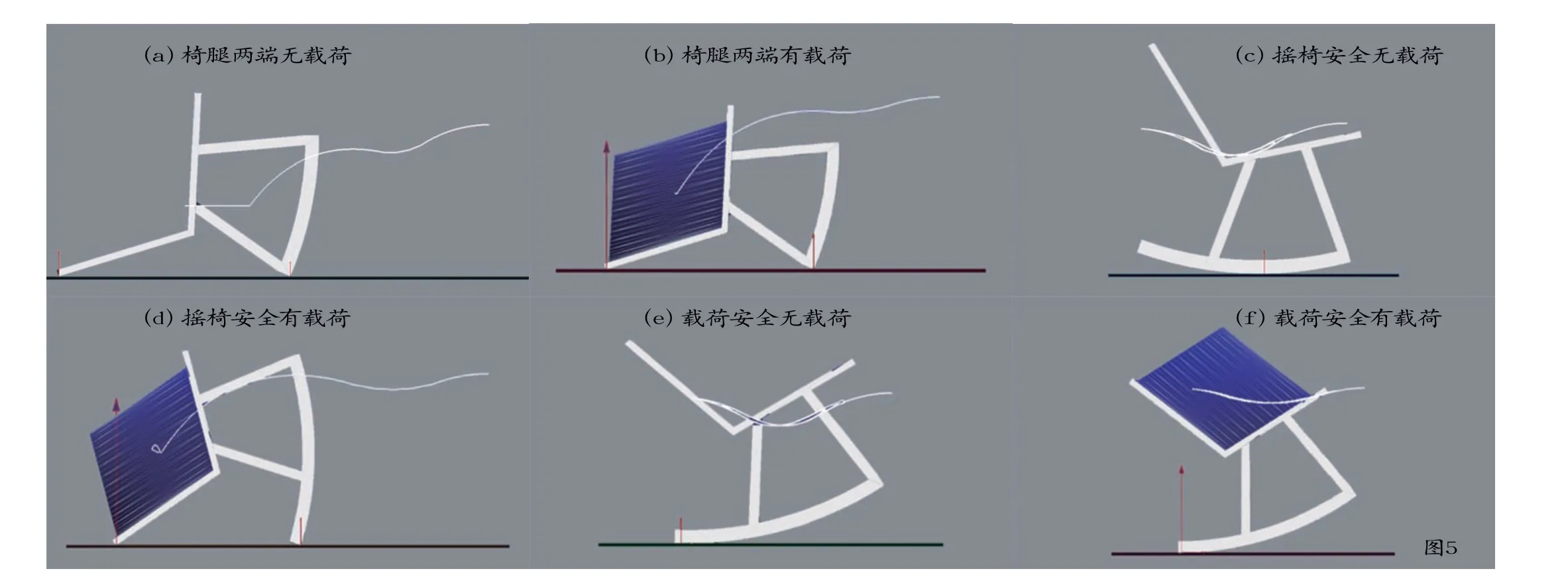
图5 摇椅不同状态下的质心运动轨迹

通过实验模拟，可以得知理论公式求摇椅安全角基本符合摇椅的实验结果。圆弧摇杆的稳定性受到摇椅载荷的影响，设计过程中许用载荷越大，摇杆需要延长的越多。

为进一步形成对比分析，将摇椅的质心高度与时间的对应关系进行统计分析，三组实验质心高度变化曲线表明，由于实验过程摩擦力的存在，无论摇椅是否发生倾覆，在检测开始时摇椅质心具有最大高度，而后衰减。摇椅在不发生倾覆的情况下，摇摆过程中质心高度呈现衰减的正弦曲线。

3 结语

通过质心理论公式推导和计算机仿真模拟验证，证明摇椅质心与圆弧摇杆的关系与理论公式推导一致。即设计摇椅的过程中使得摇椅载荷后的整体质心G处于圆弧摇杆对应圆弧的角平分线前端，在合理使用摇椅过程中便不会发生倾覆。相比于传统方法，通过摇椅检测实物检测摇椅倾覆性，运用圆弧摇杆的倾覆公式计算能有效缩短摇椅设计周期和提升摇椅设计的合理性。