一种谐波数据存储及责任评估方法

吴 俊，楼伯良，黄弘扬，马智泉，李 培，徐群伟，吕文韬

（国网浙江省电力有限公司电力科学研究院，杭州 310014）

0 引言

近年来，随着新能源发电、高压直流输电等技术的发展和应用，使得电网中大量使用电力电子器件构成的设备，这些设备成为新的谐波源且威胁系统安全运行[1-5]。

谐波责任划分是谐波治理的基础，然而现有的电力系统谐波监测终端覆盖面较小，主要分布于主网母线中，以浙江电网为例，谐波平台接入谐波装置不超过5 000 台，因此难以支撑覆盖全省的谐波责任划分。另外，用电负荷需求不断增加促使电网容量和节点相应增加，使得当前电网已呈现大电网特性，导致现有基于关系型数据库设计的谐波系统已显现运算瓶颈。

图论是一种非常适合处理电力系统复杂拓扑的技术，因此已在电力系统中得到广泛应用。文献[6]建立了交流场等效模型并基于图论求解模型，实现了交流场最后断路器快速、准确、智能的判断，文献[7]采用基于图论的输电线路功率组成的快分析方法完成关键输电断面快速搜索，文献[8]引入图论中最小生长树的理论以准确确定故障区段边界实现不接地故障定位。然而鲜有文献将图论应用于谐波计算中。

近年来，国内外学者在谐波状态评估和谐波责任划领域开展较多研究，文献[9]提出了谐波状态估计分层算法，文献[10]研究了误差不确定性对谐波状态估计的影响。文献[11]利用M 估计稳健回归法开展多谐波源责任划分，文献[12]提出以谐波电流中快速变化分量为工具抽取出各谐波源节点与关注母线间的谐波阻抗并计算谐波责任，文献[13]基于稳健回归开展谐波发射水平的研究。然而以上研究少有利用谐波状态评估结果开展谐波责任评估。

针对以上问题，本文首次将图数据库应用于谐波数据存储和计算，进一步的为实现谐波状态评估给出网络节点导纳计算方法并采用信赖域进行模型求解。然后，构建评价谐波责任划分的指标-谐波贡献度。最后，在多种线路规模下比对图数据库与关系数据库的计算速度，并在浙江电网某220 kV 变电站拓扑中开展谐波评估及谐波责任划分仿真验证。

1 基于图论的系统谐波数据存储与运算

1.1 基于图数据库的电网谐波数据存储

图论可为复杂的网络建模及计算提供有效支撑，且已被验证可显著提高复杂网络的计算性能。

在图论中，可以将系统网络建模为图，即G（V，E），其中顶点V={v1，v2，…，vn}表示网络对象，而边E={eij}用于描述对象vi和vj之间的关系。

以电力系统中母线、支线及设备的连接关系为基础，可利用图论直观的表述电力系统。具体来说，可将电力系统各部分映射为顶点和边，顶点指发电机、负载、变换器等对象，而线路、变压器、隔离开关等连接部件则可视为边。图1 是某个电力系统实际拓扑信息，图2 则是利用图论构建的关系。

图1 某系统拓扑结构

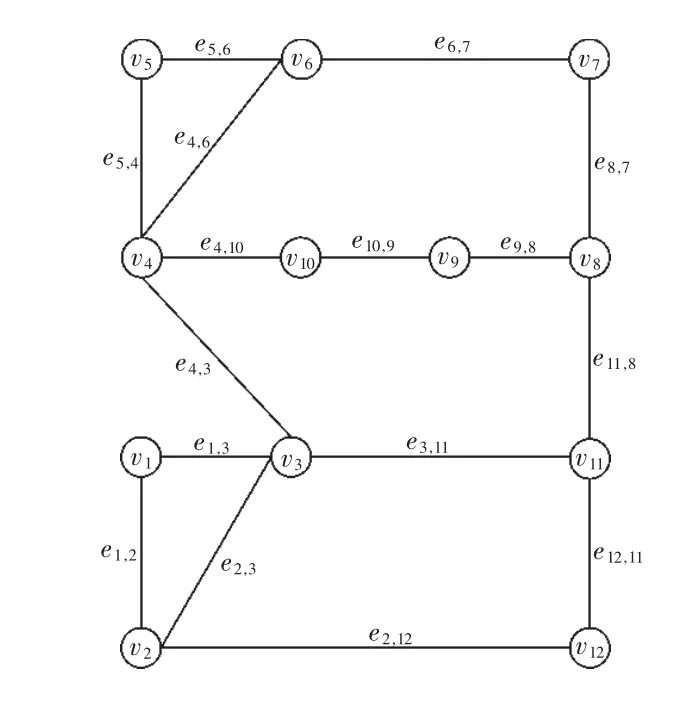
图2 图论转换后拓扑

相比于传统的关系型数据库，基于图论可更直观、简洁表示整个系统谐波信息，例如：无需分别构建母线表、分支线表等再利用中间表建立母线和分支线的关系。为实现基于图论的谐波数据存储，顶点中需要存储顶点id、顶点名称、顶点类型、谐波等数据，谐波数据则包括各次谐波电压（电流）幅值及相角、有功、无功等；边则存储所连接的起始顶点id、线路电阻、线路电抗，对地电容等。

1.2 基于图论的数据运算

基于图论计算设计的数据库中由于每个顶点都可以使用来自身及其邻居的信息独立计算，因此实质上是将一个问题分解为较小的子问题，使得计算灵活且有效。

以实现Ax=b 为例，其对应的矩阵为：

映射到图论数据库中开展计算时，其效果如图3 所示。

图3 基于图论的计算

2 谐波状态评估模型

2.1 网络节点导纳

2.1.1 线路阻抗

线路导纳为阻抗Zl（如式（1）所示）和对地导纳B 的一半，基波与各次谐波模型独立计算。

基波与谐波的线路模型差异如图4 和图5 所示，各次谐波模型计算时，线路电抗X 值需要乘以该次谐波阶数，对地导纳同样如此。

图4 线路基波阻抗

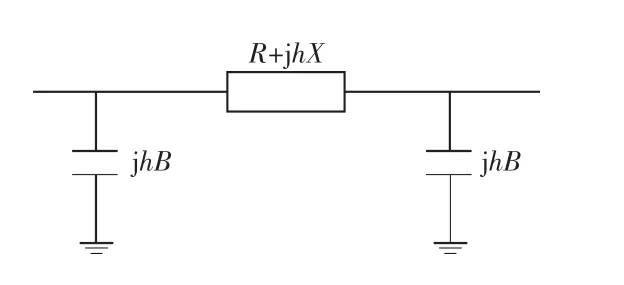
图5 线路谐波阻抗

根据Yl=1/Zl可以计算线路基波导纳，谐波模型中线路导纳同样以该公式进行计算。

2.1.2 节点自阻抗

谐波模型中需要将基波潮流中的线性PQ 负荷（即该节点的谐波电流幅值表现为0）数据转化为该PQ 节点的谐波阻抗模型，转化后如图6 所示，各次谐波模型计算时，电抗X 值需要乘以该次谐波阶数。同样通过Y=1/Z 计算该节点的谐波自阻抗。

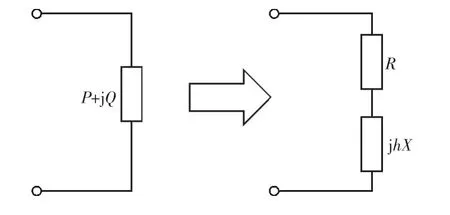
图6 PQ 负荷的谐波阻抗转化示意

2.1.3 网络节点导纳矩阵

以图7 所示的简单3 节点系统为例，假设某次谐波的相应支路导纳与节点自导纳分别如表1，2 所示，节点导纳矩阵Y 是一个n×n 阶矩阵，其对角线元素Yii等于与该节点相连的所有线路导纳、线路对地导纳一半、以及该节点的自导纳之和，非对角线元素Yij等于连接节点i，j 间的支路导纳的负值。

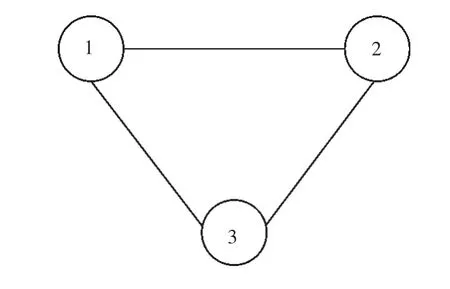
图7 3 节点系统

表1 3 节点系统的线路参数

表2 3 节点系统节点参数

2.2 节点谐波状态评估模型

以图7 所示的3 节点系统某次谐波为例，假设节点1，2 为已有谐波测量节点，3 为未测量节点。将网络节点导纳矩阵Y、网络中测量谐波节点电压向量、有功、无功代入式（2）、式（3）计算：

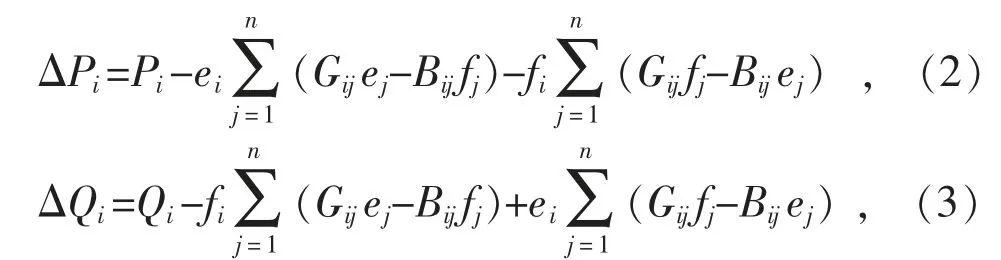
式中：Vi=ei+jfi，即ei表示电压幅值乘以电压相角的cos（）函数值，fi则是电压幅值乘以电压相角的sin（）函数值；Yij=Gij+jBij，分别是导纳和阻抗。

而状态估计模型如式（4）所示，令f（x）的值在求解域中最小的x 即为待求值。

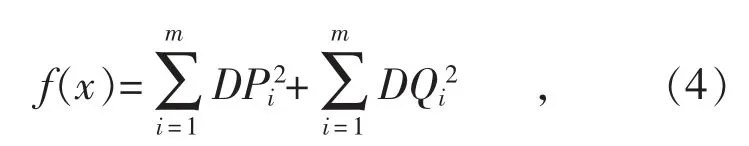
式中：DPi，DQi分别代表已测节点i 的谐波有功、无功平衡。

2.2.1 模型求解

本文使用信赖域求解式（4），信赖域算法的基本思想在当前迭代点xk给定一个信赖域半径hk（hk＞0），在xk为中心hk为半径内以一个二次模型逼近目标函数f（x），并以二次模型在xk的信赖域内的极小值点作为下一个迭代点[14]。

信赖域的数学模型如式（5）所示，是目标函数在极值点的一个近似二次函数：

式中：gk为目标函数f（x）在当前迭代点xk的梯度；Dk为f（x）在xk处Hesse 阵▽2f（xk）；hk为第k 次迭代的信赖域半径。

目标函数f（x）在第k 步的实际下降量Ark与信赖域模型的预测下降量Prk分别见式（6）、式（7），评价函数rk为：

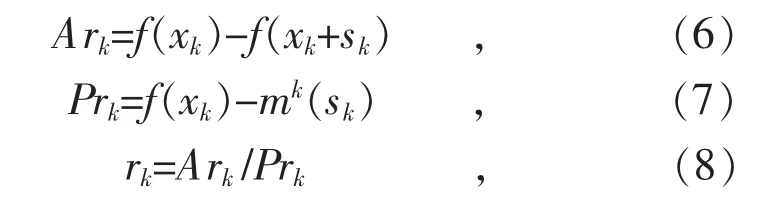
式中：sk=xk+1-xk为某次迭代的步长。

rk一方面衡量信赖域模型与目标函数的逼近程度，当rk>0 时，说明与优化目标一致，函数值呈下降趋势变化，试探步长可以接受，当rk<0时，则说明与求解目标相反，该步试探步长需舍弃。另一方面rk可用于确定下次迭代的信赖域半径，一般地，若rk接近于1，接近程度良好，可增大信赖域半径；若rk接近于0，则缩小信赖域半径；若rk位于（0，1）之间，不接近区间边界，可保持信赖域半径不变。

2.3 谐波责任评估

2.2节中实现了各节点谐波状态评估，其本质上是求取了系统整体叠加到该节点的谐波。然而开展谐波责任划分需量化系统中其他节点对该节点的谐波影响情况。因此，本文以谐波状态评估值为基础，通过谐波潮流量化评估其他节点对某个节点的谐波贡献情况。

首先，计算出的某次网络节点电压向量Vi与网络该次节点导纳矩阵Y 作为输入。

网络的谐波潮流计算公式可以写为：

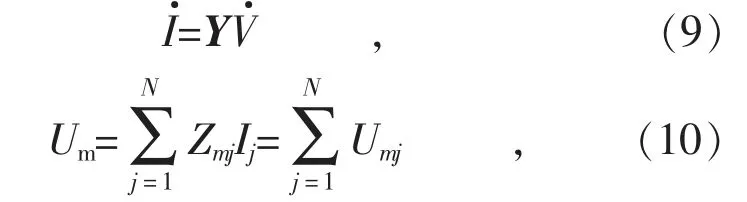
式中：Zmj为节点m 与j（m，j=1，2，…，N）之间的谐波互阻抗（m≠j）或自阻抗（m=j）；节点阻抗矩阵Z 是节点导纳矩阵的逆。以关注节点m 的谐波电压相量为参考，网络中其他谐波源j 对该节点的谐波贡献度指标定义为：

3 验证

3.1 图数据库验证

为验证图论在处理电网模型高效性，本文构建了在6 000 条线路、12 000 线路、24 000 条路、36 000 条线路的工况下，分别在关系型数据库oracle 及图数据平台TigerGraph 的运算，其运算情况如图8 所示。

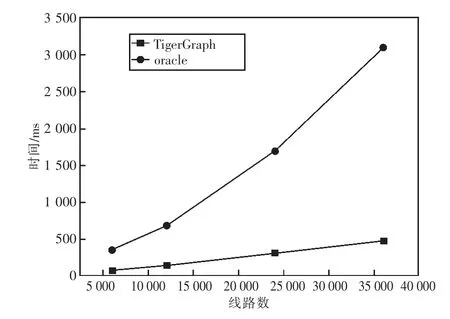
图8 不同数据库运算效率比对

从图8 可以看出：随着线路规模的增大，基于图平台的运算效率显著优于关系型数据库。在6 000 条规模时oracle 下的运算时间是TigerGraph的4.11，而在36 000 条时则达到6.42 倍。

3.2 谐波责任验证

本文以某220 kV 变电站拓扑为对象，共计26 个测点，如图9 所示，包含10 个未测点及16个测试点。文献[15]已对基于信赖域进行谐波状态给出了算例说明，本文不再赘述。应用图论处理后，其拓扑如图10 所示。

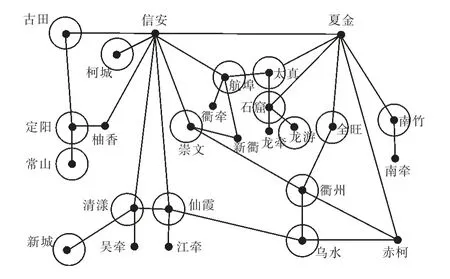
图9 某220 kV 变电站拓扑

图10 基于图论表示的某220 kV 变电站拓扑

以非谐波源节点1（常山）为关注节点，谐波源节点5，7，20，21，22，23 对其谐波贡献度如表3 所示，其中节点7 和20 谐波贡献度最大，但节点5，21 及22 则相近。

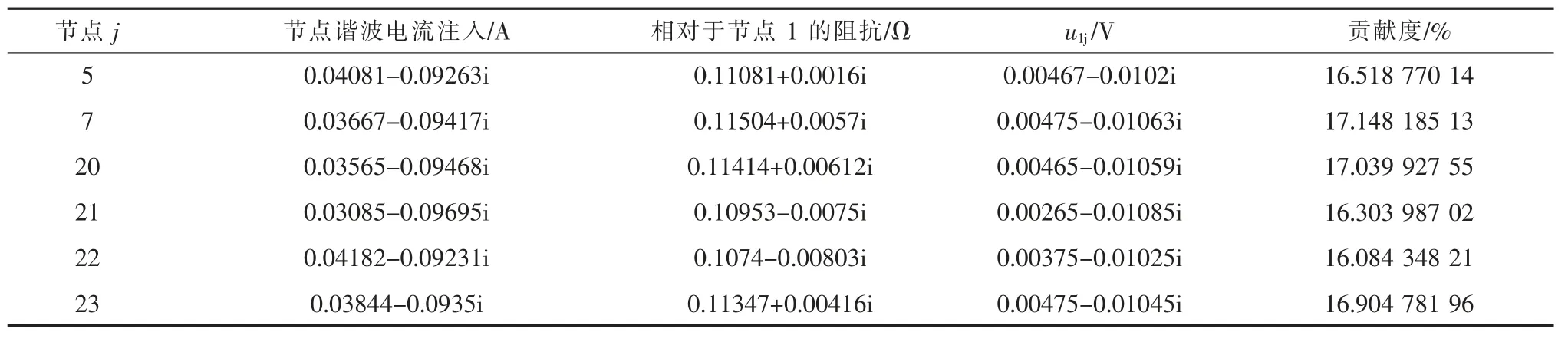
表3 节点1 谐波贡献度

以谐波源节点为例，如以节点5（吴牵）为关注节点，谐波源节点5，7，20，21，22，23 对其谐波贡献度如表4 所示，从该表数据来看，对于节点5 来说，节点23 贡献度较大，而节点7 和20 次之，节点21 和22 稍小。

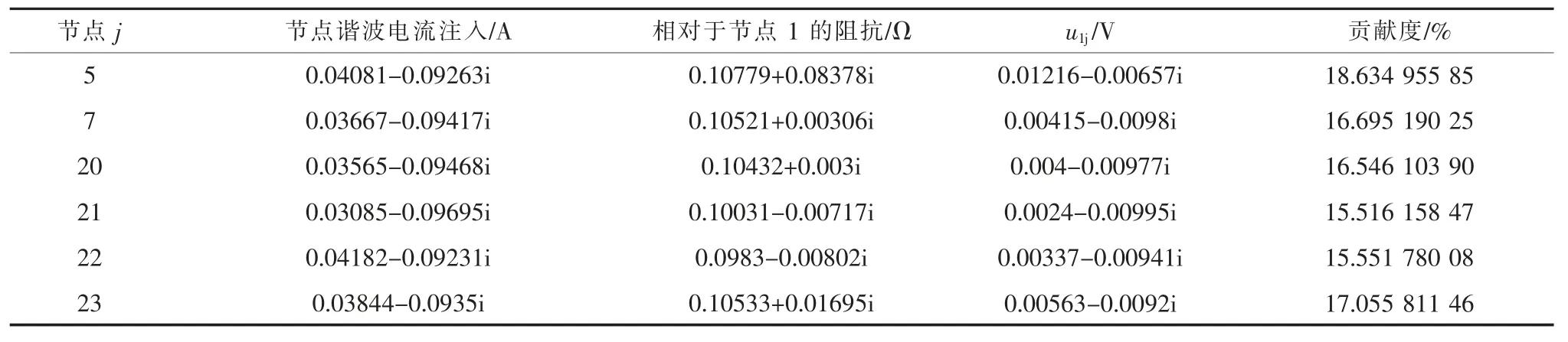
表4 节点5 谐波贡献度评估

4 结语

针对现代电网大容量、跨区域、高耦合、电力电子化的特性下，谐波责任划分所需的状态评估和计算较为困难的问题，本文将图论应用于大电网谐波数据的存储和计算，利用信赖阈求解谐波状态模型，并构建谐波贡献度作为谐波责任划分的指标，最后比对不同线路规模下图数据库和关系数据库运算速度，并在某220 kV 变电站拓扑中仿真验证所提谐波责任划分算法的正确性。