基于两侧电气量的失步保护判别新方法

张洪喜，徐晓春，谢 华,戴光武，徐海洋，卜立之

（南京南瑞继保电气有限公司，南京 211102）

0 引言

失步解列作为保证电力系统安全稳定运行的重要措施，是保障整个电网的最后一道防线[1-2]。随着大区电网互联的发展，电网的结构越来越复杂，给系统的稳定运行带来严重挑战[3]。当系统发生故障时，电网的安全会受到严重威胁[4]。目前防止因事故扩大造成全网崩溃的最基本方法是从失步断面将失步系统解列[5]。

目前国内外的失步解列方案基本上是基于联络线一侧的电气量进行判断，这种失步解列方案不能得到联络线另一侧电气量的变化特征，难以做到准确判断失步，且难以准确判断失步中心位置[6-7]。同时，当系统发生故障尤其是三相故障、转化性故障等复杂故障时，存在误判风险[8-9]。

随着光纤通信系统在现代电力系统中的广泛应用，光纤差动保护以其独特优势普遍应用于输电线路保护中[10]。光纤差动保护将对侧电流、电压等电气量传输到本侧，为开发基于两侧电气量的失步保护提供可能[11-12]。

海外多数国家或地区的电力用户对三道防线意识淡薄。往往要求将失步保护集成于线路保护装置中，通过线路保护来实现系统失步解列。因此，提供一种简单、经济和可靠的失步保护功能尤为重要。

本文提出一种基于两侧电气量的失步保护判别新方法。该方法利用线路两侧的电压量计算两侧角差和滑差，根据角差和滑差变化规律进行判别[13-14]。同时增加差动电流进行辅助判别，避免系统发生故障尤其是三相故障时误判风险[15]。该方法还考虑了系统非全相运行的情况，当系统非全相时采用健全相进行失步判别。该方法在现有差动保护装置基础上实现，不增加额外成本，不额外消耗通道资源。

1 基于两侧量的失步原理

任何复杂系统均可等值为简单两机系统，以简单两机等值系统为例进行分析。线路差动保护装置安装在线路两侧，保护装置之间通过光纤或复用设备传输电压、电流等电气量。如图1 所示。

图1 简单两机等值系统

差动保护采用基于收发路由延时一致的乒乓原理来实现同步。该方法不依赖外部对时源，能保证两侧电气量始终在同一时间断面上进行计算[16]，为基于双侧量的失步保护判别提供有利条件。

1.1 差动保护原理

差动保护基本原理是将对侧电流传输到本侧，进而计算出差动电流和制动电流，利用差动电流和制动电流的关系进行区内外故障判别。差动电流和制动电流的计算公式如下：

当系统正常运行或区外发生故障时，差动电流较小，几乎为零。当发生区内故障时，差动电流变大。差动保护动作方程如下[16]：

式中：IPkp为差动启动门槛。

当差动保护动作方程满足时，差动保护动作，将断路器跳开。

1.2 失步保护判据

差动保护将对侧电压传输到本侧，用作差动保护的辅助判据。因此，可以借助线路两侧的电压量进行失步判别。设两侧电压相量分别为Um和Un，其表达式为：

利用对称分量法，将三相电压转换为序分量，两侧正序电压表达式为：

进而计算两侧正序电压相量的相角差及滑差，分别为：

当系统发生失步时，系统两侧正序电压的相角被逐渐拉开，滑差也将变大，根据这一特征进行失步判别。

将相位角复平面上划分出几个相邻的连续角度区域，当测得的相角差连续穿越上述几个连续的角度区域且在各个角度区域范围内的停留时间满足设定的门槛时认为是一次有效的失步相位角穿越[17]如图2 所示。

图2 失步时角差变化轨迹

假设母线指向线路为正方向。当振荡中心位于保护安装处的正方向时，角差变化轨迹为：

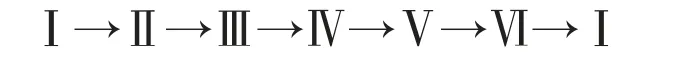
当角差变化轨迹按照上述顺序变化一周记为一次正向失步，失步次数记为Ncounter+。

当振荡中心位于保护安装处的反方向时，角差变化轨迹为：

当角差变化轨迹按照上述顺序变化一周记为一次反向失步，失步次数记为Ncounter-。

根据文献[15]，线路的衰减时间常数随着电压等级的升高而变大。当衰减时间常数较小时，两侧的角差变化较快，不会发生类似失步角差相位角穿越的现象。当衰减时间常数较大时，在线路发生三相对称故障时，过渡过程较长，可能发生类似于失步角差穿越的现象，失步保护存在误判风险。为了解决这一问题，增加差动电流判别条件。当系统正常运行，或者发生失步时，差动装置两侧的电流为穿越性电流，差动电流较小。当发生区内故障时，差动电流将变大。利用这一特征作为失步辅助判据。基于两侧量的失步保护判别逻辑如图3 所示。

图3 基于两侧量的失步判别逻辑

当系统发生失步时，失步统计次数大于设定值Nset，滑差大于设定门槛Kset，同时两侧角差小于设定值δset且差动电流小于差流启动定值时判为失步。

当区内发生故障时，差动电流将大于差动启动定值。此时失步保护逻辑中差流条件不再满足，失步保护将被闭锁。因此，该方法对系统故障具有天然的免疫力。

2 非全相运行时失步判据

2.1 非全相状态识别

在某些特殊情况下，允许系统在某一相跳开后继续运行一段时间，此时系统处于非全相运行状态[18]。非全相运行的系统更易失稳，失步保护不能退出运行。

当系统处于非全相运行时，退出运行相的电流和电压不能真实反映实际情况，会影响失步保护的逻辑判别。某相退出运行的判别逻辑如图4所示。

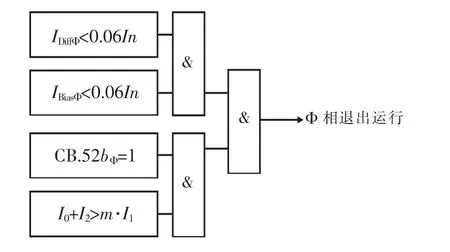
图4 某相退出运行判别逻辑

根据图4，当三相中某相的差动电流和制动电流均小于0.06In，同时该相的开关位置处于分位，且零、负序电流之和大于m 倍正序电流时，判为该相退出运行。

采用上述逻辑分对A，B 和C 三相进行判别，当且仅当其中一相退出运行时，则系统处于非全相运行状态。此时，失步保护自动采用健全相进行逻辑计算和判别。

2.2 非全相失步判别

当系统处于非全相运行时，退出运行相的电流和电压均不再参与失步保护逻辑的相关计算。包括采用健全相进行两侧正序电压计算和采用健全相进行失步用差动电流计算。

根据系统全相和非全相运行两种运行工况，形成完整的失步保护判别逻辑。失步保护判别流程如图5 所示。

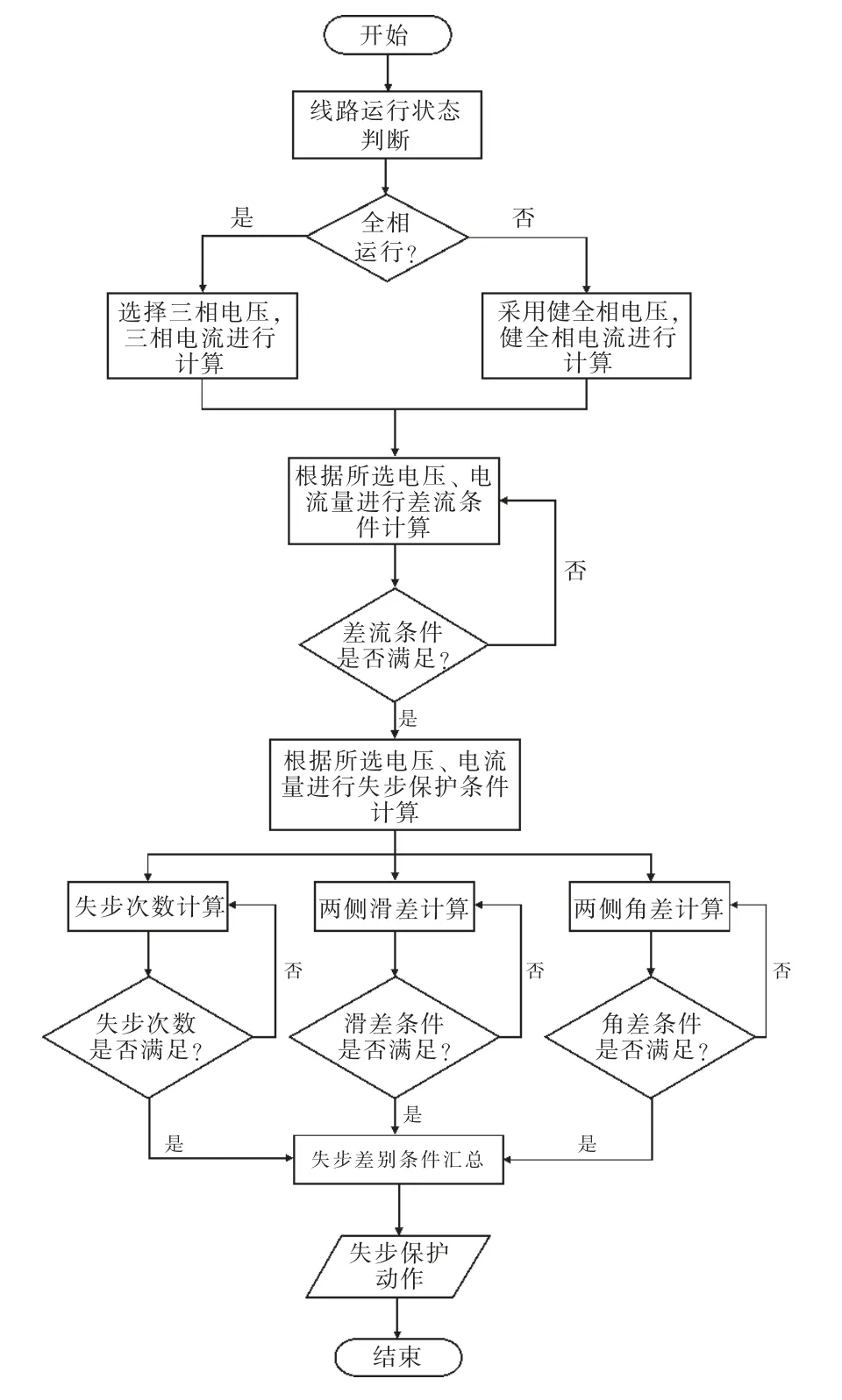
图5 失步保护判别流程

综上，根据系统失步的特征，结合差动保护功能特点，提出了基于两侧电气量的失步保护判别新方法。为了考察该方法的正确性，利用RTDS进行仿真实验。

3 RTDS 仿真测试

3.1 仿真系统介绍

为了验证本文提出的失步保护方法在实际系统中的效果，采用东南亚某国实际电网参数，搭建如图6 所示的RTDS 试验仿真模型[19-20]。

图6 RTDS 仿真模型

该系统电压等级为500 kV，系统额定频率为50 Hz，线路长度为102 km，负荷ZLoad为（1 141+j181）Ω。其他参数如表1 所示。

表1 仿真模型参数

系统两侧的电源输出频率可以通过RTDS 搭建逻辑实现自动控制。实验时，将M 侧发电机机端频率控制在50 Hz，通过改变N 侧电源输出频率，模拟系统发生失步。系统的非全相运行通过线路两侧开关进行控制。通过故障点F1 和F2 模拟区内外不同位置不同类型的故障。

差动保护安装位置如图6 所示。差动保护装置之间采用光纤直连，失步保护集成在差动保护装置中。重点考察系统全相和非全相运行状态下，系统发生失步或故障时，失步保护的动作行为。

3.2 仿真结果分析

由于篇幅限制，本文仅提供3 种典型情况下仿真结果。

失步保护功能测试。固定M 侧电源频率为50 Hz，改变N 侧电源频率，模拟系统失步状态。测试结果如表2 所示。

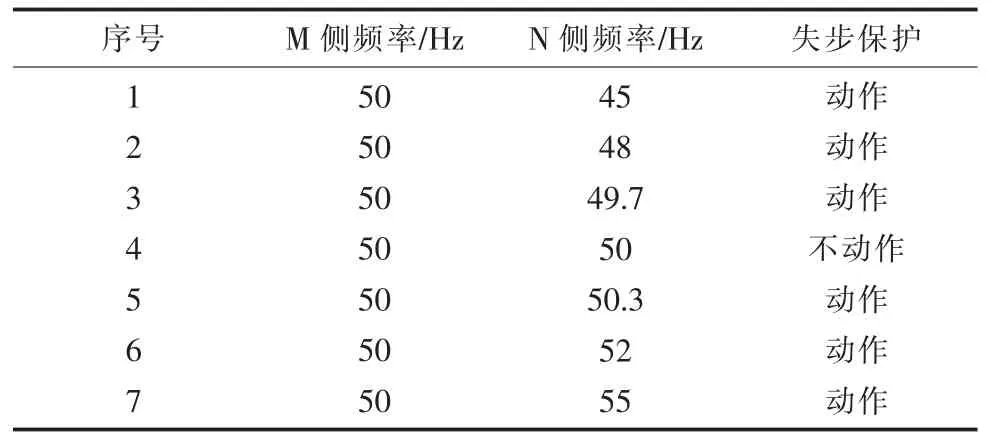
表2 系统失步时失步判别情况

由表2 可知，无论是正向失步还是反向失步，且无论失步周期的长短，失步保护均能正确动作，将系统解列。

系统发生故障时，失步保护动作行为测试。为了测试三相故障时失步保护是否会误判，将系统时间常数调整为200 ms，分别模拟区内外单相、两相和三相故障。测试结果如表3 所示。

由表3 可知，当系统发生故障，尤其是发生三相故障时，失步保护不会误判。

表3 故障状态下失步保护判别情况

系统非全相运行时，失步保护动作行为测试。分别模拟A 相、B 相和C 相三种非全相运行情况。测试结果如表4 所示。

表4 非全相运行时失步保护判别情况

由表4 可知，在系统全相运行时，失步保护不会误动。当系统非全相运行再失步时，失步保护能可靠动作。

通过以上实验，证明本文提出的失步保护方法能够正确判断系统是否发生失步；在系统发生三相故障时不误判；且在系统非全相运行时也能够正确动作。该失步保护判别方法已经应用于东南亚某国实际电网中，运行情况良好。

4 结语

本文根据电力系统失步运行的特征，并结合线路差动保护的特点，提出了一种基于两侧电气量的失步保护判别新方法。该判别方法利用线路两侧的电压量计算两侧角差和滑差，根据角差和滑差变化规律进行判别。同时增加了差动电流作为辅助判据，避免系统发生故障尤其是三相故障时误判风险。该方法还考虑了系统非全相运行的情况，当系统非全相时采用健全相进行失步判别。该方法在现有差动保护装置的基础上实现，不增加额外成本，不额外消耗通道资源，便于工程应用。该方法不受系统运行方式影响，定值整定简单。通过RTDS 仿真实验，验证了该方法的正确性。