数学问题解答
2021年5月号问题解答
(解答由问题提供人给出)
2601(1)题目在第5期刊出后,供题人安振平老师又复核了问题,发现题目中的条件a+b+c=abc是多余的,故在解答中去除.在此我们对安老师的认真细致表示感谢!已知a,b,c∈R,求证:
(a2+1)(b2+1)(c2+1)≥(ab+bc+ca-1)2.
(陕西省咸阳师范学院教育科学学院 安振平 712000)
证明已构造复数z1=1+ai,z2=1+bi,z3=1+ci,则
(a2+1)(b2+1)(c2+1)=(|z1||z2||z3|)2
=|z1z2z3|2
=|(1+ai)(1+bi)(1+ci)|2
=|[(1-ab)+(a+b)i](1+ci)|2
=|(1-ab-bc-ca)+(a+b+c-abc)i|2
=(1-ab-bc-ca)2+(a+b+c-abc)2
≥(ab+bc+ca-1)2,
所以(a2+1)(b2+1)(c2+1)≥(ab+bc+ca-1)2.
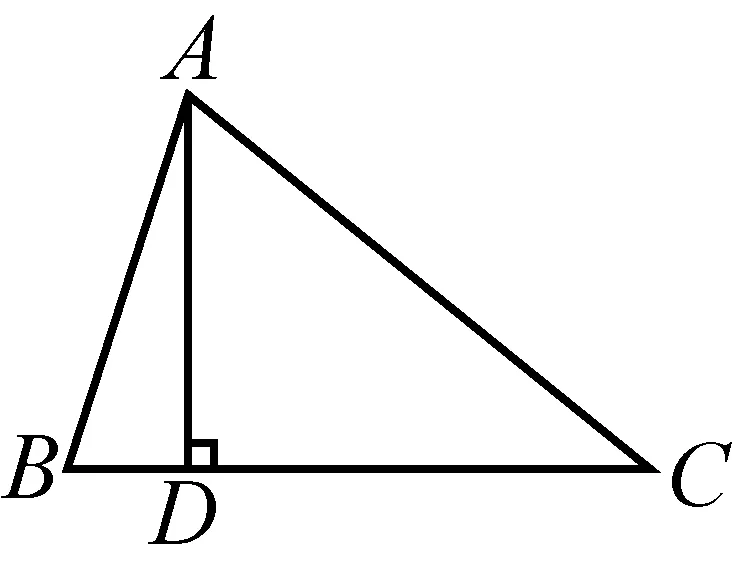
2602已知,在△ABC中, ∠ACB=90°,CD⊥AB于点D,点F1,F2在BC上,且∠CAF1=∠BAF2,AF1,AF2与CD分别交于点E1,E2.
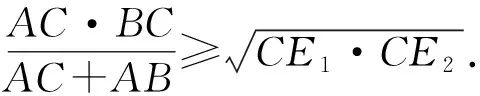
(北京市朝阳区教育研究中心 蒋晓东 100028;北京市朝阳区芳草地国际学校富力分校 郭文征 100121)
证明如图,因为∠ACB=90°,
所以∠CAF1+∠AF1C=90°.
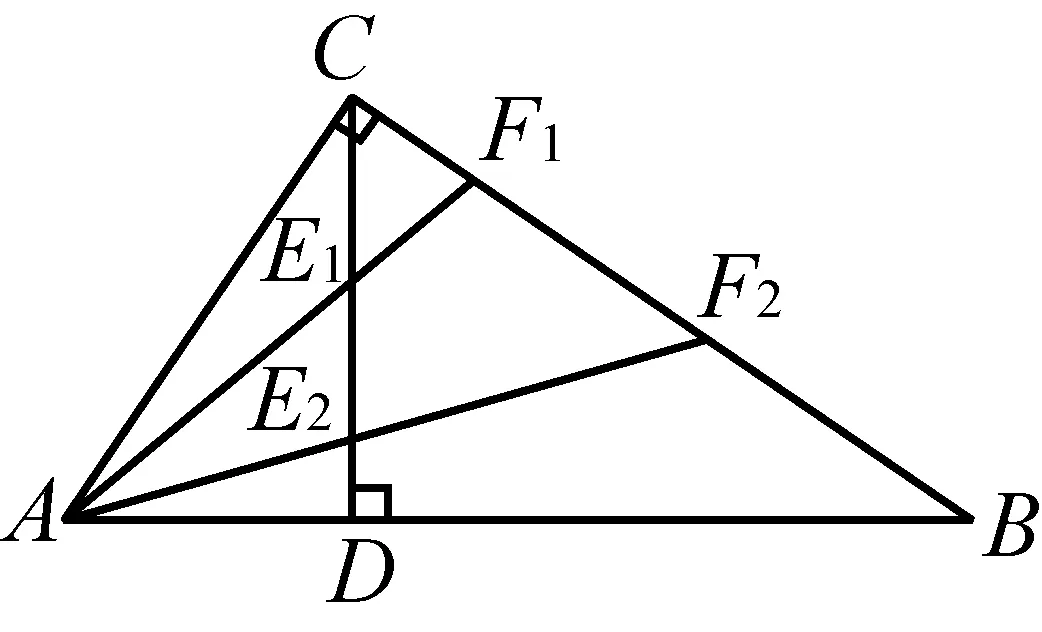
因为CD⊥AB,
所以∠BAF2+∠AE2D=90°.
因为∠CAF1=∠BAF2,
所以∠AE2D=∠AF1C.
又∠AE2D=∠E1E2F2,
所以∠AF1C=∠E1E2F2.
从而E1,E2,F2,F1四点共圆.
所以CE1·CE2=CF1·CF2.
因为∠CAF1=∠BAF2,
所以AF1,AF2为△ABC的∠CAB的内等角线.
由三角形的内等角线定理,得
⟹AC2[BC2-BC(CF1+CF2)+CF1·CF2]
=AB2·(CF1·CF2)
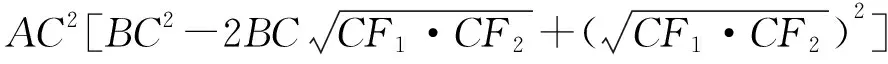
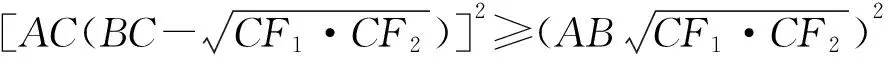
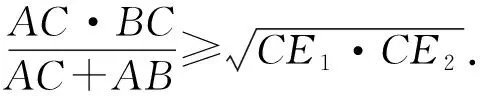
当且仅当∠CAB的内等角线合并为∠CAB的平分线时,不等式中的等号成立.
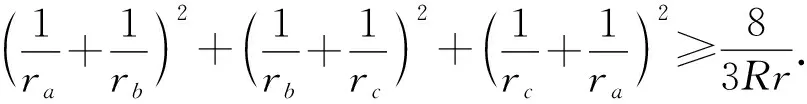
(天津水运高级技工学校 黄兆麟 300456)
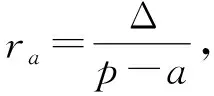
那么就有
又由熟知的欧拉比公式
我们可得
(1)
利用三元均值定理及两个熟知的三角公式
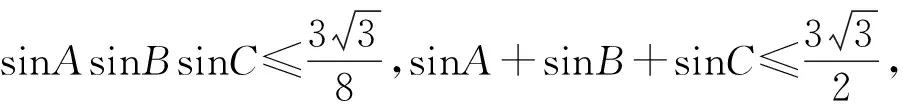
即不等式(1)成立,故原不等式成立.
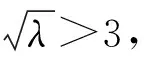
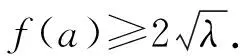
2604已知a,b,c>0,且abc=1.
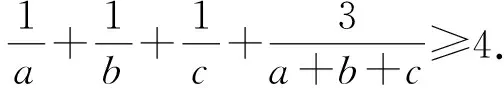
(湖北省公安县第一中学 杨先义 434300)
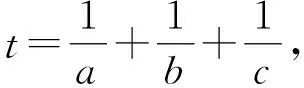
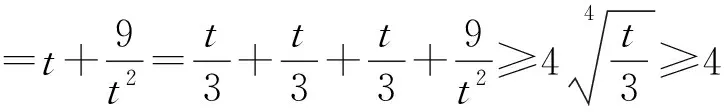
(2)由于abc=1,所以a,b,c必有不大于1者,不妨设0 则f(a)是减函数, 当且仅当a=1取等号,此时bc=1, 综上所述,使不等式 (安徽省六安第二中学 陶兴红 237005 ) 解过A作AD⊥BC,垂足为D, 由tanB=4tanC,可得 可设BD=x,CD=4x,AD=h, 则由勾股定理得 b2=16x2+h2,c2=x2+h2, 所以由均值不等式得 2021年6月号问题 (来稿请注明出处——编者) 2606设凸四边形ABCD的边长和对角线长分别为BC=a,CD=b,DA=c,AB=d,AC=m,BD=n,四边形的面积为Δ,则 (a+c)2+(c+d)2-m2-n2≥4Δ, 当且仅当四边形为正方形时等号成立. (山东省泰安市宁阳第一中学 刘才华 271400) 2607设数列{an}的通项公式为 (河南质量工程职业学院 李永利 467001) 2608已知a,b,c∈R,且a,b,c中至多一个为0,则有 ≥ab+bc+ca. (云南省大理州漾濞县第一中学 秦庆雄 范花妹 672500) (浙江台州市洪家中学 邬天泉 318015) 2610设任意△ABC的三边长,对应的三中线分别为a、b、c,mambmc,则有 当且仅当△ABC为正三角形时等号成立.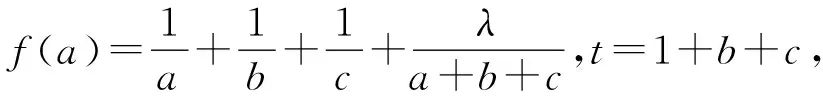
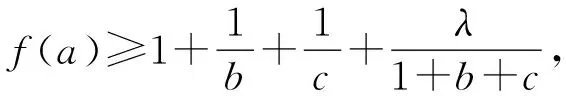
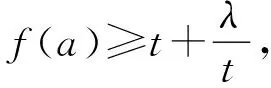
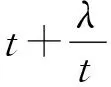
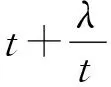

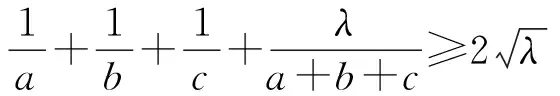
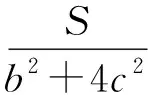
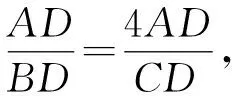
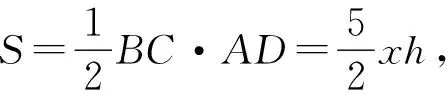
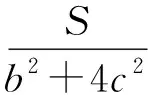
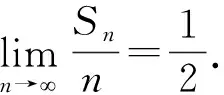
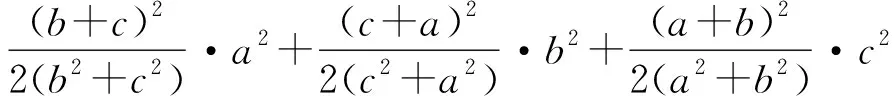
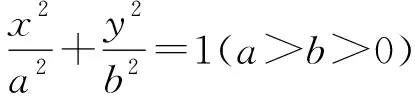
——长春市朝阳区明德小学简介

