基于改进AHP 的无人机作战能力量化研究

王 彪，赵建新，陈 兵，高腾飞，张宏映

（北方自动控制技术研究所，太原 030006）

0 引言

在近期的纳卡冲突中无人机首次较大规模的作战应用引发了世界范围内的高度关注，阿塞拜疆利用TB-2 型中空长航时武装无人机、远程遥控精确制导巡飞弹、Hermes 长航时侦察无人机、MAM-C激光制导炸弹等大量不同种类的空中无人装备，使纳卡国防军前线的导弹阵地、炮兵阵地、弹药仓库等重要军事目标遭到沉重打击。

可以看出，在实战背景下投入应用的无人机平台及载荷类型较多，兵力资源构成较复杂，而迅速完成敌我双方兵力对比分析，是开展后续作战部署的重要准备工作，因此，本文针对无人机及载荷性能指标设计一种作战能力量化方法，可以辅助指挥官快速进行敌我双方兵力对比概算、兵力资源分析等，对无人武器系统论证、无人机作战模拟等论证分析工作也有较大的实际应用价值。

在武器装备能力量化评估方面，自上世纪50年代开始，研究学者们便做了大量工作，张彦芳［1］利用AHP 对陆军典型武器装备作战能力进行量化计算，但其标度方法引入了较大主观性误差；徐瑞恩［2］给出定性定量计算武器作战能力的指数方法，但其作战能力层次结构理论不够完善；郑建华［3］构建了海军武器装备作战能力层次图，但没有给出具体能力指标的量化评估方法；杨晓［4］基于AHP 提出三标度法、矩阵拟优等改进方法，提高了计算效率。

上述几种基于AHP 的量化评估方法，对无人机装备作战能力量化均有直接或间接指导意义，但还存在某些问题，如描述作战能力的层次化结构不完善，无法充分描述无人机装备复杂作战能力构成；同级别不同量纲作战能力的重要程度对比标度方法不完善等。本文针对上述不足，对传统AHP 作出改进，以期较好解决上述问题，实现无人机装备作战能力量化。

1 AHP 基本原理及其改进

层次分析法是由美国学者T.L.Saaty 于上世纪70 年代提出的一种偏向实际应用的决策方法［5］，可以将一个对象以清晰有序的层次化结构表示，按照一定的标度方法，对层次化结构中元素进行两两对比，通过数学表达及处理实现定性、定量分析。

本文主要针对传统AHP 的两点不足作出改进：

第1，传统AHP 仅设置单一目标层，数据较单薄，无法充分描述现代化作战环境中的无人机装备特性。本文通过构建无人机装备作战能力量化的多层次结构图，从准则、指标等多个角度充分描述多种不同用途的无人机装备作战能力指标。

第2，传统AHP 采用1-9 标度法确定层次化结构元素的相对重要程度，虽然降低了对操作人员的专业知识要求，但其线性标度方法并不能客观反映方案权重，引入了较大的人为主观误差，产生的非一致性可能破坏AHP 的指标量化排序功能，影响能力量化准确性。本文通过建立重要程度标度的指数关系，以期降低指挥人员的主观经验对求解过程的影响误差，提高判断矩阵一致性。

2 基于改进AHP 的作战能力量化步骤

通过构建无人机装备作战能力层次结构，对各种不同指标进行充分描述，采用指数标度方法进行权重计算并进行一致性检验，具体步骤如下：

2.1 构建装备作战能力量化层次

根据实战应用条件下无人装备性能对作战活动实施的影响因素，构建4 层作战能力指标量化体系：目标层-准则层-指标层-实例层［7］。其中，目标层即对无人机装备作战能力进行量化评价；准则层即根据装备作战应用确定若干量化准则；指标层即装备具体作战性能指标；实例层即待进行作战能力量化的各对象。装备作战能力量化层次结构如图1 所示。

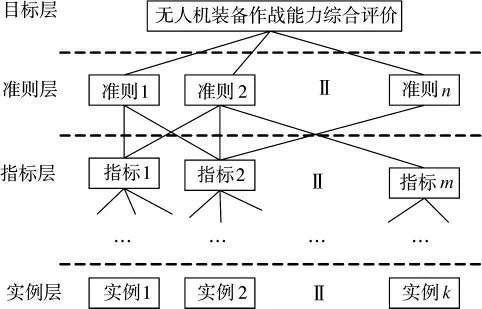
图1 装备作战能力量化层次结构

2.2 构造同层元素重要度正互反矩阵

无人机装备作战能力层次结构表明了各层内部元素、层与层之间元素的隶属关系，AHP 将元素赋值问题转化为元素之间重要程度对比问题。根据调查分析，一般对两要素进行重要度对比时，两个“稍微重要”的复合等同“明显重要”［6］，两个“明显重要”的复合等同“非常重要”，两个“非常重要”的复合等同“极度重要”，其重要程度对比可以用指数关系描述：

表1 中5 个对比级别数值之间构成比例关系，能较好反应各定性的相互关系。

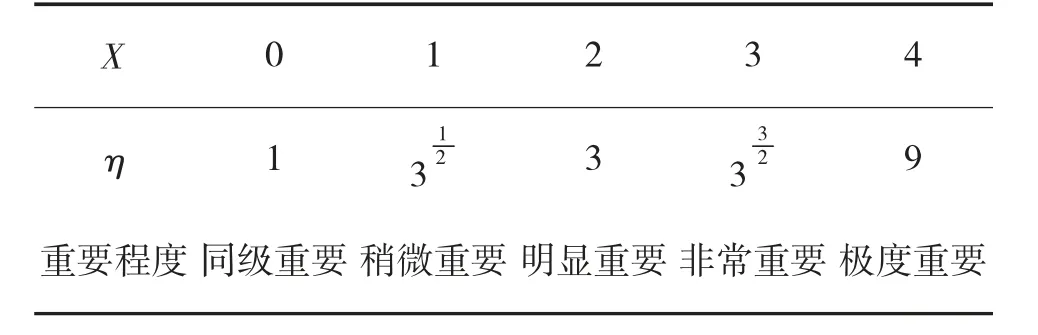
表1 重要程度对比值

由多位无人机作战相关专家分析对比各层内元素的重要程度，根据指数标度法，构建正互反矩阵C。

矩阵cij中表示层内元素xi与元素xj的对比关系，具体如下所示。

反之则用相应标度值的倒数表示。

2.3 权重计算

2.3.1 层内元素权重计算

通过相关数学知识易验证，上述正互反矩阵C具有唯一且非零的最大特征值为λmax。

设层内元素权重向量为W=（ω1，ω2，…，ωn）T，通过矩阵计算可以验证：

即矩阵C 的最大特征值所对应的特征向量W为各个元素的权重值。

2.3.2 层次权重矩阵计算

2.3.3 组合权重计算

构建层次权重矩阵L（i）后，按层次递增顺序，递阶计算各实例组合权重。

第k 层元素为层次结构模型中各层次权重矩阵的乘积，即各实例的组合权重向量，记作Z（k）。

2.4 矩阵一致性检验

矩阵一致性检验C.R. 由计算一致性指标和随机一致性指标确定。

其中，C.I.由矩阵阶数及λmax确定，表2 为1-15 阶据矩阵计算1 000 次的随机一致性指标，作为R.I.参考依据。

表2 1-15 阶矩阵一致性指标

最终，根据式（7）进行矩阵一致性检验，验证本文方法的正确性和可行度。

当C.R.＜0.1 时，认为正互反矩阵具有较好的一致性，较好反应了事物相应特征关系。

2.5 指标的标准化处理

对无人机进行作战能力量化评估时，涉及到多层不同种类、不同含义的能力指标，为直观体现不同种类无人机作战能力水平，采用向量归一化方法对无人机作战能力指标进行标准化。

3 无人机装备作战能力量化指标体系

无人机作为一种基于地面站引导的空中自主飞行作战装备，其作战能力受地面人员操作素质、气候环境、作战对象等多方面影响，但本文所分析问题仅针对无人机及相关装备的静态作战能力指标，即排除外界影响因素，针对标准操作环境中无人机装备所能发挥的各基本能力指标，实现作战能力体系量化。

无人机遂行作战任务时，除飞行器本身作战性能外，还可附加挂载武器载荷、侦察载荷、电子设备、救援物资等，实现不同作战用途。因此，本文将无人机基本能力大致概括为飞行机动能力、通信能力；将无人机附加能力概括为火力打击能力、侦察能力、抗侦察能力、电子对抗能力和作战保障能力，根据无人机挂配载荷不同，利用不同组合进行作战能力量化计算［9］。

表3 无人机装备作战能力量化指标体系

4 改进AHP 实现作战能力量化实例

以某A、B、C、D 4 种型号察打一体无人机为例，将飞行机动能力、通信能力、火力打击能力和侦察能力进行统一组合，代表各型察打一体无人机作战能力，基于本文设计的作战能力量化方法，针对准则层的4 种能力进行量化计算［10］。

4.1 构建察打一体无人机作战能力层次结构

如图2 所示。

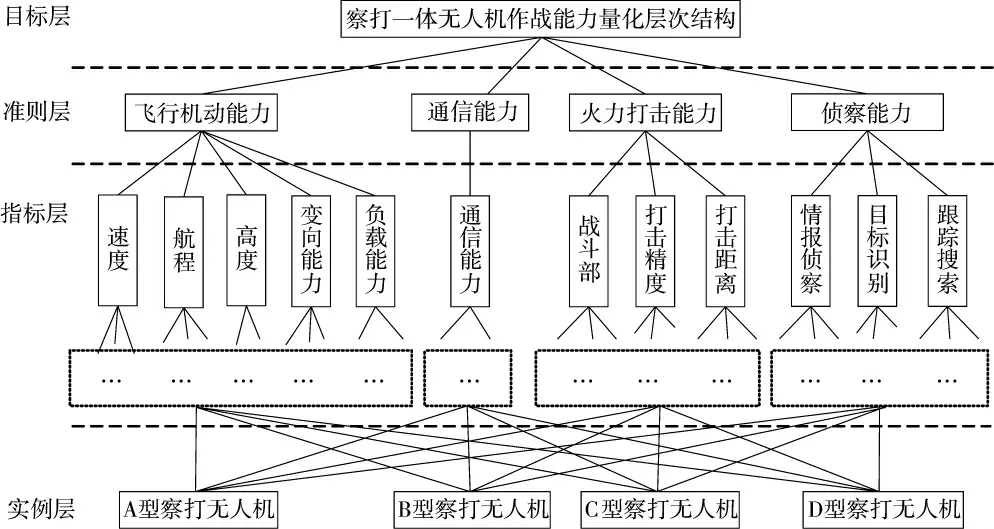
图2 某四型察打一体无人机作战能力量化层次结构示意图

4.2 权重计算及一致性检验

根据无人机相关专家对准则层进行相对重要程度标定，得到目标层-准则层、准则层-实例层的重要程度标度如表4～表8 所示。

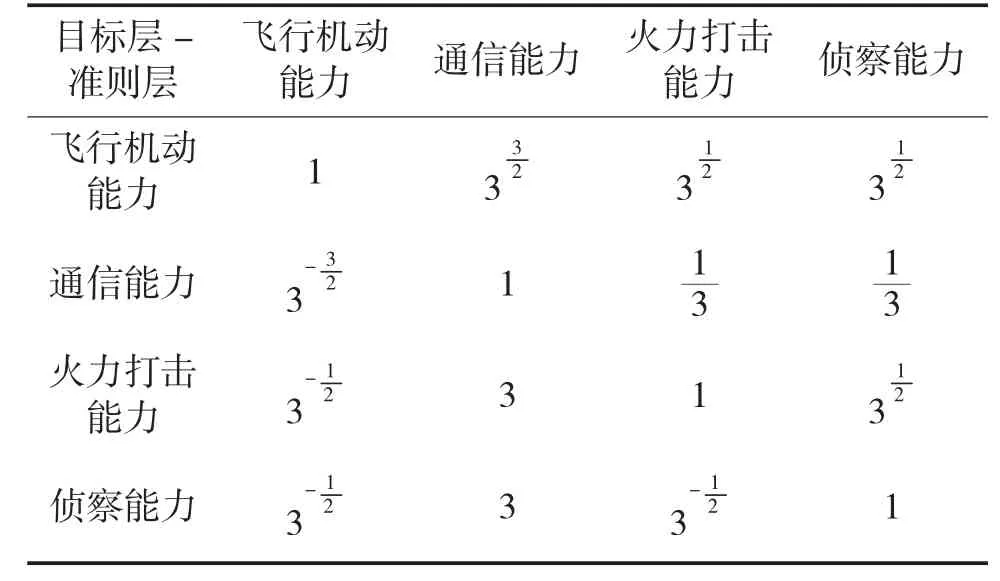
表4 目标层-准则层重要程度对比标度

根据表4 计算得到最大特征值λmax=4.139 1，显然，该矩阵满足一致性检验，λmax对应的特征向量W=［0.686 8，0.132 2，0.630 6，0.336 4］T，代表准则层4 个层内元素的相应权重。

根据表5 计算得到λmax1=4.154 5。W1=［0.476 0，0.824 6，0.218 2，0.214 2］T为λmax对应的特征向量，代表飞行机动能力准则下的各实例层元素的相应权重。

表5 飞行机动能力-实例层对比标度

根据表6 计算得到λmax2=3.999 9，W2=［0.462 9，0.801 8，0.267 2，0.267 2］T为λmax对应的特征向量，代表通信能力准则下的各实例层元素的相应权重。

表6 通信能力-实例层对比标度

根据表7 计算得到λmax3=4.037 9，W3=［0.804 7，0.528 8，0.176 3，0.204 3］T为λmax对应的特征向量，代表火力打击能力准则下的各实例层元素的相应权重。

表7 火力打击能力-实例层对比标度

根据表8 计算得到λmax4=4.154 5，W4=［0.298 3，0.894 9，0.236 8，0.232 5］T为λmax对应的特征向量，代表侦察能力准则下的各实例层元素的相应权重。

表8 侦察能力-实例层对比标度

由以上计算得到目标层- 准则层的权重矩阵L（1），准则层-实力层的权重矩阵L（2）。

由式（4）可计算得到实例层组合权重向量Z（3）。

综上可得4 型无人机的作战能力量化计算结果，对组合权重向量Z（3）进行归一化处理，计算结果如下页表9 所示。

能力量化 飞行机动能力 通信能力 火力打击能力A 型无人机 0.476 0 0.462 9 0.804 7 B 型无人机 0.824 6 0.801 8 0.528 8 C 型无人机 0.218 2 0.267 2 0.176 3 D 型无人机 0.214 2 0.267 2 0.204 3侦察能力0.298 3 0.894 9 0.236 8 0.232 5综合作战能力0.324 6 0.425 9 0.122 6 0.126 9 C.R.检验0.057 87 0.0000 374 5 0.0141 9 0.0578 7

可以看出，B 型无人机飞行机动能力最强，A 型无人机次之，C、D 两型无人机飞行机动能力接近；B型无人机通信能力最强，A 型无人机次之，C、D 两型无人机通信能力接近；A 型无人机打击能力最强，B型无人机次之，C、D 两型无人机打击能力接近且均较低；B 型无人机侦察能力最强，A、C、D 三型无人机侦察能力接近且均较低。综合量化无人机飞行机动能力、通信能力、火力打击能力、侦察能力后，可以得出，B 型察打一体无人机作战能力最强，A 型无人机次之，C、D 无人机作战能力一般且两者接近［11］。

通过基于传统AHP 的一致性检验，C.R.均远小于0.1，证明本文计算方法较好地实现了对4 型察打一体无人机作战能力量化评估，具有较好的实际应用价值。

5 结论

无人机装备作战能力量化对战前兵力分析、作战模拟演练等具有较大的研究意义，本文基于传统层次分析法的几种不足进行了完善和改进，用较充分、合理的层次化结构描述了无人机装备能力，实现了无人机作战能力的量化对比评估，并通过检验验证了本方法对多种类型无人机装备作战能力量化的可行性和实用性，为兵力资源分析、战术战法决策等作战活动提供了合理的数据支撑，具有较高的军事应用价值。