基于自适应遗传算法改进的BP神经网络卡钻事故预测
刘海龙,李 彤,张奇志
(1.西安石油大学 电子工程学院,陕西 西安 710065;2.西安石油大学 陕西省油气井测控技术重点实验室,陕西 西安 710065)
0 引言
钻井过程中,由于各种原因造成的钻具陷在井内不能自由活动的现象,称为卡钻,在处理卡钻事故时,时间长、成本高、效率低,且极易引发井塌、井漏、井喷等连锁事故,严重的或导致井眼报废,甚至需要填井侧钻[1],给石油企业带来巨大经济损失,威胁现场作业人员的生命安全。因此,在石油钻井过程中,及时预测卡钻事故的发生具有重要意义[2]。
传统卡钻事故仅能通过相应仪器仪表中的数据变化得知是否发生,基本处于黑箱状态,且用传统的线性数学模型无法表达这一复杂过程。随着智能控制技术的发展,相继提出了多种控制手段和方法来预测卡钻事故的发生,主要有通过建立时序ARMA 模型结合神经网络的卡钻预测[3];基于专家系统构建的本体和CBR 钻井工程风险决策模型[4];基于风险概率和模糊理论的井下事故风险程度判别模型预测[5⁃6];通过事故树分析法分析井下事故,根据专家系统实现判别和预测[7];Murillo 基于自适应模糊逻辑建模构建的卡钻预测模型;斯伦贝谢石油公司通过建立风险识别信息系统,对钻井全过程风险进行了识别评价[8];文献[9]考虑了钻井液性质、钻井过程中形成的泥饼特征等使用主动学习方法(ALM)建立了预测模型;文献[10]根据LWD 建立实时的随钻测量卡钻预测系统[10]。以上研究均从不同角度和方法对卡钻预测进行了一定探索,但效果均不能完全满足施工现场的需求。
由于BP 神经网络的非线性映射能力,因此将其应用于卡钻事故预测是主要研究趋势之一。本文在前期研究基础上,设计了一种BP 神经网络卡钻预测模型,针对BP 神经网络模型易陷入局部极小值使模型失效的问题,采用自适应遗传算法对BP神经网络权值和阈值进行优化,建立了AGA⁃BP 神经网络卡钻预测模型。经实验结果对比,自适应遗传算法优化的BP神经网络较未优化前BP 神经网络模型具有更高的稳定性和精度,证实了AGA⁃BP神经网络在卡钻预测方面的积极作用。
1 自适应遗传算法改进的BP 神经网络在卡钻预测中的应用
1.1 BP 神经网络卡钻预测模型设计
BP 神经网络的核心思想是误差的反向传播,通过期望输出与实际输出之差反向传回网络各层,对误差逐层的连接权值进行修正。在学习中,通过设置迭代次数和停止条件来结束整个学习训练过程。
BP 神经网络卡钻预测模型的建立具体如下:
1)输入层设计。通过查阅西北某地区十余口井相关的钻井历史数据,总结井下复杂事故发生和处置过程,从钻井液性能、钻井参数、工程参数三种要素中筛选出钻井井深、密度、漏斗粘度、含砂、滤矢量、转速、排量、泵压、机械钻速9 个变量作为神经网络的输入变量。
2)输出层设计。对于确定的样本数,网络输入太少不足以表达样本中蕴涵的全部规律,太多则由于样本信息少而得不到充分的训练。本文中输出层节点数为1,采用二分类的思想,当预测卡钻发生时,输出为1,钻井过程正常钻进时,输出为0。
3)隐含层设计。隐含层对网络性能有很大影响,是导致“过拟合”现象的直接原因[11]。在实际构建中,一般通过经验公式运用“试凑法”确定具体节点数。本文使用的经验公式如式(1)所示。

式中:S表示隐含层节点数;m和n分别代表输出层节点数和输入层节点数;a为常数,一般取值为1~10。根据上文可知,m=1,n=9,代入式(1)得S=5~14。经测试,确定当隐含层节点数S=10 时,模型效果最理想。
4)网络参数设计。BP 神经网络经典训练方法常采用梯度下降法,即Traingd 训练函数,然而前期研究结果表明,运用梯度下降法的网络收敛速度较慢,易陷入局部极小,且在学习过程中易发生振荡,影响整个网络的性能。Levenberg⁃Marquardt 优化算法属于“爬山”法的一种,其对于过参数化问题不敏感,能够有效处理冗余参数问题,使代价函数不易陷入局部极小值,因此选用Trainlm 作为本模型的训练函数。
1.2 自适应遗传算法优化过程
BP 神经网络以梯度下降法为核心思想,无法避免使模型有机率陷入局部极小,导致BP 神经网络卡钻预测模型的失效。
遗传算法是一种全局搜索的仿生学优化算法,它模拟自然界生物遗传变异的机制,遵循优胜劣汰规则。在BP 神经网络中,网络初始权值的选择对卡钻事故预测的结果有较大影响,随着迭代对权值的修正,使整个网络趋近理想的非线性映射结果。通过遗传算法对BP 神经网络的权值和阈值寻找全局最优解[12],两者相结合,可以构建具有学习、记忆和非线性映射能力的全局搜索神经网络,从而提高整个模型的收敛速度和精确性。因此,本文建立自适应遗传BP 神经网络卡钻预测模型的具体流程如图1 所示。

图1 预测流程图
自适应遗传算法优化过程主要包括下列步骤:
Step1:种群的编码和初始化。种群由个体组成,这些个体代表了解集中的每个独立解,采用实数型编码方式可以更好地接近问题空间,扩大搜索范围,避免了局部极小值。
设输入层到隐含层间连接点权值总个数为W1,阈值个数为B1,隐含层到输出层间权值个数为W2,阈值个数为B2,编码长度R为:
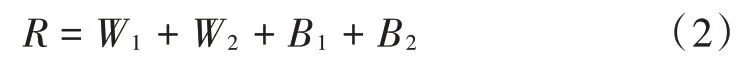
由1.1 节设置BP 网络结构可知:R=90+10+10 +1=111。
Step2:适应度函数设计。通过设置合理的适应度函数,可使包含BP 神经网络权值、阈值信息的种群通过每一代的遗传操作,逐渐进化出适应度高的染色体编码,从而完成最优寻解工作[13]。卡钻预测网络选择输出与期望之间均方误差的倒数作为遗传算法适应度函数。
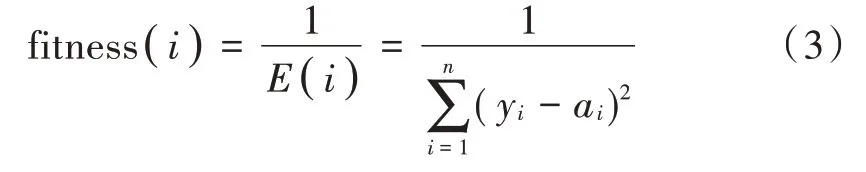
式中:yi为输出层各神经元输出值;ai为期望值。
Step3:选择、交叉、变异操作。遗传算法的选择操作决定可以作为父辈进入到下一次遗传变异过程中的个体。依据筛取适应度高的个体进入下一代的策略思想,主要分为依靠适应度大小决定被选择概率大小的轮盘赌法、循环多轮选优的锦标赛法、按适应度大小排序选择法等[14]。本文使用适应度排序法。
算法中运用交叉和变异保持种群的活性。传统的遗传算法中交叉和变异概率固定,易造成在寻优过程中前期多样性差、搜索能力弱、后期优良个体难以保留的问题。本文通过设置自适应交叉和变异概率来改变此情况。

式中:Pc和Pm分别为交叉概率和变异概率;Pc1和Pm1分别为初始交叉概率和变异概率,取0.5 和0.05;favg为当前整个种群的平均适应度值;fmax为当前种群中的最大适应度值;f′为当代交叉个体中较大的适应度值;f为当代变异个体的适应度值。
2 AGA⁃BP 神经网络卡钻预测的实现
考虑到大部分钻井过程中的实际施工情况,训练样本的选取范围包含有压差卡钻、泥包卡钻、缩径卡钻、砂桥卡钻等状态。同时论文中所选的100 组训练样本和40 组测试样本数据均来自西北某地区十余口井的钻井历史记录,训练样本和测试样本分属不同的井口。为保证网络的可靠性,保持井口的地质条件一致,井口所在区域均属鄂尔多斯盆地伊陕斜坡地貌,井下多为泥砂岩混合土质。部分样本数据如表1 所示。

表1 部分训练样本数据
将100 组训练样本和40 组测试样本通过BP 神经网络进行训练和测试得到的结果如图2 所示。
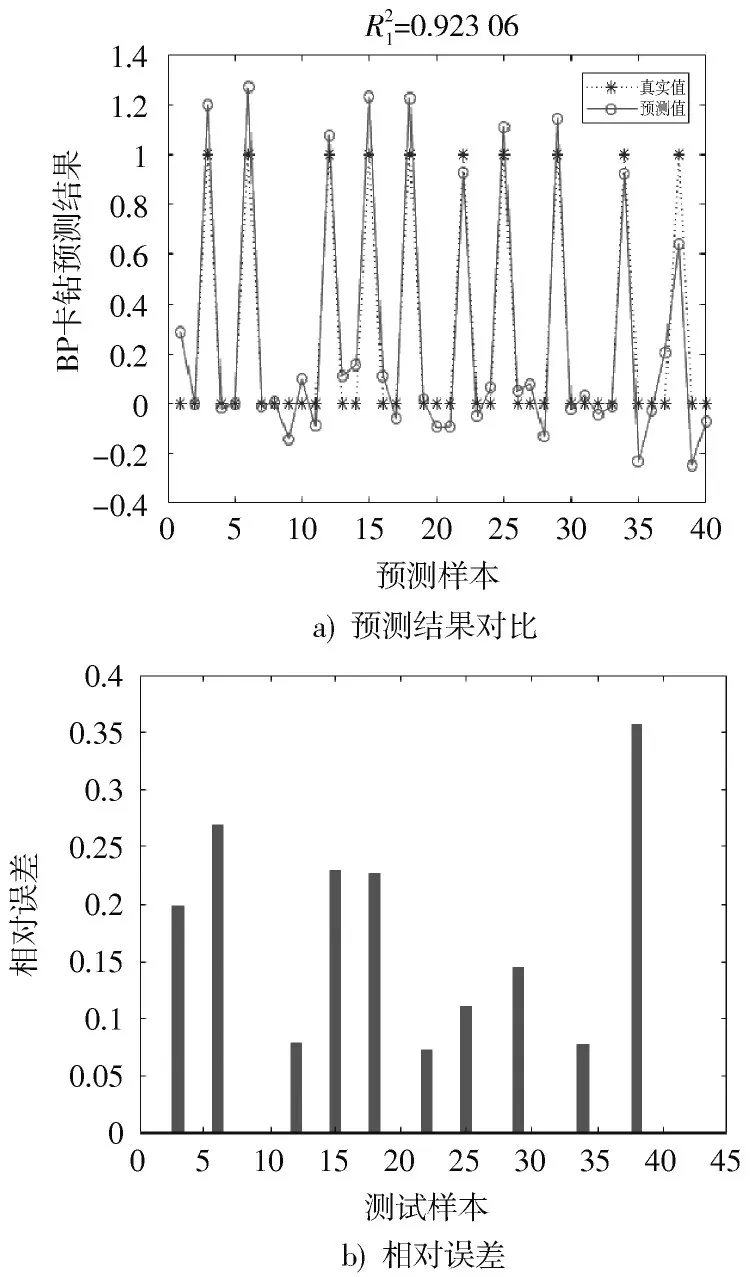
图2 BP 神经网络卡钻预测结果及误差
观察图2a),判断为卡钻的10 组样本中,模型预测输出的幅值位于(0.7,1.3)之间,剩下30 组正常样本的预测值在(-0.2,0.3)之间。
由图2b)可以看到,虽然测试样本的相对误差最大值小于0.37,但模型整体预测效果仍有很大改进空间以提高鲁棒性。
使用决定系数R2评价神经网络可靠程度,R2∈[0,1]。
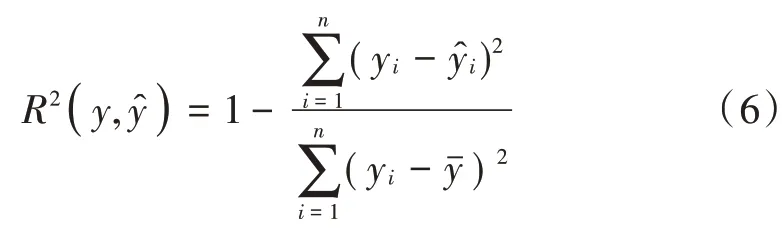
式中:y为预测值为期望值为平均值;n为样本数。
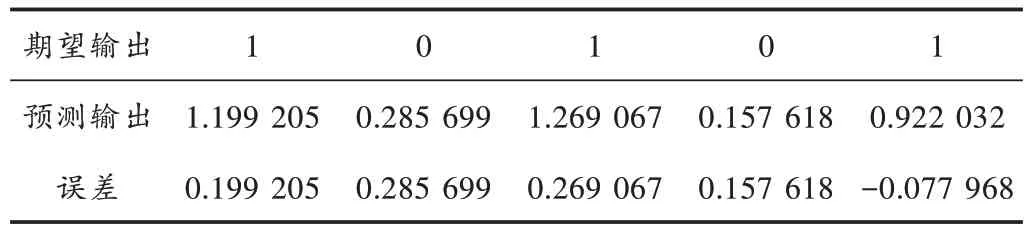
表2 BP 预测结果误差
预测结果的均方误差(MSE)值为0.019 622,计算公式为:

遗传算法通过选择适应度高的个体进入下一代,设定好BP 神经网络的网络结构后,对权值和阈值进行编码,通过自适应遗传算法进行寻优运算,其适应度随遗传代数变化曲线如图3 所示。
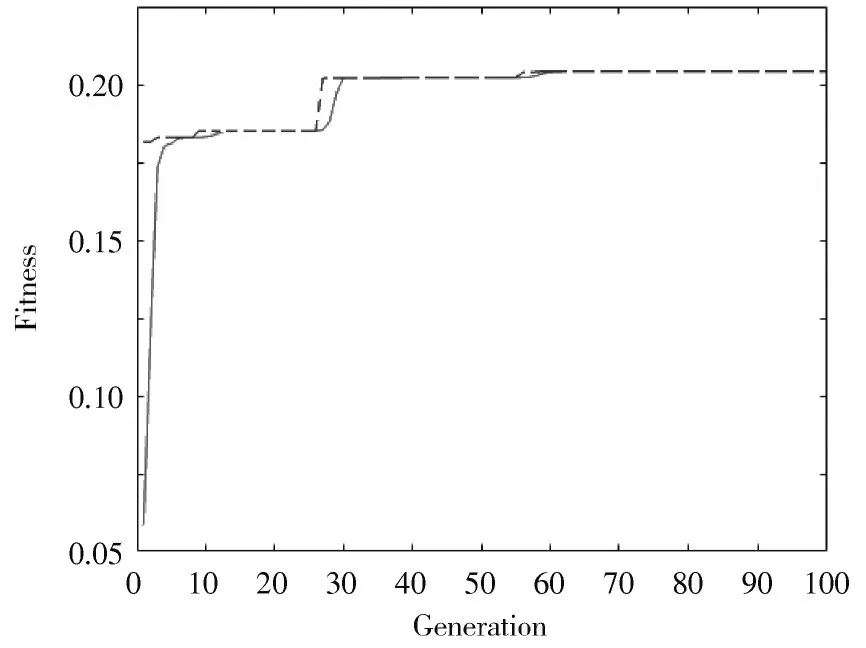
图3 遗传寻优过程
图3 中,虚线代表种群平均适应度,实线代表每代种群的最佳适应度,当迭代次数达到62 次时,最佳适应度值为0.205 1,此时为最佳适应度值,该适应度对应的权值和阈值为最佳值。
为检验网络的性能和泛化能力,将40 组测试数据输入训练好的网络中,训练结果如图4 所示。
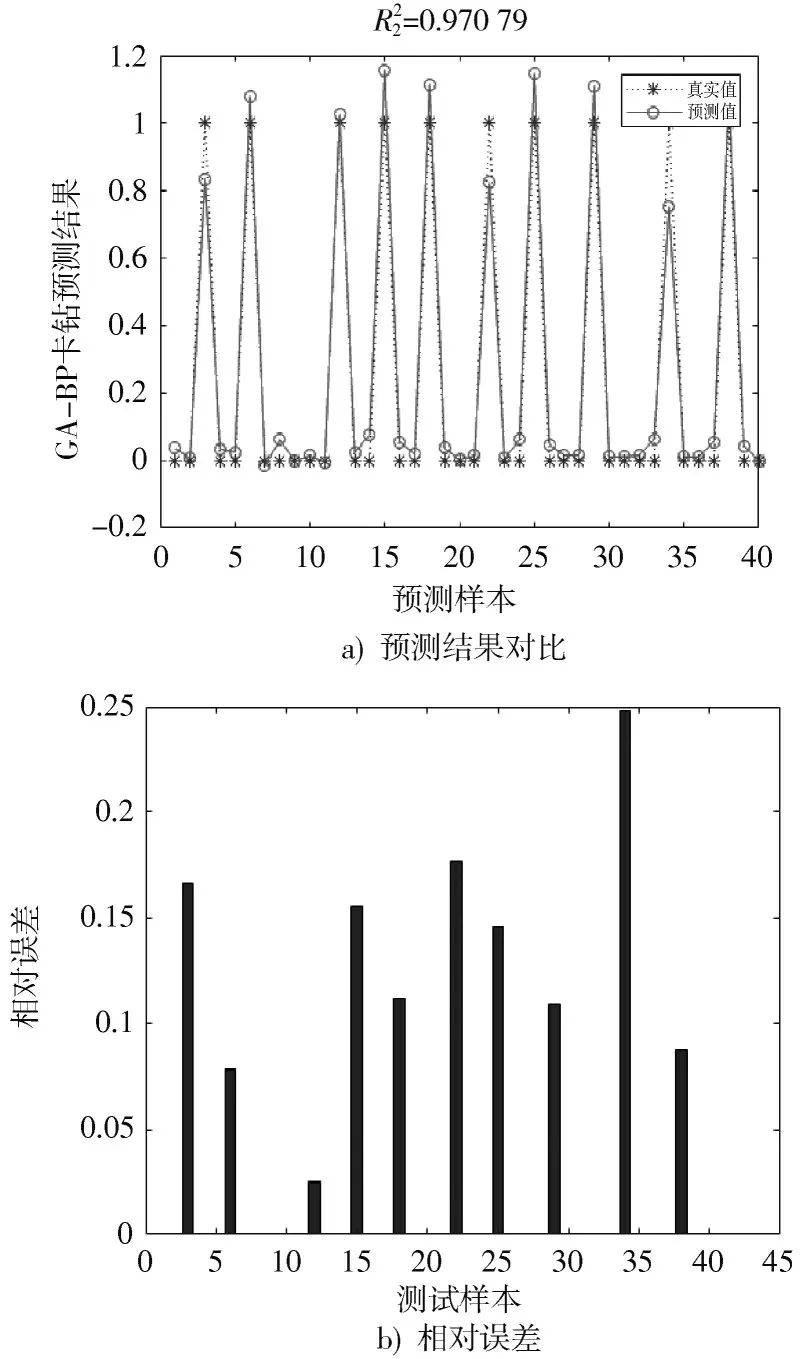
图4 AGA⁃BP 神经网络卡钻预测结果图
分析图4 可知,自适应遗传算法优化过的BP 神经网络卡钻预测模型决定系数=0.970 79,大于与未优化前相比更接近于1,拟合结果更佳。
模型预测输出的幅值位于(0.8,1.2)之间,剩下30 组正常样本的预测值在(-0.05,0.1)之间,部分测试样本期望输出与网络输出误差如表3 所示。
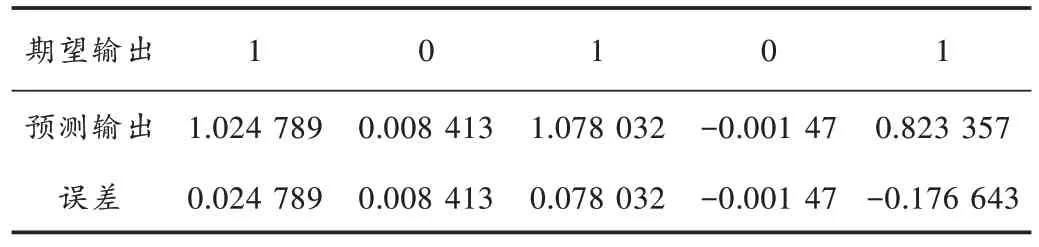
表3 AGA⁃BP 预测结果及误差
经式(7)计算,预测结果的MSE 值等于0.006 033,相比于BP 神经网络模型预测结果均方误差减小了0.013 589,准确度提高了约30.75%。网络性能比较如表4 所示。
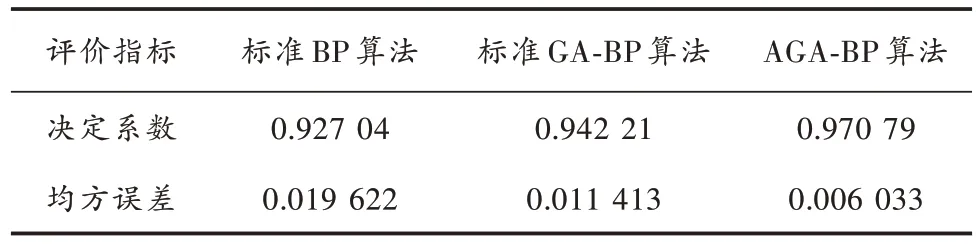
表4 网络性能比较
通过分析对比,AGA⁃BP 模型相对于BP 模型对卡钻事故的发生预测能力更好,准确性更高,泛化能力更佳,验证了本文模型的准确性。
3 结语
本文提出了一种基于自适应遗传算法的BP 神经网络卡钻事故预测模型。运用实际现场数据进行测试验证,结果表明该模型具有良好的预测能力,泛化能力佳,能够准确地处理钻井过程中复杂事故的非线性问题,为石油钻井过程中及时发现并处理卡钻事故提出了可行方案,具有一定参考意义。

