问题提出策略在高中数学教学中的应用实践探究

吴飞飞

(江苏省苏州实验中学 215011)

高中数学教学的本质就是不断给学生提出问题，然后解决问题的过程.在过去的高中数学教学中，主要以学生对数学公式、定理和法则的记忆为主，主要围绕课本内容展开.随着新课程改革的实施，学生的数学能力和数学思维的发展成为了数学教学的重要任务之一.在数学教学中，教师通过提出的问题，引导学生的思维，帮助学生掌握相应的知识，提高学生的数学能力，是当前数学教学的必要条件.问题提出教学策略要将学生的质疑和问题的提出结合起来贯穿数学课堂教学的始终，这就要求教师准确把握问题提出教学策略，能够准确把握什么时候提出什么问题，利用什么样的问题来促进数学教学.

一、问题的提出要遵循目标性原则

在高中数学课堂教学中，教师利用问题提出策略进行数学教学时，提出的问题要具有明确的目的，知道想要学生通过这一问题的提出达到什么样的学习效果，是激发学生的学习兴趣？还是引起学生对已有知识的回顾.另外，教师提出的问题，学生能够清晰地领会教师的意图，避免出现歧义和理解偏差.总之，问题的提出要以提高数学课堂教学的效果为目标，所有思维活动都要以此为中心展开.

例如，在“直线与方程”部分的教学中，教师可以这样通过问题提出策略开展数学教学，同时体现问题提出的目标性原则.

问题1：在前面的学习中我们学习了直线的相关知识，请同学们回忆一下，在平面直角坐标系中，确定一条直线的几何要素是什么？

通过这一问题的设计，帮助学生回忆前面学习的知识：“要确定一条直线需要知道直线的斜率和直线上的一点或者知道直线上的两点”，为接下来的学习奠定基础.

教师总结：要在平面直角坐标系中确定一条直线，需要知道定点的坐标(x0,y0)和斜率k，或者知道两个定点坐标P1(x1，y1)和P2(x2，y2).

问题2：那么直线上所有点的坐标(x,y)满足的关系，都能够通过上边的条件表示出来吗？

通过这一问题的设计，帮助学生进入本节课要学习的知识——直线方程.

二、问题的提出要遵循启发性原则

在数学教学中，提出问题的根本在于引导学生的思维，让学生跟着教师的思路去积极思考，因此，问题提出要具有启发性，通过适当的帮助和指导，提高学生的数学学习效果.借助启发性的问题，不仅能够引导学生解决数学问题，还能够将数学思想融入其中，提高学生数学解题能力.需要注意的是，提出的问题要略高于目前学生的知识水平，注意引导学生分析问题的本质，通过学生的积极思考以后，再对学生进行启发引导.

例如，在“椭圆”部分的教学中，教师可以这样来使用问题提出策略，不仅能够积极地引导学生的思维，还能够体现出问题提出的启发性.

问题1：题目中要求我们求椭圆的标准方程，我们需要知道哪些具体的量才能够求出椭圆的标准方程？

学生思考：需要知道焦点坐标和a，b的值.

通过这一问题的提出，能够给学生的阶梯思考提供方向，让学生能够进行有效的思维活动.

问题2：在题目的条件中，给出了焦点的坐标，我们通过焦点坐标能够得到什么有用的信息呢？

学生思考：能够得到c=2，且焦点在x轴上.

问题3：通过上述分析，我们知道了焦点位置和c的值，我们接下来能够怎么办？

学生思考：设出椭圆的标准方程，并且a2=b2+4

问题4：那我们如何求出所设标准方程中a，b的值呢？

通过以上一系列问题的提出，引导学生的思维，帮助学生建立了椭圆标准方程的一般解题模型.

问题5：大家思考一下，除了以上这种方法来求椭圆的标准方程以外，还有别的方法吗？

问题6：题目中给出了点的坐标，除了直接代入标准方程，通过解方程组获得a,b的值求椭圆的标准方程以外，我们还可以怎么利用？

学生思考：椭圆上任意一点到两个焦点的距离和都是2a，那么就可以根据距离公式得出2a的数值，然后根据c=2，求出b的值，进而求出椭圆的标准方程.

通过问题5的提出，能够对学生的思维做进一步的提高，引导学生做深入的思考.问题6的提出，为学生对问题5的思考指明了方向，起到了积极地启发作用.

问题7：通过两种方法的使用，同学们感觉哪种方法来求椭圆的标准方程更加简单？

通过这一问题的提出，来引导学生总结数学解题方法，帮助学生理解椭圆方程的本质.

三、问题的提出要遵循探索性原则

在高中数学课堂教学中，教师要能够通过好的问题来提高数学课堂教学的效果，具体来说，教师提出的问题要在现有学生认知水平的基础上，激发学生的探究兴趣，引发学生的讨论，并且这种讨论的结果不是唯一的，这样的问题设计才具有探索性.因此，数学教师提出的数学问题，难度要由浅入深，学生能够通过思考获得胜利的信心，提高自身参与探究的积极性，进而高效的建立起相应的知识体系.

例如，在“椭圆”部分的教学中，可以提出下列问题来引导学生的探究活动.

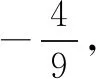
图1

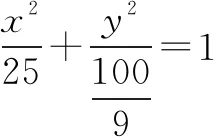
学生通过问题1的思考后，再分析问题2的时候能够非常容易的得出结果，提高了学生探究问题的积极性.

通过这三个问题的连续提出，难度一步一步增加，从特殊到一般，帮助学生借助提出的问题一步一步探索问题.

问题6：已知AB是圆的一条直径，M是该圆上不与A、B重合的任意一点，如果直线AM和直线BM的斜率均存在，那么直线AM和直线BM斜率的乘积是多少？

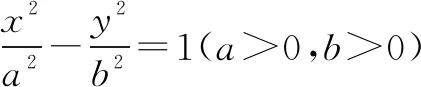
通过这两个问题的提出，学生在类比椭圆结论的基础上，分别探究出了圆和双曲线的相关结论，从而为帮助学生进一步探究一般化结论奠定了基础.

问题提出策略的使用，能够有效调动学生在数学课堂教学中的积极性，提高数学课堂教学的效果.因此，高质量的问题提出非常关键，作为高中数学教师，要不断加强数学自身素养的提升，提升自身设计优秀数学问题的能力，为数学课堂高效教学奠定基础.