问题巧转化 导数妙破解——一道含参不等式恒成立问题的探究

李彦彦

(甘肃省酒泉市瓜州县第一中学 736100)

不等式中的恒成立问题能够很好地考查函数、不等式等知识以及化归与转化等数学思想，一直备受命题者青睐，是各级各类考试中的热点问题之一.特别是涉及多个参数的不等式恒成立问题时，往往难度较大，让人无从下手，而且此类问题有时表现比较隐蔽，不易分辨，切入点不易发现.而导数作为解决不等式恒成立问题的有效工具之一，可以很好地破解不等式中的恒成立问题.

一、问题呈现

本题题目看似简单，但参数较多，综合含参数的一次函数与对数函数问题，不等式的恒成立以及代数关系式的最值问题等，内容丰富.如何通过含参不等式在定义域内的恒成立问题的转化，进而得以确定两相应参数k与b的比值的最值是解决问题的关键，而正确构造或转化为相应的函数模型，利用导数方法来求解相应函数的最值是解决问题的突破口.

二、多解思维

思维角度1(构造函数转化法1)根据题目条件，通过移项得到kx+b-ln(x+2)≥0，两次把相应的不等式恒成立问题转化为对应的函数的最值问题，通过求导，结合函数的单调性来确定其相应的最值，进而得到对应参数的比值的最小值.

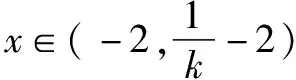
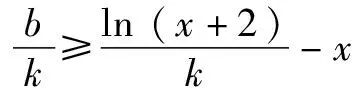
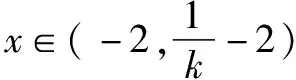
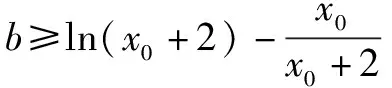
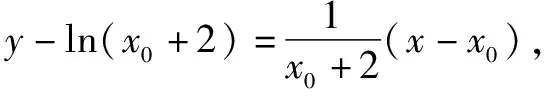
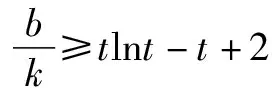
思维角度4(特殊值法)根据题目条件，由于kx+b≥ln(x+2)对于x>-2恒成立，通过选取特殊值x=-1代入对应的不等式，通过不等式的恒等变换得以确定k≤b，进而得到对应参数的比值的最小值.此类方法可以达到“秒杀”的功效，但方法不具有科学性，有一定的投机取巧之嫌.

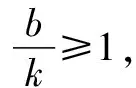
导数作为一种基本数学工具，可以用来处理与函数、不等式以及其他与之有关的很多问题，其中不等式的恒成立问题是其中最具有创新应用的一种.利用导数解决问题的实质是抓住用导数判断函数单调性的应用来处理对应函数的单调性问题，从而再转化为对应的不等式成立问题，巧妙转化，综合应用.