基于B-S样条下的半参数可加保序模型的性质
温美沙,王晓光,刘晓洁,杨 静,李珍珍,屈文欢
(1.河北北方学院 理学院 统计系,河北 张家口 075031;2.大连理工大学 数学科学学院,辽宁 大连 116024)
在目前快速发展的大数据时代中,现有的数据模型已经无法满足实践中遇到的一些测量问题,限制了现代科学技术在数据模型上的应用和发展。数据的可得性和多样性使得样本量无限增大,变量个数无限增多,从而对分析大数据特点有了新要求。例如说克服“维数灾难”,即解释变量的个数增多时,可以消除迅速增加的误差导致模型的拟合效果大大降低的现象。统计学家在寻找既能达到数据降维,又能保留非参数光滑优点的方法上,提出了多种降维的方法,把半参数可加模型中的非参数部分写成加法结构就是降维的一种方法。学者对半参数回归模型已有全面的研究,如:柴根象[1]给出了半参数可加回归模型中参数α和非参函数g的估计,薛留根[2]研究了半参数回归模型的两阶段估计的渐近性质,代金辉[3]在范数约束下给出了半参数回归模型参数估计及性质等。
半参数可加回归模型:
(1)
其中Z=(1,Z1,……,Zd)′和X=(X1,…,XJ)′分别是参数部分和非参数部分的随机向量,m1(·),m2(·),…,mJ(·)是未知光滑的单调递增函数,β=(β0,β1,…,βd)′是未知参数向量且属于某个凸集β∈d+1,E(ε|Z,X)=0和Var(ε)=σ2。 对于模型(1),当J=1时,Huang[4]通过使用最小二乘的方法给出了参数部分的估计量是渐近正态的,且非参数函数的估计量在随机向量X取某个固定值时是相合,其中保序估计量的性质不受参数项引进的影响。当J>1时,Cheng[5]基于池相邻惩罚准则研究了模型(1)的非参数函数的估计量也是相合。这篇文章对模型(1)的非参数部分使用带有保序约束条件的Bernstein-Schoenberg(B-S)样条[6]来逼近,从而估计其样条的系数来对非参函数进行估计,然后再用最小二乘法估计参数部分。
1 方 法

(2)
对于某个xj,可以写成
其中αj是L+k+1维的向量,bj(xj)=(b-k,j(xj),…,bL,j(xj))′是B-S样条基函数。存在1个对B-S样条的保序约束,在这样的约束下,对于任意的l=-k+1,…,L,对系数向量αj进行限制约束,使函数mj(xj)是单调递增的,即找到1个(L+k)×(L+k+1)的矩阵A,使得Aαj≥0,其中

因此,在Aαj≥0的条件下,式(2)的极小化问题等价于找β和αj的值,使得式(3)
(3)
2 模型的性质及其证明

(S1)E(Z-E(Z|X))⊗2恒为正定阵,对任意的向量V∈Rd, 我们定义外积V⊗2为VV′。
(S2)E(exp(γ|ε|))
(S3)函数mj满足
C1、α恒为正数。
(S4)假设Xj的密度函数PXj是有界的且满足Lipschitz条件
C2、ρ是常数。
(S5)函数ζj(Xj)=E(Z|Xj=x)满足条件
‖ζj(x)-ζj(x′)‖2≤C3|x-x′|
C3是常数。


基于上述6条假设,可以得到定理1和定理2。
定理1假设条件(S1)和(S2)成立,给定欧式范数‖.‖2,则有
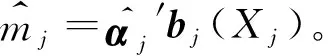
证明令xj(i)是Xj(i)的观察值,且Xj(i)是顺序统计量,即
Xj(i)={Xj∈[0,1]:mj(Xj(i))=(mj(Xj))i}
第一步,我们要证明(4)式成立。
(4)
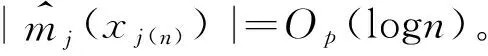
联合
bj(xj)=(b-k,j(xj),…,bL,j(xj))′,j=1,…,J

其中h是常数。因此,我们给出了下列不等式
其中C5,C6为有限正数。因此,证明式(4)成立。
第二步,我们要证明下面不等式成立。
(5)
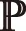
(6)

式(5)的右边
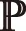
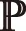
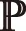
(7)

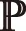
(8)
由式(6)、(7)和(8),证明式(5)成立。
第三步,给出一个函数族


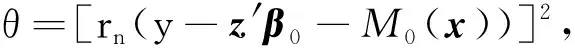
=-P[rn(ε+z′(β0-β)+(M0-M)(x))]2+P(rnε)2
=-P[rn(z′(β0-β)+(M0-M)(x))]2
=-P(θ-θn)2>-δ2




(9)
(10)
所决定。根据式子(5),我们知道
P[rn(z′(β0-β)+(M0-M)(x))]2≤δ2
(11)
最后,就L2(P)范数,研究Fn的δ-括号熵。因为Fn中的函数是关于(β,G(·))的二次方程,则Fn的δ-括号熵与G的一样。由参考文献[10]的推论1.3,我们知道G的δ-括号熵与1/ε同阶,因此Fn的δ-括号熵也与1/ε同阶。所以不等式(9)存在某个最小值,使得其等号成立,并且通过计算得到δ~n1/3。根据熵的变化,得到
(12)
其中β0是初始值,m0j(·)是初始函数。由于Z的有界性,不等式(4)进一步得到
(13)
结合式子(13)的下界,有
(14)
和
(15)
式子(15)暗示了
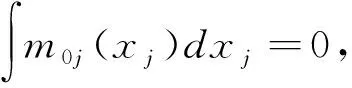
由此,推出
假设X的密度函数是小于无穷且有界的。因此就证明了定理1。
定理2如果条件S2-S6成立且向量X是两两相互独立的,就有
(16)


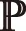
由于上述的等式及ε的独立性,我们就能推出

(17)

(18)
其中

和
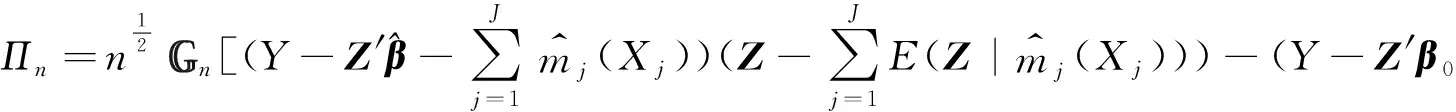
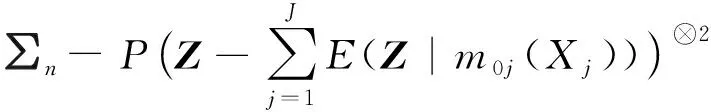


最后,通过参考文献[10]的引理5.13给出∏n的讨论。与本文定理1的证明类似,先给出函数族
其中rn=(logn)-1,g由上述所定义。

结合上述∑n,Δn和Πn的分析,首先对等式(18)的右端第一项应用中心极限定理,证得它是服从正态分布的。然后再对整个等式(18)应用Slutsky定理。证得定理2成立。
3 主要结论


