基于混合演化规则下的零行列式策略演化研究

赵 倩，毛雅俊

(1. 电子科技大学互联网科学中心 成都 611731)

合作行为在自然界和社会中广泛存在，极大地促进了物种的进化和人类社会的发展。但是自私个体永远在追求将自身利益最大化，利他行为与达尔文的进化理论相矛盾，因此如何令合作在自私个体之间涌现和维持受到众多领域学者的关注[1-3]。演化博弈理论为研究和解释这一现象提供了有力的理论支持，其中囚徒困境博弈是描述个体之间博弈行为的经典博弈模型之一[4-5]。捐助博弈是一个特殊的囚徒困境博弈模型，它描述了这样一个场景，参与个体会在博弈开始时选择合作(捐赠一个成本c)或者背叛(不捐助)。如果一方选择合作，她的对手将获得一个收益b；反之，她的对手将不会有任何收益。因此双方都选择合作的情况下，每个个体的收益都为R=b-c；如果双方都选择背叛(不捐助)会使得双方收益为P= 0。如果一方合作而另一方背叛，合作者将获得损失S= -c，而背叛者会获得T=b的收益。在捐助博弈中b＞c＞0，因此收益关系为T＞R＞P＞S，并且2R＞T+S。因此在没有额外因素的干扰下，参与囚徒困境博弈的理性个体为了最大化自己的利益总是会选择背叛。为了研究重复囚徒困境博弈中合作行为的演化，众多策略被研究和讨论，如“赢存输去”策略(win stay, lost shift, WSLS)、全合作策略、全背叛策略等[6]。但是这些策略都不能单方面决定对手的收益。2012年，文献[7]发现在重复囚徒困境博弈中存在一种特殊的一步记忆策略集合，名为零行列式策略(zero-determinant strategy)。这种策略能够单方面地限制双方的期望收益满足线性关系，而不限定对手的策略。随后学者们发现在雪堆博弈和公共品博弈中都存在类似的零行列式策略能够单方面控制参与博弈的个体之间的收益关系[8-9]。零行列式策略的发现揭示了博弈策略与期望收益之间的关系，并为研究一步记忆策略提供了新的思路。其中剥削策略最为引人关注，它总是能够获得不低于对手的收益。然而剥削策略与背叛策略博弈时，双方的收益都为P，很容易受到背叛者入侵，因此它在种群演化中是演化不稳定的，但是它能够促进合作策略在种群中的涌现[10-11]。

在经典的演化博弈论中通常假设个体之间的交互是均匀混合的，即所有个体全部连接。但是现实社会中，个体之间的连接数是有限的，每个个体仅仅与周围少数个体接触。1992年，文献[12]发现在二维方格网络上，个体在与直接相邻的4个邻居进行博弈时，合作者可以出现并稳定存在，并且合作者可以通过结成合作簇的形式来抵抗背叛者的入侵。这一发现首次指出了网络结构对于博弈演化的重要作用，网络互惠也被认为是促进合作演化的一类重要机制。随着复杂网络理论研究的新兴，小世界、无标度等网络特性被证明对网络中合作的涌现带来了极大的影响[13-15]。并且学者们发现引入剥削策略可以在规则网络和无标度网络上形成“合作-剥削联盟”来抵抗背叛策略的入侵，从而促使合作策略的涌现[16-20]。

在网络演化博弈中，不仅仅是网络结构会影响合作的演化结果，演化规则也起到了至关重要的作用。演化规则是指个体期望获得更高收益而更新自身策略的规则。通常网络中的个体会通过比较自身与周围邻居的收益差，从而模仿邻居的策略不断将自己的收益最大化。演化规则也是刻画复杂网络上演化动力学的关键因素。各种不同的更新规则通过仿照自然或者是社会个体决策过程而被提出，由生物进化而演变来的最基本的策略演化规则如复制动力学[21]，费米动力学[22]和Moran过程[9]等。随后一种类似于“赢则坚守，输则变通”的个体策略演化规则被提出[23]，在这种规则中，网络上的每个个体将不再与邻居的收益对比，它会比较实际所获得的收益与期望收益，并根据收益差以费米函数形式获得概率选取下一轮的策略。在这些演化规则中，所有个体仅仅会考虑一种演化规则更新策略。但是在现实世界中个体改变自身策略并不是一成不变的。当它当前的策略所能获得的收益低于邻居的收益时，它将会模仿邻居的策略，但是当自身收益高于邻居时，为了最大化自己的收益，个体将会采取不同的演化规则。一些混合演化规则应运而生，例如部分个体进行复制动力学更新，其他根据期望更新策略[24]；或者个体以一个固定概率进行复制动力学更新否则根据期望更新[25]；也有将两种更新规则相结合的混合演化规则[26]，以及一些其他混合演化规则[27-30]。

本文基于复制-期望的混合演化规则，研究剥削策略、合作策略与背叛策略在方格网络上的演化，探索剥削策略对方格网络上合作的影响。通过蒙特卡洛仿真比较混合演化规则下的3种策略的稳态比例，并从微观角度分析和对比了复制动力学演化规则下与混合演化规则下剥削策略在演化过程对合作的影响和作用，最后讨论了剥削系数以及背叛诱惑对网络中合作策略稳态比例的影响。

1 模型描述

1.1 捐助博弈中的剥削策略

根据文献[7]可知，在重复囚徒困境博弈模型中，当一个采用剥削策略E的个体与另一个体Z进行博弈时，双方的期望收益可以表示为：

式中，PE、PZ分别代表了剥削者和对手的期望收益，可以看出它们之间满足线性关系。并且剥削系数的范围为sE∈(0,1)。 当P=0时，剥削者总是能获得对手1/sE倍的收益。

由此可知合作策略C、背叛策略D和剥削策略E这3种策略之间的收益关系如表1所示。

表1 3种策略的收益

通过表1可以看出，合作者可以从与剥削者的博弈中获得少量大于0的收益，而剥削者从合作者的博弈中获得了少于b的收益。并且在sE的取值范围中，随着剥削系数sE的增加，合作者的收益越大，剥削者的收益会减少。而且，剥削策略与背叛策略之间的收益为0，双方不能从对方获得任何收益，因此剥削策略与背叛策略是中性漂移的关系。在本文中b－c=1，此时博弈模型中只存在一个可调参数即为背叛诱惑b。

1.2 复制-期望演化规则

个体之间的连接关系可以用复杂网络来描述，即网络中的节点代表了博弈个体，节点之间的连边代表两个个体之间存在博弈关系。初始时，网络中的个体X将随机从合作策略、背叛策略和剥削策略中选取一种策略，随后个体将会与自己的每个邻居进行捐助博弈并获得一个收益PX。在一轮博弈结束后，个体X将以概率

选择进行复制动力学更新，否则以概率1 -UX选择期望演化规则更新策略[18]。其中参数 β用以调节个体的选择不同演化规则的概率。当 β=0时，网络中个体将通过复制动力学更新自身策略。此时，个体X将随机选择一位自己的邻居Y，并以概率W学习Y的策略：

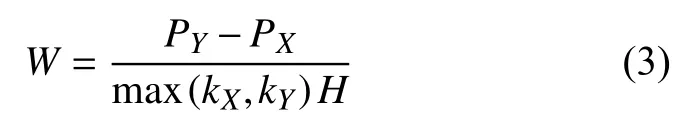
式中，kX、kY代表个体X、Y的度；H是两个个体之间可能存在的最大收益差，在本文中H=b+c。可以看出X学习Y的概率正比于双方的收益差，收益差越大，学习的概率越高。

当 β＞0时 ，网络中个体会以概率1 -UX通过期望演化规则更新策略。即个体更新策略时并不会与周围邻居比较，而是会有一个收益期望A，即个体对于环境的满意度。如果个体X的期望收益为PXA=kXA， 其中A是控制参数并且A∈[0,b-c]。那么个体X更新策略时，它将比较自身所获得的实际收益和期望收益，并以费米函数形式计算概率W选取策略更新：

这样当A越低，个体越容易满意当前的收益，而不会经常改变自身策略。但是当A较高时，个体常常不能满足自身期望而频繁改变自身策略。可以看出，当 β=0时，网络中所有的个体都将进行复制动力学更新，而当 β=0时，获得高于0收益的个体将采用期望演化规则更新自己的策略。κ是环境中的噪声因子，代表了个体的不理性程度。根据之前的研究，本文中设定κ = 0.1且A=0.1。

基于以上的博弈模型与更新规则，本文通过蒙特卡洛仿真方法对规模为100×100方格网络上的策略演化进行仿真。初始时，网络中的合作、背叛和敲诈的比例各占1/3。在每个时间步中，个体将与邻居进行博弈并根据收益矩阵获得收益，接着会根据混合更新规则更新自身策略。为保证系统进入稳态，演化过程会进行11万步的迭代，并计算最后1万步中3种策略所占比例的平均值作为最终结果。并且每个参数的结果都是运行独立重复10次仿真后的平均值。

2 实验结果及分析

图1依次展示了当网络中仅存在合作策略、背叛策略和剥削策略时，在混合演化规则下，随着背叛诱惑b的变化，合作者、背叛者和剥削者在网络中所占的稳态比例F。由演化规则可知，当β=0时，网络中的个体更新规则为复制动力学，演化结果如图1a所示。合作者仅仅能够在b＜1.09时在网络中稳定存在，并且此时网络中只有合作者与背叛者。当b较大时，合作策略在网络中灭亡，网络中只有剥削策略和背叛策略，此时剥削系数sE=0.5的剥削者不能促进网络中的合作行为。

图1 合作者、背叛者与剥削者在方格网络上基于混合演化规则下的稳态比例

当个体更新策略时采用 β=1的混合策略规则，如图1b所示，演化结果发生了显著的变化。合作者能够在网络中稳定存在，且当b=1.15时，网络中的合作者比例达到最大值。而剥削策略从消亡状态开始能够在网络中稳定存在，并且随着b的增加剥削者的比例也在上升。但是随着b的继续增大，合作者的比例逐渐减小并在b=1.85时完全消亡，此时网络中只存在剥削者与背叛者。上述结果说明，在混合演化规则下，剥削系数sE=0.5的剥削策略能够促进合作策略在网络中涌现。

接下来本文将通过对比在不同演化规则下策略的微观演化过程进一步解释混合演化规则是如何促进合作策略在网络中的涌现。图2展示了在sE=0.5，b=1.6的情况下，从策略演化、平均收益演化和策略对的演化3个角度来进行分析。在网络中合作、背叛和剥削这3种策略存在时，那么就有6种可能的策略对组合：合作-合作、合作-背叛、合作-剥削、背叛-背叛、背叛-剥削和剥削-剥削，这些策略对的比例可以刻画出个体由于邻居的影响而改变策略的情况。

图2 混合演化规则下，3种策略在网络中的策略比例、平均收益和不同策略对比例随时间的变化情况

图2a～2c展示了当 β=0时，所有个体采用复制动力学更新策略。初始时3种策略均匀地随机分布在方格网络上，每种策略所占网络的比例都为1/3。从图2a可以看出，合作策略被迅速入侵并在t=1000时刻消亡，网络仅仅剩下背叛策略和剥削策略。根据表1可知，背叛策略与剥削策略之间是中性漂移的关系，因此当合作策略消亡后，剥削策略与背叛策略的比例不会发生变化。3种策略在演化过程中的平均收益与策略对的变化情况如图2b和图2c所示，由于初始时3种策略随机分布，因此初始时合作者的收益要低于剥削者与背叛者的收益。所以大量的合作者转为剥削者或者背叛者，也导致包含合作策略的策略对，即合作-背叛、合作-剥削与合作-合作策略对快速减少。孤立的合作者被迅速入侵，合作者只有形成合作策略簇才能获得较高收益。此时合作者的平均收益要高于剥削者和背叛者，这是由于合作-合作策略对的存在提升了合作者的收益。但是合作策略并不能稳定存在，由于合作-背叛与合作-剥削策略对存在，使得与合作者为邻居的剥削者和背叛者获得更高的收益，从而入侵了合作簇。随着合作-合作策略对的比例下降，每个合作者将有更多的非合作者为邻居，合作策略的收益会变为负数，从而导致了合作者的消亡。

图2d～2f展示了引入期望更新的混合演化规则(β =1)的情况。即当个体收益大于0时，它在更新策略时就会以概率UX选择复制动力学更新，反之会以期望演化规则更新策略。同样从策略比例、策略对比例与平均收益3个方面来说明。由于初始时的个体随机分配策略，每个策略都会以相同概率遭遇其他策略。背叛者的平均收益要高于剥削者，而合作者的收益最低。因此合作者被其他两种策略入侵，合作者的比例迅速下降。与β =0的情况不同的是，合作者并不会就此消亡。从图2d可以看出，合作者会在t=100时刻以一个小概率维持在网络中，随后开始爆发，并且能够在网络中稳定存在。从图2e可知，这是因为在合作者比例降低的同时，背叛者与剥削者的收益开始下降，不同于单纯的复制动力学演化，此时策略的收益都大于0，他们都存在概率进行期望更新。而且剥削策略与背叛策略之间的收益都为0，并且剥削者所能从合作者得到的收益要小于背叛者获得的收益，此时剥削者的收益将小于自身的期望收益。在这种情况下剥削策略将会转为合作策略，从而增加了网络中合作者的数量。结合图2f中策略对的演化可知，在t＜100时合作者所组成的策略对比例下降，其他策略对的比例都有所上升。但在t＞100后，合作-剥削与合作-合作的策略对比例开始上升，但是合作-背叛策略对的变化较小。说明拥有合作者邻居的剥削者率先转变为合作者，而后合作者形成合作簇。且由于剥削策略与背叛策略之间的收益为0，背叛者不能入侵剥削者，反而是拥有合作者为邻居的背叛者获得高收益从而入侵了背叛者。所以合作者的比例开始上升并能够在网络中稳定存在，根据以上分析可以得出，混合演化规则可以促使“合作-剥削联盟”在方格网络中的扩散，从而促进了合作行为的涌现。

接下来，图3进一步展示了当b=1.6，sE=0.5的情况下，3种策略基于混合演化规则更新策略时，不同时刻在方格网络上的分布情况。每个点代表一个个体，其中黑色为合作者，灰色为背叛者，白色为剥削者。当个体随机的选取策略时，各种策略混杂的分布在网络中。经过几轮的演化后，合作者被入侵，网络中大部分个体被背叛者和剥削者占领，合作者只能通过簇的结构维持少量的比例分布。在图4a中，由于 β=0，合作者不断被侵蚀，最后消失在网络中。然而，当引入混合演化规则后，剥削者将不满足于当前的收益而改变自身的策略，而这些剥削者通常有合作者作为邻居，从而能够容易的形成合作簇。此时大部分的合作簇被包裹在剥削者所组成的罩子中，这样更加便利地促成了“合作-剥削联盟”，帮助合作行为在网络中涌现和维持。对比图3a和图3b可以看到，在相同的时间步当中，混合演化规则能够帮助合作策略形成合作簇，且这些合作簇都被剥削策略包围。此时背叛策略不能接触更多的合作者，从而抵制了背叛策略的入侵，使合作策略能够在网络中存活下来。

图3 在混合演化规则下t=1、100、1 000和100 000时刻方格网络上不同策略的分布斑图

以上研究证明了在混合演化规则下，通过零行列式策略的引入，形成有效的“合作-剥削联盟”帮助合作策略，更好地建立了合作簇，从而有效地提升了网络中的合作者比例。最后，本文研究了不同sE-b取值对于网络中合作策略稳态比例的影响。图4以热力图的形式展示在不同sE-b取值下合作者的稳态比例。首先当β =0时，随着b值的升高，合作者的比例不断下降。sE对于合作涌现存在非单调的影响，只有sE∈(0.1,0.3)的范围内时，合作行为被最大程度地促进了。当sE＞0.3，合作策略不能在b＞1.1稳定存活。而当个体按照混合演化规则更新时，明显看出当网络引入 0.1＜sE＜0.5范围内的剥削策略，都能使合作行为在网络中稳定存在。当sE=0.4时，合作者在方格网络上的比例达到最大。且相较于个体单纯采用复制动力学的结果，混合演化规则不仅使拥有高剥削系数的剥削策略促进了合作行为的涌现，并且此时网络中的合作者比例更高，证明了复制-期望演化规则下，剥削策略促进了方格网络中合作行为的涌现。

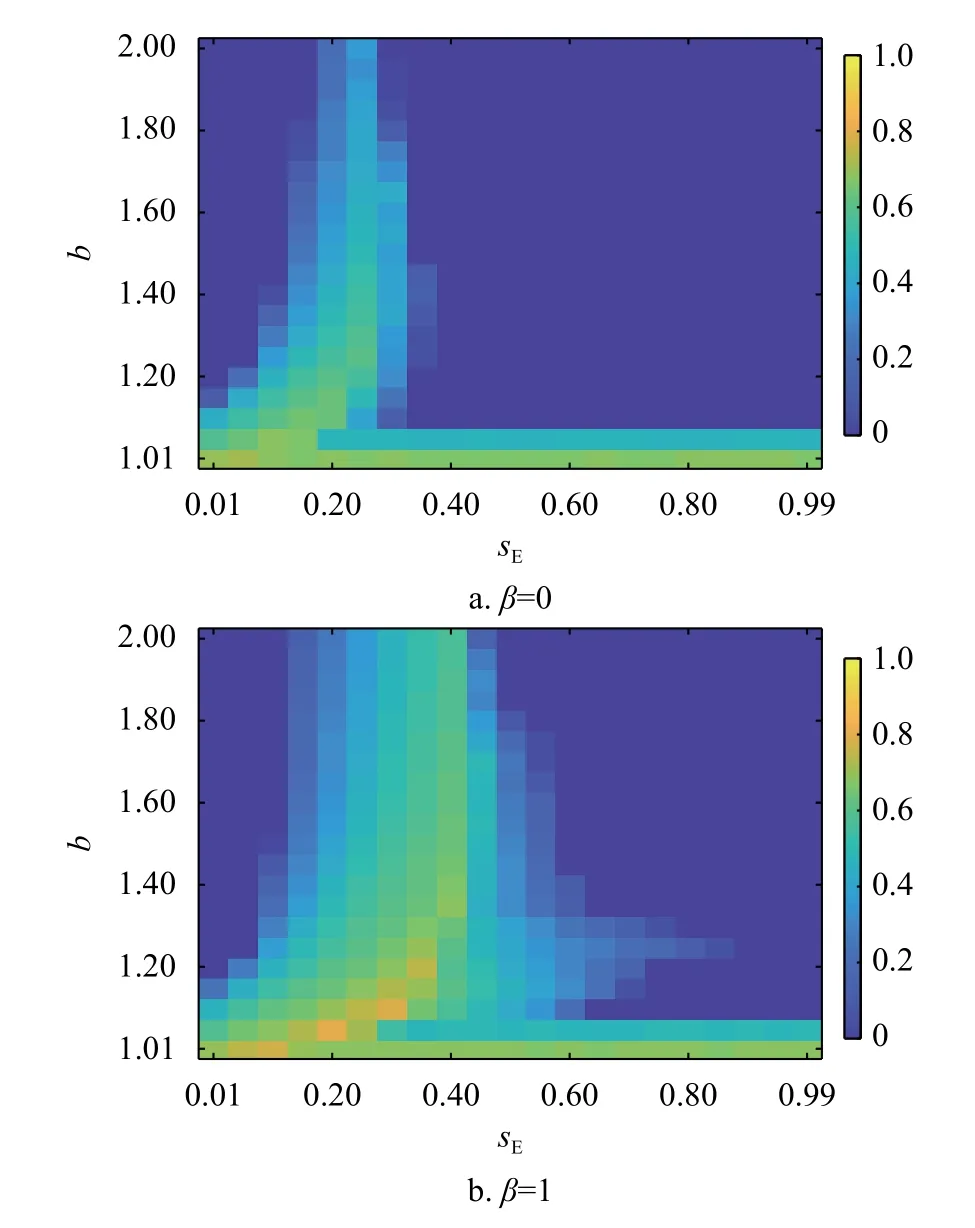
图4 混合演化规则下不同sE-b取值对方格网络上合作策略稳态比例的影响。

3 结 束 语

零行列式策略的发现丰富了博弈中的策略空间，并通过马尔科夫随机过程揭示了博弈策略与期望收益之间的关系，为博弈论的研究和发展提供了重要的理论框架。其中剥削策略能够作为催化剂和屏障促使合作策略的涌现与维持，因此受到了广泛的关注。

网络互惠作为促进合作涌现的重要机制，研究了网络结构、策略演化和网络模型之间的关系。本文基于复制-期望演化规则，探讨了在引入剥削策略后，合作策略、背叛策略与剥削策略在方格网络上的演化动力学。虽然较大剥削系数的剥削策略无法在复制动力学规则下促进合作行为在网络中的涌现，但是在混合演化规则下，这些剥削策略能够形成稳定的“合作-剥削联盟”，从而帮助合作行为在网络中能够稳定存在。通过对比不同的演化规则的微观过程，本文发现，混合演化规则可以通过期望收益的内驱动力驱使剥削者向合作者转变，从而促使合作簇的形成与“合作-剥削联盟”的稳定存在。通过研究sE-b取值对方格网络上合作策略稳态比例的影响，本文发现在混合演化规则下，剥削系数对于合作策略的促进作用依然是非单调的。本文对于进一步理解剥削策略在真实场景中的演化作用，以及如何促进复杂系统中合作的涌现提供了新的思路。