周期场驱动下量子材料的非平衡物态*
王恩 董文翰 周辉 刘猛 纪洪艳 孟胜 孙家涛†
1) (中国科学院物理研究所, 北京凝聚态物理国家研究中心, 北京 100190)
2) (北京理工大学信息与电子学院, 低维量子结构与器件工信部重点实验室, 北京 100081)
3) (中国科学院大学物理科学学院, 北京 100049)
量子材料的拓扑物态的研究是当前凝聚态物理的重要前沿.区别于局域对称性破缺对物质状态进行分类的传统方式, 量子物态可以用微观体系波函数的拓扑结构进行分类.这些全新的拓扑物态有望颠覆传统的微电子学并进而推动拓扑电子学的迅猛发展.当前大部分理论和实验研究集中于研究量子材料的平衡态性质.周期性光场驱动下量子材料远离平衡态、而达到非平衡态时的拓扑物态近年来受到人们的广泛关注.本文首先回顾周期场驱动下非平衡态的弗洛凯(Floquet)理论方法, 分别介绍无质量(如石墨烯)、有质量(如MoS2)等狄拉克费米子材料体系在远离平衡态下的拓扑物态, 利用光场与量子物态的相干耦合实现对量子材料非平衡物态的调控; 从原子制造角度出发, 光场诱导的相干声子态直接改变了量子材料中电子跃迁的大小, 进而调控量子材料的非平衡拓扑物态.量子材料中丰富的声子态为非平衡拓扑物态的调控提供了更多的可能性.最后, 文章展望了量子材料非平衡拓扑物态在超快相变以及瞬态物态调节等未来可能发展方向的应用.
1 引 言
拓扑物态是凝聚态物理的重要前沿领域.这方面研究的快速发展已经有近二十年, 涉及到的量子材料体系有拓扑绝缘体[1–7]、拓扑半金属[8–14]、以及拓扑超导体[15–17]等等.人们对拓扑相的研究已经几乎有了完整细致的分类和系统表征[18], 例如近年来出现的高阶拓扑物态等[19–21].过去的这些研究大多集中在静态的量子系统, 当其受到较小绝热微扰时体系的能隙不闭合, 体系的拓扑物态不随外界条件改变, 即没有外场响应.近年来人们发现利用光与物质的耦合, 可以驱动量子材料远离平衡态并使其发生拓扑相变.这些非平衡态体系的研究方法用弗洛凯理论来描述.周期场驱动引入时间这一独特的自由度, 不仅实现平衡态下无法得到的弗洛凯非平衡态[15,22–25], 甚至实现静态量子材料完全不具备的新型拓扑物态, 将非拓扑性的量子材料转变为具有新型拓扑物性[26–30], 如弗洛凯版本的马约拉纳费米子[31–35], 拓扑超导体[32,35,36], 拓扑绝缘体以及陈绝缘体等[37].此时传统的体边对应关系可能不再适用, 陈数为零的能带之间也可能存在反常的拓扑边界态[38,39].这些新奇的量子物态在超快自旋电子学[40]、谷电子学[41–43]、拓扑电子学[44]、拓扑量子计算[45]等方面都具有非常重要的研究意义.
为了表征和调控量子材料的拓扑物态, 人们发展了多种实验技术手段[46].其中泵浦-探测实验技术可以在时间、空间以及能量自由度上进行高分辨率的表征.通过调节光子能量, 光场强度, 极化方向等多自由度实现激光与量子材料的本征电子态产生耦合.比如当飞秒激光光场脉冲持续时间远小于晶格振动模式的振动周期, 光子的相干性将传递给晶格的集体振动, 并引起声子的共振激发, 这种由于光子相位相干引起的原子集体运动, 可称作相干声子[40,47,48].原子集体振动修饰后的电子已经不同于未被修饰的电子, 此时电子被认为是准粒子.除了平衡态的能带结构, 电子能带结构呈现出多重被修饰的复制的能带, 也称为弗洛凯边带, 由弗洛凯理论来描述.声子修饰后的电子能带结构可以利用时间分辨和角度分辨光电子能谱(time-resolved and angle-resolved photoemission spectroscopy,Tr-ARPES)探测.其非平衡拓扑物态可通过类似平衡态的基本概念来描述.相干声子的产生和探测不仅为研究量子材料中光与物质耦合的基本物理提供了机遇, 同时为超快时间尺度下操控量子材料的动力学特性, 如铁电结构相变[49]、瞬态增强的超导特性[50,51]、光致磁性耦合[52,53]等提供了新的机制, 为原子制造提供了新的可能.
费米子和玻色子体系中均可实现弗洛凯系统.近年来冷原子光晶格技术的发展, 促使人们去发现和构造全新的拓扑相[54,55]以及诸如时间晶体[22,23]等特殊系统.人们可以利用激光控制冷原子相互作用实现周期性驱动光晶格模型[56].通过对势场或者相互作用强度进行调控, 能够实现物理上等效的弗洛凯模型[57–60].在玻色子体系如光子晶体中, 一方面通过微波等调控手段, 可以直接实现弗洛凯系统[61].另一方面, 对于由螺旋状波导构成的光子晶体, 其沿螺旋轴方向光场传输行为与随时间演化效果等同, 亦能在静态系统中实现等效周期性外场调制[26,38,62,63], 见图1深蓝色区域.
利用周期场驱动量子材料达到非平衡态的调控被称为弗洛凯工程.由于增加了时间维度, 系统对称性变得更为丰富, 弗洛凯系统中拓扑相分类亦变得更为丰富[24,25,55,64–66], 有可能调控得到高阶拓扑特性[36,67].对于拓扑半金属体系而言, 无能隙线性色散能带决定了其低能激发行为.利用外加光场, 人们既可以实现量子材料能隙的打开和关闭,也可以调控狄拉克锥或外尔锥的倾斜度[68,69].圆偏光打破了系统的时间反演对称性, 而线偏光则破缺了体系的空间旋转对称性, 由此可能导致体系序参量发生变化, 出现光诱导超导现象以及马约拉纳态[32].可以预期, 弗洛凯系统能够与超快自旋电子学[70,71]、谷电子学、光电子学等相结合, 进一步拓展弗洛凯工程的应用范围, 见图1绿色区域.

图1 弗洛凯工程研究框架示意图.深蓝区域代表被驱动体系, 如玻色子系统、费米子系统等; 红色区域代表狄拉克以及外尔半金属、马约拉纳费米子、拓扑界面态等非平衡拓扑物态; 绿色区域代表弗洛凯工程在超快自旋电子学、谷电子学、瞬态超导特性、斯格明子等方面存在潜在应用.图片素材来自文献[31, 39, 62, 68, 70, 71]Fig.1.The schematic of the research framework of Floquet Engineering.The deep blue region denotes driven system including bosonic and fermionic system.The red region denotes the nonequilibrium states such as Dirac and Weyl semimetals, Majorana Fermions, topologically nontrivial interface states etc.And the green regions denotes the potential applications of Floquet engineering in ultrafast spintronics, valleytronics, transient superconductivity, Skyrmions etc.The pictures are adapted from Refs.[31, 39, 62, 68,70, 71].
本文将在量子材料的非平衡拓扑物态及其调控方面进行概述.首先介绍弗洛凯工程包含的基本内容, 简要介绍弗洛凯定理的基本内容及其拓扑物态计算方法; 其次分别介绍周期场驱动下无质量和有质量狄拉克费米子以及狄拉克节线半金属的拓扑能带结构的演化; 然后从原子制造的角度出发介绍利用弗洛凯定理研究相干声子对量子材料非平衡拓扑物态的影响; 最后对未来可能的研究方向给出展望.本文对从事量子材料的动力学理论和超快光谱实验的研究人员均具有一定的参考价值.
2 弗洛凯定理及其非平衡态的计算方法
本节简要介绍如何描述周期场驱动下的弗洛凯系统.在数学上, Floquet[72]在1883年证明了对于一阶线性常微分方程如果A(t) 是周期为T的连续周期函数, 那么其基本解的形式为x(t)=Q(t)exp(tK),Q(t+2T)=Q(t).这 被 称为弗洛凯定理.对于含时量子系统, 其波函数演化遵循薛定谔方程

其中|Φ(t)〉 为系统波函数,为体系哈密顿量, 驱动周期T=2π/Ω.为了简单起见,本文约定 ℏ =1.根据上述弗洛凯定理, 方程(1)的解可以写为一个随时间变化的相因子和周期性函数的乘积[73]:
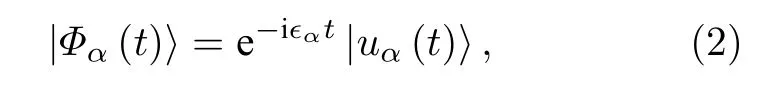
这里|Φα(t)〉 称为弗洛凯本征态, 周期性函数部分|uα(t+T)〉=|uα(t)〉 ,ϵα称为准能量.由于弗洛凯本征态是周期函数, 具有和系统哈密顿量相同的周期.假如系统具有空间平移对称性, 由布洛赫定理可以将薛定谔方程的解进一步写为布洛赫-弗洛凯态的形式:
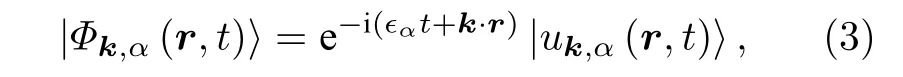
在弗洛凯系统中弗洛凯本征态之间的内积可以定义为一个驱动时间周期内对本征态波函数内积的平均[75–77]:

在上述内积定义下, 任意不相同的弗洛凯本征态之间两两正交,{|Φα(t)〉}构成一组正交归一完备基.通过本征态和内积定义, 所考察的随时间周期变化的电子波函数所张成的空间不再是原有的希尔伯特空间R, 而是广义希尔伯特空间R⊗T, 其中T代表时间周期函数构成的空间.
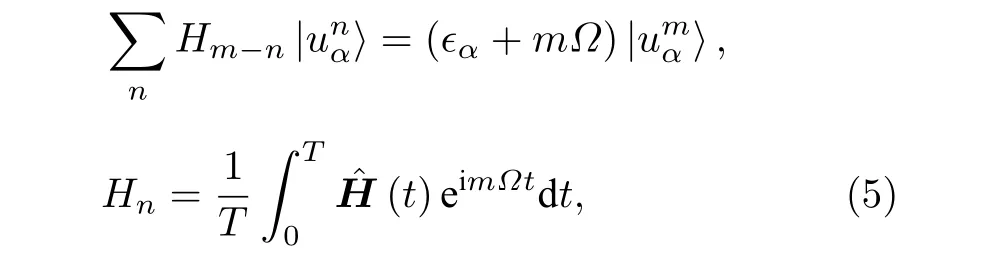
对应的矩阵形式为

定义 (HF)mn=Hm−n−mΩ·Ⅱ , 其中 Ⅱ 为单位矩阵,HF被称为弗洛凯哈密顿量.通过将含时的映射到时间无关的弗洛凯哈密顿量HF, 在周期性外场驱动下量子系统的动力学演化行为可以从准静态系统出发描述.在光场频率较高、强度较小的情况下, 截断后的弗洛凯哈密顿量矩阵[68]仅选取m= 0, ±1, ±2, 就可以较好地描述系统布洛赫-弗洛凯态的能带结构和波函数.如果从系统的时间演化算符U(t,t0) 出发, 在周期性外场驱动下, 系统波函数按照如下演化|Φ(t)〉=U(t,t0)|Φ(t0)〉.弗洛凯哈密顿量HF可以借由时间演化算符构造得到,eiHFT=U(T+t0,t0).从定义中可以看出,HF描述了弗洛凯系统在周期场驱动下的动力学演化行为.
除了矩阵截断方法外, 系统的有效弗洛凯哈密顿量可以通过微扰展开方法构建.在形式上, (6)式中的弗洛凯哈密顿量HF对系统周期T进行级数展开[78]:

利用Magnus展开[78–80], 可以得到在外场较弱、驱动频率较高的情况下的近似公式为[71,81–83]

反之在驱动频率较低的情况下, 同样可以使用微扰理论处理.回顾弗洛凯本征方程(5), 定义(H′)mn=Hm−n为非微扰意义下的哈密顿量, 这等价于直接将希尔伯特空间R中的电子波函数映射至广义希尔伯特空间R⊗T.

利用广义希尔伯特空间中的内积定义(4)式, 以及对薛定谔方程中弗洛凯态的周期性要求, 最终可以得到微扰展开至最近几阶的哈密顿量及其准能级和系统波函数.
为了直观展示弗洛凯哈密顿量与系统静态哈密顿量之间的相互关系, 以周期性光场驱动下的具有线性色散关系的体系为例(图2(a)), 求解弗洛凯本征值方程得到的弗洛凯-布洛赫能带如图2(b)所示.通过对弗洛凯系统进行傅里叶变换, 弗洛凯哈密顿量的对角元的形式和平衡态下哈密顿量相同.由于光场的引入, 使得体系本征态之间通过吸收和释放虚光子过程耦合在一起, 也对应矩阵表达式(6)式中的非对角元项, 并在多重能带的交叉点打开能隙, 如图2(c)所示.Mahmood等[84]利用泵浦-探测技术在Bi2Se3表面探测到了弗洛凯能带的线性色散特征, 如图2(d)所示.圆偏光打破了时间反演对称性, 在线性能带的交叉点处打开了能隙[85].

图2 (a) 在具有线性狄拉克锥的体系中施加圆偏光, 实现周期性外场驱动下的弗洛凯系统[71].(b) 弗洛凯系统中的能带结构和边带[71].(c) 弗洛凯系统能带结构起源示意图.每一个方框分别代表静态系统哈密顿量子空间, 由于光场的引入, 使得相邻子空间的本征态之间通过吸收和发射虚光子过程发生耦合, 对应矩阵表达式中的非对角元项 H ±1 , 更高阶非对角元则对应多光子过程.(d) 利用Tr-ARPES技术在Bi2Se3表面观察到的弗洛凯-布洛赫能带结构[84].其中颜色深浅代表对应光电子信号强度, 图中红色箭头表示能隙所在位置Fig.2.(a) Floquet system driven by a periodic external field can be created by imposing circularly polarized laser on a linear Dirac cone[71].(b) Energy band structure and energy band replica in Floquet systems[71].(c) Schematic diagram of the origin of the energy side band of the Floquet system.Each framework represents one subspace from the Hamiltonian of the static system.The light field make the original eigenstates of different subspace coupled together through the process of absorbing and emitting virtual photons,corresponding to the off-diagonal element like H ±n , n = 1.Other higher-order off-diagonal elements (n > 1) correspond to multiphoton processes.(d) Floquet-Bloch band structures of topologically nontrivial surface states on Bi2Se3 measured by Tr-ARPES[84].The magnitude of color bar denotes the intensity of photoemission signals.The red arrows denote the gap-opening regions.
除了弗洛凯系统中复制能带的基本特征以外,对诸如弗洛凯光电子能谱[86]、光学响应[87,88]、非线性位移电流[89]以及高次谐波[90,91]等可观测量的讨论也尤为重要; 而借助弗洛凯理论框架, 人们也讨论了多个频率外场驱动下非线性系统的动力学行为[92].受限于篇幅, 本文不对上述内容展开讨论.
3 无质量狄拉克锥体系中的弗洛凯系统
单层石墨烯是凝聚态物理领域中一个重要的模型体系.若仅考虑石墨烯中最近邻相互作用, 其能带在布里渊区K点和K'点具有线性色散的狄拉克锥[95].考察石墨烯在光场的作用下石墨烯的能带结构以及输运性质的变化.在单粒子近似下的紧束缚模型中, 只考虑蜂窝状格点之间pz轨道形成的π键之间的相互作用, 忽略电子-电子、电子-声子等其他相互作用的影响.石墨烯的静态哈密顿量为

其中t0为最近邻跃迁矩阵.(10)式引入矢势为A(t)=A(±sin(Ωt),cos(Ωt)) 的圆偏光, 其中Ω为光场频率.光场的强度可以用无量纲数A=Aa表示,a为石墨烯蜂窝状格子的晶格常数.为了简单起见, 约定光场的引入使得电子在跃迁时积累额外相位, 跃迁矩阵元从t0变为t0eiAij(t),其中Aij(t)=(rj−ri)·A(t) ,ri为第i个格点的位矢.从动量空间出发, 上述效应等价于将动量进行皮尔斯替换H(k)→H(k−A(t)).
当光场频率和跃迁能量不一致时, 光场并不直接激发电子跃迁, 而是通过吸收和释放虚光子的过程对能带进行修饰.如图3(a)所示, 在圆偏光作用下, 狄拉克锥对应打开能隙.Oka和Aoki[27]通过计算弗洛凯哈密顿量HF得到体系能隙大小为当外加光场较小时, 系统在狄拉克锥附近的有效哈密顿量为
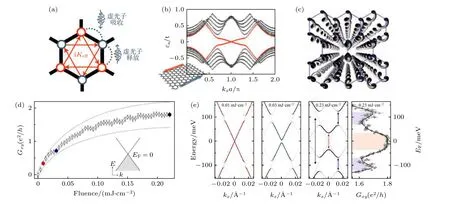
图3 (a) 蜂窝状晶格中的次近邻跃迁在施加圆偏光后对应虚光子的吸收和发射过程, 产生与Haldane模型类似的次近邻跃迁矩阵元[71]; (b) 施加圆偏光后石墨烯纳米带能带中的手性边缘态(红线)[93], 其在实空间对应两个边界上反向运动的手性边缘态(左下角插图); (c) 光子晶体中实现周期场驱动的弗洛凯系统[62]; (d) 利用泵浦-探测技术探测出现在石墨烯中的反常霍尔电导[94];(e) 在不同光场强度下弗洛凯-布洛赫能带图及能隙内的手性边缘态电导平台[94].图中红色、蓝色、黑色能带分别对应光场强度逐渐加大, 弗洛凯能隙亦逐渐增大.最后一张图对应光场大小为0.23 mJ/cm2时不同费米面位置对应接近量子化的电导平台, 反应了费米面附近的系统能隙为拓扑能隙Fig.3.(a) Laser irradiated honeycomb lattice have virtual photon absorption and emission processes.These effects lead to nextnearest-neighbor hoppings similar as that in Haldane model[71].(b) Band structures of laser irradiated graphene nanoribbon[93].The red lines in this panel denote the chiral edge states, which move along opposite directions of graphene nanoribbon edges (inset).(c) Photonic analog of laser irradiated honeycomb lattice[62].(d) The anomalous Hall conductance in laser irradiated graphene measured by pump-probe method[94].The sub-linear relationship between nearly quantized conductance and laser fluence has been observed.(e) Floquet band structure with different laser fluence[94].If increasing the laser fluence, the anticrossing gap in Floquet system is also enlarged.The last panel shows the calculated conductance at different Fermi levels with laser fluence 0.23 mJ/cm2.These results indicate that the gap in Floquet system is topological nontrivial.
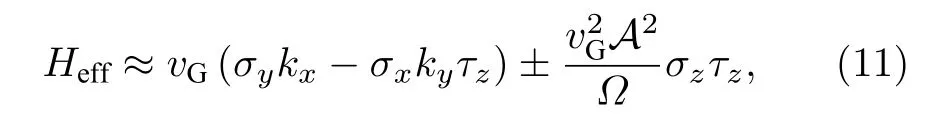
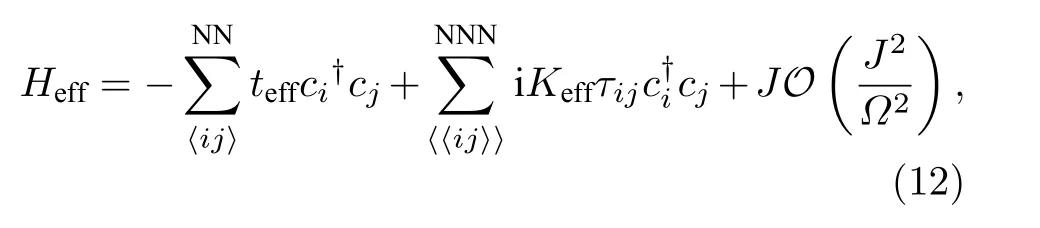
上述弗洛凯系统及其拓扑物态已经在若干实验中得到验证.2012年Fang等[61]提出在光子晶体体系使用动态调制其内部耦合大小的方式, 在棋盘状光子晶体中实现了等效磁场和不受缺陷干扰的边缘态.2013年, Rechtsman等[62]利用光子晶体沿轴传输特性等价于随时间演化的特点, 在静态系统中实现了等效的弗洛凯系统, 在实验上观察到了沿边界传输的边缘态, 如图3(c)所示.在石墨烯纳米带上施加圆偏光, 同样出现类似的边缘传输行为.Gu等[93]计算在施加圆偏光情形下不同宽度的石墨烯纳米带的电导, 随着纳米带的宽度逐渐增加, 展现出由边缘贡献的量子化电导平台.2019年,McIver等[94]利用泵浦-探测技术测量了激光照射石墨烯的反常霍尔电导.改变激光强度测量电导变化, 得到两者之间为接近线性关系, 如图3(d)所示.当逐渐增强光场强度, 石墨烯的弗洛凯-布洛赫能隙越来越大, 电导平台出现在与光场打开的拓扑能隙中.然而电导平台并没有符合理论预言的完全量子化, 这表明电导除了弗洛凯准粒子的能带贡献以外, 还有来自非平衡态下载流子占据分布带来的部分贡献.
4 弗洛凯系统中的外尔费米子与拓扑相变
1929年, Hermann[98]根据狄拉克方程给出一类新的无质量费米子, 随后这类粒子被称为外尔费米子.在固体物理中, 在外尔半金属费米面附近的低能激发表现出外尔费米子的行为, 在费米面附近三维倒空间中呈现线性色散关系的能带.贝利曲率等效于在倒空间中的赝磁场, 而倒空间中的外尔点处贝利曲率发散, 不同手性的外尔点对应贝利曲率的源和漏, 在费米面出现连接两个外尔点的费米弧, TaAs, WTe2等材料均被证实为外尔半金属[9,99,100].人们在诸如光子晶体等人造晶格中也发现了外尔半金属的拓扑能带结构[101,102].外尔半金属具有多样的奇特物性, 如手性异常[9,103]、量子霍尔电导信号[104]、非线性光电流[105]等, 与其外尔点的位置、手性及其拓扑物性相关, 因此如何利用外界光场等方式调控材料能带发生Lifshitz相变从而改变体系的拓扑性质, 进而改变体系的输运性质和拓扑光电响应是当前凝聚态物理的重要前沿.
与具有四重简并度的狄拉克点不同, 外尔点具有两重简并.实现狄拉克点到外尔点的相变需要破缺体系的中心反演对称性或时间反演对称性抑或同时破缺前两者.为了不显性地破缺体系的对称性, Hübener等[97]提出利用周期性光场手段实现调控三维狄拉克半金属材料的拓扑相变.Na3Bi是一种典型的狄拉克半金属材料[13], 倒空间Γ点附近的kz方向上存在两个三维狄拉克点, 如图4(a)和图4(b)所示.Collins等[44]将Na3Bi制备成单层和双层薄膜, 借助外部电场, 实现了室温的拓扑绝缘体至普通绝缘体的转变.在没有外场作用下, 无质量的狄拉克费米子的哈密顿量可以写为两个具有相反手性的外尔费米子的哈密顿量的直和.
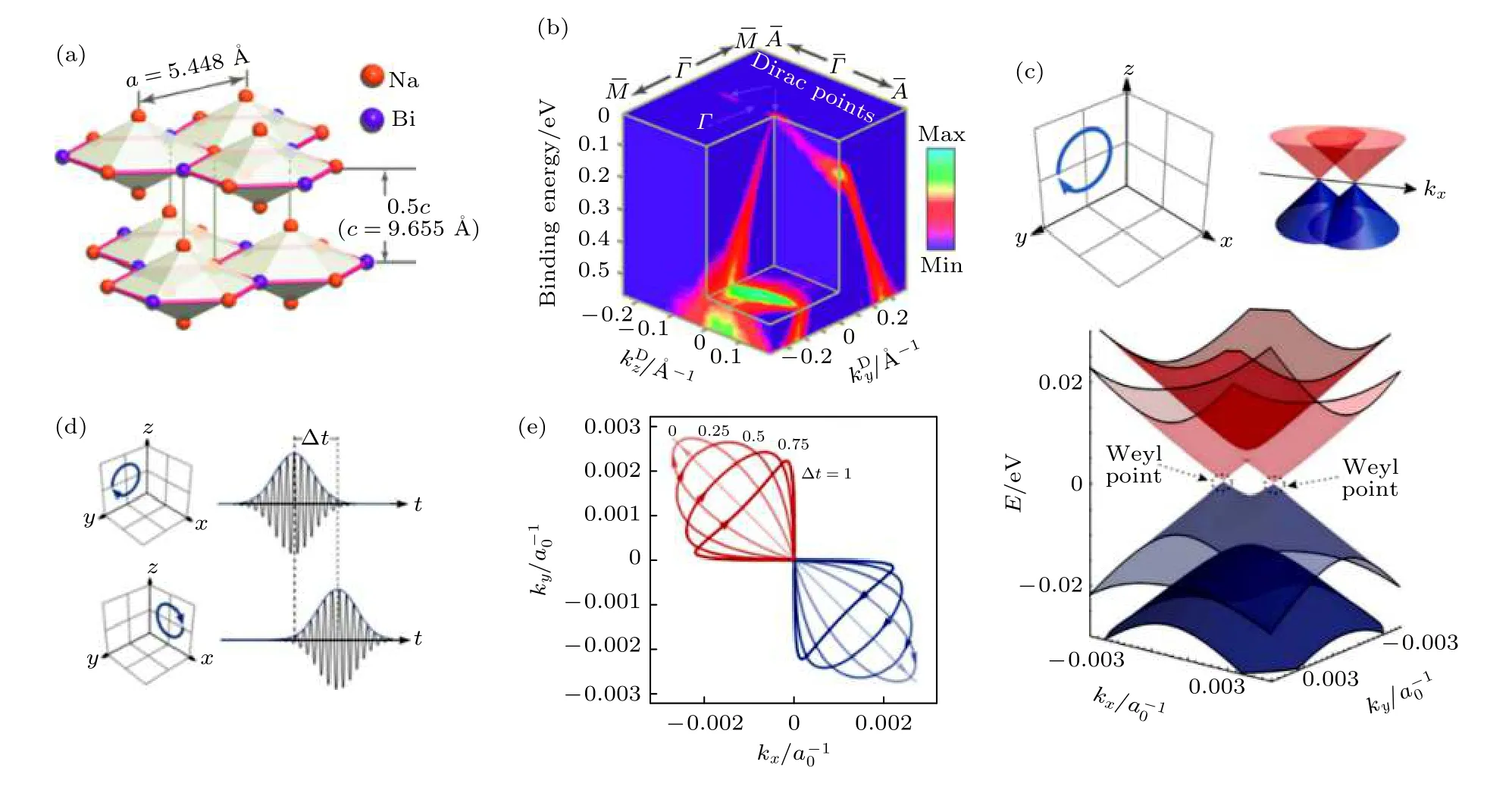
图4 光场驱动下三维狄拉克半金属Na3Bi的原子结构和电子结构 (a) Na3Bi原子结构示意图[13]; (b) 利用角分辨光电子能谱测量得到Na3Bi能带, 展现了其狄拉克点位置和线性能带色散关系[13]; (c) 沿着Na3Bi的x轴方向施加圆偏光, 三维狄拉克锥沿kx方向劈裂为两个手性相反的外尔锥[97]; (d) 沿着Na3Bi的x轴方向施加泵浦圆偏振光, 沿着y轴方向施加探测圆偏振光[97];(e) TDDFT得到的弗洛凯-外尔点在倒空间中移动轨迹[97]Fig.4.Light field driven electronic phase transition of three-dimensional Dirac semimetal Na3Bi: (a) atomic structures of Na3Bi[13];(b) band structures of Na3Bi near Dirac points measured by ARPES, The location of Dirac points and its linear dispersion are presented as well[13].(c) when the circularly polarized light is applied along to the x axis of Na3Bi, the Dirac cone will inherently split into two Weyl cones with opposite chiralities along kx direction[97]; (d) schematics of the circularly polarized pump and probe laser irradiated along the x axis and y axis of Na3Bi[97]; (e) varying delay time during the laser pulses leads to dancing Floquet-Weyl points calculated by TDDFT[97].

其中vF为费米速度,σ=(σx,σy,σz) 为泡利矩阵,k为相对于狄拉克点的动量.通过在x方向施加在y-z平面内振动的圆偏振光A(t)=A0(0,cos(Ωt),sin(Ωt)), 利用(13)式可以得到光场作用下无光子的过程和单光子虚过程修饰的有效哈密顿量为[97]

圆偏振光的引入使得不同手性的外尔有效哈密顿量在kx方向上发生了偏移, 且大小相等(均为方向相反, 如图4(c)所示.结合第一性原理弗洛凯-含时密度泛函理论(time-dependent density-functional theory, TDDFT)计算, 分别沿着Na3Bi的x轴方向和y轴方向施加泵浦和探测圆偏光, 两束光的时间差为 ∆t, 如图4(d)所示.弗洛凯调控的外尔点将在kx-ky平面内移动.随着∆t的变化, 外尔点在倒空间的移动轨迹如图4(e)所示.结合光场对晶格畸变的调节, 在Na3Bi中还可以实现金属相到拓扑绝缘体相的转变.
针对弗洛凯系统中外尔费米子的调控, Bucciantini等[106]则更进一步地讨论了在低频状态下圆偏光对狄拉克点的驱动情况.逐渐增大A/Ω的大小,不仅可以实现上述狄拉克锥的劈裂, 还可以使得系统由子空间n= 0和n= ± 1产生的外尔点接触并湮灭.
5 有质量二维体系中的光场修饰态
硅烯[108,109]是一种有原子褶皱的二维蜂窝状材料.与石墨烯类似, 具有狄拉克锥型能带色散关系, 高的载流子迁移率等优异特性.与单层石墨烯不同的是, 硅烯的原子褶皱打破了垂直硅烯平面方向的镜面对称性, 其AB子晶格沿z方向的垂直间距可由 2l刻画, 其中l= 0.23 Å.硅烯的本征自旋轨道耦合(spin orbit coupling, SOC) 强度为λso=3.9 meV, 远大于石墨烯, 原子褶皱则进一步加大了SOC能隙的大小, 因此硅烯也可被视作有质量的狄拉克材料.通过施加垂直硅烯平面的电场, 硅烯K点的能隙大小与电场呈现线性依赖关系[110,111],且2012年Ezawa[112]研究了硅烯在直流电场和交换电场下的拓扑态.当考虑直流电场响应时, 硅烯存在一个临界电场Ecr=λso/l= 17 meV/Å, 此时硅烯的能隙刚好被关闭; 继续增加电场, 硅烯的能隙重新打开, 实现从拓扑非平庸态到拓扑平庸态的相变, 在此相变过程中,K和K'能谷的能隙大小依旧相等.
而将前述交换电场替换为手性周期性光场[29]并保留电场自由度, 则空间和时间反演对称同时被打破,K和K'谷的能隙大小不相等, 有望在硅烯中获得谷极化的拓扑态.采用近似到一阶的弗洛凯有效哈密顿量处理圆偏光对硅烯电子结构的影响,硅烯的狄拉克质量项为
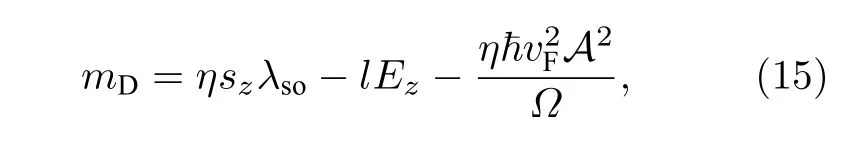
其中η=±1 分别对应于K和K'谷,sz=±1 对应于上下自旋, 产生的能隙为 2|mD|.不同能谷和自旋下的拓扑荷由此得到自旋陈数Ezawa[29]进一步研究了包含光诱导自旋极化情形的拓扑相图, 如图5(a)所示, 图中前缀P和S分别代表光诱导和自旋极化, 红色和蓝色的分割线代表谷极化的单自旋狄拉克锥过渡态, 如图5(b)所示.参照(15)式, 这些拓扑态的相变临界点对应于单自旋通道的单能谷能隙恰好关闭, 此时陈数和自旋陈数分别发生1和1/2的跃变, 从而将相图划分为多个拓扑荷不相同的绝缘区域.当直流电场大于临界电场时, 即满足Ez>Ecr时, 硅烯产生光诱导自旋极化的量子霍尔绝缘态, 其陈数和自旋陈数分别为1和1/2.这样的结果表明手性周期性光场可以扩展材料体系的拓扑同伦空间, 从而实现一些平衡态下无法实现的新奇物态.

图5 有质量二维体系的光场修饰态 (a)同时考虑电场和光场硅烯的有效哈密顿量对应的相图[29].横纵坐标分别对应电场强度 E z 和 A 2/Ω(A2 为光强, Ω 为光场频率).拓扑荷由 ( C,Cs) 描述, C 为陈数, Cs 为自旋陈数.(b) 硅烯中的单自旋狄拉克锥能带示意图[29].K' 能谷为能隙关闭的单自旋线性色散, K能谷则保持抛物线型能带色散.(c) WS2谷选择的光学斯塔克效应能级示意图[43].(d) WS2谷选择的布洛赫-西格特位移能级示意图.(e), (f) 不同能谷的手性弗洛凯拓扑态[107].控制失谐量Δ诱导能级反转并改变导带与弗洛凯边带的杂化, 由于排斥作用K能谷的能带交叉被禁止而K' 能谷发生能带交叉, 形成手性边界态Fig.5.Photon dressed states in two-dimensional systems with massive Dirac fermions: (a) Phase diagram of silicene by using effective Hamiltonian considering both electrical field and light field[29].(b) Sketch of silicene in the single Dirac cone state[29].The K valley exhibits a parabolic dispersion while the K' valley remains the linear dispersion.(c) Schematics of the valley-selective OSE in WS2[43].(d) Schematics of the Bloch-Siegert shift in WS2.(e), (f) Valley-specific Floquet topological phase in WS2[107].The band inversion and hybridization of Floquet sidebands is tuned by Δ and the chiral edge state is formed due to OSE.
作为一类典型的二维半导体材料, 过渡金属二硫化物(transition metal dichalcogenides, TMDs)如MoS2, WS2, MoSe2等具有优异的光学性质[113,114],其独特的能谷赝自旋自由度在谷电子学信息器件中有潜在应用[42].单层2H相TMDs六角蜂窝状的晶格结构在布里渊区边界拥有两个由时间反演对称性相关联的能谷K和K'[115], 在能谷处具有较大的直接带隙, 如单层MoS2能隙为1.89 eV[116].当被一束左旋σ−(或右旋σ+)的圆偏振光激发后,圆偏光打破了体系时间反演对称保护的简并能谷,K和K'能谷选择性地与σ−和σ+圆偏光耦合, 形成谷选择圆偏二色性, 从而产生谷极化, 本质上这是一种满足磁量子数守恒的手性选择定则[117].由于贝利曲率扮演着倒空间磁场的作用, 在面内电场驱动下, 具有相反符号的谷极化载流子将发生类似于洛伦兹力的偏转, 在横向方向形成反常的谷极化电流, 因而无中心反演的TMDs材料表现出新奇的谷电子学特性.由于强自旋轨道耦合和中心反演对称性破缺, TMDs材料的价带顶劈裂成两条自旋不简并的能带, 且在K和K'处自旋极化相反, 形成独特的自旋-能谷耦合效应[116].由于双层TMDs材料具有空间反演对称性, 能谷特性与层自由度进一步耦合, 形成更加独特的能谷-自旋-层的新奇光电特性[118].
光场辐照下TMDs的新奇特性来源于光学斯塔克效应(optical Stark effect, OSE), 由于该效应较弱, 只在少数的半导体量子点/量子阱中被观测到[119–121].这里将借助光场修饰后的弗洛凯态来理解光学斯塔克效应以及布洛赫-西格特位移[122].为简化讨论, 本文以半经典的两能级系统为例描述,弱场条件下, 外加电磁场视为对哈密顿量的微扰(此时半经典描述与二次量子化表述[123]的结果等价).若非相互作用体系的平衡态由哈密顿量H0描述, 本征态为|a〉和|b〉, 对应能级Ea 其中Mab=〈b|pˆ|a〉为极化矩阵元, 态间排斥产生的总能级位移为 如果电场由静态变为周期震荡, 假定ε(t)=ε0cos(2πνt),ν为频率, 满足非共振条件∆=Eb−Ea−hν>0,∆为激光的失谐量,h为普朗克常数.通过对一个时间周期求平均, 所得能级移动为 从光场修饰的准静态能级角度出发, 周期光场激发使得在平衡态|a〉和|b〉的基础上产生光场修饰的弗洛凯态, 近似到一阶, 这四个虚光子态分别为|a±hν〉和|b±hν〉.若只考虑其中的两个|a+hν〉和|b−hν〉, 接近共振条件下, 体系主要的耦合来源于|a+hν〉和|b〉以 及|b−hν〉和|a〉两对态之间的杂化, 参考(16式)可知在|a〉和|b〉间贡献了额外的光学斯塔克位移项.以K谷的态为例, 光场辐照后的弗洛凯态为由于与导带的磁量子数一致, 故发生耦合杂化, 能级发生位移为 ∆E, 而K'谷则不发生光学斯塔克效应.如图5(c)所示, 使用σ−泵浦光激发后, 探测到的能级位移仅发生在K能谷.与之相反, 如图5(d)所示, 使用反旋转泵浦光源, 探测到WS2的能级位移仅仅发生在K'能谷.|a−hν〉和|b〉以及|b+hν〉和|a〉两对态的杂化产生布洛赫-西格特位移, 只不过在接近共振时可以忽略不计.谷选择的光学斯塔克效应和布洛赫-西格特效应对于理解辐照下TMDs材料的新奇效应具有重要意义. 基于上述原理, Sie等[107]借助泵浦-探测瞬态吸收光谱技术研究了单层WS2谷选择的OSE.考虑到WS2最低的激子态为2.0 eV, 所采用的泵浦脉冲能量略低于激子能量(1.68—1.88 eV).实验中测量了吸收光谱前后的变化量 ∆α, 时间分辨的 ∆α轨迹说明OSE仅在泵浦和探测光无延迟( ∆t=0 )时发生, 谷间极化的吸收谱则说明WS2中的OSE确实具有谷选择性.若假定吸收谱α(ω)关于吸收峰呈正态分布, 借助光谱权重转移公式可确定能级位移 ∆E为 其中A为样品最大的吸光度, 积分范围为2.00<ω<2.18 eV.通过 ∆E与光强及失谐量的关系论定该位移项由OSE贡献且其最高能量尺度为18 meV.考虑到控制激光的失谐量可以实现两能级系统能隙的关闭, 以及虚光子弗洛凯边带的能级排斥, 作者提出当∆<0 时有机会在特定能谷实现周期场驱动的手性边缘态, 如图5(e)和图5(f)所示.在后续的工作中, Sie等[43]使用远离共振条件的红外泵浦脉冲(0.59—0.98 eV), 进一步在WS2中观测到了特定能谷的布洛赫-西格特位移, 最大可以达到10 meV.同时作者在另一个能谷中也观测到了光学斯塔克位移.基于弗洛凯准静态的图像我们可以十分直观地理解周期光场对WS2平衡态谷电子学的影响, 然而当体系几乎共振时, 弗洛凯光修饰态的模型将不再适用.Cunningham等[124]指出这时需要考虑包含库仑多体相互作用的激子模型. 第Ⅴ主族元素晶体材料黑磷是近年来较为热门的一类层状材料.本征的体相黑磷是拓扑平庸的半导体, 其能隙约为0.3 eV, 具有各向异性的载流子特性[126,127]和优异的光电特性[128].表面掺杂的黑磷中可以出现时空反演对称性保护的第二类狄拉克费米子[129], 在压应力的条件下(不考虑自旋轨道耦合)黑磷则可以转变为拓扑节线半金属[130], 节线环平面平行于层状堆垛方向, 因此压应力下黑磷的拓扑节线半金属表现了极强的各向异性. 鉴于平衡态下的黑磷具有极强的各项异性, 其非平衡态下的拓扑态同样值得关注.本文作者之一与合作者[69]通过基于第一性原理计算的瓦尼尔哈密顿量首先研究了压应变下黑磷在圆偏光下的非平衡态电子结构.当沿扶手椅方向(图6(a)中x方向)施加2%的压缩应力后, 黑磷的能隙会被关闭,为方便讨论, 可以选取压应变为3.72%的黑磷, 此时在布里渊区(100)投影面(图6(b))出现以Z点为中心的节线环.考虑入射的圆偏光为 图6 压缩应变黑磷中的弗洛凯狄拉克费米子和拓扑相变 (a) 沿x方向压缩3.72%的黑磷原子结构.(b) 平衡态压缩黑磷的体相布里渊区以及(100)投影面[69].拓扑节点环出现在Γ-Z-W平面.(c) 光子能量0.5 eV下的黑磷的弗洛凯态的相图[69].变量为激光振幅 A 0 在y-z平面内的入射角 θ , 如图(a)所示.(d)—(f) 光子能量0.5 eV下由激光驱动的弗洛凯狄拉克费米子发生拓扑相变[69](d) A 0=50V/c ; (e) A 0=263V/c ; (f) A 0=300V/c.c 为光速, 施加的圆偏光为 A (t)=A0(cos(ωt),sin(ωt),0).(g) 通过在节点环能带结构中施加激光照射, 可以实现高陈数外尔点[125]Fig.6.Floquet-Dirac fermions and topological phase transition in compressed black phosphorus.(a) Atomic structure with 3.72%compressive strain along x direction.(b) Bulk first Brillouin zone and projected (100) surface.Here, the topological nodal ring appears in the Γ-Z-W plane.(c) Topological phase transition driven by laser with varying laser amplitude and incident angle of y-z plane θ under a fixed photon energy 0.5 eV[69].(d)–(f) Floquet-Dirac band structure under different laser parameter[69]:(d) A 0=50V/c ; (e) A 0=263V/c ; (f) A 0=300V/c.c is the speed of light.(g) Construction of high Chern number Weyl points in nodal ring under incident light[125]. 结果表明在较宽的激光光谱范围内压缩应力黑磷都将存在多种弗洛凯态, 弗洛凯-狄拉克锥与光场参数的依赖关系如图6(c)所示. 当压缩黑磷被沿z方向传播的周期圆偏光驱动时, 首先出现的是节线环转变为一对第一类弗洛凯-狄拉克点, 如图6(d)所示, 此时狄拉克点的连线方向出现在节点环的短轴Γ-Z方向, 且与入射光场方向平行; 而与入射光场垂直方向上节线环的其他动量点均打开能隙.若只考虑价带顶, 平衡态能带(n=0 )和弗洛凯边带(n=−1 )会产生OSE带间排斥, 且带间排斥在n=0 和n=−1 两条能带原先有交点时正比于激光的振幅A0[131].随着激光振幅的增强, 不仅弗洛凯-狄拉克锥的间距沿ΓZ方向逐渐变小, 而且非平衡态价带顶在该点附近的倾斜程度随着OSE排斥而增大, 逐渐转变为第三类[132]和第二类[9]弗洛凯狄拉克锥(分别如图6(e)和图6(f)所示, 这里只给出了节线环上其中一个弗洛凯-狄拉克锥附近的能带). 光场操控不仅可以得到弗洛凯拓扑绝缘体相,且其所对应的拓扑表面态也与圆偏光的手性相锁定, 而且有希望实现光场调控下的非平衡态的手性电子输运.这些结果不但加深了人们对弗洛凯驱动拓扑相变的理解, 也为非平衡态黑磷在光电子学等领域的应用提供了理论依据. 对于一般的节点环能带结构的弗洛凯工程来说, Yan和Wang[125]以及Ezawa[133]讨论了节点环能带结构中加圆偏光后, 使得节点线能带变为成对的弗洛凯-外尔点, 而且圆偏光的手性决定了产生的弗洛凯-外尔点的手性.而在具有共同节点的节点环能带结构中, 利用光场调控外尔点的位置,则可以产生具有高陈数的外尔点, 如图6(g)所示. 在固体材料中, 周期性的晶格振动通过与电子的瞬时运动耦合会使材料进入非平衡电子态, 相干声子通过与电子的耦合来修饰原先的电子态, 使其形成准粒子, 产生一系列复制的弗洛凯边带并相互杂化.相干声子可以通过光学激发的方式获得, 由于声子是有质量的玻色子且其振动周期的时间尺度远大于光子, 电子对晶格振动的响应几乎瞬时,导致相干声子驱动下的非平衡态性质会区别于前文的周期光场修饰态. 由于电子的运动速度远大于离子, 通常电子-声子相互作用可以近似成冷冻声子, 然而近年来人们发现越来越多背离绝热近似的情况, 如石墨烯等[31].为验证光场驱动下相干声子对量子材料电子结构的动态修饰效应而使得冷冻声子近似失效,Hübener等[48]通过基于TDDFT的埃伦菲斯特分子动力学研究了石墨烯在光场产生的E2g相干声子驱动下的弗洛凯能带, 并与计算得到的时间-角度分辨光电子能谱相比较.不同于周期平均的冷冻声子近似下的结果, 相干声子驱动确实会出现大量复制的弗洛凯边带.当观测的时间超过声子的振动周期时间尺度时, Tr-ARPES与弗洛凯能带符合得很好.与周期光场驱动的石墨烯一致[37], 手性相干声子将在石墨烯的K点引入质量从而打开拓扑能隙(图7(a)和图7(b)), 而线性相干声子则保持能谷附近的能带交叉点. 由于光场驱动下的相干声子可以修饰电子结构调控能隙的闭合, 因此该方法可以诱导量子材料发生拓扑相变.ZrTe5的单层结构是大能隙的拓扑绝缘体[135], 块状结构则随着层间距变化呈现出强拓扑绝缘体到狄拉克半金属态再到弱拓扑绝缘体的转变.虽然温度[136]以及应力[47]可产生类似效应并诱导相应的拓扑相变, 但都是平衡态下的物性调控.最近, Vaswani等[134]提出通过超快激光产生相干声子, 可以实现对非平衡态的晶格及其对称性的操控.他们发现利用短周期太赫兹强脉冲激光可以激发ZrTe5中特定A1g光学支声子模(图7(c)),从而实现光场调控量子材料的拓扑相变.这种非热驱动的模式选择激发借助拉曼相干声子注入的方式实现ZrTe5层间原子的位移, 在临界位移时产生狄拉克点和拓扑Lifshitz相变. 前文讨论了二维材料TMDs中的光场修饰态.改为声子驱动时, 自旋轨道耦合效应将晶格振动与自旋相互耦合, 形成新的自旋动力学.Shin等[40]通过TDDFT结合弗洛凯理论探讨了MoS2中声子修饰的自旋-能谷态, 发现在MoS2的K能谷导带底附近(图7(d)), 所有的振动模式中只有同时打破镜面和三重旋转对称性的E''振动模式可以与自旋自由度运动相耦合, 从而动态改变自旋的方向(图7(e)).从简化哈密顿量角度分析,E''声子可以产生沿该方向的等效周期磁场.若考虑由两个相位相差 π /2 的E''线性声子构成的右旋声子, 在该声子的驱动下对应的自旋-弗洛凯态如图7(f)所示, 每一个声子量子产生 0.024µB的净面外磁矩. 图7 光场驱动下相干声子驱动的弗洛凯态 (a) 由石墨烯E2g振动模中简并的横向和纵向声子模(相位差 π /2 )产生的手性圆偏声子[48]; (b) 手性相干声子驱动下计算得到的石墨烯Tr-ARPES以及TDDFT结果与弗洛凯能带相符合[48]; (c) ZrTe5的原子结构和层间振动模式A1g示意图[134]; (d) 平衡态下单层MoS2的能带结构, 蓝框标注的是K能谷附近的导带底[40]; (e) MoS2自旋倾向角与上下自旋能隙 ∆ ε 关于沿声子振动模E'' 方向位移Δds的关系图, 插图为E'' 的振动模式[40]; (f) MoS2在K和K' 能谷由右旋声子定义的两个自旋-弗洛凯本征态[40]Fig.7.Floquet states induced by coherent phonons driven by periodic light field: (a) Circularly chiral phonons generated from the degenerate LO and TO phonons (with phase difference π/2) of E2g vibration mode of graphene[48]; (b) calculated Tr-ARPES of phonon-driven graphene fits well with TDDFT simulations[48]; (c) atomic structures and interlayer vibration mode A1g of ZrTe5[134];(d) band structure of monolayer MoS2 under equilibrium[40], the blue box marks the lowest conduction band near K valley; (e) relationship between the spin inclination angle and the up/down spin splitting Δε with respect to the displacement Δds along the phonon mode E'', the inset shows the E'' vibrational mode[40]; (f) spin-Floquet eigenstates of MoS2 at K and K' valleys induced by the right circularly polarized phonon[40]. 在经典物理中周期性驱动的体系能够实现平衡态下无法实现的非平衡现象, 如稳定倒立的卡皮察摆, 大密度液体悬浮于小密度液体之上[137]等.针对周期性驱动的量子系统, 人们从弗洛凯定理出发, 通过将其映射至静态弗洛凯哈密顿量, 用准静态方法描述系统的非平衡态动力学行为.由于非平衡态弗洛凯系统引入了时间自由度, 弗洛凯系统本征态扩展成的广义希尔伯特空间, 因而时间-空间对称性的联合操作为体系提供了更加丰富的拓扑分类[54].本文介绍了周期性外场驱动的弗洛凯系统的奇特性质, 加深了人们对周期性外场驱动量子系统的认识, 为帮助人们理解凝聚态系统的基本性质提供了重要参考.其次, 弗洛凯工程也为理解凝聚态系统行为提供新视角.人们发现量子材料的非线性光学过程产生的位移电流具有拓扑内涵, 利用弗洛凯工程能够调控该奇特物性[89].在多体系统中, 如时间晶体与多体系统局域化密切相关, 弗洛凯工程在调控诸如量子液体, 电荷密度波等系统中也有工作报道[138,139]. 回顾前述内容, 利用光场调节弗洛凯系统中电子能带结构或拓扑性质, 或者是光场激发相干声子的晶格振动诱导体系相变, 弗洛凯工程拓宽了材料属性的边界.然而量子材料的超快相变等动力学行为, 仍有待进一步探索.在物性调控上, 光场诱导瞬态超导内部机制研究, 亦或光场诱导磁结构变化, 外界光场驱动弗洛凯系统中电子-声子相互作用同样扩展了材料可调状态的边界. 关于弗洛凯系统以及弗洛凯工程的研究刚刚开始, 相关理论和应用需要进一步的深入研究, 比如弗洛凯系统中的非平衡输运性质的调控, 量子材料内元激发如何修饰弗洛凯态及其对物性的影响,弗洛凯工程如何调控多体系统或者无序系统等问题.弗洛凯系统和弗洛凯工程的研究将会进一步推动凝聚态物理的发展.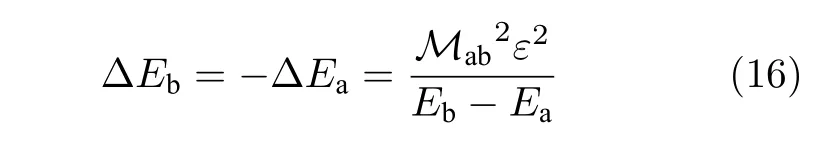
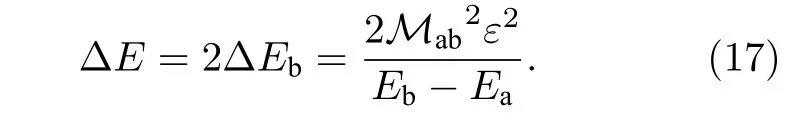


6 节点环能带中的弗洛凯狄拉克费米子

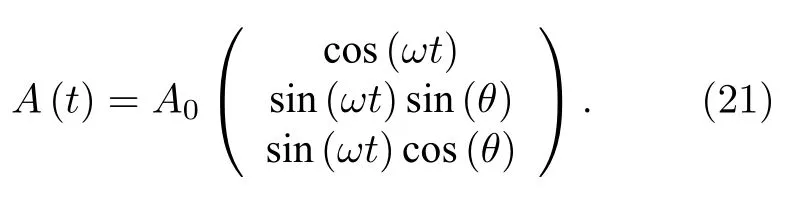
7 相干声子驱动的弗洛凯修饰态

8 结论与展望

