智能控制在罩式炉系统优化策略研究

金风涛

（甘肃钢铁职业技术学院，甘肃 嘉峪关 735100）

1 神经网络

复杂神经网络体系基于不同框架、模块以及运行模式下，对目标进行智能化运算的过程，其特定是智能化程度高、选择适用性高，在各大工业体系均具有广泛的应用。本文基于神经网络来优化预测函数，以希在智能化预测模型下实现对系统过程的智能化控制和调控。

图1 预测函数控制原理图

在预测函数模型中，MAC、DMC、GPC均具有良好的发展前景，但在罩式炉温度控制体系中，由于动态阈值区域较大，非线性峰值浮动不定，造成在温度控制中无法实时对参量控制，罩式炉环境参考无法实现精确控制，神经网络和预测函数模型的应运而生，通过基于控制模型构建环境变量模型，实现温度控制的精准控制，此外并入反馈模型还可实现参量的动态控制，实现模型的全域控制。

2 温度控制方式

PID（Proportion Integration Differentiation）作为一种前沿的调控方式，在各行各业均具有发展前景，目前主流市场上的主要有P.PI.PD以及PID，控制方式和模型具体如图2所示。

图2 PID控制系统的结构图

由图2可以看出，控制回路主要包括2大部分，其一是控制目标，其二是控制模型。通过控制系统的输入、输出参量来实现过程的反馈调节。

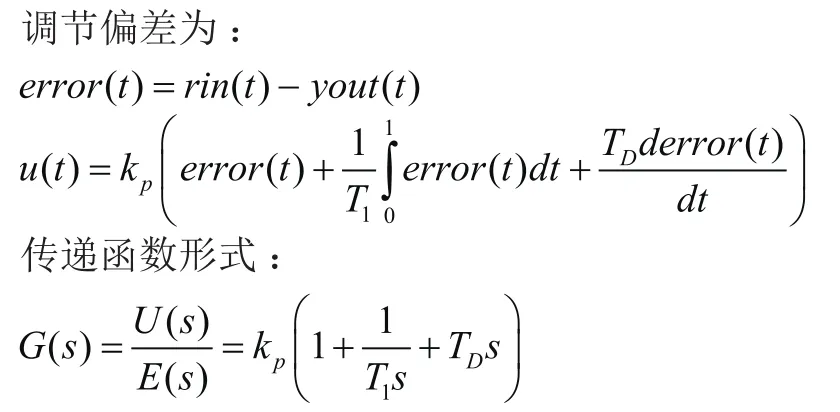
式中，KP为比例系数；T1为积分时间常数；TD为微分时间常数。

受传统的PID控制算法的影响，参量模型会随着环境变量发生改变，无法实现对过程控制的全域控制和反馈干扰，为提高系统的自适应性，提高系统在非线性环境下系统的调节精度和反馈波长。

本文基于罩式炉燃烧体系中温度参数调控模型，由于受参量影响较大，环境干扰因素较多，模拟参量、动态时域波动较大，为提高系统适用性、反馈精度和控制参量的时效性，现有控制体系无法实现对模拟参量的实时干预和环境变量模型的构建，基于神经网络体系构建预测函数，实现时域阈值、环境变量的实时干预控制。

3 预测模型构建

系统预测函数模型的建立是系统调控中必不可少的一个环节，因此建立不同的模型会有不同的预测性能。因此可以通过现有的数据信息来进一步预测系统预期数据的输出。而此时的预测模型在系统的框架上毫无任何约束，仅仅惟一的不同就在于使用途径上的不同，因此借助此功能赋予的模型特性就可以极大的增大系统评估的深度和宽度，这是以往简单数学模型所不及之处。

预测函数控制预测模型包括：

ym（k）的输出自由项；yL（k）零输入响应和强迫项yF（k）零状态响应组成，具体如下式所示。

3.1 反馈矫正

调节体系的响应修正，主要借助预测输出和实际输出形成一个误差校正值，其主要的原因是，在实际的应用中往往存在一些不能调控的参数和因子以及需要再次输入的参数值，造成实际输出之间会存在一个误差校正值；为了使得此校正值处于系统可接受之内，因此系统需要对其进行适当的评估。

式中，e（k+i）为过程与预测模型的预测误差，其为k时的误差与修正误差组成。

3.2 滚动优化

滚动优化是为了实现在优化时域H系统的输出和标准轨迹的平方和最小即式3-6、式3-7所示。

式中，nH拟合点数；（nn＞nB）；yP（k+i）是过程输出预测；ym（k+i）是k+i时刻模型输出；e（k+i）e为将来误差。

4 预测函数控制算法

5 预测函数控制结构

预测函数调控框架大体包括以下几个部分。其中预测函数中最主要的部分是基函数的选择、特定模型的规划以及相关控制器的部署和误差的校正和优化等，而本文主要是在锅炉燃烧系统的基础下建立的温度调控系统，其控制的结构形式如下图所示。

如上图3所示串级框架，W2（s）与W1（s）由于具有不同的属性而分别加以研究和讨论，将其划分为导前区和惰性区。系统主要的输入参数为减温阀门的调控量u，输出参数为此时系统的燃烧温度，为了使得预测效果达到最佳，需将图中虚线中的传递路线划为一个整个加以考虑。

图3 燃烧温度预测函数控制结构图

6 结束语

动态时域优化的评估函数的调节系统的稳定性最高，响应的时间及时，超调量的幅度也大大的降低。主要的原因是，系统自身就具有一定的误差校正功能，对应的调控装置能预先对产生误差进行修正，使系统更加稳定和可靠。此外此调控体系在于给定误差修正方法还具有一定的发展潜力。