识图、画图、读图狂练

一、单项选择题

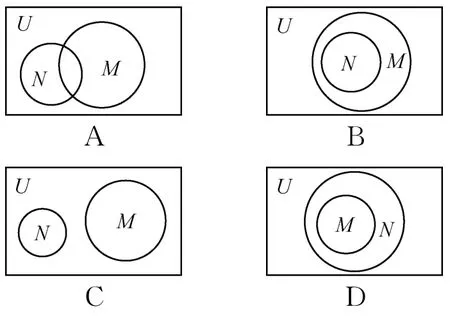
1.已知全集U＝R,则正确表示集合M＝{x|x2＋x＝0} 和N＝关系的韦恩(Venn)图是( )

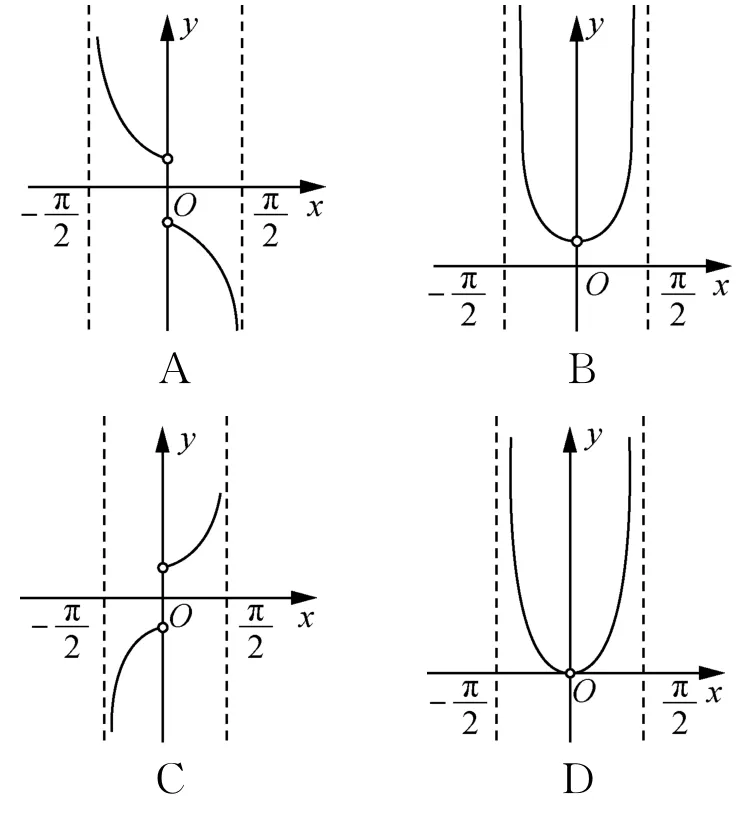
3.在数学的研究性学习中,常利用函数的图象研究函数的性质,也利用函数的解析式研究函数的性质,下列函数的解析式(其中e＝2.71828…为自然对数的底数)与所给图象最契合的是( )

(第3题)

A.y＝B.y＝

C.y＝D.y＝

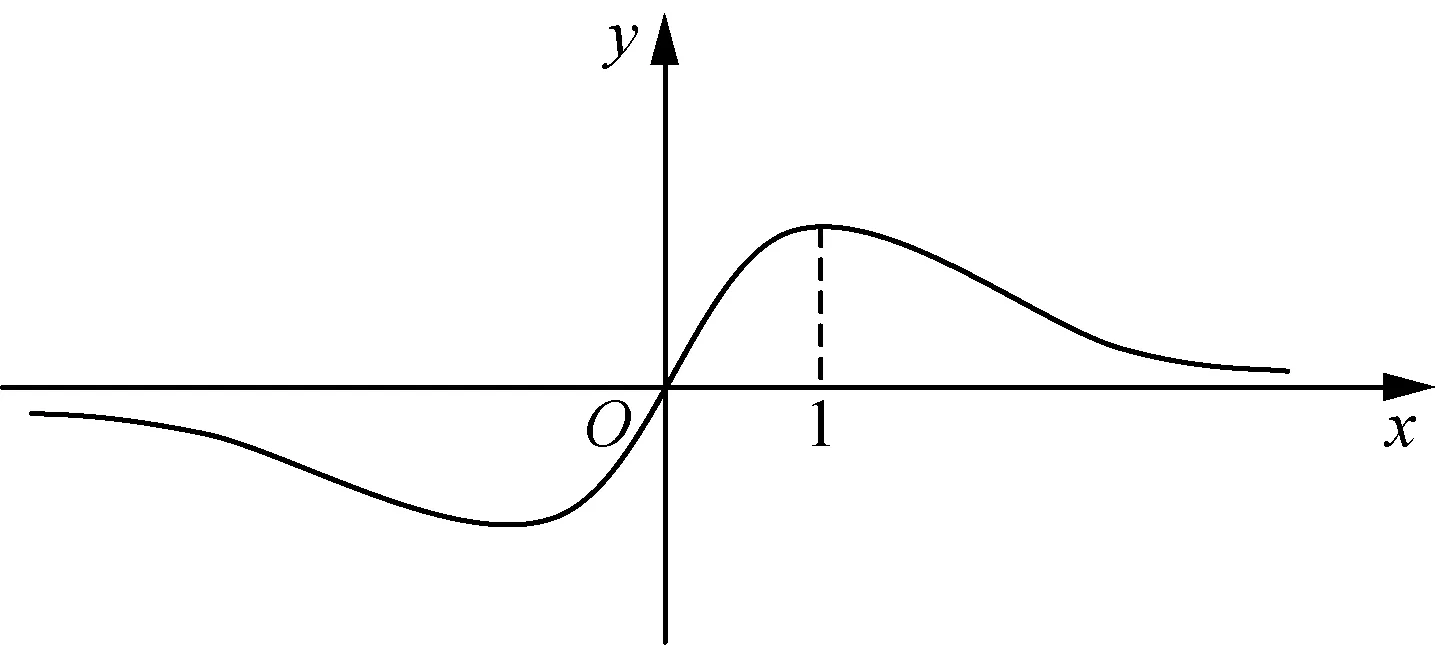
4.函数f(x)＝的大致图象如图所示,则下列结论正确的是( )

(第4题)

A.a＞0,b＞0,c＞0

B.a＜0,b＞0,c＜0

C.a＜0,b＜0,c＞0

D.a＞0,b＞0,c＜0

5.函数y＝(2x-2-x)sinx在[-π,π]的图象大致为( )

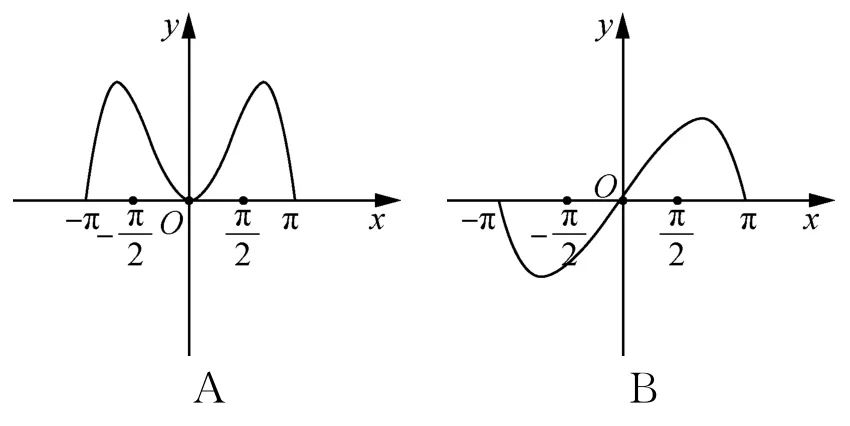
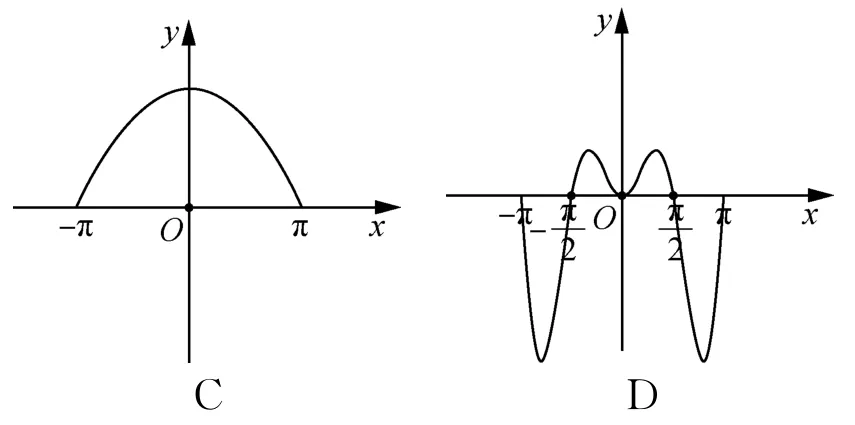
6.2019年诺贝尔生理学或医学奖获得者威廉·凯林在研究肾癌的VEGF抑制剂的过程中使用的输液瓶可以视为两个圆柱的组合体,示意图如图所示.开始输液时,滴管内匀速滴下液体(滴管内液体忽略不计),设输液开始后x分钟,瓶内液面与进气管的距离为hcm,已知当x＝0时,h＝13.如果瓶内的药液恰好156分钟滴完,则函数h＝f(x)的图象为( )

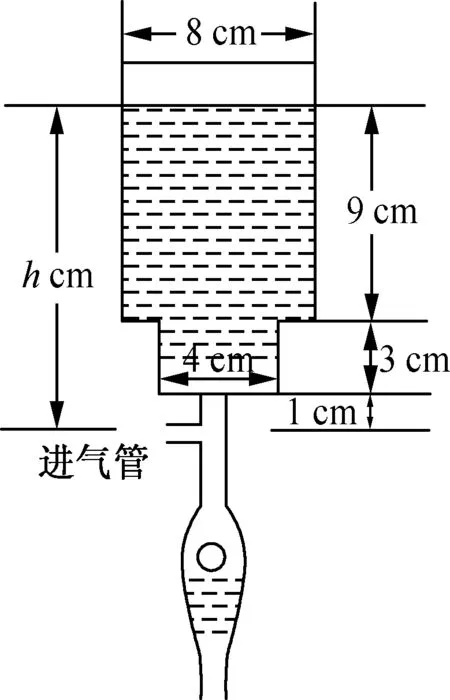
(第6题)

7.双纽线像数字“8”,不仅体现了数学的对称、和谐、简洁、统一的美,同时也具有特殊的有价值的艺术美,是形成其他一些常见的漂亮图案的基石,也是许多设计者设计作品的主要几何元素.曲线C:(x2＋y2)2＝4(x2-y2)是双纽线,则下列结论正确的是( )

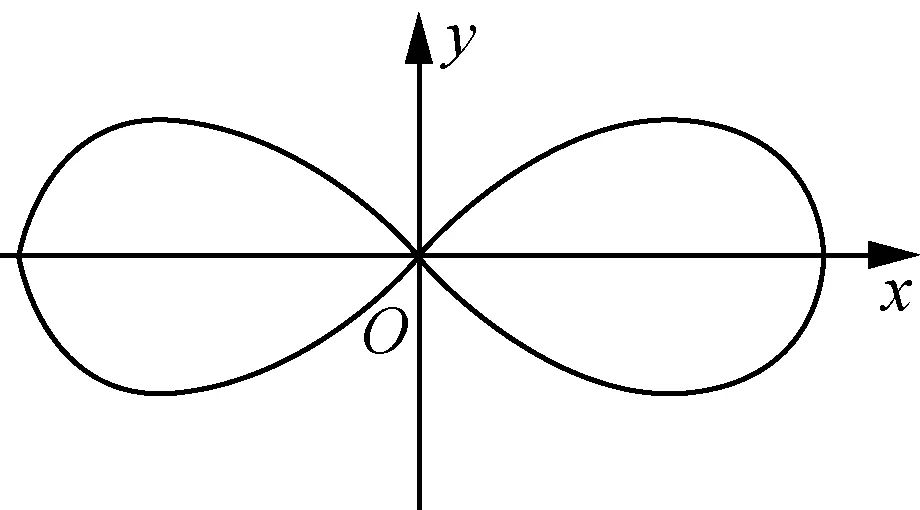
(第7题)

A.曲线C经过5个整点(横、纵坐标均为整数的点)

B.曲线C上任意一点到坐标原点O的距离都不超过

C.曲线C关于直线y＝x对称

D.若直线y＝kx与曲线C只有一个交点,则实数k的取值范围为(-∞,-1]∪[1,＋∞)

8.已知偶函数f(x)的定义域为R,对∀x∊R,f(x＋2)＝f(x)＋f(1),且当x∊[2,3] 时,f(x)＝-2(x-3)2,若函数F(x)＝-f(x)(a＞0,a≠1)在R上恰有6个零点,则实数a的取值范围是( )

9.(多选题)如图,矩形ABCD中,已知AB＝2,BC＝4,E为AD的中点.将△ABE沿着BE向上翻折至△A′BE,记锐二面角A′-BE-C的平面角为α,A′B与平面BCDE所成的角为β,则下列结论可能成立的是( )

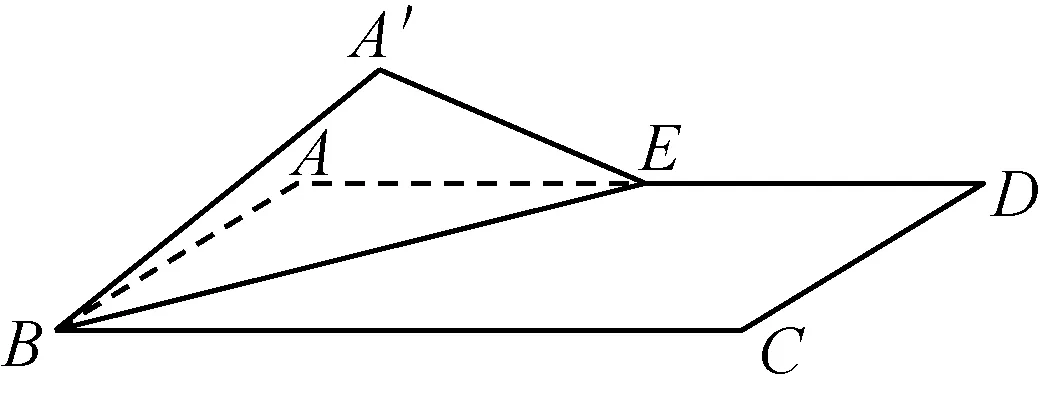
(第9题)

A.sinα＝B.

C.α＜2βD.α-β＞

10.(多选题)在三棱锥S-ABC中,△SAC,△SBC均是以SC为斜边的等腰直角三角形,SA＝,AB＝a,则下列说法正确的是( )

A.SC⊥AB

B.a∊(0,2)

C.该三棱锥的外接球的表面积为12π

D.当a＝2时,过点B且与平面CAB和平面SAB所成角都为15°的直线共有4条

二、填空题

11.若函数f(x)＝Acos(ωx＋φ)的部分图象如图所示,则φ＝________＝________.

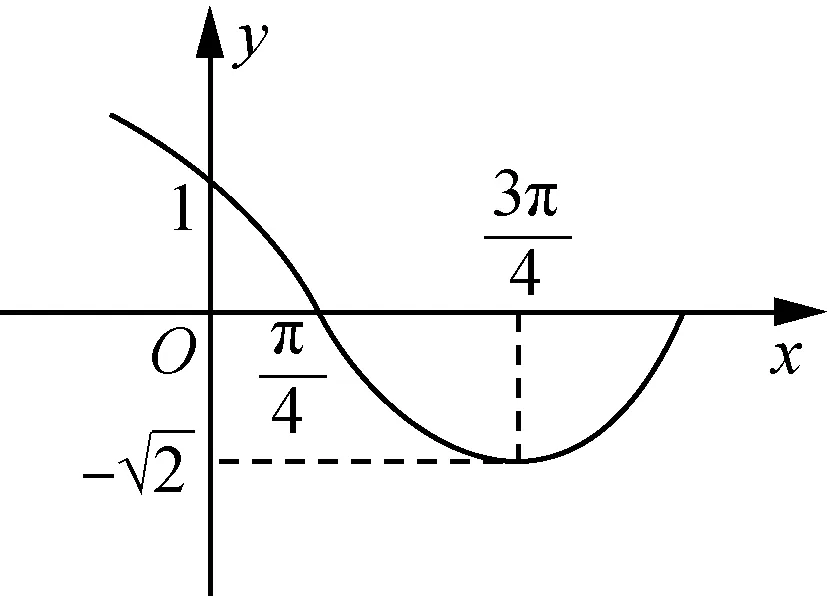
(第11题)

12.已知正方体ABCD-A1B1C1D1的棱长为1,以顶点A为球心,为半径作一个球,则球面与正方体的表面相交所得的曲线的长等于________.

三、解答题

13.如图,在△ABC中,B＝,D为边BC上的点,E为AD上的点,且AE＝8,

(1)求CE的长；

(2)若CD＝5,求cos∠DAB的值.

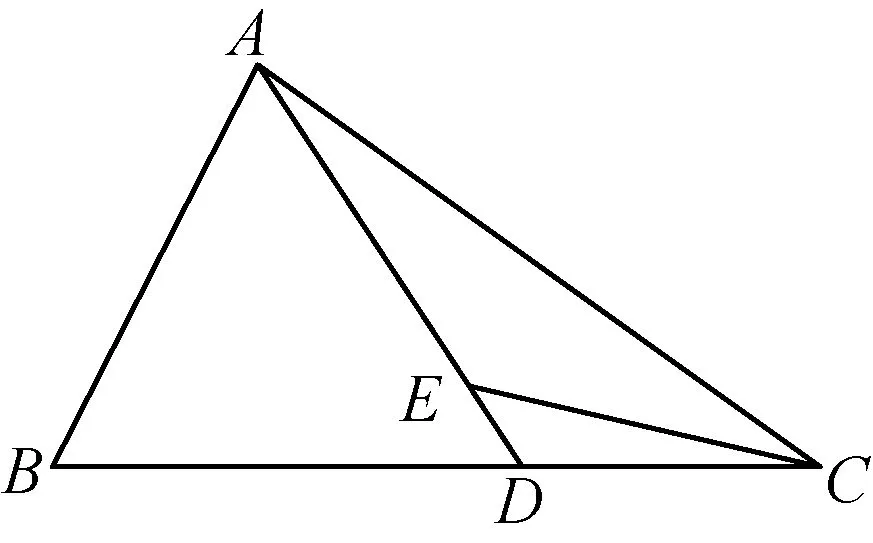
(第13题)

14.现有两个全等的等腰直角三角板,直角边长为2,将它们的一直角边重合,若将其中一个三角板沿直角边折起形成三棱锥A-BCD.如图所示,其中∠ABD＝60°,点E,F,G分别是AC,BC,AB的中点.

(1)求证:EF⊥平面CDG；

(2)求二面角F-AE-D的余弦值.

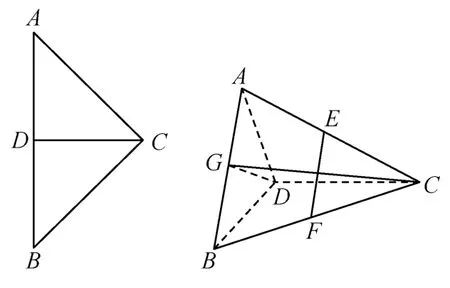
(第7题)

15.如图,在正三棱柱ABC-A1B1C1中,AB＝,A1A＝2,D,E,F分别为线段AC,A1A,C1B的中点.

(1)证明:EF∥平面ABC；

(2)求直线C1B与平面BDE所成角的正弦值.

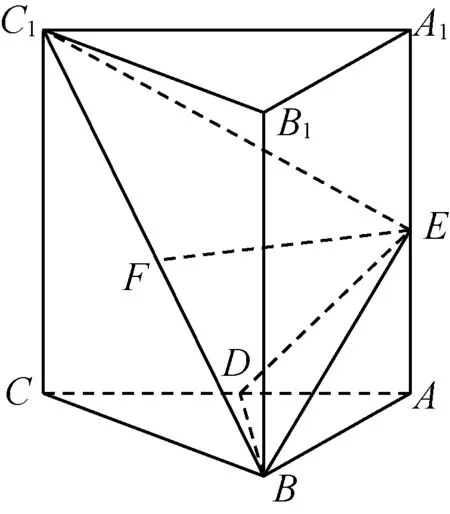
(第15题)

16.某市为了了解本市初中生周末运动时间,随机调查了3000名学生,统计了他们的周末运动时间,制成如图所示的频率分布直方图.

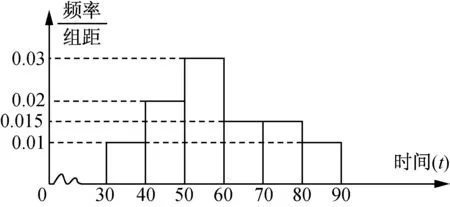
(第16题)

(1)按照分层抽样,从[40,50)和[80,90)中随机抽取了9名学生.现从已抽取的9名学生中随机推荐3名学生参加体能测试.记推荐的3名学生来自[40,50)的人数为X,求X的分布列和数学期望；

(2)由频率分布直方图可认为:周末运动时间t服从正态分布N(μ,σ2),其中,μ为周末运动时间的平均数,σ近似为样本的标准差s,并已求得s≈14.6.可以用该样本的频率估计总体的概率,现从本市所有初中生中随机抽取12名学生,记周末运动时间在(43.9,87.7]之外的人数为Y,求P(Y＝3)(精确到0.001).

参考数据1:当t～N(μ,σ2)时,p(μ-σ＜t≤μ＋σ)＝0.6826,P(μ-2σ＜t≤μ＋2σ)＝0.9544,P(μ-3σ＜t≤3σ)＝0.9974.

参考数据2:0.81859＝0.1649,0.18153＝0.0060.