基于自监督学习的温室移动机器人位姿跟踪

周云成，许童羽，邓寒冰，苗 腾，吴 琼

（沈阳农业大学信息与电气工程学院，沈阳 110866）

0 引言

在无导轨或辅助标志物引导的非结构化温室环境下，移动机器人需要通过自身传感系统探查工作场景结构，据此完成导航、定位和避障等功能，即机器人通常要具备即时定位与地图构建（Simultaneous Localization and Mapping, SLAM）系统，而位置及姿态（位姿）跟踪是其中的一个关键环节[1]。

传统温室移动机器人通过跟踪导轨[2]或辅助标志物实现导航定位。袁挺等[3]用铺设在硬化水泥路面中央的红色线作为导航标志物。高国琴等[4]以图像色调分量为特征，用番茄垄间路径与两侧的差异，通过阈值分割、边缘提取和Hough变换获取导航路径。居锦等[5]提出一种基于侧向光电圆弧阵列的下沉路沿或凸起路沿检测方法，实现道路沿边导航。这些方法可实现机器人的移动导引，但对温室建设结构及作物种植模式也提出了较高要求。日光温室构型和种植作物变化多样，如果机器人缺少对环境结构的获取和理解过程，也无相应的位姿跟踪与定位技术，则难以实现自主作业。为此，国内外学者在该方向上开展了相关研究。史兵等[6]利用无线传感器网络采集对机器人通过性有影响的环境温湿度，构建动态更新的环境信息栅格地图，实现机器人导航。该研究需要手动输入温室结构及障碍物位置信息，自适应能力有限。Masuzawa等[7]用Kinect v2相机作为视觉传感器，开发了一个园艺收获支持机器人原型，利用从一系列连续帧中提取的彩色图像特征点及对应深度来估计机器人运动及温室三维结构。Kinect易受日光干扰，且深度检测范围小。侯加林等[8]用双激光雷达和cartographer算法实现温室二维栅格地图实时构建和机器人即时定位。激光雷达可直接获取三维场景结构，精度高，但价格昂贵。彩色相机成本低，且图像可用于多种视觉任务，因此视觉SLAM（visual SLAM, vSLAM）[9-10]技术在机器人领域受到越来越多的关注。作为vSLAM的关键环节，深度和位姿估计等前端处理的精度将直接影响其性能。传统位姿估计[11]依赖人工设计的低级图像特征，其在常规环境下可取得理想结果，但当出现非刚体、遮挡、无纹理区域时，该类方法往往会失效[12]。得益于卷积神经网络（Convolution Neural Network, CNN）提取的高级图像特征[13]，基于深度学习的位姿估计方法取得了一定的研究进展[14-19]。Zhou等[14]提出一种深度和位姿变换估计模型，其利用不同视角下的图像重构误差作为监督信号来实现无监督学习，但由于训练过程中仅采用单目视频序列，该模型只能估计相机的相对位置变化。Zhan等[15]针对该问题，提出可用双目视频序列进行训练的自监督学习模型，基于双目基线约束，该模型可实现实际深度和位姿变换的估计。Shen等[18]将极线几何约束引入到自监督学习框架中，但该方法需要预先提取图像特征并匹配特征点。Godard等[19]提出的Monodepth2模型是目前精度最高的自监督学习方法之一，该方法在模型中引入了最小化投影和自动遮罩损失，用来解决场景运动和目标遮挡问题。上述模型仅在空间尺度上采用双目基线约束，尚缺少在视频时间序列上的一致性约束。另一方面，与当前研究[14-19]主要面向的城市道路环境不同，温室环境狭窄拥挤，遮挡严重，作物植株颜色、纹理单一，该类方法在温室移动机器人位姿估计及轨迹跟踪上的适用性值得进一步深入研究。

鉴于以上问题及温室移动机器人自主导航作业的实际需求，在双目基线约束[15]基础上，将时序深度一致性约束引入到学习框架中，提出一种自监督位姿变换估计模型，该模型可用双目视频序列进行训练。针对研究中发现的用帧间静止样本训练模型会造成其位姿变换估计值收缩的问题，提出采用软遮罩来抑制此类样本误差梯度回传的处理方法。在现有研究基础上，优化设计神经网络结构。以采集自种植作物为番茄的日光温室视频数据为例，定义模型性能的判别标准，开展训练与测试试验，验证模型的有效性。

1 自监督位姿变换估计模型的提出

1.1 基于时序图像的自监督位姿估计

在运动相机采集的连续视频序列中，Is、It为相邻视频帧，其中Is记为源图像，It记为目标图像。设空间点P同时出现在相邻帧中，且在Is、It上的投影像素坐标分别为ps和pt，K为相机内参矩阵，Tt→s为相机在It和Is成像状态之间的位姿变换矩阵，根据多视几何，式（1）成立

式中Ds(ps)、Dt(pt)分别表示ps、pt对应的空间点P的深度。当ps、pt用齐次坐标表示时，有式（2）

式中～表示在齐次坐标系下等价。设K已知，根据式（2），由Tt→s和It对应的深度图Dt，It上的像素点可投影到Is上。在Is上对投影点周围采样可重构目标图像，简记为为采样运算[20]，proj为式（2）所示的投影运算，warp 表示投影和采样的复合运算，K则被作为warp的内部信息。

1.2 表观差异度量函数

由pe度量的图像重构误差，以及由此回传的误差梯度是DNN优化训练的关键。根据现有研究[18-19]，用图像像素空间的L1（1范数）距离和结构相似度指数（Structural Similarity Index, SSIM）[21]的线性组合来定义pe函数，如式（3）所示，其中SSIM在块级别比较图像的亮度，以及对亮度变化不敏感的对比度和结构特征相似性。

式中i为像素索引，α为线性组合的比例系数。

1.3 模型约束条件

1.3.1 双目基线约束及软遮罩的提出

由图1可以看出，等比例缩放图像深度和相机光心间的距离，It与Is间的投影关系保持不变，即模型对Dt及Tt→s的预测是相互耦合的，在无额外约束条件下，fD、fP无法预测深度及位置变化的绝对值。双目相机左、右目间的位姿变换矩阵Tl→r为已知，即左目相对于右目在x方向上平移了一个基线距离，本研究用该基线距离作为约束条件，用双目视频序列作为训练样本。将k时刻左目图像作为目标图像，记为，将k时刻右目图像和k-1时刻左目图像作为源图像，分别记为和，基于fD对的深度图，以及fP对左目相机在k和k-1时刻间的位姿变换矩阵的预测，分别在上采样重构目标图像，即有，并以式（4）作为fD和fP的联合优化目标

因Tl→r已知，以为目标，将使fD对的预测趋于实际值，同时以为目标，将使fP对的估计趋于实际值。

在温室场景中，如果相机静止，且当前场景不因外部因素扰动而发生变形，则相机采集的相邻视频帧图像是相同或相似的，称这样的相邻双目视频帧为帧间静止样本（静止帧）。根据式（2），如果以式（4）第2项为模型优化训练目标，无论fD是否正确预测了图像深度，fP只需将帧间位姿变换预测为0，即可使该目标最小化，从而可能使fP的网络参数向预测结果为0的方向塌缩，影像模型训练。网络参数主要受模型误差梯度驱动，为避免静止帧对训练产生的影响，本研究提出用式（5）形式抑制该类样本的回传梯度

1.3.2 时序深度一致性约束的提出

1.4 非刚体场景及遮挡像素处理

图2模型在2个假设上构建：1）场景为刚体；2）场景中可视目标物之间无遮挡。当假设满足时，通过对深度及位姿变换的精确估计，目标图像才可完全从源图像采样重构。当假设不满足时，将产生问题梯度，影响模型训练。作物植株为柔性材料，受风或机器人扰动，场景内部分目标物可能并非绝对静止。同时，温室空间有限，株形复杂，相互遮挡严重。为提高模型训练的鲁棒性，需要对图像中非静止和遮挡区域进行处理，本研究模型除了预测深度及位姿变换外，还为每个重构目标图像预测一个归一化遮罩平面，用以标识因非刚体或遮挡而不能从源图像采样重建的目标图像区域（对应中像素值低的区域），并将其从pe度量中排除。通过式（6）所示的加权表观差异度量函数wpe来实现该处理

1.5 重构目标图像表观差异及约束损失定义

根据以上优化目标及约束条件，定义模型的重构目标图像表观差异及约束损失Lpr如式（7）所示

式中λ、ζ为各项比例调整系数，分别为重构图像和对应的归一化遮罩平面。系数λ用来调整k-1时刻左目图像深度预测训练对模型参数修正的贡献程度。

2 模型的网络结构设计

2.1 网络总体结构

用U-Net[22]架构的卷积自编码器（Convolutional Auto-Encoder, CAE）作为构建fD的DNN网络（图3a）。CAE由编码器和解码器构成。在解码器上设置深度预测分支，该分支包含1个卷积核大小为3×3、输出通道数为1的卷积层（conv 1, 3×3），其以解码器特征图作为输入，输出特征图u经Sigmoid函数激活后作为对的逆向深度的预测，然后用式（8）所示的变换作为对深度图的预测结果

式中a、b为变换系数，该变化可将深度约束在范围内。与用独立DNN预测遮罩平面的方法[12]不同，为降低模型复杂度，本研究进一步用fD预测重构图像的归一化遮罩平面，且遮罩平面预测分支的结构与深度预测分支相同。通过预测多尺度深度图来消除采样运算 的梯度局部性问题[16]，分别在空间尺度为输入图像1、1/2、1/4和1/8的解码器特征图上设置预测分支，预测对应尺度的深度图和归一化遮罩平面。同时，fD以参数共享的方式预测的深度图和重构图像的归一化遮罩平面

fP（图3b）采用与fD相同的CAE结构，与fD不同的是，fP的解码器仅为重构图像预测多尺度归一化遮罩平面，并在编码器末端连接一个位姿预测分支（Pose Estimation Branch, PEB），该分支采用与文献[19]相同的结构，用于预测间的位姿变换矩阵PEB的最后一层为不包含任何激活函数的conv 6, 1×1，其输出特征图经全局平均池化后生成6维向量，其中3维作为以欧拉角表示的帧间姿态变换，另外3维作为在3-D空间上的位置移动，该6维向量可直接转换[19]为。Godard等[23]研究表明，以同步双目图像作为深度预测网络的输入，可提高深度预测精度，本研究采用该方法，以期通过提高深度预测精度来间接提高位姿估计精度。fD、fP映射的最终形式分别为

按Godard等[19]的方法，将多尺度深度图及归一化遮罩平面上采样到输入图像尺度后，按式（7）分别计算各尺度重构目标图像表观差异及约束损失，结合边缘感知深度平滑约束[16]，定义模型总损失Lt如式（9）所示

2.2 星型扩张卷积设计及卷积自编码器构建

在相同计算代价下，扩张卷积（Dilated Convolution, DC）[24]可显著扩大卷积运算的感受野，这有利于在特征图上建立远程空间相关性，该相关性可能对深度预测[25]及位姿估计[14]具有促进作用。但现有研究[26]也表明，DC会使稠密预测结果产生网格伪影，虽然混合DC可解决该问题，但单层孔洞型卷积核仍无法充分提取和聚合输入特征图的局部特征。本研究提出一种新的星型扩张卷积（Star DC, SDC），其卷积核由中心的3×3实心核及8个方向的1-D（1维）核构成，该核可有效提取图像局部特征，且具有较大的感受野。与相同感受野大小的标准卷积相比，SDC可有效降低卷积运算量。SDC不需要修改或扩展现有神经网络计算框架，其可通过扩张率连续的3×3 DC运算叠加构成（图4），如1-D DC运算叠加可表示为式（11）

式中s为输入信号，g为输出信号，r为扩张率，hr表示扩张率为r的1-D卷积核，q为元素索引，G为用于叠加的DC组数。相应的，2-D SDC运算模块可由扩张率连续的G个2-D DC叠加构成，将G作为SDC的超参数，各DC在相同输入特征图上运算，产生的多组特征图通过面向元素（element-wise）求和方式进行叠加，生成叠加特征图，该特征图经激活后作为SDC的输出。为降低SDC的运算量，为各DC采用深度化卷积（Depthwise Convolution, DepthConv）[27-28]形式。

进一步用反向残差模块（Inverse Residual Module, IRM）[29]结构来降低计算资源需求量[30]。用SDC替代标准IRM中的DepthConv层来构建基于SDC的IRM，称为SDC-IRM（图5）。SDC-IRM的输入特征图通道数及IRM扩展因子超参数S[29]决定了SDC的特征图通道数，即SDC的宽度。当SDC的超参数 1G=时，SDC-IRM等同于标准IRM。

以计算机视觉任务中广泛采用的残差网络（Residual Net, ResNet）[31]为基本架构，并用SDC-IRM取代ResNet的常规残差模块来构建CAE（图6）编码器，称为ResNet-SDC。在构建ResNet-SDC时，固定各卷积模块的宽度（模块的输出特征图通道数）比，即首端标准卷积模块和后续SDC-IRM之间的宽度比，与标准ResNet架构中的对应比例相同，因此网络宽度将由首端模块的宽度C决定，称C为ResNet-SDC的超参数。此时，ResNet-SDC的结构由ResNet架构类型，如ResNet-18[31]，超参数C，以及各SDC-IRM模块的超参数S和G决定。解码器由转置卷积（Transposed Convolution, TransConv）和标准IRM模块构成，通过TransConv逐步上采样输出特征图的空间尺度，并通过元素级求和方式，融合编码器同维度的输出特征图。用于多尺度逆向深度图和归一化遮罩平面预测的分支设置在解码器对应尺度的IRM模块上，fP的PEB则以编码器最后一个SDC-IRM的输出特征图作为输入。除预测分支外，网络中各卷积层均配置批归一化（Batch Normalization, BN）[32]，并用Leaky-ReLU[33]作为激活函数。

3 试验方法

3.1 温室环境双目视频数据采集

双目视频采集设备为Stereolabs ZED 2k立体相机，其左、右目分辨率均为1 920×1 080像素，有效采样距离为0.3～20.0 m。用MATLAB R2018a的立体相机标定工具箱标定相机，获取其内、外参数（含K及双目基线距离）。2020年1月和11月，于晴朗天气的9:00－15:00时段，分别在沈阳农业大学实验基地某辽沈IV型节能日光温室和沈阳市辽中区某实际生产用日光温室中进行视频采集，温室种植作物均为番茄，植株吊蔓生长，其中前者温室处于坐果期，株高1.8～2.3 m，行距约1.0 m，株距约0.3 m，后者处于花期，株高1.3～1.5 m，行距0.8～1.0 m，株距约0.3 m。

共采集3类视频。首先将相机置于手推式小车上，沿株行间和人行通道随机行走，行进过程中采集视频，并通过调整相机角度来增加样本视角多样性。将采集的视频分割成小序列，每个序列包含200帧双目图像，共计500个序列，构成集合A。然后将相机固定于带刻度平直滑轨的可移动滑块上，在温室多个位置固定滑轨，移动滑块并采集视频，移动过程中，相机在滑块上姿态（角度）固定，即相机仅产生位置变化，每次采样生成1个视频序列并记录滑块滑动距离，共采集200个序列，构成移动距离已知的集合B。进一步将相机固定于三脚架顶部具刻度、可360°旋转的载台上，在温室多个位置放置三脚架，转动载台并采集视频，转动过程中，相机相对于载台位姿固定，每次采样生成1个视频序列同时记录载台转动角度，共采集200个序列，构成转动角度已知的集合C。可将集合A采集时的相机运动视为不规则运动，集合B、C视为规则运动。集合A、B、C共同构成温室环境双目视频数据集。

3.2 模型的训练与测试方法

用Microsoft Cognitive Toolkit (CNTK v2.7)[34]实现本研究模型，用Adam优化器[35]对其进行训练。根据相机有效采样距离，式（8）中的变换系数设置为 3.28a=、b= 0.05。根据预试验，损失函数中各项系数分别设置为α= 0.85、ϑ= 5、λ=1、ζ=1、μ= 5，网络权重衰减因子设为5×10-5，可取得较好的效果。初始学习率为10-4，每经20代（epochs）迭代训练，学习率下降为原来的1/10[19]，预试验表明经过40代迭代训练，模型损失可收敛到稳定值。模型输入图像设置为512×288像素。训练过程中，用数据增广方法来提高样本多样性，该方法可在不增加样本采集工作量的前提下，提高模型泛化效果。首先把1个视频序列的当前帧作为目标图像，再从其前后3个连续帧中随机选择1个作为源图像，构成一个样本，该过程可增加帧间位姿变换的多样性。接着随机决定是否对该样本图像做水平翻转或垂直翻转，并进一步按文献[25]方法对每对目标图像和源图像的亮度、对比度和饱和度在[0.8, 1.2]范围内做相同随机调整。数据增广中所采用的随机过程均服从均匀分布。

在NVidia Tesla K80计算卡上开展训练及测试试验，试验用计算机配置为Intel Xeon E7-4820 v3处理器，128GB内存，Windows Server 2012 R2操作系统。采用简单交叉验证来评估模型，每次试验分别从集合A、B、C中随机选择80%、50%、50%的样本序列作为训练集，使训练集样本数不低于数据集样本总数的2/3，其余作为测试集。为提高评估可靠性，每个模型试验重复5次，最后用各指标均值来评价模型。在对模型进行测试时，仅将图像调整为输入尺寸，不对测试样本进行数据增广。

3.3 模型评估标准

本研究用移动距离和转动角度已知的B、C测试集视频序列来评估模型精度。如果在不规则运动的A类视频占多数的训练集上训练的模型，能够准确预测规则运动的B、C测试集的位姿变化，即可说明模型的泛化性能。对于有n帧图像的序列j，相机末帧相对于首帧的位姿变换估计为为模型估计的m和m-1帧间的位姿变换矩阵。是帧间位姿变换的累积，是变换的宏观表现，因此可用其评估模型位姿估计和轨迹跟踪的精度。可分解为位置变换和以轴角表示的姿态变换。设B测试集有N个序列，序列j记录的相机实际滑动距离为lj，用各序列和lj的平均相对误差（Mean Relative Error, MRE）、平方相对误差（Squared Relative Error, Sq Rel）、均方根误差（Root Mean Squared Error, RMSE）和lg化RMSE（lg RMSE, RMSElg）来评估模型位置估计精度。各指标定义如式（12）～（15）

相机在平直滑轨上移动时，模型估计轨迹应该是平直的，该平直性用视频序列的估计轨迹与首末帧估计坐标构成的直线之间的决定系数R2来衡量，进而用N个序列的平均决定系数（meanR2, mR2）来衡量模型估计轨迹的稳定性。同时，固定在滑块上的相机在平直滑轨上移动时也不应有姿态角变化，如存在该变化，则被视为随机误差，进一步用平均每百帧累积姿态角误差（Mean Cumulative Rotation Error per Hundred Frames, MCRE）来衡量模型的稳定性。C测试集中，序列j记录的相机实际转动角度为rj，模型估计姿态角变化为，用各序列和rj的MRE、Sq Rel、RMSE和RMSElg来进一步评价模型姿态估计的精度。

4 模型的测试结果与分析

4.1 不同处理对模型性能的影响分析

为分析不同处理对模型位姿估计精度的影响，通过启用或关闭不同处理，构建了8种模型（表1）。其中软遮罩处理，指在和的表观差异度量中用pe'函数，如不启用，则采用pe函数。归一化遮罩处理指在模型中预测归一化遮罩平面，并在损失函数中使用wpe。星型扩张卷积处理指在SDC模块中采用r连续变化的DepthConv，否则各DepthConv的r值均为1，此时SDC退化为DepthConv。双目输入指fD的输入为同步双目图像，否则仅输入目标图像。特征丢弃处理指在PEB前采用丢弃（Dropout）层，按30%的比例丢弃fD编码器传入的特征[36]。时序一致性处理指fD共享参数方式预测源图像深度，并进行时序深度一致性约束，如不启用，则模型中无此约束，相当于λ=0、ζ=0。首先以ResNet-18作为参考架构，并设置ResNet-SDC的超参数C=48来构建CAE编码器，其中SDC-IRM的超参数设为S=1、G=6，解码器中的IRM超参数S=1。对各模型采用相同的训练 和测试方法，结果如表2。

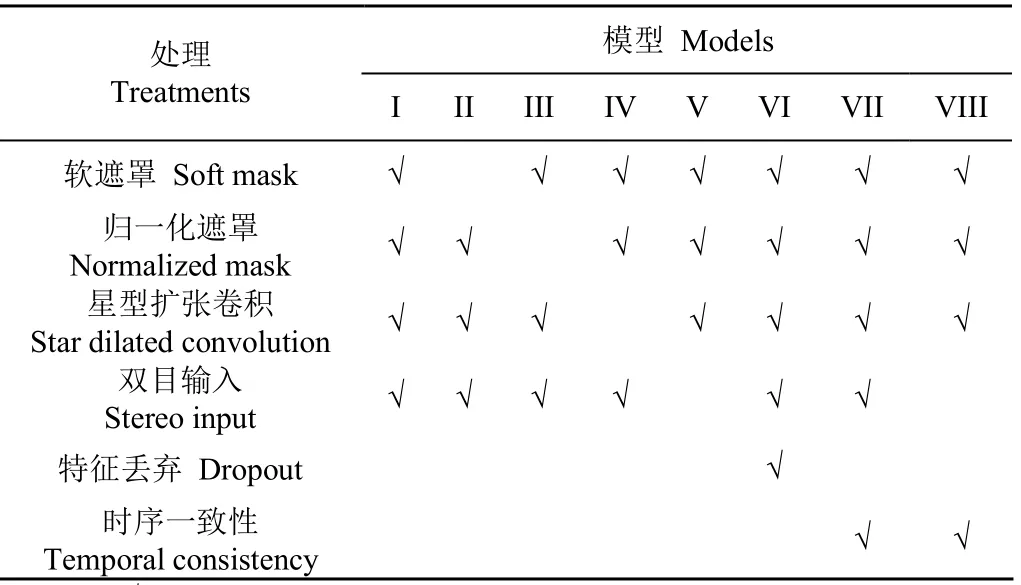
表1 不同处理的深度及位姿估计模型 Table 1 Depth and pose estimation models with different treatments

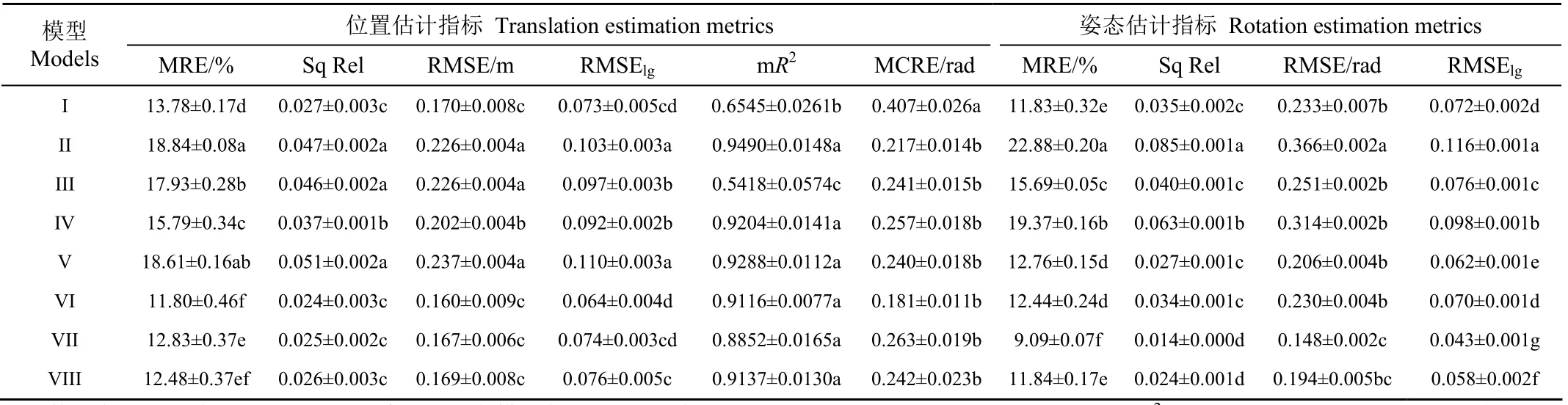
表2 不同模型的位置及姿态估计性能比较 Table 2 Pose estimation performance comparison between different models

由表2可知，不同模型在位置及姿态估计性能上具有较大差异。模型I在II的基础上启用了软遮罩，该处理使I的4种位姿估计误差指标均显著降低，其中位置估计MRE减少了5.06个百分点，姿态估计MRE减少了11.05个百分点，RMSE则分别降低了24.78%和30.65%，表明软遮罩处理能够有效提高模型精度。如不启用软遮罩，当训练集中存在静止帧时，无论fD的深度预测结果如何，fP对位姿变化的预测趋近于0，都可以使以pe为代价的损失最小化，从而使fP网络参数向输出为0的方向更新，出现预测值收缩问题，这是模型II精度低于模型I的原因。软遮罩可抑制静止帧产生的网络参数修正，也会对网络训练产生一定影响，即模型对帧间不明显位姿变化不敏感，会产生较大的系统随机误差，这也是模型I的mR2和MCRE指标比II差的原因。

I在III的基础上采用归一化遮罩，该处理使I的4种位置和2种姿态估计误差显著降低，其中MRE分别减少了4.15个百分点和3.86个百分点，mR2显著提高。用归一化遮罩抑制无法采样重建的目标图像区域的表观差异度量，使模型有机会考虑并处理非刚体及场景遮挡问题，避免了问题梯度回传，使模型更具鲁棒性。I在IV的基础上，在网络中启用了SDC，在网络参数不变的前提下，该处理使4种位置估计误差和3种姿态估计误差显著降低，其中I的姿态估计MRE在IV的基础上减少了7.54个百分点，同时RMSE也有所降低，表明本研究设计的SDC模块能够有效提高模型位姿估计的精度。SDC扩大了卷积核的感受野，可使编码器在特征图显著降维前，建立起远距离特征点的空间相关性，这对位置及姿态估计都具有重要作用。

I在V的基础上，对fD采用双目输入，该处理使I的4种位置估计误差显著下降。VII在VIII的基础上采用双目输入，使VII的姿态估计MRE和RMSElg误差显著下降，Sq Rel和RMSE有所降低，表明双目输入对提升模型位姿估计精度具有一定作用。以双目图像作为输入，能够有效提高深度估计精度[23]，由fD和fP的耦合性，fD性能的提高，对fP也具有促进作用。VI在I的基础上，在PEB前启用了Dropout，该处理使VI的位置估计MRE显著下降，mR2显著升高，MCRE显著下降，姿态估计MRE显著升高，其他各项误差指标有所下降，表明Dropout对提高模型精度具有一定效果，对提高模型稳定性具有显著作用，这和Dropout迫使网络学习更加鲁棒性的特征有关。VII在I的基础上启用了时序一致性约束，使VII的位置估计MRE和姿态估计的全部4种误差显著下降，其中姿态估计MRE减少了2.74个百分点，RMSE降低36.48%，同时mR2显著提高，MCRE降低了54.75%，表明本研究提出的时序一致性约束对位姿估计精度和模型稳定性都具有显著提升作用。对帧间时序深度进行一致性约束，该一致性也会间接传导到fP中，从而使位姿预测更加稳定。总体而言，相较于其他模型，VI和VII具有更高的综合位姿估计性能。

4.2 网络结构对模型性能的影响

为进一步分析网络结构对模型性能的影响，通过调整CAE编码器的参考架构、ResNet-SDC的超参数C、SDC-IRM的超参数S和G，以及PEB的宽度（分支中除conv 6, 1×1之外其他各层卷积的通道数），构建了9种网络结构（表3）。与模型I相比，VI和VII启用多种处理，具有更高的性能，但也需要更多的存储和计算资源，与网络2结合时，超出了试验设备的处理能力，因此本 研究在资源需求相对较低、性能相对较高的模型I基础上应用这些网络，开展训练和测试试验，用于分析网络结构对模型性能的影响，结果如表4。

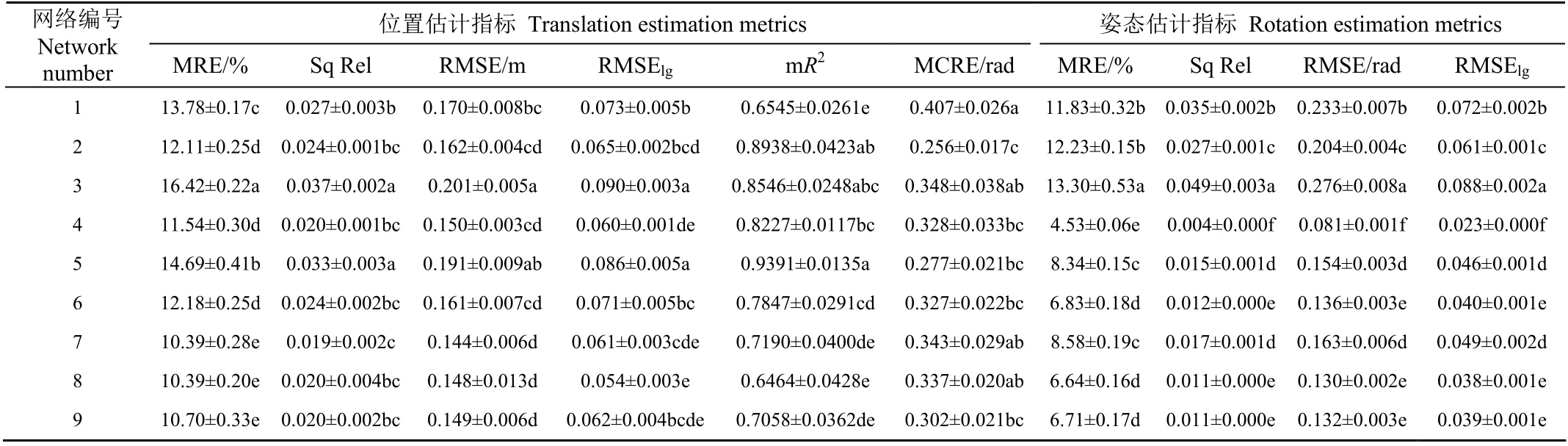
表4 网络结构对位姿估计性能的影响 Table 4 Effect of the network structure on performance of pose estimation

表4数据表明，网络结构可显著影响模型I的位姿跟踪性能。与网络1比，2采用ResNet-50参考架构，增加了编码器深度，使模型位置估计MRE和姿态估计的3种误差显著下降，mR2显著提高、MCRE显著下降，表明增加编码器深度可提高模型位姿估计性能及稳定性。这主要是随着网络深度增加，编码器的图像特征提取能力增强，但同时网络计算复杂度也会增加。网络3在1的基础上扩大了C值，增加了网络宽度，但除mR2显著提高、MCRE显著降低，即模型稳定性增加外，其他位姿估计误差都显著增加了，表明简单增加网络宽度无法提高模型性能。这和SDC-IRM的结构和其超参数设置有关，IRM允许用较窄的瓶颈层[29]，且由于网络3中的S=1，仅增加C，并不能显著增加SDC的宽度和其图像特征提取能力。相较于网络1，4增加了S值，使模型的位置估计MRE和 RMSElog显著降低，mR2显著提高，MCRE显著下降，其中姿态估计MRE减少了7.30个百分点，达4.53%，模型精度及稳定性显著提高。S值增大，有效增加了SDC-IRM中SDC模块的宽度，可提高其特征提取和模型表达能力，进而提高了模型的位姿估计性能。

网络5在1的基础上，增加了G的值，虽使位置估计误差升高，但mR2显著增加，MCRE显著下降，姿态估计误差也显著降低，说明继续增大SDC感受野对模型性能仍有一定促进作用，但该作用主要集中在对姿态估计精度和模型稳定性的提升上。网络7、8、9的比较也表明，增加G值，主要促进姿态估计精度的提升。当G=6时，进一步增加G，对模型性能的提升已无显著作用，表明此时SDC的感受野大小已能满足相关点建立空间相关性的需求，继续增加G值，SDC的特征响应值中包含了大范围内的无关特征，反而会影响模型性能。相比网络1，6增加了PEB的宽度，使后者位置估计的MRE显著下降，mR2显著升高，MCRE显著降低，姿态估计精度显著提高，表明增加PEB宽度对提高模型位置估计性能和稳定性是有效的。综合各项指标，针对模型I，在ResNet-18参考架构下，网络4和8具有更高的位姿估计精度。

4.3 方法比较与分析

Monodepth2[19]是目前精度最高的同类型深度及位姿估计模型之一，该模型同样可采用双目视频序列进行训练，其以标准ResNet-18作为CAE编码器，解码器则由最邻近插值上采样和常规卷积构成。本研究方法组合综合性能较高的模型VII和网络4，且在PEB前启用Dropout。同时添加2种组合，组合1用模型VII和Monodepth2的网络结构，组合2用Monodepth2模型和本研究网络。开展训练和测试试验，同时用计算速度衡量位姿估计网络（由fP的编码器和PEB构成）的实时性，不同方法的性能比较结果如表5。

由表5可知，本研究方法的位置和姿态估计MRE分别为8.29%和5.71%，与Monodepth2相比，分别减少8.61个百分点和6.83个百分点，RMSE则分别降低45.98%和49.78%，除mR2和计算速度外，其他各项误差指标均显著低于后者，表明针对种植作物为番茄的温室环境，本研究方法在位姿估计上具有更高的精度。本研究网络计算速度为56.5帧/s，具有实时性，由于SDC是通过多组DepthConv叠加构成的，速度上低于单层常规卷积，因此整体计算速度低于Monodepth2。本研究方法和组合1的模型相同而网络不同，对比表明，除mR2和MCRE外，前者其他各项误差指标均显著低于后者，表明本研究网络具有更高的位姿估计精度。对比Monodepth2和组合2，后者各项误差显著降低，mR2均值有所增加，进一步表明本研究网络的有效性。与常规残差模块相比，本研究网络的SDC-IRM具有更大的单层感受野，有利于在更大尺度范围内搜索图像的空间相关性，这是本研究网络能进一步提升模型精度的主要原因。对比本研究方法和组合2，除mR2和MCRE无显著差异外，前者其他各项误差指标均显著低于后者，表明本研究在模型中引入的多种处理对提高温室移动机器人位姿估计性能是有效的。

进一步在A、B、C测试集上，对各方法的深度估计性能进行比较。用点i的估计深度和通过文献[25]方法获得的实际深度Dt（i）的MRE、Sq Rel、RMSE、RMSElg，以及阈值限定精度，即满足的点所占的比例，其中[19]，来评价模型深度估计性能，同时评估深度估计网络fD的实时性，结果如表6。

表6 不同方法间的深度估计性能比较 Table 6 Depth estimation performance comparison between different methods

由表6可知，本研究模型在20 m采样范围内，其深度估计MRE为11.35%（<11.4%），RMSE为0.528 m（<0.53 m），计算速度为31.9帧/s，具有实时性，与Monodepth2相比，前者的各项误差均显著降低，阈值限定精度显著升高。除模型和网络结构差异外，本研究采用同步双目图像作为fD的输入，该处理可有效提高深度估计精度[23]，由fD和fP的耦合性，其可进一步促进位姿估计精度的提高，这也是本研究模型位姿估计误差低于Monodepth2的另一个原因。对比本研究方法和组合1，以及Monodepth2和组合2，结果表明本研究网络同样可提高深度估计精度。SDC的卷积核结构可同时提取局部图像特征并建立起特征点间的远程空间相关性，这一特性对位姿及深度估计性能的提升均是有效的。组合1的各项深度估计误差均显著低于Monodepth2，表明本研究在模型中引入的多种处理对提高深度估计精度也是有效的。

采用本研究模型对测试集中部分视频序列的相机轨迹进行估计，并在视频序列首帧对应的场景中渲染部分轨迹点，同时估计首帧图像的深度，结果如图7。

图7表明，模型能够对相机运动轨迹进行有效跟踪，并能估计每帧图像对应的深度。图7a对应的视频序列为相机沿行间通道行进至温室后保温墙前折返，模型估计的运动轨迹及部分轨迹点与该过程是相符的。图7b对应的视频序列为相机在行间通道右侧行进至保温墙前的人行通道，左转并继续前进，从模型跟踪轨迹来看，与该过程也是相符的。图7c为相机沿植株行间通道行进至保温墙前右转，模型所跟踪的运动轨迹变化趋势与相机对应的运动过程也是相符的。图7d为相机在平直滑轨上前向移动1.2 m，从模型跟踪的相机轨迹及轨迹在x，z平面上的投影可以看出，轨迹长度与移动距离相符，且跟踪轨迹平直，表明本研究模型具有较好的稳定性。采样设备为双目相机，模型跟踪的是左目相机的运动轨迹，图7d中部分轨迹点与滑轨的相对位置关系也与该情况相符。图7同时表明，模型能够估计图像对应场景的深度，其对株行间通道和目标物远近都给出了较好的预测。位姿跟踪与深度估计能为vSLAM提供支撑，这为模型应用于温室移动机器人自主作业提供了可能。

5 结 论

面向温室移动机器人自主作业实际需求，提出一种基于时序一致性约束的自监督位姿变换估计模型。以采集自种植作物为番茄的日光温室视频数据为例，开展训练和测试试验，结论如下：

1）用软遮罩将视频序列的静止样本从图像表观差异度量中去除，模型的位置和姿态估计相对误差MRE分别减少5.06个百分点和11.05个百分点，均方根误差RMSE分别降低24.78%和30.65%。在模型中用归一化遮罩来处理非刚体场景和目标遮挡问题，位姿估计MRE则分别减少4.15个百分点和3.86个百分点。2种遮罩可显著提高模型精度。

2）基于星型扩张卷积的反向残差模块在网络参数不变的前提下，使模型的姿态估计MRE减少7.54个百分点，表明该结构对降低模型误差具有显著作用，增加卷积核感受野是提高模型精度的有效手段。

3）时序深度一致性约束使模型对姿态估计的MRE减少了2.74个百分点，RMSE降低36.48%，每百帧累积姿态角误差降低54.75%，该约束可用于提高模型姿态估计精度及稳定性。

4）扩大反向残差模块的扩展因子可显著降低位姿估计误差，姿态估计MRE减少了7.30个百分点。增加星型扩张卷积核的感受野能够提升姿态估计精度，但当最大扩张率超过6时，其作用不再明显。

5）本研究位置和姿态估计MRE分别为8.29%和5.71%，与Monodepth2相比，分别减少了8.61个百分点和6.83个百分点，模型精度显著提高，模型能够对相机行进过程中的轨迹进行有效跟踪。位姿估计网络计算速度为56.5帧/s，具有实时性。该方法可为温室移动机器人导航系统设计提供支撑。