基于改进多父辈遗传算法的农机调度优化方法

张 帆，罗锡文，张智刚，何 杰，张闻宇

（华南农业大学工程学院，南方农业机械与装备关键技术省部共建教育部重点实验室，广州 510642）

0 引言

传统农机跨区作业存在组织效率低、劳动生产率不高等问题，造成资源浪费[1]。农机作业时效强，特别是在农忙时节，要求农机在规定时间内完成作业任务，以确保粮食归仓和及时播种，提高农机作业效率已经成为农业生产的首要问题。农机导航技术与物联网技术的兴起，为农机规模化调度和农场规模化作业的实现提供了技术支撑，加速了传统农机作业迈向智能农机作业的进程[2]，也为无人农场的建设运营提供理论依据[3-4]。

在农业生产过程中，随着对自动导航作业需求的不断增加，实现多台同种或异种作业农机之间协同作业已成为农机导航研究的重点[5]。对于单作业任务而言，国内外对农机的协同作业的研究重点主要集中收获农机与运输车辆之间的配合作业上[6]，如Lida等[7]和Noguchi等[8]分别研究了农机车辆自动跟随作业与协同导航作业操作的问题。Zhang等[9]开发了一套跟随式农机主从导航作业系统，实现了从机对主机的辅助运输和加油等作业。针对多作业任务的需求，通常要根据机器、人员以及作业任务等信息，设计优化算法与决策策略，科学地对机器和人员进行运营调配，在保证所有作业任务及时完成的前提下，实现作业时间最短或作业成本最小[10-11]。

国内外许多学者对多农机执行多种作业任务的资源配置问题进行了研究。Jena等[12]利用混合整数规划的方法确定甘蔗收获机的作业路径；Sethanan等[13]以甘蔗收获机作业距离最小化和甘蔗收获产量最大化为目标，提出了改进粒子群优化算法（MO-GLNPSO）解决甘蔗收获机路径规划问题；Pitakaso等[14]提出了一种基于时间窗的联合收获机分配与路由问题的领域搜索方法，在联合收获机在任务共享的情况下，最大限度地提高收获机的服务面积；Cerdeira等[15]研究了一个具有附加集群约束、时间窗和城市处理时间约束的旅行商问题（Traveling Salesman Problem，TSP）的变换模型[16]，并采用禁忌搜索和模拟退火思想相结合的算法对一个农机合作社几个联合收获机的作业路径进行了优化。国内方面，曹如月等和张小花等类比旅行商问题[17-18]，采用蚁群算法求解多机协同作业任务规划问题，但未将农机在田间作业的约束进行综合考虑；He等[19]提出了一种基于禁忌搜索和遗传算法算子的混合算法以确定小麦的最优收获时间，达到减少收获时间的目的；王雪阳等[20]采用改进遗传算法对跨区域作业的农机调度问题进行了研究；Zhou等[21]采用粒子群算法和遗传算法相结合的方法求解了农机调度服务问题。部分研究采用启发式算法，如吴才聪等[22]针对单一农机的作业问题建立了时空调度模型，并以动态规划的方式进行基于时间窗的分步求解，最终完成整个模型的调度；Zhang等[23-24]针对农机跨区紧急作业调度问题进行了模型设计，并采用基于距离最近优先的多机多任务紧急调配和基于贡献度最大优先的多机多任务紧急调配的启发算法进行了求解，完成了农机的调度任务。

上述研究对多农机在特定时间内完成同一种作业任务提供了很好的解决方案，但是对农机作业过程中多种任务连续作业的问题，如需连续进行耕整、播种和施肥等作业，无法提供科学合理的决策服务。本文主要研究多农机多任务的连续调度问题，综合考虑了调度损耗与作业损耗，通过采集的任务与农机的作业参数，建立农机调度模型，以作业时间最短为优化目标，利用改进的多父辈遗传算法进行农机作业任务序列规划，为解决多任务多农机的调度问题提供理论依据，也为开发基于无人农场智能农机管控平台提供决策参考。

1 多农机多任务作业调度问题

1.1 问题描述

随着3S技术[25]与农机自动驾驶技术[26]的不断发展，智能农机可通过移动互联网与云平台进行实时通讯，将农机的实时位置、速度、作业等信息上传至云端，这为农机的精准调度提供了数据参考与技术支撑[27-28]。农机作业具有很强的时效性，特别是在农忙时节，需要在较短的时间内完成农田的耕整、播种、施肥等作业操作，而进行每种作业的农机具也各不相同，这就要求在有限的作业期限内做出科学的农机作业调度决策，在保证作业任务及时完成的前提下，实现作业成本最小化[29-30]。

在农机调度中，单机单任务的农机作业序列规划问题可类比成TSP问题进行分析，对农田空间分布和农机作业时间进行综合考虑；而对于多机多任务的农机作业序列规划问题，可描述为：m台能执行不同作业任务的农机需要在n块农田上进行特定作业，指定每块农田特定的作业任务及顺序、每块农田作业参数及每台农机的参数，安排每台处于不同位置的农机在不同田块的作业任务和作业顺序，使整个农场的生产作业耗时达到最短。此外，本研究还综合考虑了农机从当前位置到目标田块的迁移时间，以及农机在达到目的地后作业准备时间。

1.2 数学规划模型

根据多机多任务调度问题的描述，对该问题的抽象模型定义如下：

1）农田集合F={F1,F2,…,Fm}，以Fi代表第i块农田，其属性描述为Fi={LocFi,SFi}，其中LocFi和SFi分别表示农田Fi的入口位置和面积，

2）农机集合M={M1,M2,…,Mr}，以Mj代表第j台农机，其属性描述为Mj={LocMj, RSj, WSj，ReadyTj}，其中，LocMj表示农机Mj的当前位置，RSj表示农机Mj地块转移过程中的平均行驶速度，WSj表示农机Mj的平均作业速度,ReadyTj表示农机作业前准备时间，且有 [1,]jr∈ ；

3）农机集群MT={MT1,MT2,…,MTn}，以MTk代表第k种类型农机，表示为MTk={Mk1,Mk2,…,Mka}，a为第k种类型的农机总数，且有

4）作业任务序列的集合Task={Task1,Task2, …,Taskm}，Taski代表农田Fi的作业序列，并表示为Taski={Taski1,Taski2,…,Taskin}，Taskik代表在农田Fi上进行第k种作业，且对应作业的农机类型为MTk，[1,]kn∈ 。

此外，农机调度还需满足下述条件：

1）每台机器只能同时在某一块地上进行作业；

2）在农机数量充足的条件且农田面积大于0.3 hm2时，每块地可安排多台同种作业任务的农机进行作业；

3）为避免不同类型农机因作业任务不同而产生干扰，单块农田只进行同一种作业类型的作业，而需要多机协同完成同一作业任务的情况（如收获机与运粮车的协同收获作业），将其处理成同一类型作业任务；

4）每块农田不同任务的作业顺序固定，须满足专门的作业规程，且每块农田的任务必须被执行。

上述调度问题在考虑农田作业任务要求的同时，还考虑农田与农机的相对位置关系，以最近距离农机优先作业为原则，求出每块农田上农机的作业顺序集Si={Si1,Si2,…,Sir}，并以Sij表示农机Mj到农田Fi的调配方案，选取总调度时间最小为优化目标，调度模型表示如下：

调度目标：

约束条件：

式中T为任务总时间，h；TiF为第i块农田的作业总时间，h，其中i=1, 2,…,m；transTik为农机集群MTk到农田Fi的转移时间，h，其取值为农机集群MTk中每台农机出发去农田Fi的转移过程中所耗时间的最大值；readyTik为农机群MTk中每台农机到达农田Fi作业前的准备时间，h；workTik为农机集群MTk在农田Fi的作业总时间，h；SiF为农田Fi的面积大小，hm2；Dij为农机Mj当前位置到农田Fi的距离，km，文中采用农机Mj到农田Fi两点之间的距离进行简要计算；Ek为第k种类型农机的工作效率，即每小时的作业面积，hm2/h；zik表示农机群MTk是否在田块Fi进行作业，其中k与任务Taskik相对应，当农田中Fi中有任务需要被执行的任务k时，zik取值为1，否则为0；tij表示农机Mj是否到农田Fi进行作业，若该农机的田间转移时间大于当前已经到达农田Fi的农机集群MTk完成农田任务总时间，则当前农机不参与该地块的作业，此时tij置于0，否则为1；Yi为农田Fi的的任务数量。式（5）表示农田Fi的每个任务都允许有多台农机参与，且每个任务必须被执行。

2 IMPGA算法原理

基于上述数学模型，本文提出了基于时间窗的改进多父辈遗传算法求解多任务多农机调度问题，算法流程如图1所示。

具体算法步骤如下：

1）初始化问题参数集。录入农机、农田、作业任务等基础信息，同时设置种群规模数PopulationNumber和迭代次数Iteration；

2）编码。基于农田序号的编码并初始化种群。

对于m块农田有r种作业任务情况下的作业调度问题，每条染色体的基因数量为个（Ni表示农田Fi的任务个数），使用农田编号进行编码，农田编号在染色体中出现的频次代表农田作业任务号，第x次出现的作业序号代表该农田的第x个作业任务。如在一个2×2的调度问题中，农田集合F={F1,F2}，对应的任务集合Task={(1,2)，(2,3)}，则随机分布的编码共有6种类型，如[1 2 1 2]或[1 1 2 2]等。

3）适应度函数计算。以作业时间最短为优化目标，则遗传算法的适应度函数为

式中f为染色体适应度，依据公式（1）～（5）对每个染色体的适应度值进行计算。

4）个体选择。由于种群中优秀的父代个体中的基因质量更好，为了保证优秀个体基因的遗传，加速寻优结果的收敛速度，按适应度值将种群划分成优秀和良好2种种群，其中优秀种群占总群体规模的1/3，良好种群占2/3，从优秀群体里随机选取个体Parent1，从良好群体随机选取个体Parent2和Parent3。

5）变异。算法设计可调整的变异概率，当在进行多次迭代之后，如果种群中最优染色体的适应度没有发生变化，则调整变异概率，若发生进化，则截至当前未进化的代数index置为0并重新开始累积，调整的变异概率用函数表示为：

式中pm为当前变异概率，%；pm0为初始变异概率，%；index为截至当前未进化的代数。

6）多父辈POX交叉。本文采用黄明等[31]提出的多父辈POX交叉方式，用优秀个体Parent1分别与良好个体Parent2和Parent3进行交叉，产生后代Child1和Child2，以3×3的调度问题为例来说明交叉过程，如图2所示。首先假定有3个选择的染色体序列Parent1、Parent2和Parent3，且有2个非空互余的基因子集Gene1 {1，2}和Jene2{3}；分别将Parent1中Gene1和Gene2进行分离，并将分离的基因原位置于O，O表示该位置暂时为空，再将Parent2和Parent3进行处理，分别保留Gene2和Gene1；最后分别将Parent1中保留的Gene1和Parent2中保留的Gene2进行交叉，即按从前到后的顺序将Parent1中属于Gene1的基因依次放入Parent2中，生成Child1，同理将Parent1中属于Gene2的基因依次放入Parent3中，生成Child2。至此，多父辈的POX交叉的过程结束。

7）迭代进化。判断是否满足算法结束条件，若不满足，则返回至步骤3）迭代；若满足终止条件，则算法终止，输出最优结果，并将最优结果进行解码。

解码是步骤2）的编码逆变换过程，用实例来描述解码过程如下：在一个2×2的调度问题中，农田集合F={F1,F2}，对应的任务集合Task={(1,2)，(2,3)}，农机集合为MT={MT1,MT2,MT3}，其中Task中的1代表平地作业，使用农机群MT1进行作业，同理，2和3分别代表播种作业和施肥作业，相应地使用MT2和MT3进行作业，当染色体编号为[1 2 1 2]时，表示的农田作业次序为F1-F2-F1-F2，则农机调度流程为MT1-MT2-MT2-MT3。在确定农机集群的调度流程后，还需对MTk进行解码。对于任意序列MTk的解码可描述如下：考虑农机数量充足的情况，对处于不同位置的农机，当选择农机集群MTk去同一目标农田Fi进行作业任务Tk时，本文以基于最短路径的贪婪算法选择作业的农机台数，具体过程为：①在农机集合M中筛选农机类型为k的农机集合MTk，分别计算农机Mki到农田Fi之间距离，并按增序进行排列；②以农田Fi的面积SFi为调度约束，依据公式（3）～（5）选择可作业农机，判断某台农机能否加入该农田作业的准则是：若该农机的田间转移时间大于当前已加入集群作业农机完成农田任务总时间，则当前农机不参与该地块的作业。

3 IMPGA算法验证

3.1 试验数据

本文的农田数据采自新疆塔城地区，依据实际作业环境设置仿真作业任务，以验证算法的性能和稳定性。算法的运行环境为：处理器Inter(R)i5-7500 3.4GHz，内存8G，操作系统Windows10，编程语言Java。表1为部分作业农田的基本信息，主要包括农田面积、农田入口经纬度与作业类型。表2为可用农机装备的基本信息，如农机作业效率和路面行驶速度，此外包括每台农机的初始位置经纬度及准备时间，准备时间即农机达到农田后需要进行作业准备的时间，如作业人员就位、装料、加油、机器作业参数调整等作业前准备所需消耗的时间。

表1 部分作业农田的基本信息 Table 1 Basic information of part of farmland

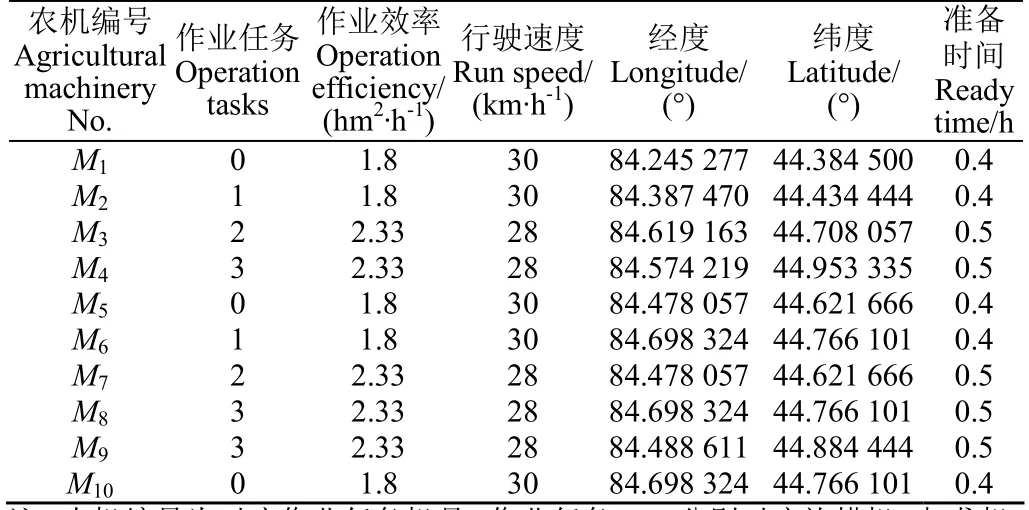
表2 可用农机的基本信息 Table 2 Basic information of available agricultural machine

3.2 结果与分析

对上述农田的作业任务采用改进的遗传算法进行仿真调度试验，选取种群规模为300，进化500代，初始变异概率0.05。完成每种作业农机只有1台时，选取农田数量为6，此时作业任务数量为20个，使用改进遗传算法进行运算得出最优调度方案，再通过Matlab生成甘特图，如图3a所示，其中甘特图白色部分代表农机在田块之间的转移时间与准备时间之和，其他颜色代表了农机在不同农田的作业时间，该调度方案的总完工时间为85.42 h。同理，当执行每种作业任务的农机数量为多台时，调度结果如图3b所示，该调度方案的总完工时间为38.45 h。

为了验证改进遗传算法的有效性和稳定性，首先考虑执行每种作业任务的只有1台时（以下简称单农机作业），选取农田数量为5、10、15和20块的作业任务，分别使用IMPGA和GA进行调配运算10次，调度结果如表3所示。由表3可知，当执行每种任务的农机数量为1台时，改进的遗传算法的最优解、平均解均优于标准遗传算法，其调度时间的最优解和平均解分别缩短2.24%和3.16%，且改进遗传算法的平均标准偏差小，证明了改进遗传算法的鲁棒性好于标准遗传算法；为验证IMPGA的收敛性，对比最优解出现的迭代次数可以发现，除农田数量为15时IMPGA出现的次数大于IG之外，其余农田数量相同的条件下IMPGA均能更早找到最优解，而对比平均值发现，GA最优解平均出现的迭代次数为298.5，而IMPGA为255.8，IMPGA比GA收敛更快。此外，通过对比算法运行时间可知，2种算法的运行时间均随着任务数量的增加而增加，改进遗传算法的平均运行时间比标准遗传算法的平均运行时间长2.36 s。

表3 单农机作业下IMPGA与GA的调度结果对比 Table 3 Comparison of results between IMPGA and GA under single number machinery

由表4可知，当执行每种作业任务的农机多于1台时，作业任务完工总时间小于农机数量为1台的结果。在农机数量相同时，改进遗传算法的调配结果仍优于标准遗传算法的结果：在农田数量为5时，2种算法均能求得最优解；在农田数量为10时，使用改进遗传算法求取调度的最优时间和平均时间分别缩短3.77%和3.56%；农田数量为15时，最优时间和平均时间分别缩短1.63%和3.76%；农田数量为20时，最优时间和平均时间分别缩短4.46%和3.47%。此外，随着农田数量增多时，算法运行时间增加，且改进遗传算法的平均运行时间比标准遗传算法的运行时间长8.92 s。

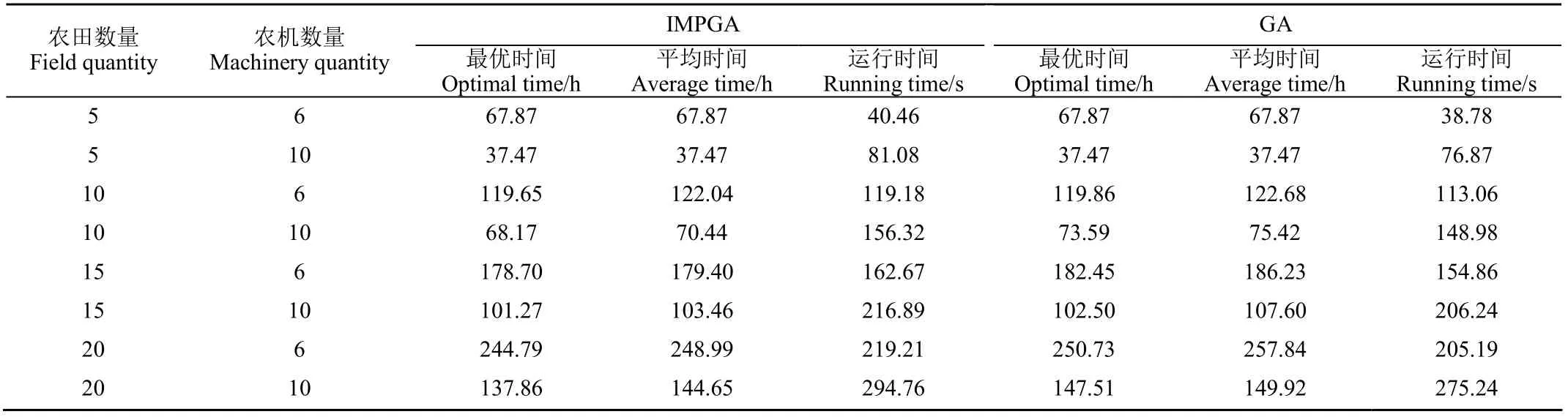
表4 多农机作业的IMPGA与GA调度结果对比 Table 4 Comparison of results between IMPGA and GA under multi-type machinery

总之，本文改进的遗传算法在总体上优于标准遗传算法，其调度的最优时间和平均时间分别能平均缩短2.47%和2.70%，能满足农机作业调度的任务需求。

4 结 论

考虑实际农田作业情况，本文分析了针对连续作业任务的农机作业任务规划问题，在农机随机分布的情况下，以作业时间最短为优化目标，建立了基于农业生产中多机执行多任务的调度模型。在考虑农机田间转移时间和作业准备时间的前提下，采用改进遗传优化算法对多机多任务的农田作业问题进行调配，通过与标准遗传算法相对比，结果表明：改进的多父辈遗传算法能有效解决多任务农机的作业分配问题，在迭代次数相同的情况下，尽管IMPGA比GA运行时间长8.92 s，但IMPGA求解调度方案的最优时间和平均时间分别能缩短2.47%和2.70%，节约了时间成本，满足农机运维和无人农场生产运营实际作业的调度需求。

后续研究将考虑多台农机同时作业，某台农机发生故障时如何对农机重新进行作业分配的问题；此外，随着农机自动驾驶技术和物联网技术的不断发展，研究内容还将与智能无人农机管控平台集成，逐步实现无人农场农机的智能化任务调度、自动化路径规划以及生产作业的全程管控。