基于频率响应分析的机械液压装置建模方法研究

黄学进，郑文华，余 婷

(中国航发控制系统研究所,江苏 无锡 214063)

0 引言

在航空发动机领域，随着被控对象的控制性能与精度要求越来越高，控制系统也变得愈加复杂。机械液压装置作为控制系统的核心组成部分，对其进行设计、生产、测试、应用、维护的全生命周期管理，能够显著提高航空发动机控制系统生产效率，降低使用维护成本。在全生命周期管理中，其数学模型应用极为广泛，模型精度也极为重要[1-4]。

在发动机运行过程中，不同的机械液压装置功能不一，状态各异，环境差异性较大，其机械结构、控制模式也有诸多不同。针对机械液压装置这类高阶系统，在其性能分析的过程中，采用时域分析法求解十分困难，难以获得其准确的模型与参数。

频域分析法则可以通过图解法对控制系统进行分析，并用于控制器的分析与控制参数的整定。频域特性物理意义明确，对于不同阶次的系统，频域性能指标可以和时域性能指标建立近似的对应关系，既可以考虑系统动态响应，也可以方便地抑制噪声，具备较好的鲁棒性[5-6]。

频域分析法常用于分析和设计控制系统，尤其是线性定常系统[7-8]。它能够根据系统的开环频率特性去判断闭环系统的稳定性，分析系统参数对系统性能的影响，在控制系统的校正设计中应用广泛[9-10]。

频率特性可以应用机理分析法，根据系统的工作原理建立起来，或者采用扫频方法来建立模型，也可以由系统的传递函数、微分方程等数学模型转换过来[11-14]。

本文采用频域分析法，对某机械液压装置进行频域建模，并对模型精度进行验证，用于对此类机械液压装置的全数字仿真和硬件在回路验证，用于控制算法的优化和控制参数的整定，并在机械液压装置全生命周期管理平台中进行应用。

1 频域分析原理

1.1 频率响应原理

用频率特性描述机械液压装置的动态特性时，一般表达如下式所示[15]：

(1)

式中，Y(s)为待辨识对象输出的拉氏变换，U(s)为输入的拉氏变换。复变量G(jw)可以反映出在不同频率的正弦信号作用下，输出信号的稳态分量与输入信号之间的关系。式(1)可以写成如下形式：

Y(jw)=G(jw)U(jw)

(2)

表示对辨识对象的输入一个频率w、幅度为Au、相位为φu的正弦信号：

u(t)=Ausin (wt+φu)

(3)

对于线性系统，对象的稳态输入量y(t)也是同样频率w的正弦信号，但其幅度为Ay、相位为φy：

y(t)=Aysin (wt+φy)

(4)

输出信号的增益与输入信号的增益之比A(w)=Ay/Au随频率而变化，即幅频特性。输出信号的相位与输入信号的相位之差φ(w)=φy-φu也是随频率而变化，即相频特性。辨识对象的动态特性可以完全由这两个量来描述。它们与频率特性G(jw)的关系是：

G(jw)=A(w)e(jφ(w))

(5)

1.2 频率响应实施方法

正弦信号的频率响应为与输入同频率的正弦信号，其幅值和相位的变化量均为频率ω的函数，因此系统的数学模型可以用频率响应实验的方法来确定。

首先要选择输入到对象的正弦信号的幅值，使系统的状态为非饱和。对应的稳态输出信号为一个频率相同但幅值与相位不同的正弦信号，利用稳态段的输入输出信号计算幅值比和相位差来计算频率特性。其幅值比为：

(6)

式中，Ai(w)为输入的正弦信号幅值，A0(w)为稳态输出波形的幅值，w=2πf为信号的角频率。相位差通过获取稳态输入输出波形峰值之间的时间差t来计算：

(7)

在一定范围内改变正弦输入信号的频率，记录下在各个频率处对象输出量的波形信息，得到不同频率下的幅值比和相位差即可作出对象的频率特性曲线图。常用的频率特性曲线有幅相频率特性曲线、对数频率特性曲线和对数幅相特性曲线。由于图对ω采用对数分度，扩展了在实际系统中非常重要的低频段，并且可以根据对数幅频特性曲线和对数相频特性曲线分析辨识对象传递函数中包含哪些典型环节，故而选用对数频率特性曲线表示。从低频段起，将得到的对数频率特性曲线用渐近线分段近似，获得对数幅频渐近线，确定系统传递函数的具体结构。

根据实际被控对象的动态特性，控制带宽为0～10 Hz，因此测试信号的最低频率设置为0.01 Hz，最高频率为10 Hz。

1.3 频响分析仪工作原理

频响分析仪是测量被测系统频率特性的仪器。目前，频响分析仪广泛应用于伺服系统的设计与调试以及自动控制系统科研与测试等领域[17]。

频响分析仪主要由：发生器、分析仪、控制器、运算器以及键盘显示器等组成，其原理框图如图1所示。

图1 频响分析仪原理

由信号发生器产生一个正弦波或方波电激励信号，用于系统测试。两个分析器，它们在系统的两个点上测量对应于激励信号的响应，经过运算器完成数学相关运算后由显示器显示测量结果。

频响分析仪的频率范围实用性广，幅度范围大，幅值精度高，AD分辨率高，能够产生符合机械液压装置要求的激励信号，通过采集反馈并运算获得更加精确的参数[18-19]。

利用频率响应分析，在闭环控制回路中设置求和点，将频率响应分析仪激励信号加入闭环回路。同时在求和点前将闭环信号反馈到频率响应分析仪输入端，供频率响应分析。

在频率测量中，基波的输入、输出关系如下：

系统输入信号X(t)=Asin(ωt)

系统输出信号Y(t)=Rsin(ωt+θ)

为了测量频率响应必须测量R和θ以得到增益和相移，因此输出信号Y(t)可写成：

Y(t)=Rcosθsinωt+Rsinθcosωt=

Psinωt+Qcosωt

式中：

P=Rcosθ=同相分量(实部)

Q=Rsinθ=正交分量(虚部)

θ=tan-1(Q/P)

频响分析仪输出一个Usinωt信号去激励被测系统，响应信号为Y(t)，此信号通过乘法器分别与正弦和余弦相乘，然后送到积分器进行积分，最后显示同相分量和正交分量[20]。其原理如图2所示。

图2 频响分析仪原理

频响分析仪还采用了相关滤波抑除了全部直流分量和高次谐波，只要积分时间足够长，噪声的影响也可忽略不计，保证了在测量过程中抑除各种干扰，从而保证了测量精度。

2 机械液压装置回路模型辨识

2.1 机械液压装置控制原理

本文以某机械液压装置控制回路为研究对象，该机械液压装置的控制由控制单元和机械液压装置协同完成。机械液压装置由计量活门、高速电磁阀、位置传感器等组成。其控制回路原理如图3所示。

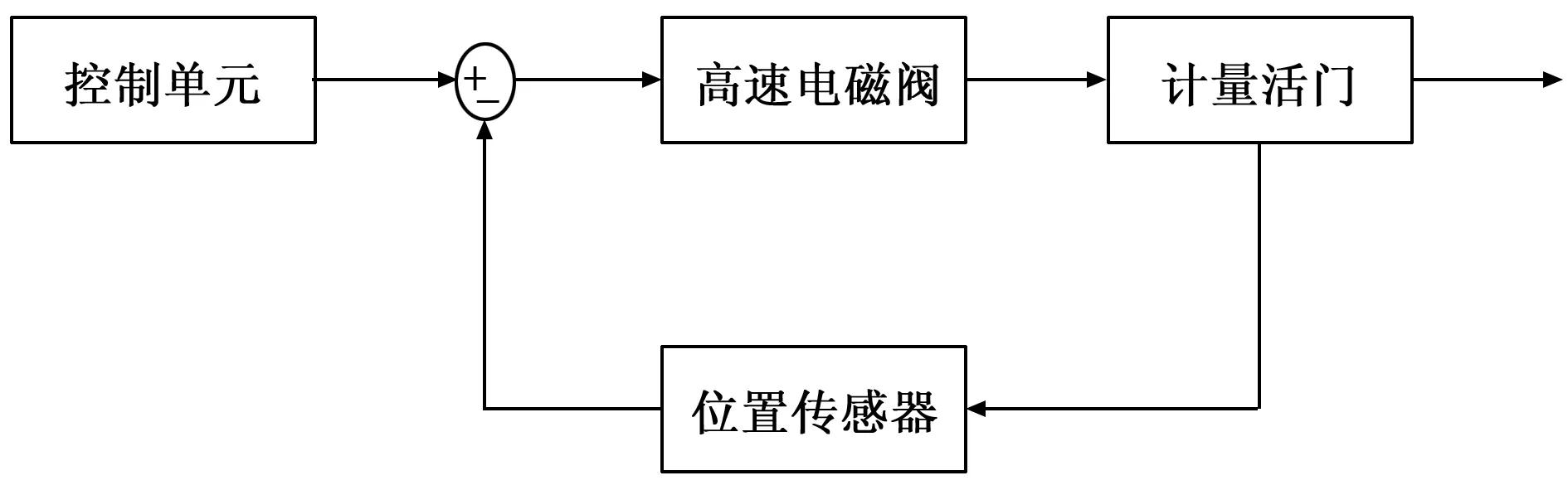
图3 机械液压装置控制回路原理

2.2 机械液压装置控制回路辨识

采用频响分析法进行回路辨识的原理如图4所示，图中忽略了软件滤波功能。

图4 频率响应分析法回路连接示意图

图4中，从B点到A点的传递函数为：

(8)

对单变量系统，各传递函数可以互换位置。当P6=P5时，B点到A点的传递函数可写为：

(9)

因此，根据频率响应分析仪测量的B→A的传递函数T，可求得包括控制单元实现的控制算法C、驱动电路、执行机构、传感器、信号处理电路、A/D转换全过程在内的综合传递函数，即辨识出控制单元输出到控制单元输入之间的机械液压装置回路被控对象的实际传递函数PC。

将控制算法C从上述传递函数中除去，则可得包括驱动电路、执行机构、传感器、信号处理电路、A/D转换全过程在内的综合传递函数P。

为使被控对象容易求解，辨识软件中控制单元采用简单比例控制。

忽略AD转换、采样、软件滤波(5 ms滑动滤波)，P代表(以机械液压装置为例)控制信号→反馈信号的传递函数。

2.3 回路辨识结果

回路的扫频试验中各参数设置如下(Kp=0.1%/Bit)：

表1 控制信号→反馈信号扫频参数设置表

表中不同的反馈信号、转速代表了频率响应分析时选取的不同状态点。△V表示扫频幅值。后续表格中相应数据的意义类似，不再赘述。

在不同参数下的扫频曲线对比伯德图如图5所示。

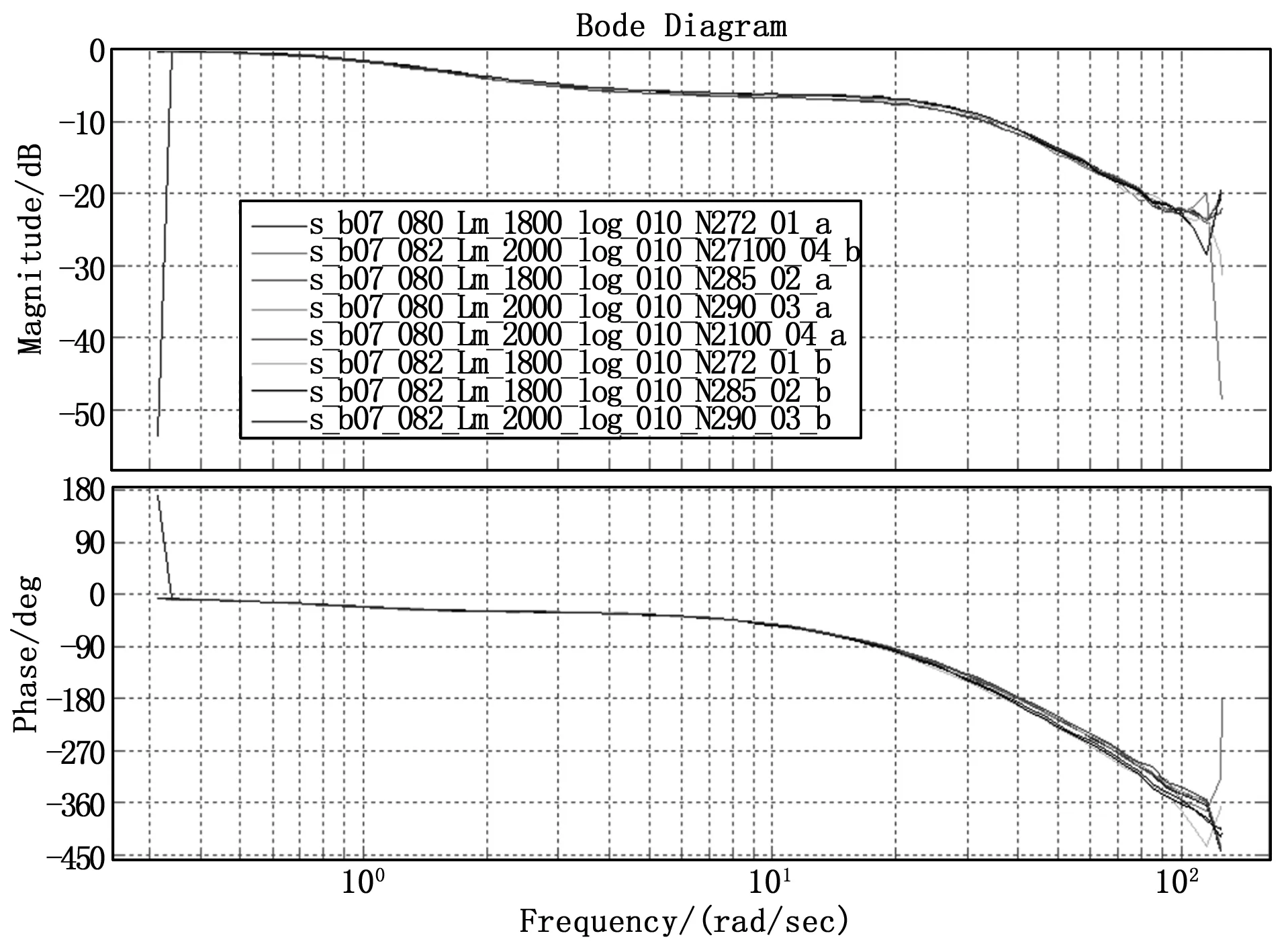
图5 机械液压装置对比伯德图

由图可以看出Δ反馈→反馈信号回路的曲线一致性及重复性较好。为了减小试验数据中误差的影响，对上述几组数据求平均再拟合开环传递函数。

拟合开环传递函数的过程为首先利用试验获得的闭环传递函数求出开环传递函数：Top=Tcl/(1-Tcl)，然后利用Top拟合出开环传递函数。

试验次数中标明“MIN”的表示此组曲线数据的输出响应衰减为最小时拟合出来的开环传递函数，标明“MAX”的表示此组曲线数据的输出响应衰减最大时拟合出来的开环传递函数，标明“Average”的表示对数据求平均后拟合出的开环传递函数。

2.4 HIL与半物理对比验证

由于Kp=0.1%/Bit，故将拟合后的Δ反馈(Bit)→反馈信号(Bit)回路的开环传递函数G(s)再除以Kp即可得控制信号(%)→反馈信号(Bit)回路的开环传递函数G(s)/Kp。具体开环传递函数见表2～3，其特性为带纯滞后的一阶超前滞后环节与纯积分环节串联。

表2 Δ反馈→反馈信号回路辨识结果

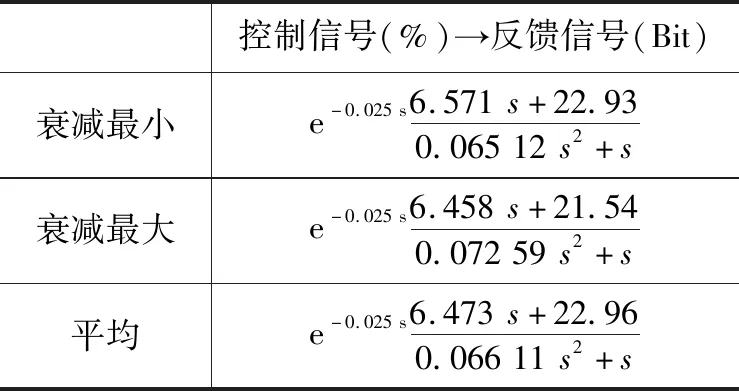
表3 控制信号→反馈信号回路辨识结果

衰减最小时的拟合对比曲线如图6所示，其中左列为闭环传递函数拟合对比，右列为开环传递函数拟合对比。

图6 反馈信号在衰减最小时的传递函数拟合

衰减最大时的拟合曲线如图7所示，其中左列为闭环传递函数拟合对比，右列为开环传递函数拟合对比。

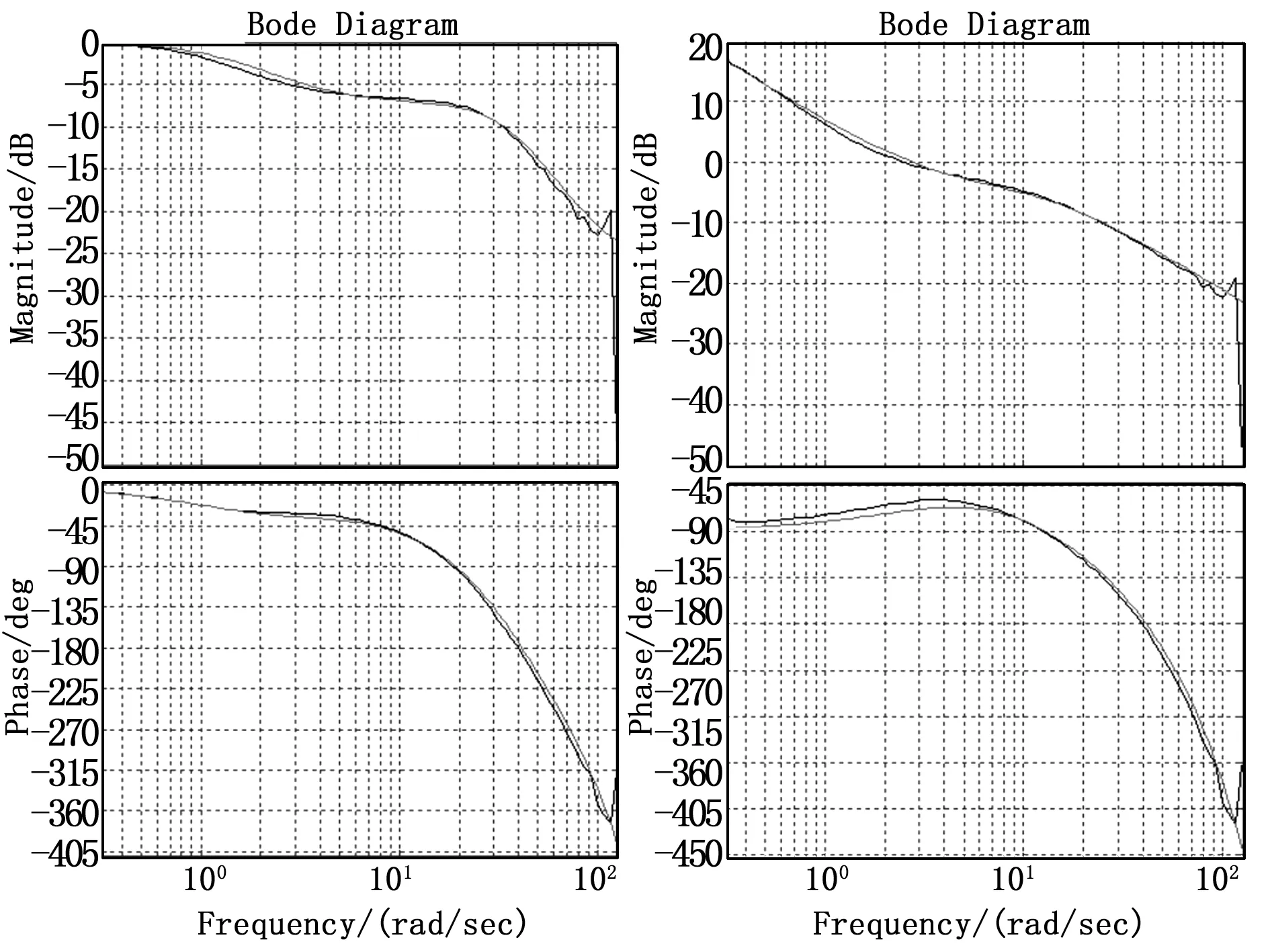
图7 反馈信号在衰减最大时的传递函数拟合

求平均后的拟合曲线如图8所示，其中左列为闭环传递函数拟合对比，右列为开环传递函数拟合对比。

图8 反馈信号Average

从最大、最小及平均传递函数拟合结果可见，反馈信号回路特性具有较好的一致性。从拟合结果对比图可见，拟合特性较为准确。

利用辨识出的机械液压装置回路模型，按图9建立机械液压装置回路仿真模型：

图9 反馈信号机械液压装置回路框图

对机械液压装置全行程内进行HIL和半物理试验数据对比验证，归一化对比数据如图10～12所示。

图10 全行程内阶跃控制对比

图11 全行程内阶跃控制误差

图12 全行程内斜坡控制对比

在该机械液压装置的主要特征点进行阶跃响应，阶跃量为1 800→1 900 bit，并与实际被控对象阶段响应对比，该模型在Simulink中的控制结果如图13所示，真实执行机构控制效果如图14所示。

图13 反馈信号-模型阶跃响应

图14 反馈信号-实际阶跃响应

具体参数数据如表 4所示。

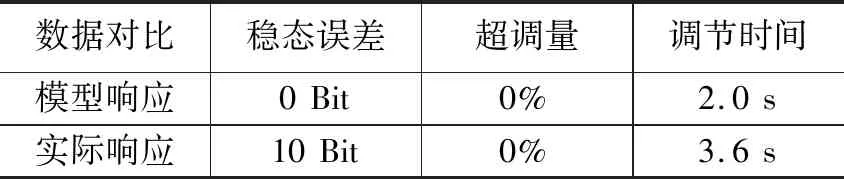
表4 控制信号→反馈信号仿真结果

由曲线及参数数据表可见辨识所得的模型与对应调节器实际试验响应差别不大，因此其模型辨识精度可认为是满足所需要求的。

3 频响稳定性分析

进行控制信号→反馈信号回路的稳定性扫频试验，由试验数据获得的曲线对比图如图17所示。

图15 反馈信号稳定性对比伯德图

由曲线图可以得到增益裕度与相位裕度如表 5所示。

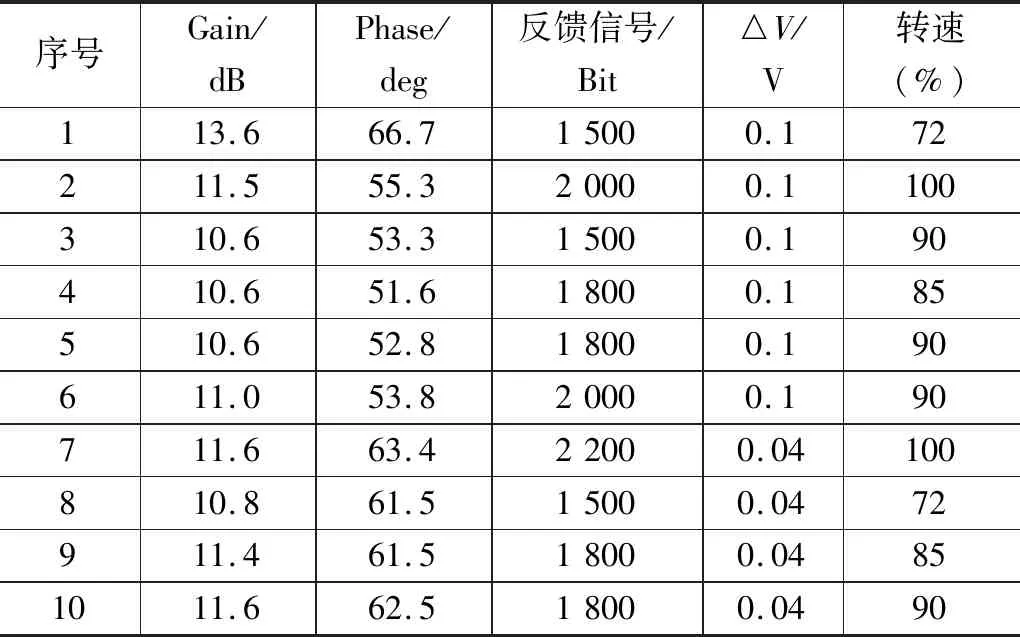
表5 反馈信号回路扫频试验数据

通过反馈信号回路扫频试验数据可以得出，幅频裕度大于6 dB，相位裕度大于45°。幅频、相位裕度均满足设计要求。

4 构建机械液压装置全生命周期管理平台

机械液压装置全生命周期管理平台是以信息化管理为核心，通过技术手段将机械液压装置全生命周期的相关数据整合在统一的信息平台上，对其设计、生产、测试、应用、维护状态下同一产品的状态进行有效管控，对机械液压装置的设计形成指导作用，提高产品设计效率，降低测试维护成本，并实现产品故障预测。

机械液压装置全生命周期管理平台总体架构如图16所示。

图16 全生命周期管理平台架构

管理平台监控界面如图17所示。

图17 管理平台状态监控界面

在机械液压装置全生命周期管理平台中，主要收集以下几个方面的数据：

设计研发阶段，由CATIA、SolidWorks等三维设计软件设计的结构数据以及结构仿真数据，以及Matlab、AMESIM等软件的仿真数据；

在生产制造阶段，由机械液压装置综合测控设备产生的硬件在回路仿真数据；

在调整测试阶段，由机械液压装置综合测控设备产生的半物理试验数据；

在装机应用过程中由电子控制器记录的实时机载数据；

在维护保障阶段，由地面检测设备产生的维护测试数据。

在调整测试阶段，使用频域分析方法构建机械液压装置的数学模型，并用于全数字仿真和硬件在回路仿真，并在管理平台中将模型仿真数据与实时机载数据、维护测试数据进行对比，实现对机械液压装置的实时性能监控，并指导对该机械液压装置的维修保障与寿命预测。

5 结束语

通过对机械液压装置控制回路进行频率响应试验，辨识出控制系统中执行机构被控对象的传递函数，并通过全数字模型仿真与试验数据对比，一定程度上验证了模型的准确性。本文证明了频域建模的有效性，为机械液压装置控制系统全数字仿真与硬件在回路仿真提供了较为精确的模型，并将其应用于机械液压装置全生命周期管理平台。