利用协同反演方法反演地震序列滑动分布

王乐洋 , 谷旺旺, 孙龙翔

东华理工大学测绘工程学院， 南昌 330013

0 引言

大地测量反演是研究地球科学的关键手段，通常采用大地测量数据反演断层面滑动的大小与分布、应力分布以及地震机制等(Xu et al., 2017; Wang et al., 2018b; Wang and Gu, 2020).随着大地测量观测技术的不断发展以及观测手段的增加，越来越多的观测资料用于滑动分布反演中，其中GPS和InSAR以其高时间和空间分辨率成为滑动分布反演的重要数据.随着数据种类的增加，联合不同数据进行反演成为研究的方向.由于大地测量反演问题通常是病态的，导致不同数据反演结果存在差异；显而易见，能够同时解释多类数据的模型更有说服力.由于不同类数据的优势与劣势各不相同，如何扬长避短弥补不同数据之间的劣势，发挥多类数据的优势成为研究的热点.其中，联合反演方法有效将多类数据进行融合，统一反演最优模型.而联合反演应用的关键问题在于相对权比的确定，它体现了各类数据在联合反演中的贡献程度.目前已有大量学者对此进行相关研究，其中Xu等(2009)总结目前较为常见的定权方法：将相对权比作为未知参数统一求解；根据先验信息确定；将不同类数据视为等权处理；采用赫尔默特方差分量估计法(Helmert Variance Component Estimation, HVCE)确定.Xu等(2009)表明HVCE法能够得到合理的相对权比.Xu等(2006)研究了病态问题中方差分量估计法的适用性，提出对参数的残差进行偏差改正的方差分量估计法.Xu(2009)研究了利用正则化方法求解的参数是有偏的，通过偏差改正以获得更精确的验后方差.王乐洋等(2012)提出了确定联合反演相对权比的两步法，并针对不同目标函数对相对权比的影响进行了讨论.Huang等(2013)采用方差缩减法确定联合反演的相对权比和正则化参数.Wang等(2018a)采用U曲线法确定正则化参数，判别函数最小化法确定相对权比，实验结果表明该方法能够在均方误差意义下优于方差分量估计法.许才军等(2016)提出采用方差分量估计法同时确定相对权比和正则化参数，拓展了方差分量估计法的应用范围.Goldberg等(2020)根据不同相对权比下GPS与InSAR的均方根误差确定两类数据的相对权比.以上方法均将不同观测数据联合到一个模型下进行求解，通过权比控制不同数据反演所占权重.考虑到相对权比的确定对反演的结果会产生不同的影响，而相对权比的确定并没有一个统一标准.在地震序列反演中，由于部分数据为单次地震获取的同震形变场，而其他数据包含了整个地震序列的同震形变，这将导致这部分数据无法用于单次地震的反演.Li等(2020)表明采用整体形变数据进行反演会造成反演结果存在折衷，并不能反演实际滑动分布.针对此问题，Goldberg等(2020)根据地质信息勘测到单次地震的破裂情况，利用多种数据进行联合反演，并根据数据的均方根误差确定相对权比.Wang等(2020)通过单次地震数据作为先验信息，通过迭代的方式将包含整个地震序列的同震形变进行分离，从而反演出单次地震的滑动分布.以上方法均将不同数据联合到同一个方程中进行求解，由于InSAR数据为两次地震共同产生的形变，为了得到分离的形变数据，考虑采用协同反演方法进行反演.

协同反演方法在地球物理联合反演中具有广泛的应用，Lines等(1988)首次提出协同反演方法，并利用地表地震数据、声波测井、地表重力数据和井眼重力仪数据进行了反演.随后大量学者对此进行了深入研究.Anderson等(1998)采用顺序联合反演法利用地震和重力资料反演速度和密度参数，为深度偏移成像提供准确的速度模型.Paasche等(2012)扩展了基于模糊C-means聚类分析和单一数据集反演算法的区域协同反演方法，用于部分位于同一模型区域的数据的协同反演.McMillan和Oldenburg(2014)采用协同反演方法反演了具有边界约束的电磁数据，得到了具有改进分辨率的一致的3D电阻率模型.Takam-Takougang等(2015)提出了一种协同反演方法，利用地震和大地电磁数据联合反演声阻抗.Le等(2016)测试了不同联合反演策略，验证了所提出的协同反演方法与其他反演手段一致的电导率分布.认为在并行计算的帮助下，地震的大地电磁数据的协同反演可以实现自动化.Moorkamp(2017)讨论了联合反演和约束反演方法的基本原理，并讨论了联合反演方法中不同耦合方法的特点.Gonçalves和Leite(2019)提出了一种利用复杂地质结构叠后地震反射和重力数据偏移2D协同反演方法，通过减少变量数量提高了算法的计算效率.Singh等(2019)提出了一种利用模糊C-means聚类协同反演方法反演出更可靠的电阻率和密度模型.

协同反演方法在地质勘探中应用较多，但并没有应用于滑动分布反演中.在大地测量反演中，联合反演均采用同步联合反演，即将多类数据联合到一个模型中进行解算，采用不同的相对权比区分每类数据的权重影响；而并未考虑到协同反演方法，即顺序联合反演，利用单一类型数据进行反演，将反演结果作为另一类数据的先验信息进行反演，如此反复迭代.由于顺序联合反演方法具有无需考虑相对权比的优势，本文将顺序联合反演方法引入到大地测量滑动分布反演中，一方面可以有效地获得地震序列的滑动分布情况，另一方面避免了相对权比确定问题.

1 协同反演

1.1 地震同震滑动分布反演基本原理

在同震滑动分布反演中，地表同震形变位移与断层滑动之间可以通过线性函数连接，其表达式为

d=Gm，

(1)

其中，d表示观测向量(如InSAR视线向位移、GPS位移场等)；G表示格林函数矩阵，利用均匀弹性半空间矩形位错模型(Okada, 1985)确定；m为滑动参数.

利用最小二乘法对式(1)进行求解时，由于格林函数矩阵的复共线性，造成了求解过程中法矩阵病态，通常对滑动参数添加一定的平滑约束，使系数矩阵满秩，且能够避免滑动解出现非物理因素的震荡.一般采用拉普拉斯二阶平滑算子对断层单元进行平滑约束，可表示为

Hm=0，

(2)

联合式(1)和式(2)，得到滑动分布反演公式为

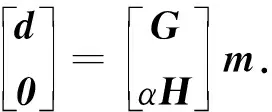
(3)

利用最小二乘法求解式(3)，即可获得滑动参数解.滑动参数解可表示为

m=(GTPG+α2HTH)-1GTPd，

(4)

其中，P为观测数据的权阵，α为平滑因子，文中采用方差分量估计法进行确定.

1.2 方差分量估计法基本原理

根据式(1)和(2)，得到GPS和InSAR数据联合反演滑动分布公式(Xu et al., 2017; Wang et al., 2018a)为

(5)

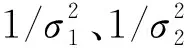
利用方差分量估计法对式(5)进行迭代求解，可以得到GPS和InSAR数据的相对权比和平滑因子，当仅为GPS或者InSAR数据时，采用方差分量估计法可以用于确定平滑因子.

1.3 协同反演方法基本原理

利用多类数据进行协同反演时，首先利用一类数据进行滑动分布反演，将反演的滑动参数作为另一类数据反演的先验信息进行约束.假设本文仅考虑利用GPS和InSAR数据进行协同反演.由于在协同反演中进行了迭代运算，故利用何种数据首先进行滑动分布反演对结果并没有影响.由于本文考虑将协同反演方法应用于地震序列中，假设一个地震序列包含了两次地震，第一次地震称为前震，第二次地震为主震.由于GPS数据的时间分辨率非常高，能够得到单次地震的同震形变，故本文首先分别利用两次GPS数据进行滑动分布反演，得到滑动分布反演公式为

(6)

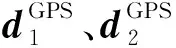
利用最小二乘法求解式(6)，得到利用GPS数据反演两次地震的滑动分布解m1、m2，其中平滑因子采用方差分量估计法确定.

根据式(6)可以得到前震和主震的滑动分布，将GPS数据反演结果作为InSAR数据反演的先验信息，可以得到InSAR数据的滑动分布反演公式为：

(7)

利用最小二乘法求解式(7)，得到利用GPS数据反演两次地震的滑动分布解m′1、m′2.

根据式(7)得到InSAR数据约束下的滑动分布，将反演结果作为下一次GPS数据反演的先验信息，可以得到附有先验信息的滑动分布反演公式为

(8)

利用式(7)和(8)进行迭代，最终能够得到拟合两类数据的滑动模型.

本文给出利用GPS和InSAR数据进行协同反演的迭代步骤：

(1)分别利用前震和主震GPS数据进行滑动分布反演，反演公式如式(6)，利用方差分量估计法确定正则化参数，采用最小二乘法求解滑动分布，得到前震与主震的滑动分布分别为m1和m2；

(2)将断层滑动分布m1和m2作为先验信息，采用最小二乘法求解式(7)，得到InSAR数据约束下反演的滑动分布分别为m′1和m′2；

(3)将步骤(2)中求得的滑动分布m′1和m′2作为先验信息，根据式(8)利用GPS数据反演前震和主震滑动分布，得到两次地震的滑动分布为m″1和m″2；

(4)计算步骤(2)和步骤(3)分别求得的滑动分布解m′1和m′2与m″1和m″2的拟合残差，若残差小于阈值，迭代终止；否则重复步骤(2)—(4).

协同反演迭代流程图如图1所示.由于设置不同的阈值，导致迭代的结果并不相同，当阈值设置较小时，反演得到的形变值残差较小，但这伴随着反演的滑动分布可能出现非物理震荡，基于此我们根据残差与平滑度之间的折衷选取阈值的大小.

图1 协同反演迭代流程图Fig.1 Iterative flow chart of cooperation inversion method

2 模拟实验

为了验证协同反演方法在地震序列中的可行性，本文做了以下模拟实验.在模拟实验中，模拟了一对正交共轭断层，其断层面几何参数如表1所示，断层面分布如图2所示.模拟两次地震累计产生的形变量，并施加观测误差N～(0,12cm2),图3为InSAR数据降采样后的数据分布图.同时模拟了两次地震GPS3方向形变数据如图4和图5所示，并给形变点施加观测误差，其中水平方向施加N～(0,32mm2)的观测误差，垂直方向施加N～(0,52mm2)的观测误差.在模拟实验中，由于加入的误差是标准正态分布的，且误差较小，故我们设置了较小的阈值进行迭代，阈值为10-5m.

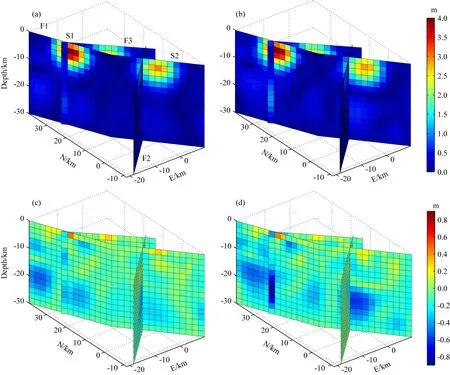
图2 模拟实验的滑移分布结果与残差分布(a) 联合反演方法反演的滑移分布结果； (b) 协同反演方法反演的滑移分布结果； (c) 联合反演方法的残差分布； (d) 协同反演方法的残差分布.Fig.2 The results of simulated slip distribution inversion and their residuals(a) The results of slip distribution inverted by the joint inversion method; (b) The results of slip distribution inverted by the cooperation inversion method; (c) The results of residuals by the joint inversion method; (d) The results of residuals by the cooperation inversion method.

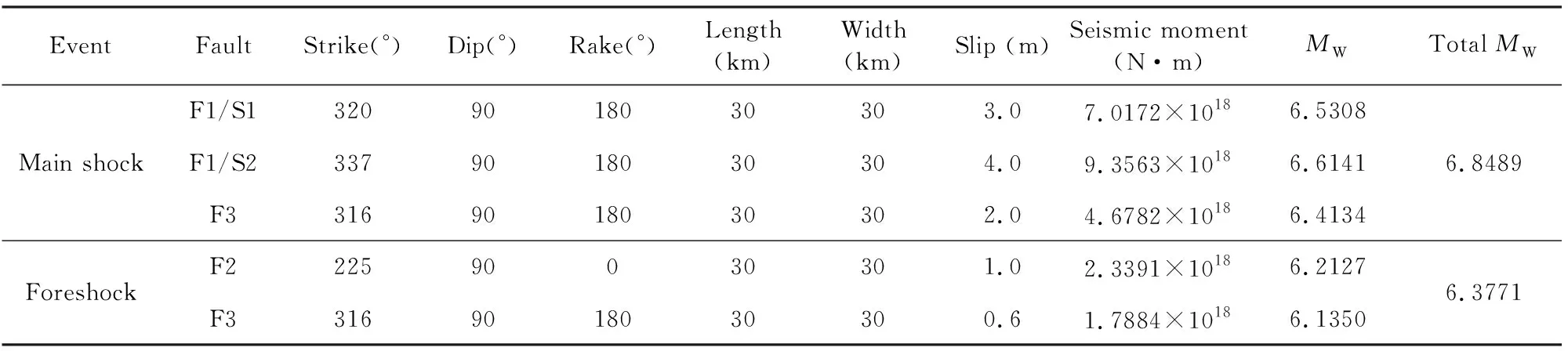
表1 模拟地震震源参数Table 1 The real source parameters of the simulated earthquake

在模拟实验中，分别采用联合反演和协同反演方法进行滑动分布反演，其中联合反演中利用方差分量估计法确定的相对权比为1∶ 0.9697∶ 1.6039∶0.0004，在协同反演中正则化参数采用方差分量估计法进行确定，正则化参数分别为0.0583和0.0136.图2为两种方法反演的滑动分布及其残差分布，其中(a)和(b)分别为联合反演和协同反演方法反演的滑动分布结果，(c)和(d)分别为两种方法对应的残差分布结果.在模拟实验中，利用联合反演和协同反演方法得到的地震滑动分布各参数结果见表2.

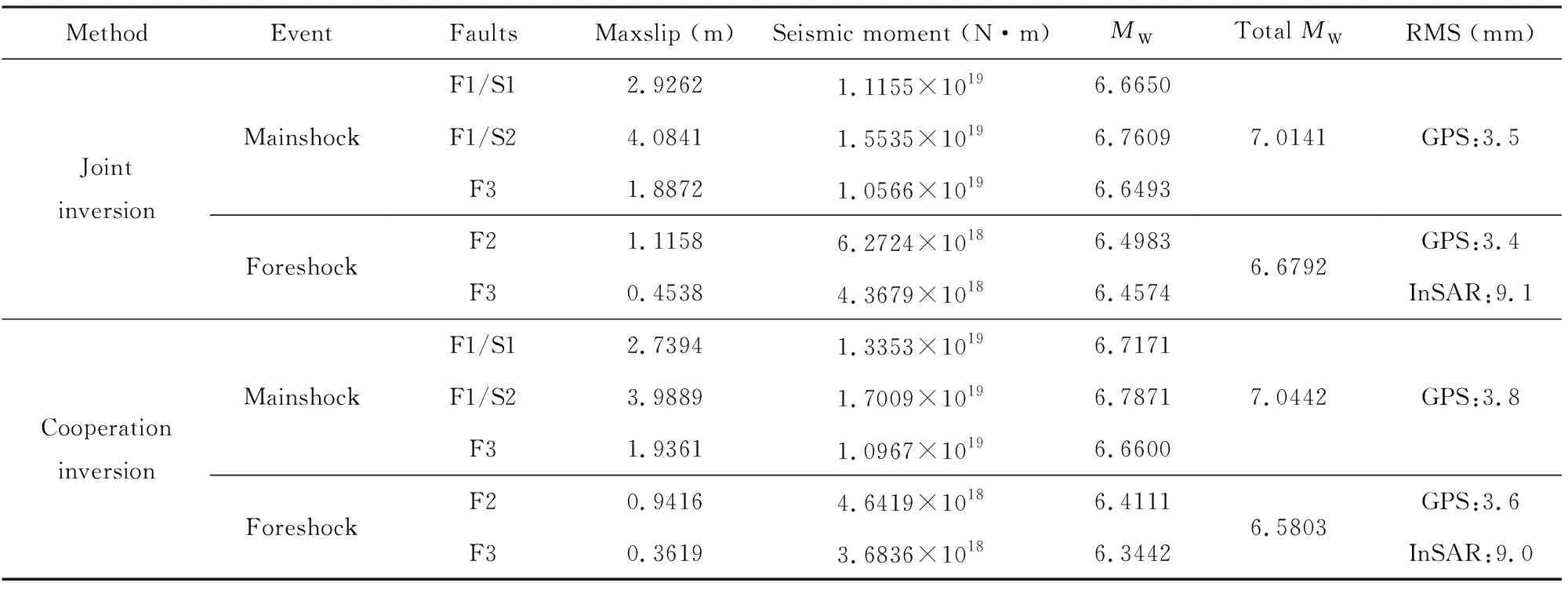
表2 模拟实验反演地震滑动分布结果Table 2 The results of slip distribution inversion in simulation experiment

根据表2反演结果可以看出，两种方法均能很好反演出模拟的滑动分布，且数据的拟合残差仅有微小差别，其中采用方差分量估计法反演结果正演的GPS数据的拟合残差分别为3.5 mm和3.4 mm，InSAR数据的拟合残差为9.1 mm；而采用协同反演方法反演结果正演的GPS数据的拟合残差分别为3.8 mm和3.6 mm，InSAR数据的拟合残差为9.0 mm.但两种方法反演结果略有不同，其中采用方差分量估计法确定相对权比的联合反演方法反演出的断层S2及F2的最大滑动量超过了模拟设置的滑动量，而其他断层的最大滑动量与模拟值相比较小，这很有可能是反演不同的断层之间的滑动存在一定的折中，这与Li等(2020)反演结果相一致.由于模拟实验中，模拟的观测数据所加入的随机误差较小，反演的结果与模拟值相差不大.对于协同反演而言，各个断层的滑动量与模拟值较为接近，仅前震F3断层反演的滑动量较小，主要是模拟中F3断层的滑动位置处于断层较深处，且其滑动量较小，故难以反演出其真实滑动大小.总体而言，两种方法的反演结果较为一致，且其数据的拟合残差较小，仅有微小差异，故能够验证协同反演方法应用于滑动分布反演的有效性.

图2展示了利用方差分量估计法和协同反演方法反演的主震与前震的滑动分布以及两种反演结果与模拟滑动之间的残差分布.从图中可以看出整个地震产生了多个断层的滑动，故设置了不用的断层来反演每个断层的滑动情况；对比两种方法的反演结果，主要滑动区的滑动保持一致，仅在非滑动区存在较小的差异，这是平滑约束所引入的，无法通过本文方法消除；且设置的最大滑动量和反演的滑动量之间较一致，这也与模拟数据所加入的误差有关，模拟数据的误差为正态分布且误差量级较小，所以通过本文两种方法能够有效地反演出每个断层上的滑动，且整体误差较小，故通过模拟实验能够验证协同反演的有效性.从图中两种方法的残差图可以看出，在模拟滑动区域，两种方法都能够较好地反演出实际滑动，仅在S1断层的地表处显示出部分滑动低于实际滑动，这主要是平滑约束造成的.而在断层的深处，两种方法都出现了部分伪滑移，主要是因为本文设置的断层相比于实际滑动区域较大.

图3展示了两种方法反演的滑动分布模型正演的InSAR形变场以及模拟形变.对比前两列，两种方法反演的形变场与模拟形变场保持较好的一致性，最后一列为两种方法的残差图，从残差的形变尺度上可以看出，最大形变误差在3 cm以内，表明了两种反演方法的精度是非常高的.

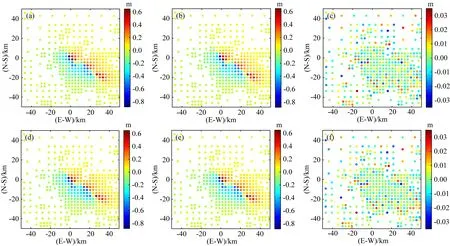
图3 InSAR观测形变值与模拟形变值对比及残差图(a)和(d) 表示InSAR观测数据； (b)和(d) 分别为采用联合反演和协同反演方法得到的模拟值； (c)和(f) 分别表示两种方法反演的残差分布.Fig.3 The observed InSAR displacements, the modeled displacements and their residuals(a,d) represent InSAR displacements, respectively; (b,d) The modeled displacements obtained by the joint inversion and the cooperation inversion method, respectively; (c,f) represent the residuals obtained by the joint inversion and the cooperation inversion method, respectively.

图4展示了前震GPS形变图的模拟形变量和采用方差分量估计法和协同反演方法正演的GPS形变场；图5展示了主震GPS形变图的模拟形变量和两种方法正演的GPS形变场；从图4和图5的结果可以看出，本文两种反演的模型的正演形变场与模拟形变场非常吻合，由于模拟实验中所加入的误差是正态分布且误差较小，所以反演模型与模拟值较为一致.

图4 前震GPS观测形变值与模拟形变值及残差图(a) 蓝色箭头和红色箭头分别表示观测的和联合反演模拟的GPS水平位移； (b) 蓝色箭头表示联合反演模拟的GPS水平位移的残差； (c) 蓝色箭头和红色箭头分别表示观测的和协同反演模拟的GPS水平位移； (d) 蓝色箭头表示协同反演模拟的GPS水平位移的残差； (a)和(c) 中每个测站的彩色圆圈表示测得的(外圈)和预测的(内圈)GPS垂直位移； (b)和(d)中每个测站的彩色圆圈表示垂直形变的残差.Fig.4 The foreshock GPS observation displacements, the modeled displacements and their residuals(a) The results with blue and red arrows represent the observed and simulated GPS horizontal displacements by joint inversion method, respectively; (b) The results with the blue arrow represent the residuals of the GPS horizontal displacements; (c) The results with the blue and red arrow represent the observed and simulated GPS horizontal displacements of the cooperation inversion method, respectively; (d) The results with the blue arrow represent the residuals of the GPS horizontal displacements; The colored circles at each station in (a) and (c) denotes measured (outer circle) and predicted (inner circle) GPS vertical displacements. The colored circles at each station in (b) and (d) denote the residuals of vertical displacements.

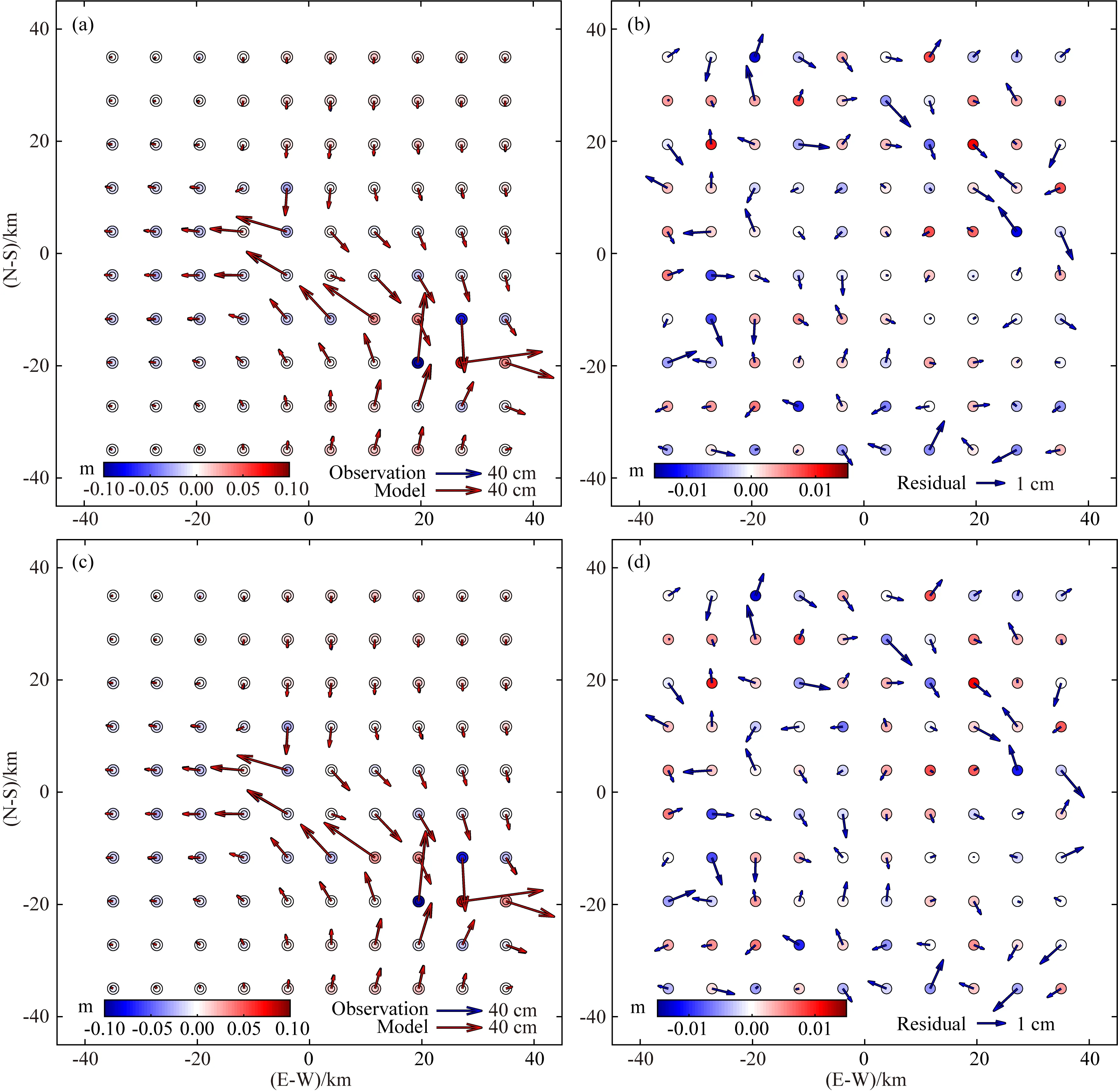
图5 主震GPS观测形变值与模拟形变值及残差图(a) 蓝色箭头和红色箭头分别表示观测的和联合反演模拟的GPS水平位移； (b) 蓝色箭头表示联合反演模拟的GPS水平位移的残差； (c) 蓝色箭头和红色箭头分别表示观测的和协同反演模拟的GPS水平位移； (d) 蓝色箭头表示协同反演模拟的GPS水平位移的残差； (a)和(c)中每个测站的彩色圆圈表示测得的(外圈)和预测的(内圈)GPS垂直位移； (b)和(d)中每个测站的彩色圆圈表示垂直形变的残差.Fig.5 The main shock GPS observation displacements, the modeled displacements and their residuals(a) The results with the blue and red arrow represent the observed and simulated horizontal GPS displacements by joint inversion method, respectively; (b) The results with the blue arrow represent the residuals of the GPS horizontal displacements; (c) The results with the blue and red arrow are the observed and simulated GPS horizontal displacement by cooperation inversion method, respectively; (d) The blue arrow represents the residuals of the horizontal GPS displacements; The colored circles at each station in (a) and (c) denote the measured (outer circle) and predicted (inner circle) GPS vertical displacements; The colored circles at each station in (b) and (d) denote the residual of vertical displacements.

综上所述，采用协同反演方法能够有效地反演出多断层序列地震的滑动分布，且反演精度较高，能够应用于地震序列滑动分布反演研究中.

3 Ridgecrest地震序列

2019年7月4日，加利福尼亚州当地时间17时33分，在加州东部西尔斯谷西南发生MW6.4地震(35.705°N，117.504°W)，在此之后发生了一系列的余震，34 h后发生了MW7.1地震(35.770°N，117.599°W).在Ridgecrest地震序列中，MW6.4地震视为前震，MW7.1地震为主震.该地震序列被大量大地测量数据记录到，为研究该地震序列提供了数据支持.本文从Li等(2020)中获取Ridgecrest地震序列76个GPS点位形变数据，其中前震与主震的形变被单独记录到；从Xu等(2020)中获取Ridgecrest地震序列T65升轨数据1908个，T66升轨数据1976个.根据已有文献公布的断层参数信息(Li et al., 2020; Wang et al., 2020)，我们设置了部分断层参数如表3所示，根据断层参数构建断层面，将断层面均匀剖分成2 km×2 km的矩形单元，并利用协同反演方法反演Ridgecrest地震序列滑动分布，其中正则化参数采用方差分量估计确定，分别为0.0761和0.0339.根据图6拟合残差和平滑度之间的折中曲线，我们得到阈值大小为0.251 m.

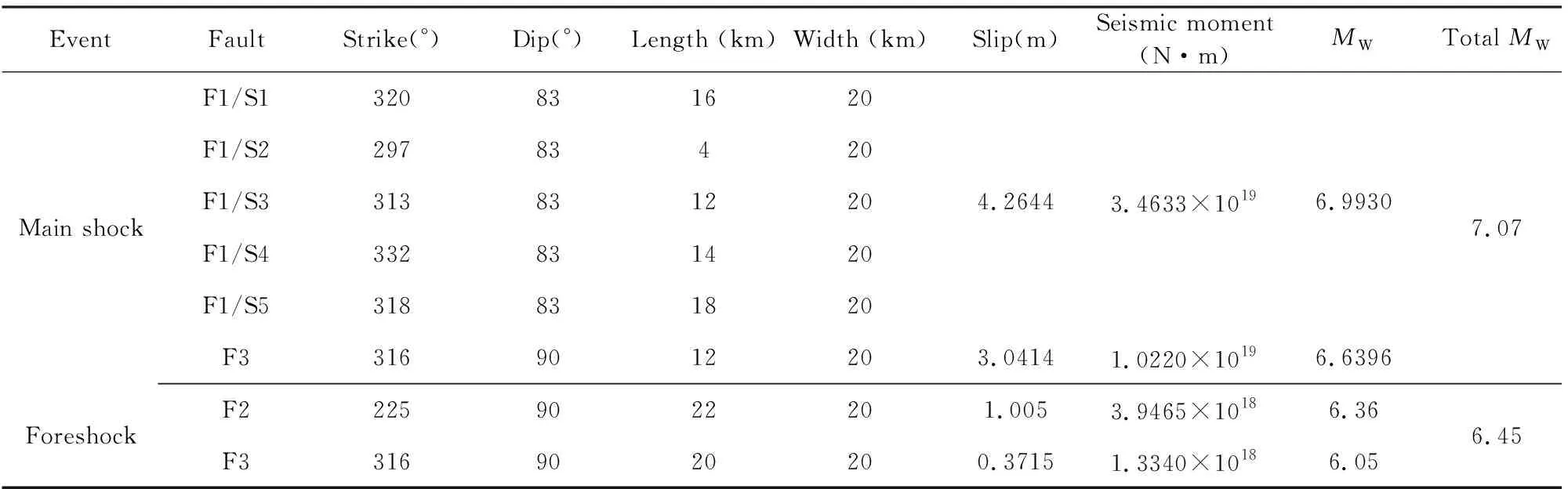
表3 Ridgecrest地震序列的滑动分布参数Table 3 Fault geometry and source parameters of the Ridgecrest earthquake sequence

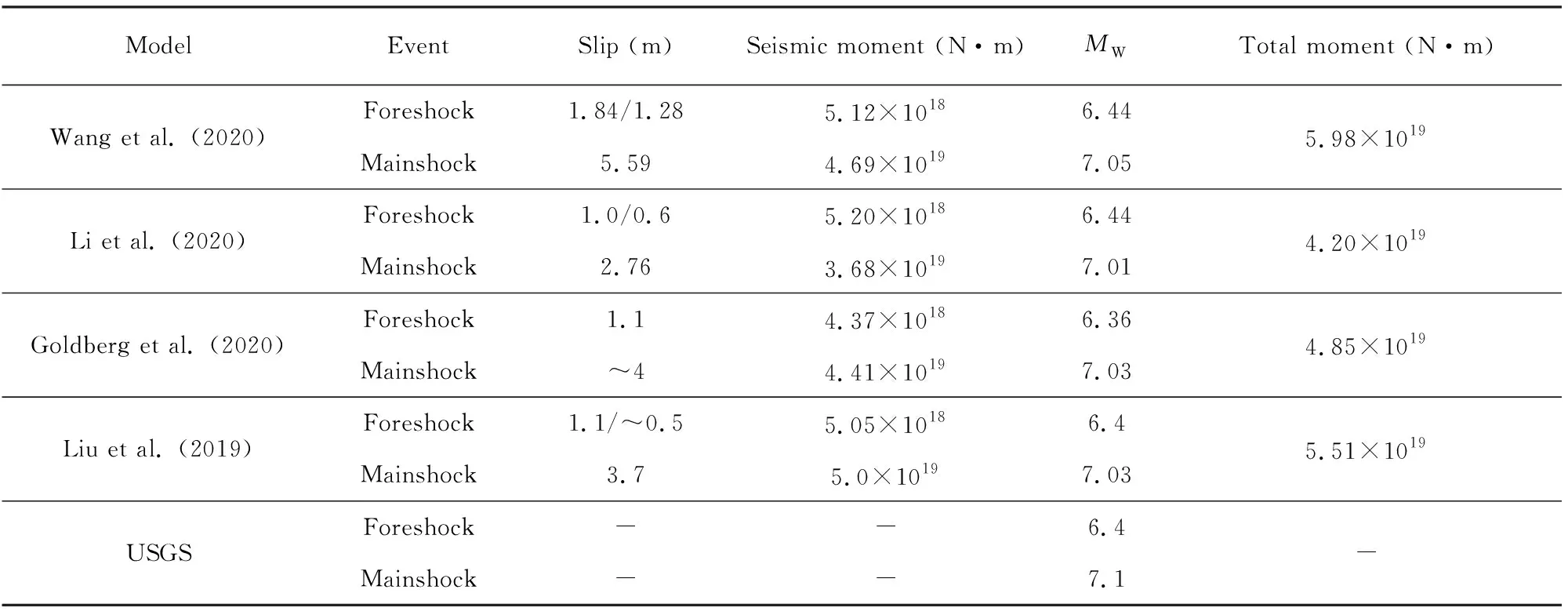
表4 Ridgecrest地震序列主震与前震的滑动分布参数Table 4 The slip parameters of the main shock and foreshock of the Ridgecrest earthquake sequence

反演的滑动分布模型与GPS观测数据拟合较好，其中MW6.4前震GPS数据的水平和垂直方向的拟合残差分别为1.7 mm和6.2 mm；MW7.1主震GPS数据的水平和垂直方向的拟合残差分别为5.7 mm和10.2 mm.图8、9分别展示了前震和主震GPS观测数据与反演模型的正演形变.对于InSAR数据来说，拟合残差较大，尤其在断层线附近，误差高达数十厘米，Li等(2020)表明这些误差的来源可能是模型中表面破裂轨迹的简化、卫星轨道误差、大气延迟和非弹性形变等.图10展示了T065和T066轨道的InSAR形变、反演模型的正演形变以及残差大小.根据反演的滑动模型，主震破裂了断层F1和F3，且F1断层的破裂几乎是纯右旋走滑的，F3断层以右旋走滑为主伴有少量的倾滑.F1断层出现两个主滑动区，其中最大滑动量达到4.26 m.主震破裂高滑动区在地下10 km以上区域，随着深度的增加，滑动逐渐减少.根据本文反演的滑动分布模型，计算出MW7.1主震释放的地震矩为4.49×1019N·m，假设剪切模量为30 GPa，对应于MW7.07，与USGS公布结果较为一致.MW6.4前震破裂了F2和F3断层，且这两个断层具有共轭断层结构的特征，两条断层几乎相互垂直.MW6.4前震的滑动分布如图7所示，主要破裂发生在F2断层，表现为几乎纯左旋走滑特征，其最大滑动量达到1 m，而F3断层对应滑动较小.针对F3断层，MW6.4主震破裂区域离F2断层更近，且破裂深度更深.前震反演的滑动分布模型对应总的地震矩为5.28×1018N·m，对应于MW6.45，略高于USGS给出的结果.Li等(2020)在利用GPS数据进行单独反演时，反演的F2断层滑动量较小，在进行联合反演时F2断层上的滑动量有所提高.而联合反演后F3断层的滑动为两次地震的叠加，其最大滑动量达到～3.95 m，相较于本文结果来说偏大.总体而言，Li等(2020)在仅利用GPS数据进行反演时，由于GPS数据大多分布在远场，约束力不足，其反演结果较为平滑；而加入InSAR数据后，模型得到很好的约束，模型反演的最大滑动量达到～5.5m，累积释放地震矩为4.93×1019，约为MW7.1.Wang等(2020)利用迭代的方式分离了主震与前震的InSAR形变场，并联合GPS数据反演了前震与主震的滑动分布.滑动分布结果显示，F2断层最大滑动量达到2 m，F1断层最大滑动量达到1 m，释放地震矩为5.12×1018，约为MW6.44.对于MW7.1主震，本文滑动分布结果与Wang等(2020)较为相似，存在两个较大滑动区域，最大滑动量达到～5m，略大于本文结果.Goldberg等(2020)提出了一种新的运动学滑动分布反演方法，有效地反演出两次地震的滑动分布情况，并分析了两次地震之间的静、动态库伦应力触发关系.Goldberg等(2020)反演结果表明，MW6.4前震最大滑动量达到～1 m，释放地震矩4.37×1018，约为MW6.36；MW7.1主震最大滑动量达到～4 m，释放地震矩4.41×1019，约为MW7.03.Liu等(2019)联合大地测量和地震波数据反演了2019 Ridgecrest地震序列，其反演结果显示MW6.4前震最大滑动量达到1.1 m，释放地震矩5.05×1018，约为MW6.4；MW7.1主震最大滑动量达到3.7 m，释放地震矩5.0×1019，约为MW7.03.以上文献采用不同的观测数据以及不同的方法对2019 Ridgecrest地震序列进行了同震滑动分布反演，虽然滑动分布存在差异，但其最大破裂区域较为一致；尽管不同学者设置了不同的断层数据进行反演，最终反演矩震级与USGS公布结果较为一致.

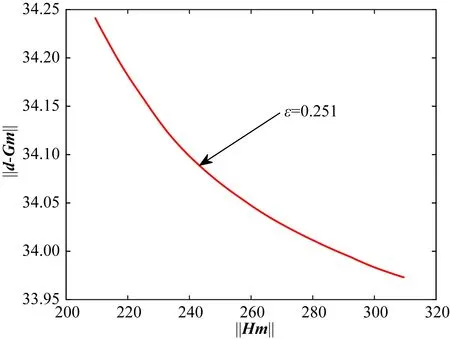
图6 确定迭代阈值的折中曲线图Fig.6 Graph of compromise curve for determining iteration threshold

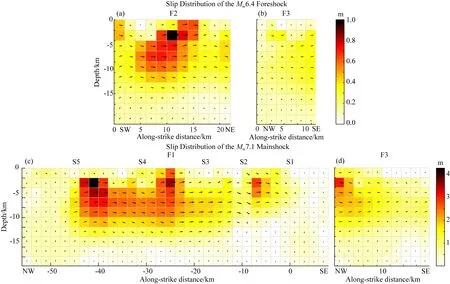
图7 MW6.4前震和MW7.1主震滑动分布结果(a)和(b)分别表示MW6.4前震F2和F3断层的滑移分布； (c)和(d)分别表示MW7.1主震F1和F3断层的滑移分布.Fig.7 The slip distribution of the MW6.4 foreshock and the MW7.1 main shock(a) and (b) represent the slip distribution of faults F2 and F3 for the MW6.4 foreshock, respectively; (c) and (d) represent the slip distribution of the F1 and F3 faults of the MW7.1 main shock, respectively.

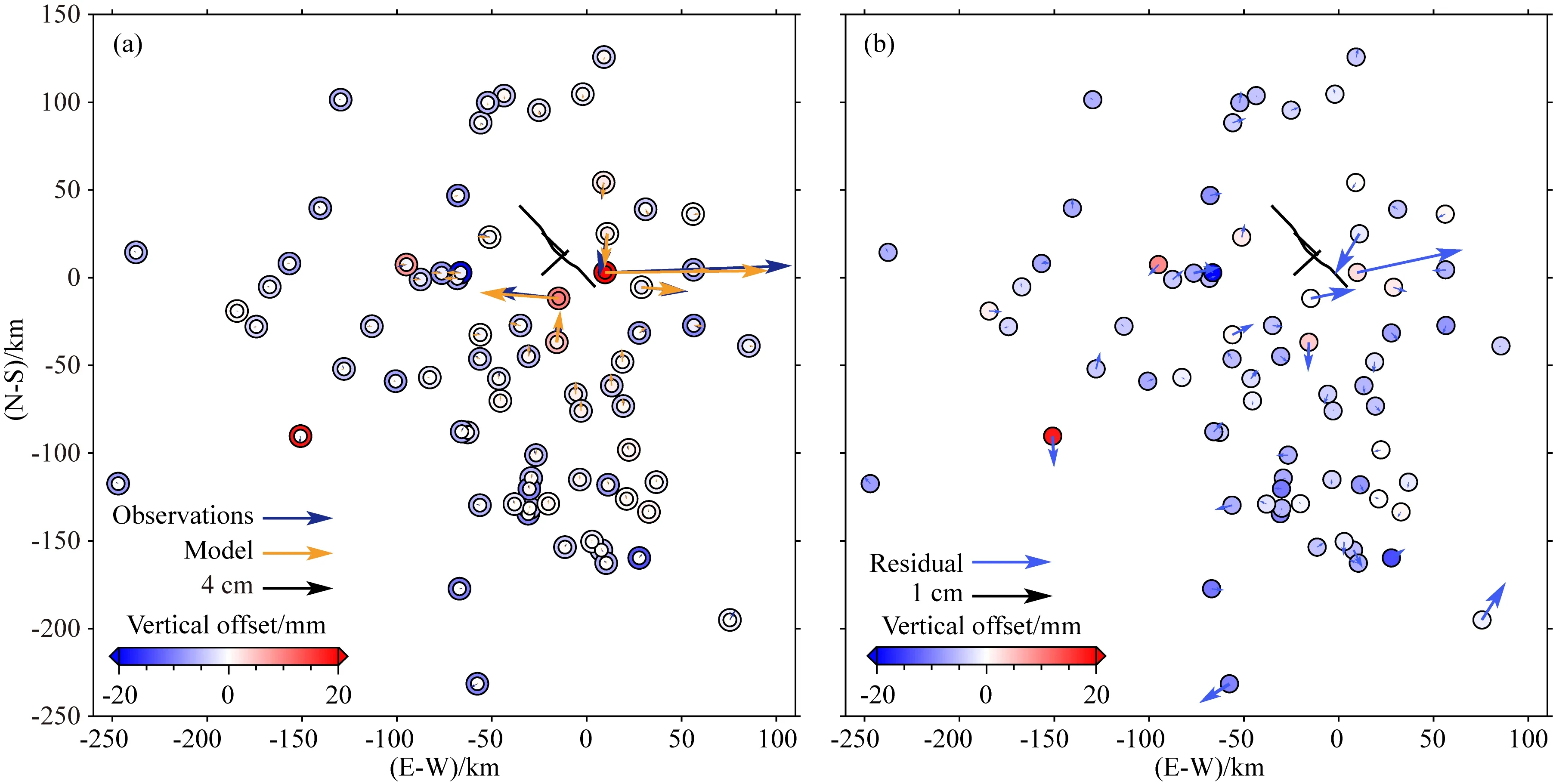
图8 MW6.4前震GPS形变场及其残差(a) 中蓝色和黄色箭头分别表示GPS水平方向观测值和模拟值，每个测站的彩色圆圈表示垂直方向观测值(外圈)和模拟值(内圈)； (b) 中蓝色箭头表示水平方向残差，彩色圆圈表示垂直方向残差.Fig.8 GPS deformation measurements of MW6.4 foreshock and its residuals(a) The results with the blue and yellow arrows represent the observed and simulated GPS horizontal displacements, respectively, and colored circles at each station represent the observed (outer circle) and predicted (inner circle) GPS vertical displacements; The blue arrow in (b) denotes the residual in the horizontal direction, and the colored circle indicates the residuals in the vertical direction. The black line represents the fault traces.

图9 MW7.1主震GPS形变场及其残差(a) 蓝色和青色箭头分别表示不同比例GPS水平方向观测值，黄色和红色箭头分别表示不同比例模拟值，每个测站的彩色圆圈表示垂直方向观测值(外圈)和模拟值(内圈)； (b) 蓝色箭头表示水平方向残差，彩色圆圈表示垂直方向残差.Fig.9 GPS deformation measurements of MW7.1 main shock and its residuals(a) The results with the blue and cyan-blue arrows represent different scales of GPS horizontal displacements, the results with the yellow and red arrows represent different scales of predicted displacements, and the colored circles at each station denote measured (outer circle) and predicted (inner circle) vertical displacements; (b) The results with the blue arrow represent the residuals in the horizontal direction, and the results with the colored circle represent the residuals in the vertical direction. The black line represents the fault traces.

图10 InSAR形变值、模型值以及残差(a)和(d)分别为ALOS-2上升轨道T065和上升轨道T066的LOS形变场； (b)和(e)分别为利用协同反演方法得到的模拟形变场； (c)和(f)分别为对应轨道的残差；黑线表示断层迹线.Fig.10 The observed InSAR displacements, the modeled displacements and their residuals(a) and (d) are the LOS deformation fields of the ALOS-2 ascending track T065 and T066, respectively; (b) and (e) are the predicted displacements obtained by the cooperation inversion method, respectively; (c) and (f) are the residuals of the corresponding tracks, respectively; The black line represents the fault traces.

综上所述，采用协同反演方法可以有效地分离出该地震序列InSAR同震形变，并联合GPS数据反演了该地震序列的滑动分布，与已有研究进行了对比分析，证明了本文方法在同震滑动分布反演中的有效性.

4 结论

本文采用的协同反演方法为反演序列地震滑动分布提供了一种新的思路.本文通过模拟实验，利用联合反演方法和协同反演方法进行序列地震滑动分布反演，验证了本文方法的有效性；此外本文方法无需确定多类数据的相对权比，针对序列地震InSAR数据包含多次地震形变，利用本文方法能够有效地反演出单次地震事件的滑动分布.并将本文方法应用于Ridgecrest地震序列滑动分布反演，结果表明：MW7.1主震滑动主要集中在0～10 km范围，最大滑动量达到4.26 m，位于地表下0～5 km.累积释放地震矩4.49×1019N·m，对应矩震级约为MW7.07.MW6.4前震破裂了一对共轭断层，其滑动主要集中在0～10 km范围，且东北向断层破裂更大，最大滑动量达到1 m，位于地表下2～4 km处.累积释放地震矩5.28×1018N·m，对应矩震级约为MW6.45.反演结果均与USGS公布结果较为一致.根据模拟实验与Ridgecrest地震序列反演结果表明，采用协同反演方法能够针对InSAR无法分离出单次地震同震形变场的情况下，利用GPS数据反演的结果作为先验信息，从而分离出单次地震的InSAR形变数据，使InSAR数据能够有效用于单次地震的滑动分布反演中，一定程度上突破了InSAR数据在时间上的局限性.

致谢感谢审稿专家对本文提出的宝贵意见.文中部分图件是采用开源软件GMT(Generic Mapping Tools)绘制，在此表示感谢.感谢许光煜博士提出的宝贵建议和帮助.