超声纵波换能器用于平测时的测距修正方法研究

杨 予，包 挺，王 毅，徐 浩

(浙江理工大学 建筑工程学院，浙江 杭州 310018)

1 引 言

超声平测法是指将纵波发射和接收换能器置于构件同一侧表面上测量波速的方法[1,2]。该方法具有测点布置方便灵活的特点，在工程中得到了广泛应用，尤其常见于利用超声脉冲波速法(ultrasonic pulse velocity)来诊断建筑材料的特性。例如:Mesquita E等[3,4]采用换能器平测(indirect transmission)布置方式对古代教堂的粘土砖的均匀性进行了研究；Gehlot T等[5]中采用平测、角测(semi-direct transmission)和对测(direct transmission)方式对新建办公建筑的梁柱构件进行了UPV波速与混凝土抗压强度关联性的研究；Lee C H等[6]利用特制换能器研究了岩石试样的对测与平测波速的相关性和修正系数。

采用平测布置方式测量波速时的一个难题是如何确定换能器之间的真实传播距离。例如:Benaicha等[7]采用换能器边缘至边缘的距离计算纵波波速，结果得到高性能纤维混凝土(high performance fiber-reinforced concrete)平测波速明显大于对测波速的结论，实验中换能器固定方式为在混凝土试件上表面自然放置；Adamatti D S[8]利用平测方式对钢筋混凝土结构进行了评价，实验中波速计算距离取换能器中心距，耦合剂采用凝胶，换能器固定方式不详；徐存东[9]取换能器内边距进行波速计算来判断混凝土冻伤层厚度，实验中的换能器固定方式不详；Yaman I O等[10]认为真实传播距离可能在换能器内边距和外边距之间变化，由于没有合适的方法确定真实传播距离，文中同时采用换能器内边距、中心距和外边距3种方式来分析波速，实验中采用的换能器固定方式为在试件上表面自然放置。

由上述文献可见，现有研究中关于超声波平测法的应用尚有如下两点不足:(1)换能器之间真实传播距离的取值不明确；(2)波速测量时换能器的放置或固定方式不一致。

本文研究目的在于给出超声纵波换能器用于平测时的传播距离修正方法，以使其在工程中得到更为合理和准确的应用。具体工作有:(1)根据弹性波理论分析采用换能器平测布置代替对测布置测量波速时的实际物理意义；(2)根据常见纵波换能器构造对超声波真实传播距离进行分析；(3)通过长条形混凝土试件的切割—声时测量实验对平测和对测的真实传播距离关系进行验证。

2 实际物理意义分析

采用超声脉冲方法和纵波换能器进行测量时，垂直于测试面输入的声压将在弹性体中产生沿该方向传播的P(纵)波，而由于泊松比的关系，平行测试表面的边缘层也会对应产生P(纵)波，此外，按弹性波理论还有沿表面传播的R(表面)波，如图1所示。

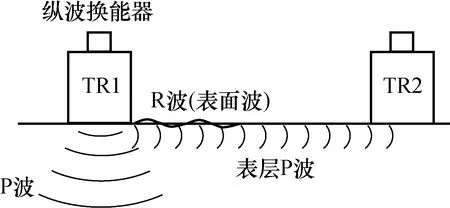
图1 纵波换能器用于平测波传播示意图Fig.1 Schematic diagram of P-wave transducer used for indirect transmission

根据弹性波理论，P、R波波速之间有比例关系[11]:

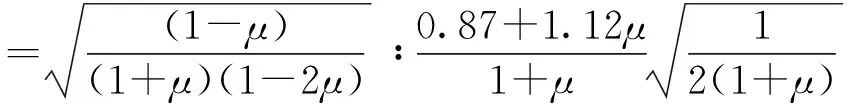
(1)

式中：cl为P波波速，cr为R波波速；μ为材料泊松比，对于普通混凝土和砂浆等建材可取0.18～0.28[12,13]，代入式(1)可知，当采用平测布置进行波速测量时，测得的首波到达时间应为沿表层传播的纵波的到达时间。

由于换能器采用平测和对测布置的传播路径不同，采用前者代替后者的实际意义是:利用材料表层某一路径上的物理特性来近似其内部某一路径上的物理特性。对于被测材料来说，如能保证其均匀各向同性，则这种代替具有合理性。

3 真实传播距离分析

纵波换能器的常见结构如图2所示，其一般原理是利用压电晶片的厚度振动模式激发纵波。在激发或接收纵波时，由于压电晶片与保护膜、换能器外壳和耦合剂、测试面之间复杂的材料边界接触耦合效应，以及换能器制造加工中的随机误差，其底面声源中心点O′的位置一般与底面几何中心点O存在一定偏差。为便于推导，设其径向距离偏差为δ，并假定该δ仅与换能器的构造、信噪比、边界接触耦合效应有关，而与被测材料的具体性质无关。

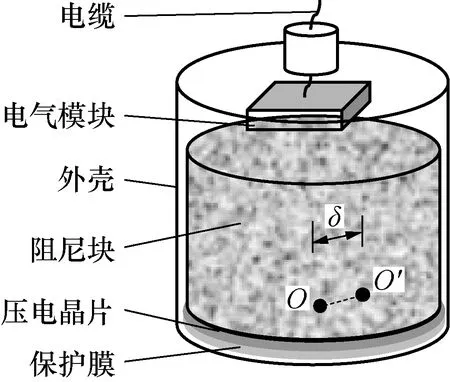
图2 常见纵波换能器结构示意图Fig.2 Structure diagram of common longitudinal wave transducer

当换能器采用对测布置时，如图3所示。O为底面几何中心点；O′为发射换能器声源中心点；O″为接收换能器声源中心点。真实传播距离为换能器底面声束入射点和接收点之间的距离O′O″，可以推出，O′O″与换能器底面几何中心点之间的距离OO=L1有最大值为γ=(1-cosα)=2sin2[(δ1+δ2)/(2L1)]的偏差，如果名义测距L1≫δ1+δ2，还可认为该偏差最大值为2[(δ1+δ2)/(2L1)]2。可以看出，该理论偏差为δ/L的平方项，对声时测量结果造成的影响一般情况下可忽略。

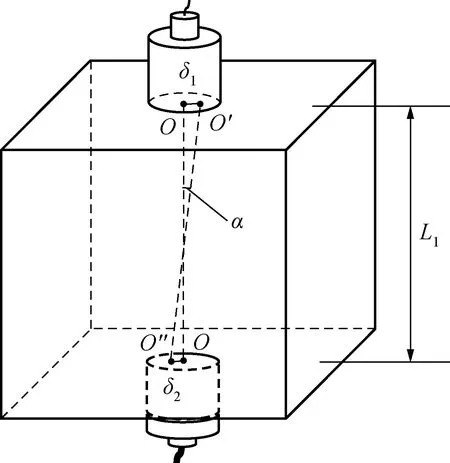
图3 对测布置真实传播距离示意图Fig.3 Schematic diagram of actual propagation distance of direct transmission

当换能器采用平测布置时，如图4所示，可以推出，超声波真实传播距离为换能器声源中心点之间的距离O′O″与换能器底面几何中心点之间的距离OO有最大值为γ=[(δ1+δ2)/L1]的偏差。可以看出，该理论偏差为δ/L的一次项，对声时测量结果造成的影响相对较大。

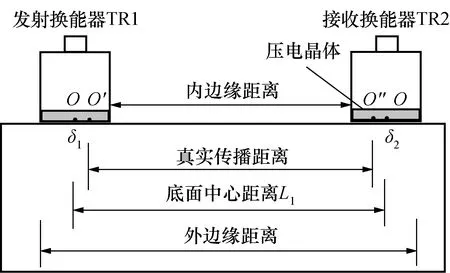
图4 平测布置真实传播距离示意图Fig.4 Schematic diagram of actual propagation distance of indirect transmission

根据前面对δ的分析可知，一般情况下真实传播距离与换能器内边缘、外边缘或中心距都不相等。而且，如果未采取措施来保证两个换能器每次测量时在测试面上所处的相对位置和与接触面耦合情况的一致性，该传播距离将在每次重新放置换能器时发生随机变化，如图5所示。

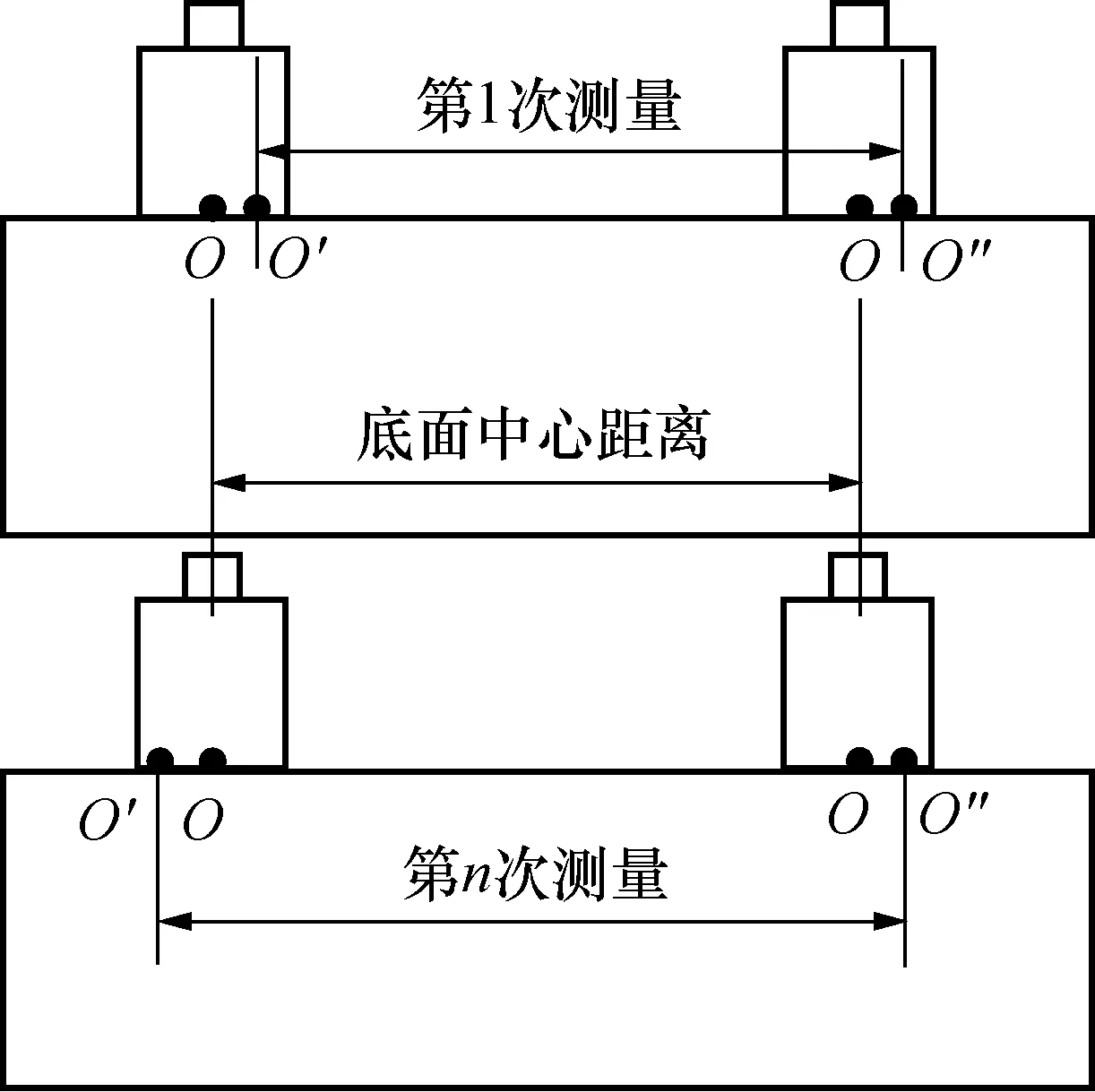
图5 真实传播距离随机变化示意图Fig.5 Schematic diagram random variation of actual propagation distance

在文献[7,10]中所采用的测量多个距离声时和作时-距图的方法，实质上可视为通过对多个测距偏差取平均，来消除δ的随机性对声时测量结果的影响，但该方法仍不能考虑真实传播距离与名义测距(工程中常采用换能器内边缘、外边缘或中心距)的不同带来的影响。

根据前面的论述，可考虑将对测和平测布置方式测得的声时做对比，来推算平测布置时换能器之间的真实传播距离。具体思路是:首先，采取措施保证测量时换能器相对位置和接触面耦合情况的一致性；然后，在各向同性材料试件上进行切割和测量实验得到相同名义测距上的声时，见图6，利用时-距图和最小二乘法得出真实波速；最后，利用平测和对测的声时差推算出平测布置的真实传播距离。

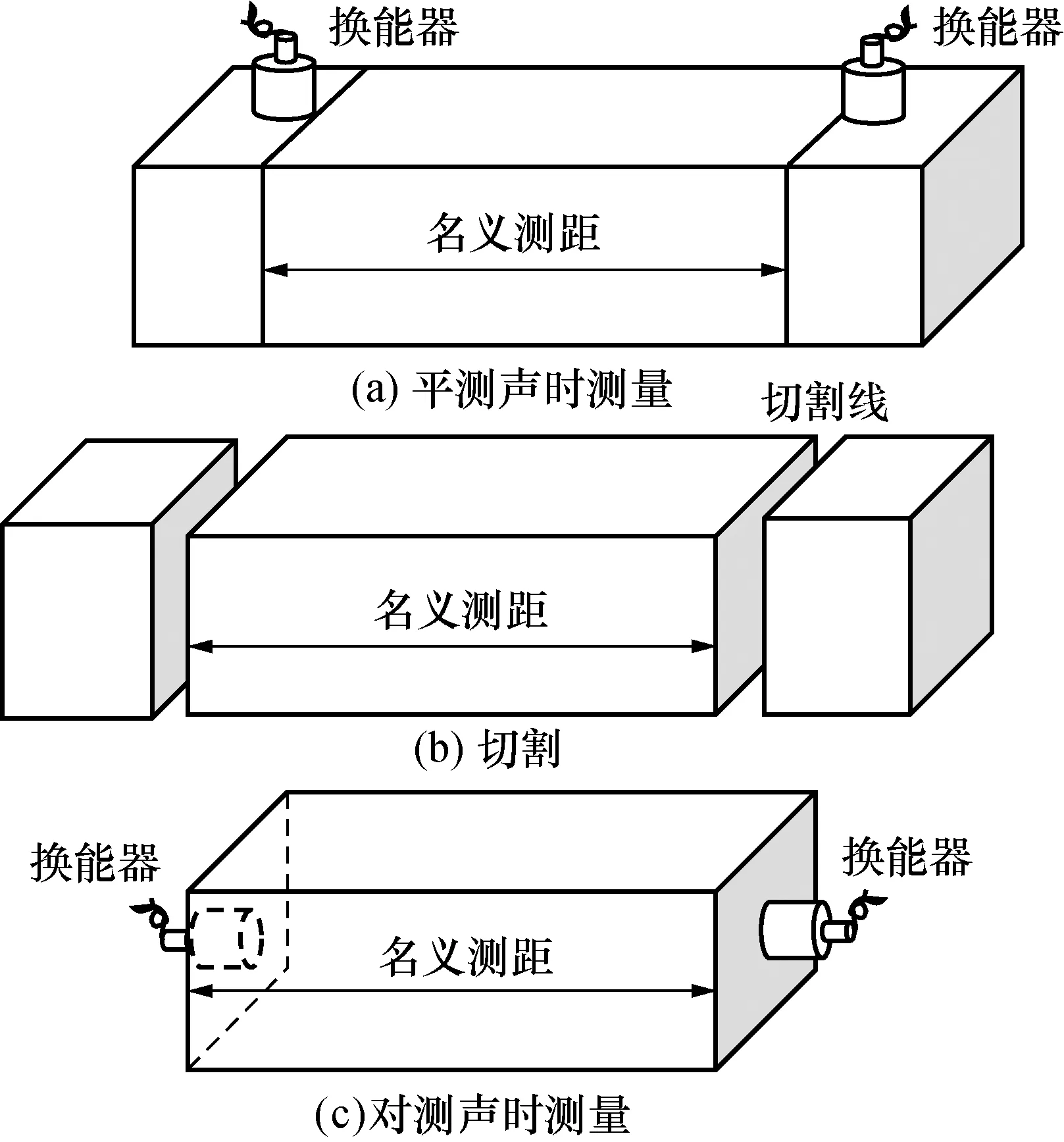
图6 切割-测量实验示意图Fig.6 Schematic diagram of cutting-measurement experiment

4 真实传播距离测定实验

4.1 实验材料

本节利用试件的切割-波速测量实验来研究对测-平测测距修正方法。为能进行多个测距的对比，选取尺寸为120 mm×120 mm×1 200 mm的长条形试件。另一方面，为保证均匀各向同性和避免粗骨料分布不均以及减少切割时的振动冲击对波速测量结果所产生的影响，采用泡沫混凝土制作试件。制作时采用的材料为PO32.5普通硅酸盐水泥、河砂、自来水和QW-100发泡剂，配合比为水:水泥:砂=0.33:1:0.11，发泡剂掺量按发泡体积 0.033 4 m3每立方米计算；采用机械搅拌使泡沫均匀分布，浇入模具，拆模养护28 d之后进行实验。

4.2 实验装置与换能器固定方法

波速测量采用带示波器的NM4B型脉冲混凝土超声仪，选用底面直径为40 mm，中央工作频率为 40 kHz 的纵波换能器，换能器与测试面之间的耦合剂选用凡士林。

由文献[14]中的研究可知，超声波纵波在固体中传播速度受接触压力的影响。为消除换能器朝向和接触压力的随机性对声时测量结果的影响，本文设计制作了专用夹具对换能器进行固定，其原理为在换能器外表面作出用于空间对位的标志线，并在夹具卡座上作出刻度线，固定时通过对齐标志线和刻度线来保证两个换能器的空间对位关系在每次测量时都一致，如图7所示。

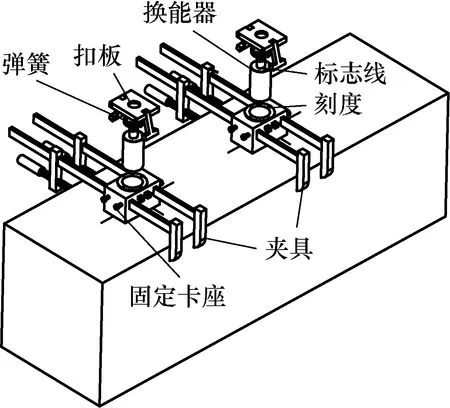
图7 用于固定换能器的专用夹具示意图Fig.7 Schematic diagram of special clamp for fixing transducer

此外，通过调整该夹具的弹簧和扣具长度还可保持每次测量时的压力为固定值，参考文献[15]中的换能器固定压力与波速测量值关系，实验中取压力值为50 kPa。

4.3 实验过程

4.3.1 平测测量

平面测量示意图如图8所示。选择试件的光滑面，在上面依次标记出0 mm,100 mm，200 mm,…,1 000 mm 的测距线，取名义测距L1为换能器内边缘距，并按图8(a)利用上述夹具进行空间对位固定，然后按测距从小到大进行声时测量，实测照片见图8(b)所示。

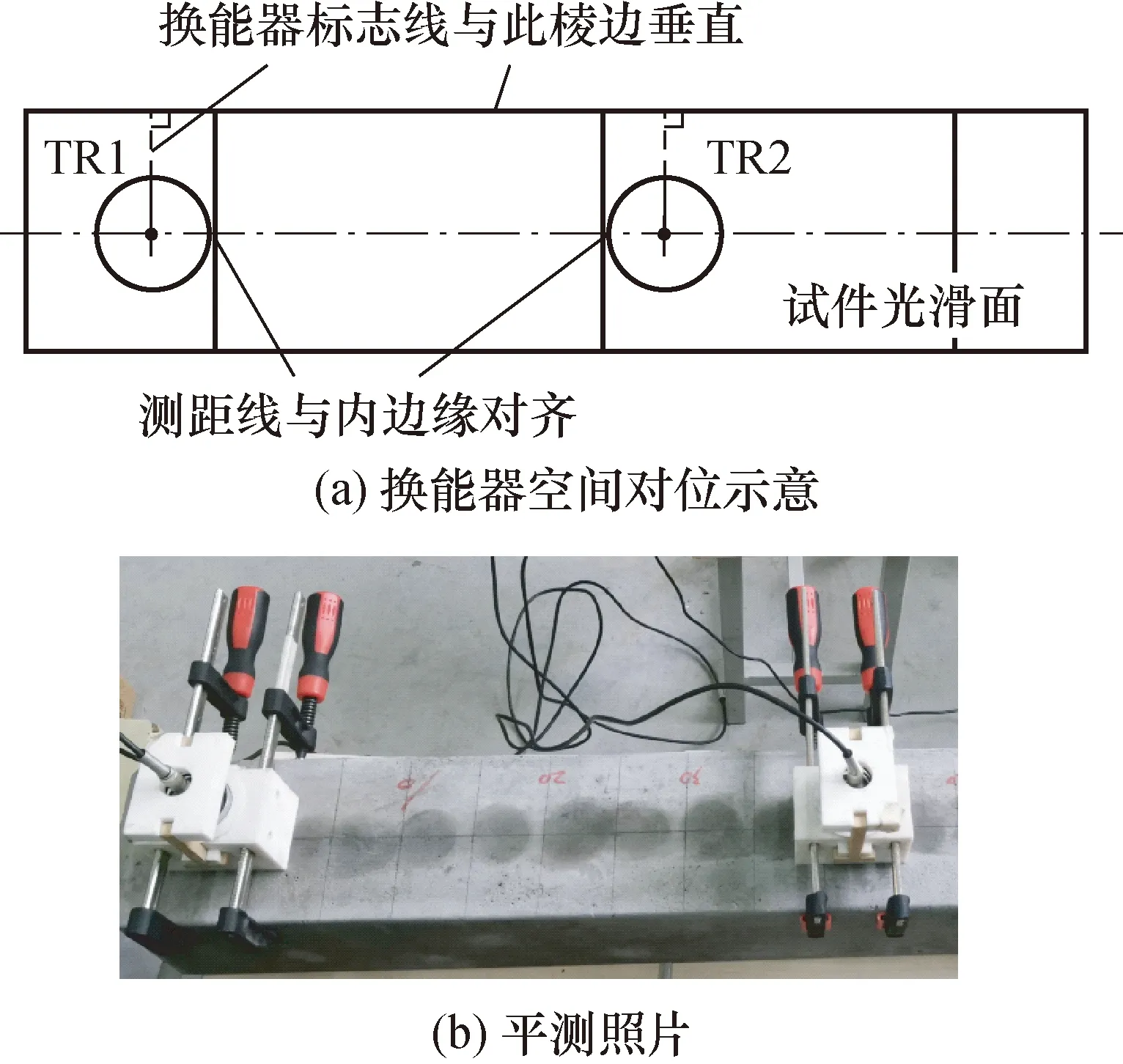
图8 平测测量示意图Fig.8 Schematic diagram of indirect transmission measurement

4.3.2 对测测量

图9为对测测量示意图。

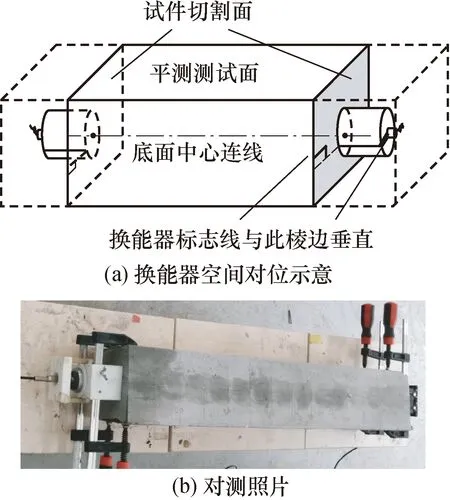
图9 对测测量示意图Fig.9 Schematic diagram of direct transmission measurement

在完成平测测量后，从试件一端到另一端按前述测距线依次进行切割和对测，切割时采用金刚石锯片，并利用机械夹具固定和对齐以保证试件上的切割面平行；切割完成后，将换能器用专用夹具按形心对形心的方式固定于切割面上，并按图9(a)的方式进行空间对位，然后进行声时测量，实测照片见图9(b)所示。

4.3.3 声时判读与处理

为保持判读方式的一致性和减少读数误差，采用文献[16]中给出的固定幅值读数法，对每个测距判读记录16次，并在去除其中最大和最小的3个值后，将余下的10个值求平均值作为该测距的声时。

5 结果与讨论

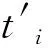
表1 平测与对测平均声时测量结果Tab.1 Measurement results of direct and indirect transmission

考察在每一个测距增量上的声时增量，可得图10所示的直方图。

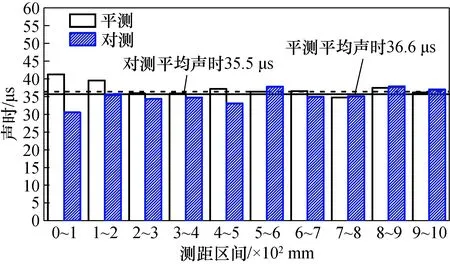
图10 两种布置方式的声时增量直方图Fig.10 The incremental histogram of the two methods

由图10可见，除受径向距离偏差δ1和δ2影响较大的0～100 mm测距增量外，其它测距增量上的平测和对测声时增量均较为接近，在不计入第一个测距的条件下，平测声时增量平均值为36.6 μs，对测声时增量平均值为35.5 μs；此外还可以观察到，在相同的测距增量上，对测声时增量与平测声时增量的比值在1上下波动。

由此可知，在取相同测距增量时，试件表层和内部测量路径上的纵波传播速度非常接近，而导致测量结果差异的原因有两个:1)在制作过程中，试件的表层与内部物理特性不可避免地存在一定随机性和变异性；2)进行声时判读时存在随机读数误差，判读结果在一定范围内波动。因此可以得出:利用试件表层测量路径上的物理特性来近似替代其内部测量路径上的物理特性在一定条件下是可行的。

时-距线性回归与修正测距的计算的数据分布图如图11所示。

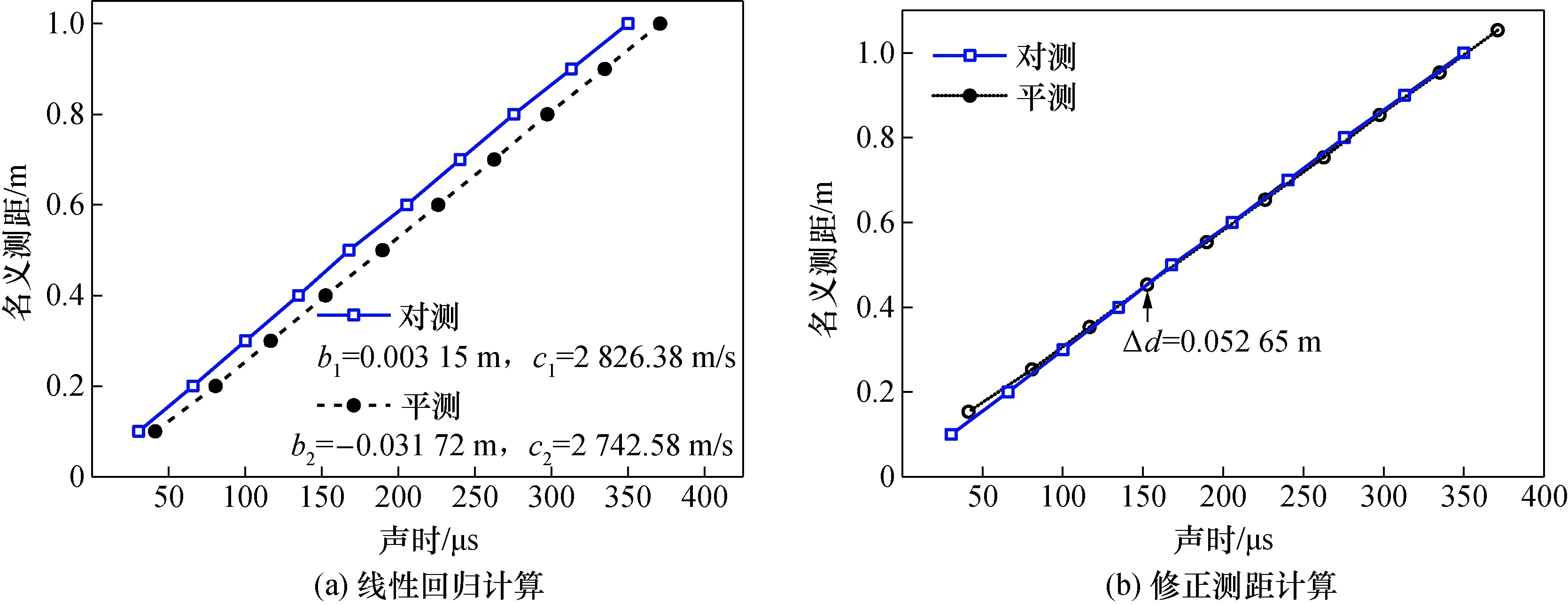
图11 时-距线性回归与修正测距的计算Fig.11 Time-distance linear regression and calculation of correction distance

根据表1中的测量结果可绘制声时-测距图，见图11(a)。将对测和平测数据作最小二乘法线性回归得到y=b+cx形式的直线方程(斜率c为波速),其中对测法对应的波速值c1=2 826.38 m/s，b1=0.003 15 m，平测法对应的波速值c2=2 742.58 m/s，b2=-0.031 72 m。两种测量方式求得回归波速的相对误差为3.0%，说明试件所采用的材料基本符合均匀各向同性假定。

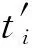
(2)

取最小值。

对式(2)中的Δd求导，并令其为0，得到：

(3)

式中：n为实验总测距数(建议取5～10个)。该公式即为求修正测距的计算公式。

对均匀各向同性材料，在实际测量中可采用平测布置测出声时，然后按公式(4)求得当量对测波速c1，

(4)

式中：LN为换能器名义测距；t′为平测声时。

表2中列出了以对测布置方式测得各个测距上的波速作为基准时，平测布置方式分别取换能器内边距、中心距、外边距作为计算测距求得的波速以及按公式(4)求出的波速误差情况，表中di取换能器内边距。由计算结果可见当di≤200 mm时采用中心距计算波速误差最小，也可在公式(4)中取Δd=0，在di≥300 mm时采用公式(4)计算波速误差最小(<2%)。

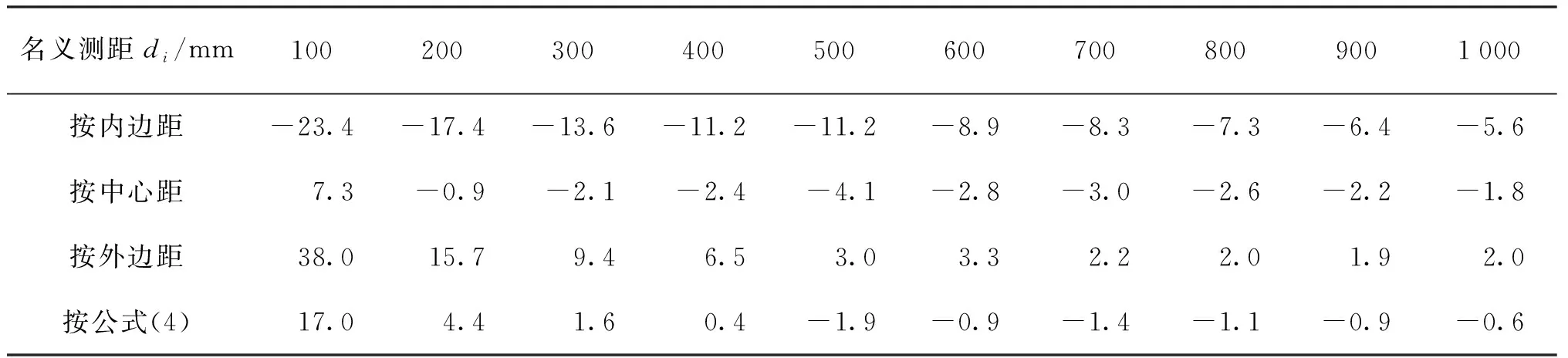
表2 平测取不同计算测距求得波速与对测误差

需要注意的是，公式(3)和(4)中的修正测距对应的是在本文实验中所采用的换能器、固定压力和平测与对测布置的空间对位固定方式，在实际应用中须保持换能器、固定压力、空间对位方式不变，否则应重新测定Δd。

6 结 论

为得出平测布置时的真实传播距离，本文给出了一种求平测-对测波速换算修正测距的方法:

(1) 采用各向同性材料制作条形试件，选取换能器按一定的空间对位方式和固定压力进行多个测距的平测和切割-对测实验以获得声时-测距数据；

(2) 在对测实验获得的声时-测距数据的基础上做最小二乘法回归分析得到直线方程，并在该方程的基础上，再次利用最小二乘法将平测实验的声时-测距数据代入公式(3)获得平测修正测距Δd；

(3) 在平测法的名义测距上叠加该修正测距，即可按公式(4)求出对测当量波速；

(4) 该修正测距对应的是在测定实验中所采用的换能器、空间对位固定方式和固定压力，使用时须保持这些参数的一致性。

理论和实验研究结果表明：对于本文中的换能器，在名义测距di≤200 mm时可采用中心距计算波速，而di≥300 mm时按平测声时和修正测距求出的波速与对测波速误差小于2%。由此可得以下两点结论:

(1) 超声纵波换能器的平测布置方式可在一定条件下代替对测布置方式进行波速测量，其物理意义为利用材料沿表层测量路径上的特性来近似沿内部测量路径上的特性；

(2) 本文给出的方法可求出平测布置换能器之间的真实传播距离，进而方便地将平测波速转换为对测当量波速。