基于结构保持因子的显微图像滤波质量客观评价指标

崔秋硕，邓可欣，黄晓铧，齐现英，韩丰谈

山东第一医科大学（山东省医学科学院）放射学院，山东泰安271016

前言

随着图像处理技术的发展，显微细胞图像研究成为医学图像处理的一个重要领域［1］。近年来我国不孕不育发病率不断增高［2‐4］，且男性不育比例呈上升趋势，计算机辅助精子质量分析系统因其客观性和准确性已被广泛应用于临床［5‐9］。其中，精子活性等指标主要通过对显微视频中动态精子的提取和跟踪等过程的统计学分析获得。由于精子显微图像具有兴趣目标小、对比度低、前景与背景比例悬殊等特点，图像采集过程中的各种干扰噪声不可避免地会对精子提取准确性及跟踪轨迹的连续性造成一定影响。因此，滤波成为显微图像预处理关键环节之一。现有滤波算法众多，如中值滤波（Median Filtering,MF）［10］、自适应MF［11］、均值滤波［12］、非局部均值滤波［13］、双边滤波［14］等都曾被应用于显微图像滤波领域。但算法对显微图像的滤波效果，大多数文献仅通过主观评价进行衡量。其根本原因是显微图像无法获取不含噪声的标准图像，不能使用峰值信噪比及结构相似指数［13］等宏观图像滤波的质量评价指标。对显微图像滤波来说，目前尚缺乏一种有效的滤波质量客观评价方法，研究一个可以脱离标准图像的显微图像滤波质量客观评价指标已成为一个亟待解决的问题。

本研究从精子跟踪轨迹连续性与滤波图像结构变化之间的相关性角度展开研究，提出一种基于结构保持因子的显微图像滤波质量客观评价指标，该指标可对计算机辅助精子质量分析系统显微图像滤波算法的选取提供量化指导，在图像预处理阶段为计算机辅助精子质量分析系统提供质控方案［15‐17］。

1 不同噪声密度下精子跟踪轨迹的连续性

1.1 精子跟踪轨迹连续性等级

精子视频中既包含静态精子又包含动态精子，将视频序列每帧图像的动态精子提取后，通过目标跟踪算法，可对精子在每帧图像中的位置进行定位。找出每个精子在序列图像中位置即可描绘精子运动轨迹。某精子视频序列部分动态精子的跟踪轨迹如图1所示，其中曲线代表精子轨迹，与曲线相连的黑点代表动态精子。

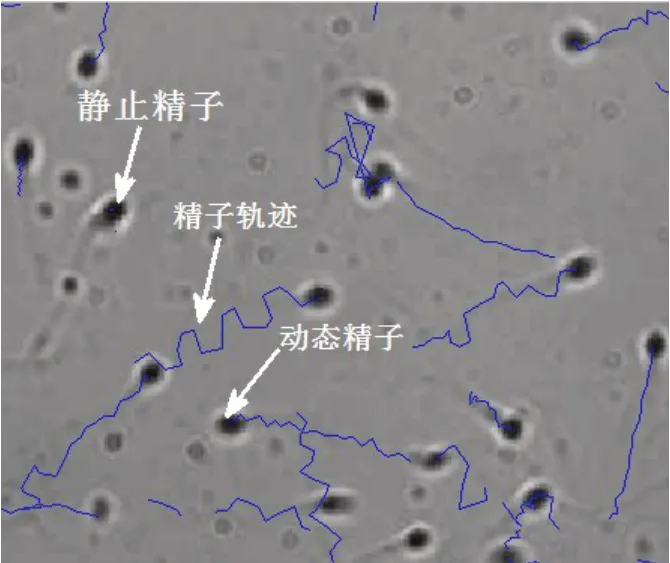
图1 动态精子跟踪轨迹示意图Fig.1 Schematic diagram of dynamic sperm tracking trajectory

图像滤波是精子提取和目标跟踪的关键环节，如果所选滤波算法的性能优良，细节保持能力强，则显微图像滤波后动态精子被成功提取的可能性增大，其运动轨迹的连续性好；反之，如果滤波算法对图像细节破坏严重，或残留噪声较多，则容易出现精子提取失败、跟踪轨迹连续性降低等现象。因此，在选定精子提取和目标跟踪算法后，精子运动轨迹连续性与滤波图像结构保真度有关，在一定程度上可反映滤波算法的去噪性能。本研究以视频序列中加入随机脉冲噪声为例，分析算法滤波性能、滤波图像直方图、跟踪轨迹连续性三者之间的内在联系。

精子显微图像采集速率一般设为25 帧/s，选前20 帧进行精子跟踪足以反映其轨迹连续情况。为方便对轨迹连续程度进行评价，将其分为4个等级。（1）I级：连续等级，20 幅图像中精子未出现丢失现象，轨迹不存在断点；（2）Ⅱ级：轻微断点，20 幅图像中精子在少于4 幅图像中出现分割失败和跟踪丢失；（3）Ⅲ级：严重断点，20 幅图像中精子在超过5 幅图像中出现分割失败和跟踪丢失；（4）Ⅳ级：无轨迹，动态精子在20幅图像中均无法成功分割，无法进行跟踪。

1.2 算法滤波性能与跟踪轨迹连续性的相关性

实验室与合作医院收集了相关精子视频，将编号为1和2的两个精子视频分别加入密度Q为20%～60%的随机脉冲噪声，选择滤波性能较好的基于同源像素（Homogeneous Amount Based, HAB）滤波算法［18］、方向加权中值（Directional Weighted Median，DWM）算法［19］、基于方向信息与中智不确定性融合的滤波算 法（Filter based on Direction Information and Neutrosophic Indeterminacy, FDINI）［20］对图像进行滤波，然后采用最大类间差法对滤波视频进行精子提取与跟踪。

以1 号视频为例，分析同一噪声密度下对应3 种算法滤波图像的精子轨迹变化规律。实验发现，当噪声密度Q低于20%，3 种算法的跟踪轨迹无明显区别，跟踪级别属于连续等级。在30%～60%噪声密度下，3 种滤波算法对1 号视频滤波后的精子跟踪轨迹如图2～图5所示。由图可见，噪声密度为30%时，FDINI 算法的跟踪轨迹保持连续，HAB 算法的轨迹出现轻微断点，DWM 算法的轨迹保持连续；噪声增加到40%时，FDINI 算法的跟踪轨迹保持连续，HAB算法的轨迹出现严重断点，DWM 算法的轨迹开始出现轻微断点；噪声密度增加到50%时，FDINI 算法继续保持运动轨迹连续，而HAB 精子跟踪失败的情况更加严重，DWM 算法已无法正确提取精子，跟踪情况降低到无轨迹级别；噪声继续增加到60%时，HAB和DWM 算法的轨迹连续性下降至无轨迹级别，FDINI算法也降至严重断点级别。

相似地，在20%～60%噪声密度下，分别利用3 种算法对2 号视频进行滤波处理。1 号视频和2 号视频用3 种算法滤波后，其对应的精子轨迹连续性如表1所示。

综合分析图2～图5和表1，可以得出如下结论：噪声较低时，3 种滤波算法对精子跟踪影响较小，其轨迹连续性较高；但随噪声密度增加，精子跟踪轨迹连续性开始出现较大差别，这不但说明同一种滤波算法的去噪性能随噪声密度增加而下降，而且说明不同算法在同一噪声密度下的滤波性能存在较大差异，即它们对图像细节保持能力是不同的。算法滤波性能下降到一定程度，图像细节受损严重时可能出现精子提取和跟踪失败，运动轨迹出现断续情况，甚至达到无轨迹级别。

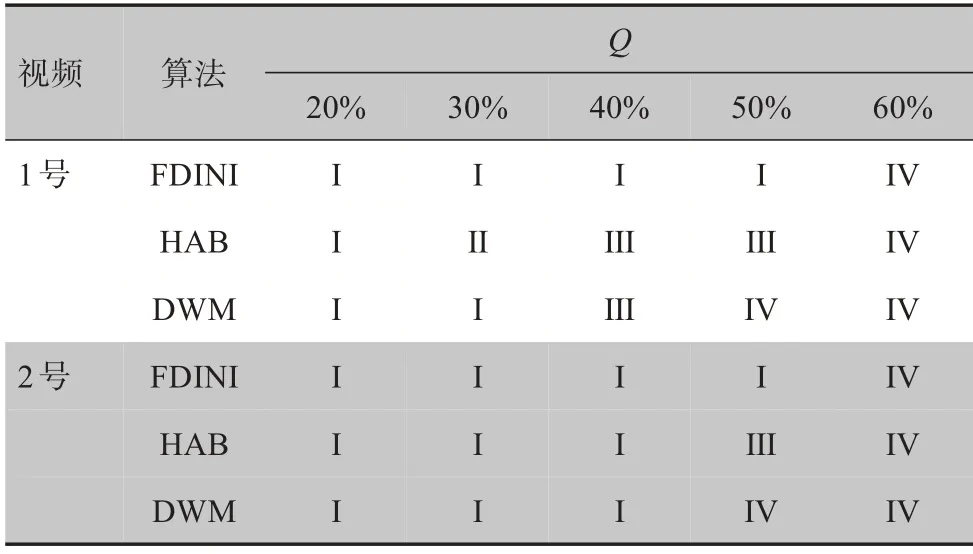
表1 不同噪声密度下3种滤波算法的精子轨迹连续性等级Tab.1 Continuity levels of sperm tracking trajectory obtained by 3 different filtering algorithms under different noise densities

图2 3种算法降噪对应的精子跟踪轨迹（Q=30%）Fig.2 Sperm tracking trajectories obtained by 3 different filtering algorithms(Q=30%)

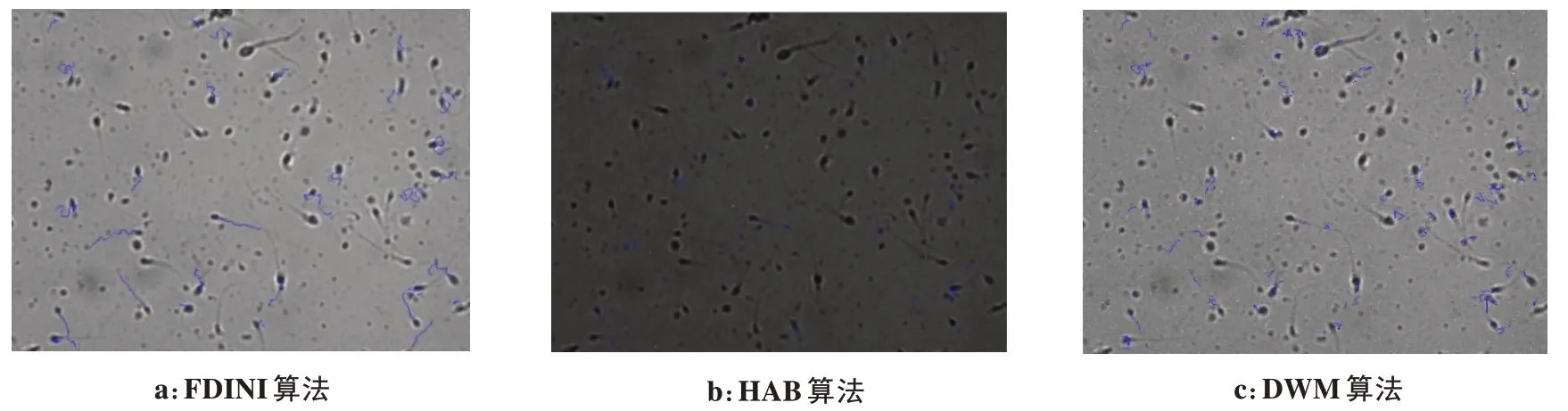
图3 3种算法降噪对应的精子跟踪轨迹（Q=40%）Fig.3 Sperm tracking trajectories obtained by 3 different filtering algorithms(Q=40%)

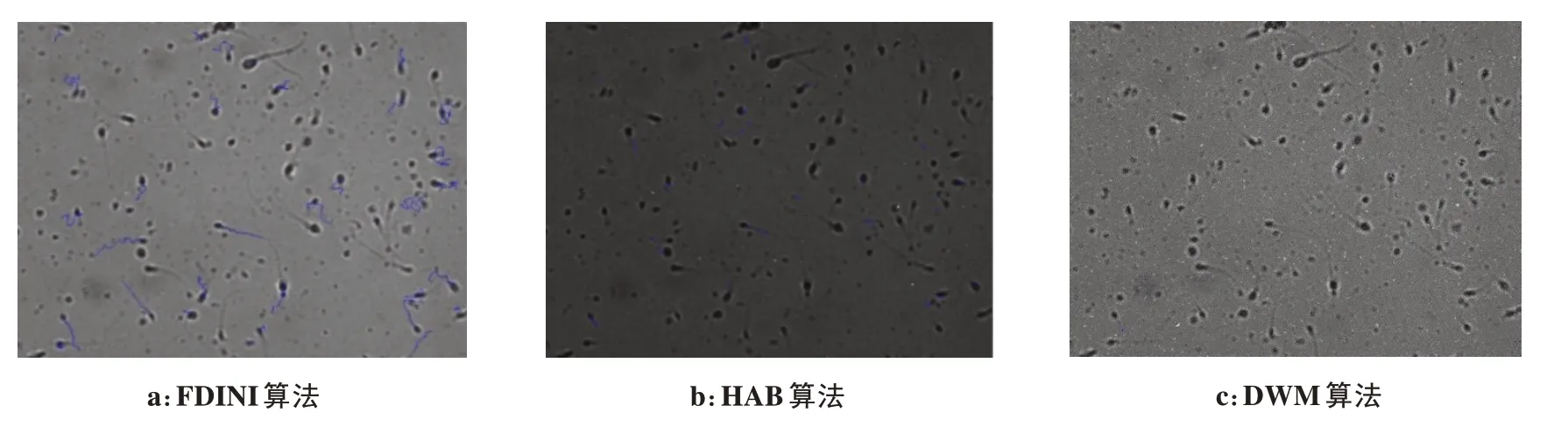
图4 3种算法降噪对应的精子跟踪轨迹（Q=50%）Fig.4 Sperm tracking trajectories obtained by 3 different filtering algorithms(Q=50%)

图5 3种算法降噪对应的精子跟踪轨迹（Q=60%）Fig.5 Sperm tracking trajectories obtained by 3 different filtering algorithms(Q=60%)

2 跟踪轨迹连续性与滤波图像直方图相关性

直方图可反映图像像素灰度分布情况，因此不同噪声密度下滤波图像直方图可反映滤波算法对图像细节的改变情况。本研究首先观察同一滤波算法在低噪声密度和高噪声密度下滤波图像直方图变化情况。MF属于基本滤波方法，相对改进的HAB、DWM、FDINI这3种滤波算法来说，其滤波效果属于最差。为了突出不同滤波算法对图像结构的影响，在此给出4种算法对同一帧图像滤波后的灰度直方图。以2号视频在20%和60%两种噪声密度滤波图像为例，4种算法对应的灰度直方图如图6～图7所示。

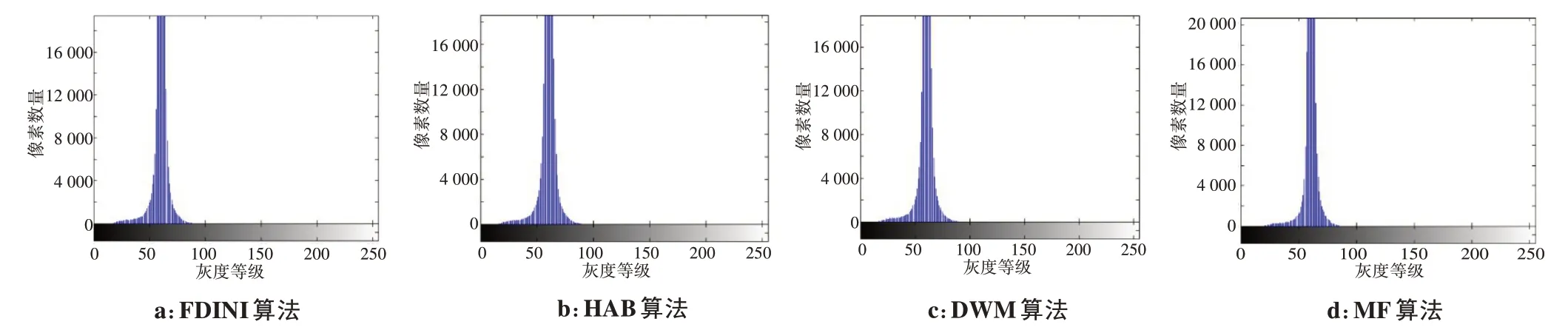
图6 4种算法降噪的灰度直方图（Q=20%）Fig.6 Gray-level histograms of denoised images using 4 different filtering algorithms(Q=20%)

噪声为20%时，4 种算法滤波图像的像素灰度主要集中在50～80 左右，直方图形状窄而高；噪声为60%时，像素灰度分布变得分散，直方图形状变得宽而低，这种趋势在图7c、d 中更明显。这说明不同噪声下，滤波图像的灰度分布发生了较大变化。由表1已知，噪声为20%时4种算法的跟踪轨迹都属于连续级别，噪声为60%时均下降为无轨迹级。由此可得到以下结论：随噪声增加，算法降噪性能下降→滤波图像直方图结构发生改变→图像结构受损严重→轨迹连续性恶化。因此，同一噪声密度下如果降噪图像对应轨迹连续性差，则说明图像结构受损严重，对应算法的滤波性能低。反之，则说明算法的滤波性能高。因此，可从滤波图像的结构保持程度对算法滤波性能进行衡量。

图7 4种算法降噪后的灰度直方图（Q=60%）Fig.7 Gray-level histograms of denoised images using 4 different filtering algorithms(Q=60%)

3 基于直方图统计的结构保持因子

3.1 结构保持因子的推理计算

由上述实验可见，算法去噪性能、灰度直方图变化、精子跟踪轨迹三者之间确实存在一定因果关系。分析图6、7 与表1，可发现：对某一滤波算法而言，如果低噪声和高噪声两种情况下滤波图像直方图形状差别较大，说明算法在高噪声密度时会导致图像像素灰度分布发生较大变化，对图像细节或结构造成较大影响，有可能发生精子提取不准确或精子跟踪失败等问题，该去噪算法不利于当前精子显微图像；反之，如果低噪声密度和高噪声密度下滤波图像灰度分布几乎不变或变化很小，则说明算法去噪性能和结构保持性能良好，有利于当前精子显微图像滤波。据此，本研究提出将结构保持因子作为滤波算法对精子显微视频去噪性能客观评价指标，其具体计算过程如下。

设d={d0,d1,d2,…,dj} 表示噪声密度集合，噪声密度d0下所选精子视频第i帧滤波图像的像素灰度分布可用式（1）表示。

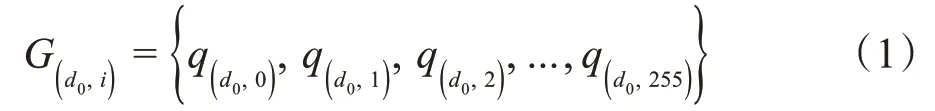
同理，噪声密度为dj时，第i帧滤波图像像素在0～255之间的灰度分布为：

一般地，滤波算法在低噪声情况下的滤波效果优于高噪声，如果在d0和dj两种不同噪声密度下，滤波图像发生灰度变化的像数越少，则说明算法在噪声密度较大时其细节保持能力越强。一帧图像在两种噪声密度下灰度发生变化的像素数量可表示为：

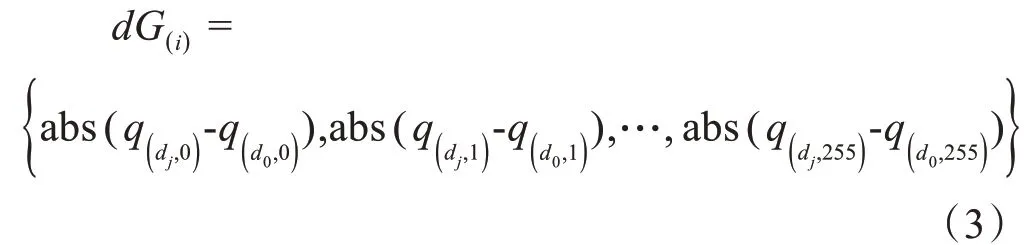
化简式（3）可得：

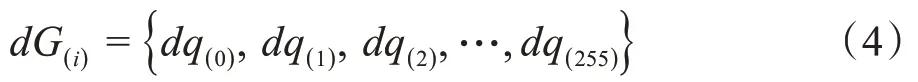
其中，dq(0)表示两种噪声密度下，灰度为0的像素个数变化量，dq(255)表示灰度为255的像素个数变化量。

在式（4）中，如果dG(i)每项的数值较小，说明与较低噪声情况相比，较高噪声密度下滤波图像像素灰度变化量较小，对应滤波算法的细节保护能力强。反之，如果dG(i)集合每项的数值较大，说明与低噪声情况相比，较高噪声密度下滤波图像发生灰度变化的像数较多，图像细节受损严重，则该滤波算法的结构保持能力较差。

设视频序列一帧图像的像数总数为m×n，d0和dj两种噪声密度下第i帧图像发生灰度变化的像数总数用式（5）来计算。

设滤波算法的结构保持因子表示为k，则k可用式（6）来计算。

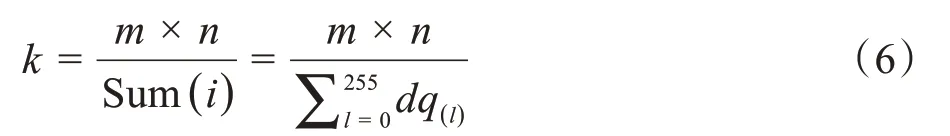
对一幅图像来说，Sum(i)越小，则k越大，说明与低噪声情况相比，该滤波算法在较高噪声情况下，滤波图像灰度发生变化的像数少，即对图像结构保持较好，其滤波性能高；反之，k越小，其滤波性能越差。

3.2 不同滤波算法的结构保持因子

以1 号、2 号视频为例，设d0为20%噪声密度，dj为60%噪声密度，每个视频选前20帧图像进行比较，4种算法对应的结构保持因子k如图8所示。

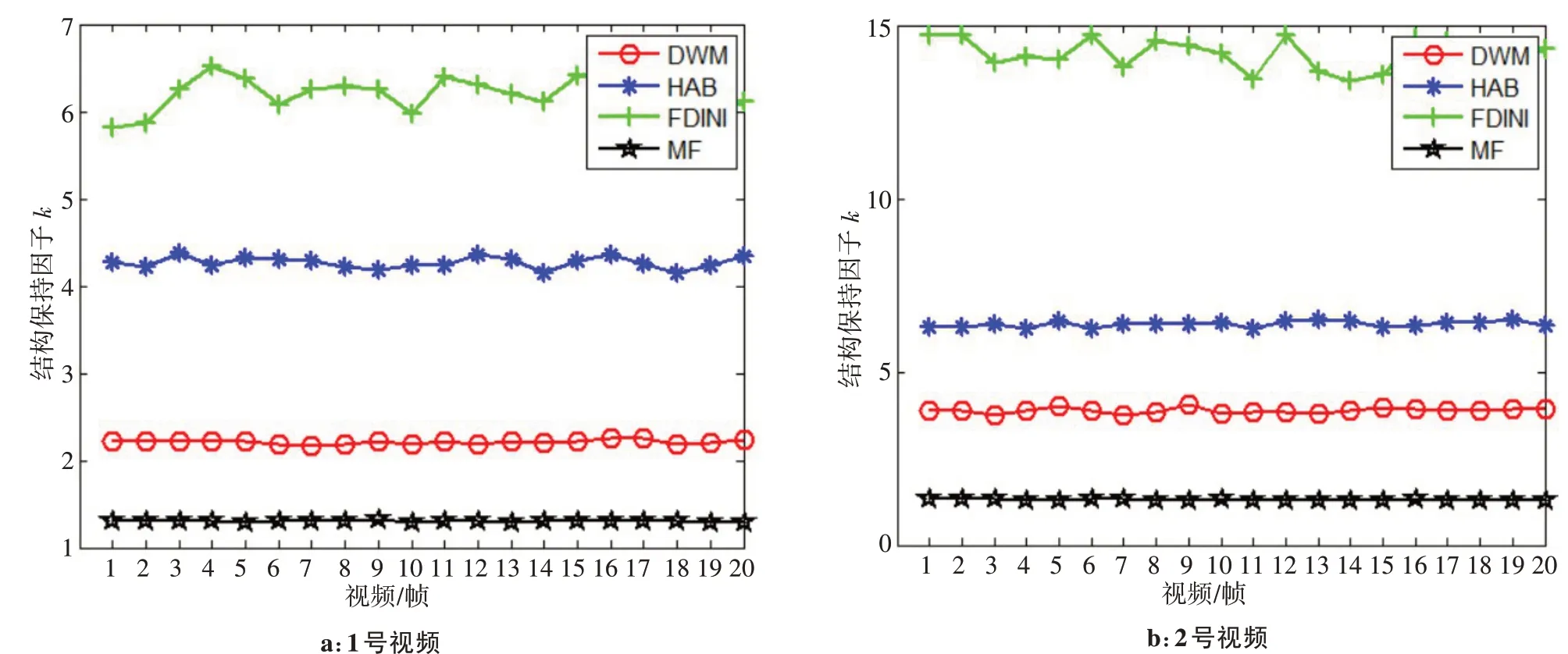
图8 4种滤波算法的结构保持因子Fig.8 Structure preservation factors of 4 kinds of filtering algorithms

对1 号视频来说，FDINI 算法的k值在6～7 左右，HAB算法的k值在4～5左右，DWM 算法的k值在2左右，MF算法的k值在1.5左右；对2号视频来说，FDINI 算法的k值在15 附近波动，HAB 算法的k值在6 左右，DWM 算法的k值在4 左右，MF 算法的k值在1左右。无论是1号视频还是2号视频，4种滤波算法中，FDINI 算法具有较大结构保持因子，对显微图像的去噪性能最好，HAB 算法优于DWM 算法，但低于FDINI算法，而MF算法具有最小的结构保持因子，对显微图像的去噪性能最差。

表1得到的精子跟踪轨迹连续性与算法去噪性能的关系与图8得到的结论相一致，说明k越大，同一视频序列的精子跟踪轨迹连续性等级越高，反之则连续性越低，进一步证明结构保持因子k作为显微视频滤波性能衡量的有效性。

4 结论

针对显微图像不适合用峰值信噪比及结构相似指数对算法滤波性能进行客观评价的现状，通过研究滤波图像直方图与精子跟踪轨迹连续性的相关性，创新性地提出用结构保持因子来衡量滤波算法对显微图像的滤波性能，并验证了将其作为显微视频滤波能力客观评价指标的有效性。该指标可用于显微视频图像预处理阶段滤波算法的选择依据，从图像处理角度为显微图像预处理提供质控标准。