无人机用燃料电池阴极供气系统建模与控制

赵冬冬，赵国胜，夏磊，方淳，马睿，皇甫宜耿

1.西北工业大学 自动化学院，西安 710129 2.航空工业第一飞机设计研究院，西安 710089

燃料电池是一种通过化学反应，将化学能转变为电能的新型发电装置[1-2]，目前研究的燃料电池有固体氧化物燃料电池、熔融碳酸盐燃料电池和质子交换膜燃料电池(PEMFC)等多个类型[3]，其中，PEMFC因其效率高、噪声小、排放无污染等优点，被认为是未来最具有潜力的无人机用动力源，成为当前的研究热点[4-6]。PEMFC系统通常包含空气供应子系统、氢气供应子系统、湿度控制子系统、温度控制子系统和功率调节子系统5部分。其中，阴极空气供应子系统由空压机、驱动电机、供气歧管、返回歧管等多个部分构成[7]，空压机提供的氧气流量及阴极氧气分压是决定PEMFC系统效率和动态性能的关键因素[8]。

无人机飞行过程中，由高度变化引起的气压变化、温度变化、湿度变化和氧含量变化等，会直接影响到空压机的工作特性，进而对燃料电池的工作性能产生影响[9-10]。另一方面，无人机飞行状态的变化会直接导致燃料电池负载的变化，在燃料电池的加载过程中，能否及时根据负载的变化对阴极供给流量以及阴极压力做出调整，将会直接影响到燃料电池的工作性能[4]。因此，要保证燃料电池系统的高效率和可靠性，对变高度下空压机的特性以及阴极供气系统的研究具有重要意义。

空压机模型一般可通过对大量不同工况下的空压机实验数据拟合得到，但由于空压机试验条件的限制，在全运行范围内的实验数据往往非常有限。此外，查找表的插值程序不是连续可微的，尤其在实验数据有限的情况下，外推不可靠，查找表的预测性会大大降低。Deng等[11]基于数据驱动建立了外源输入的非线性自回归移动平均(NARMAX)空压机模型，并采用循环神经网络(RNN)方法估计模型参数。但空压机进口工况存在很强的相关性，入口温度与压力的变化会影响入口气体密度和流量的大小，增加了在全转速、变高度下神经元的训练难度。CFX、Fluent以及Numeca等软件通过计算流体动力学(CFD)的数值模拟方法模拟空压机输出性能，但该方法计算量大，结果可信度和计算精度都有待提高[12]。偏最小二乘法(PLS)回归算法是一种由化学领域发展形成的新型数据统计分析方法，其在预测空压机性能方面具有强鲁棒性，需要的数据量少且具有明显物理意义的优点。Li等[13]在传统PLS模型的基础上，使用幂函数多项式或三角函数多项式作为基函数(PLSN)，预测离心空压机的压比和效率，PLSN在计算时间最短的情况下预测精度最高，模型结构也更加简单。但PLSN方法并不是对所有的多重共线性问题都有效，某些数据处理的结果会对空压机的建模影响较大。Gravdahl[14]和Chu[15]等在地面常温常压条件下，基于热力学第一定律，从能量传递的角度提出了一种能够在虚拟实验台(VTB)计算环境中进行系统仿真的离心式空压机动态模型。本文基于文献[14-15]中的方法预测摩擦损失，同时考虑了不同高度下温度、气压、密度、雷诺数等环境因素变化，建立了适用于不同高度下的空压机模型。

无人机飞行状态的改变会导致燃料电池负载的剧烈变化，当负载突变时，如果不能根据负载电流的变化，及时对进入阴极的空气流量做出调整，则会出现氧饥饿或氧饱和现象。氧饥饿现象的发生会导致燃料电池输出电压及功率的降低，严重时更会影响燃料电池的寿命[16]。氧饱和现象的发生则会导致功率的浪费，进而降低燃料电池系统的效率[17]。为避免氧饥饿和氧饱和现象的发生，一些文章中提出了根据负载变化对PEMFC阴极过氧比(空压机提供的氧气量与燃料电池实际反应所需的氧气量之比)的控制。Zhang[18]和Baroud[19]等给出了PEMFC阴极供气系统的四阶模型，并基于所给模型，针对过氧比的控制提出了不同的模糊PID控制算法。刘秋秀[20]采用半机理半实验建模的方法给出了PEMFC九阶供气系统模型，并提出了基于系统传递函数的一阶最优自抗扰控制(ADRC)控制策略。王帅[21]给出了四阶供气系统模型，并考虑了空压机电压不能无限制增加的因素，提出了具有约束处理能力的模型预测控制(MPC)。李克雷[22]和郭爱[23]等为保持燃料电池系统净输出功率最大，提出了针对过氧比的电堆电流前馈控制和空气流量模糊反馈控制的策略。浙江大学Chen等[3]给出了阴极供气系统的三阶模型，并基于反馈线性化的方法设计了一个非线性控制器来跟踪控制过氧比保持在最优值。Zhang等[24]针对燃料电池供气系统过氧比提出了一种基于2型模糊逻辑系统(T2-FLS)的自适应鲁棒控制器，基于李雅普诺夫理论分析了该控制系统的稳定性，并通过实验验证了该控制器的实用性和可行性。方思雨[25]提出了一种基于状态量估计器的准无限时域模型预测控制(QHMPC)，采用状态量估计器有效解决了QHMPC算法中一些状态量不易观测的问题，并针对节气门控制设计了相应控制器。Gruber等[26]针对过氧比的控制提出了一种线性模型预测控制算法，所提出的线性MPC采用参数自适应的方法来适应电堆电流的变化。综上所述，目前针对PEMFC阴极供气系统的研究主要集中在对过氧比的控制，对阴极压力控制的研究较少。然而在无人机飞行过程中，高度的变化会直接引起阴极气压的波动，进而对燃料电池输出性能及功率产生较大影响。因此，除了对过氧比的控制，阴极压力的控制也是保证无人机用PEMFC系统高效运行的关键因素[27-28]。

本文首先根据离心空压机内气体流动特性，通过预测的总熵增和损失建立了不同高度下的空压机MAP图。其次，基于无刷直流电机反电势特征构建了高速空压机驱动电机模型，并将空压机模型与驱动电机模型结合至阴极空气供应系统模型中。最后，所提出的阴极供气系统FFM控制可实现PEMFC在0～3 km宽工况条件下运行，满足不同飞行状态下的功率需求，保证在无人机飞行状态和高度发生改变时，PEMFC过氧比和阴极压力能够在短时间内跟踪上给定值，减小由气压变化以及供气不足等对燃料电池寿命和耐久性的影响。

1 无人机用PEMFC阴极供气系统建模

针对无人机飞行高度的变化，建立了高速离心空压机的数学模型，并给出了不同高度下的空压机特性分析，根据能量守恒和质量连续方程，对供应歧管、燃料电池电堆和返回歧管进行了动态建模，具体PEMFC供气系统框图如图1所示。图中：Wcp为空压机流量；Wsm.out为供应歧管出口流量；Wca.out为阴极出口流量；Wrm.out为返回歧管出口流量;Wan.in和Wan.out分别为阳极入口和出口流量。

图1 PEMFC系统框图

1.1 变高度下空压机与驱动电机建模

目前针对PEMFC阴极供气系统中采用的空压机模型，主要是通过神经网络等数据拟合方法得到，其建模过程存在数据量大、处理难度高等缺点，建立的空压机模型大多只适用于地面，未考虑环境变化对其带来的影响。因此，建立变高度下空压机及驱动电机模型并进行控制，对燃料电池系统在中低空环境下的实际应用具有重要意义。

1.1.1 环境模型

空压机入口气体特性随着高度的变化而改变，而入口气体的温度Th、压力Ph、空气密度ρh等均会直接影响到空压机出口气压Pcp的大小。因此，研究不同高度下的气体特性对变高度下的空压机建模十分重要。在海拔高度小于11 km时，Th及Ph与海拔高度h有如下关系[29]:

Th=T0+Lt(h-h0)

(1)

(2)

式中：T0=293 K;P0=101 325 Pa;h0=0 m;R为理想气体常数；g0为重力加速度常数；Ma为空气的摩尔质量；Lt为温度变化率。

空压机入口空气密度的大小直接影响到空压机的能量转换效率。水平面处的空气密度约为1.29 kg/m3，海拔高度h处的空气密度ρh可表示为

(3)

式中：Z为压缩系数。

1.1.2 变高度下空压机特性

与容积式空压机不同，离心空压机的输出流量与压力间存在强耦合关系。假设气体压缩为等熵压缩，考虑能量传递对空压机性能的影响，变高度下空压机的工作特性可表示为

Δht(ωcp,Wcp)=Δhs(ωcp,Wcp)+Δhi(ωcp,Wcp)+

Δhf(ωcp,Wcp)+Δhother(ωcp,Wcp)

(4)

(5)

(6)

式中：Δht为焓的总增加量；Δhs为实际焓增量；Δhi、Δhf分别为气体在叶片入口处和扩散器处因入射损失、摩擦损失引起的熵增；Δhother为在压缩过程中由其他损失引起的熵增，这里假设为总熵增的8%;ωcp为转轴的旋转速度；Pcp、Tcp.out分别为空压机出口的气体压力和温度；ψ为空气机压比；cp为定压比热容；cv为定容比热容；γ=cp/cv为比热容比,约为1.4。

式(4)中空压机出口流量Wcp可根据供应歧管气压Psm与空压机压比ψ得到：

(7)

式中：A1为空压机叶轮眼面积;Lc为空压机气体传输管道长度。

滞止焓的表达式为

(8)

(9)

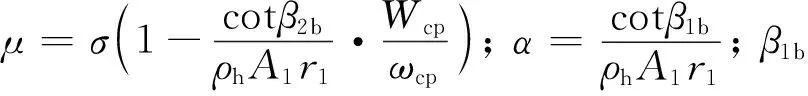
压缩过程中的摩擦损失与雷诺数Re相关，不同条件下雷诺数的变化对空压机的输出性能会产生较大影响。在变高度条件下，摩擦损失Δhf与Re的关系如式(10)～式(12)所示：

Δhf=Δhfi+Δhfd

(10)

(11)

(12)

式中：Δhfi和Δhfd分别为在叶轮和扩散器处的摩擦损失；li和ld分别为平均叶轮管道长度、平均扩散器管道长度；Di和Dd分别为叶轮处平均液压管道直径、扩散器处的平均液压管道直径；α2b为相对于切线方向的扩压器进口角；A1为流通面积；f为平均雷诺数的摩擦系数,

f=0.316 4(Re)-0.25

(13)

(14)

其中：D2为叶轮尖端直径；u2为叶轮叶片出口的圆周速度；μ2为叶轮出口气体温度为T2时的动力黏度，假设为常数20.5×10-6kg·s/m2;ρ2为叶轮出口气体密度。

基于式(1)～式(14)，给出了空压机在0、2、3 km处的MAP图，分别反映了在相应高度下空压机转速、质量流量以及出口气压间的动态关系，如图2所示。其中，通过实验测量获得的空压机地面数据在图2(a)中给出。

由图2可看出，所建立的空压机特性模型与实验测量数据有较好的吻合度，且随着高度的增加，空压机输出气体的质量流量及压力范围逐渐变窄，空压机正常工作范围缩小。在海拔0、2、3 km 高度下，最大输出质量流量分别为0.024 2、0.019 5、0.017 5 kg/s，相应的最大输出压力分别为1.732×105、1.391×105、1.251×105Pa。

图2 不同高度下空压机MAP图

1.1.3 空压机驱动电机建模

空压机由每一时刻两两导通，三相六状态运行的无刷直流电机(BLDCM)驱动，如图3所示。

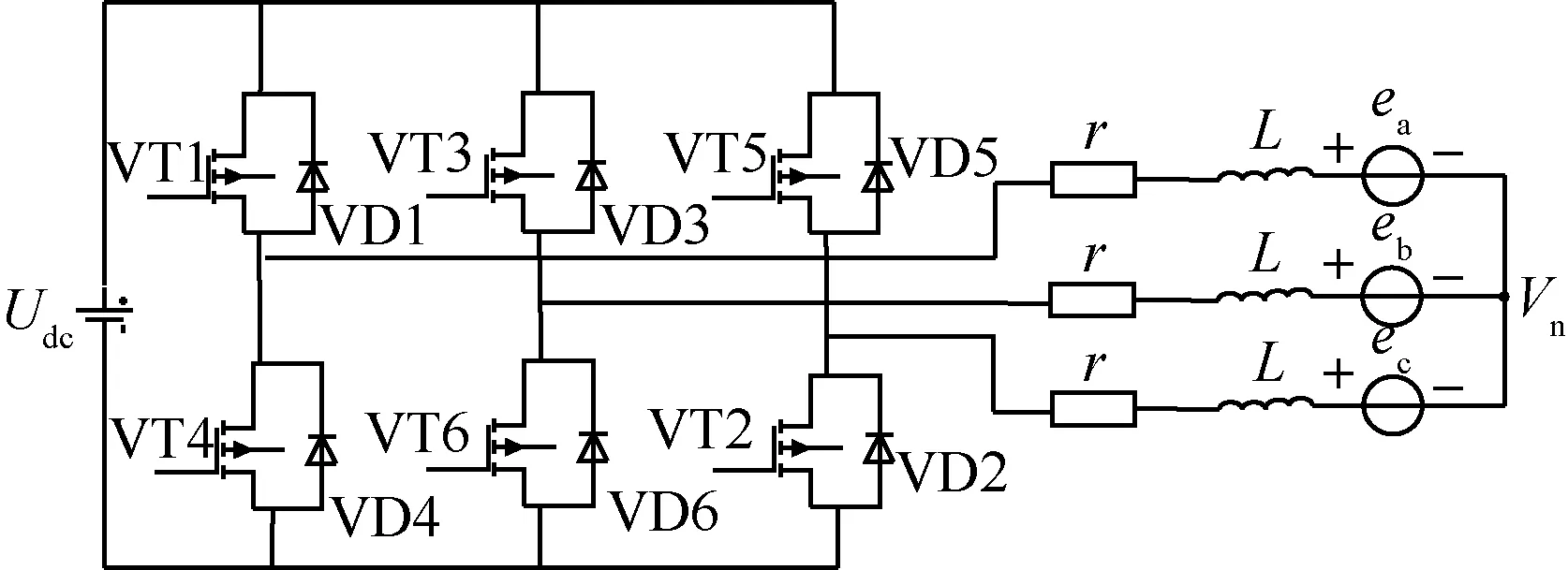
图3 无刷直流电机原理图

BLDCM三相电压平衡方程为

(15)

式中：ua、ub、uc和ia、ib、ic以及ea、eb、ec分别是相电压、相电流和各相的反电动势；r=ra=rb=rc为定子电阻；L为定子电感；Vn为电机三相绕组中性点的电压。采用星型连接，三相反电势和三相电流间存在以下关系：

|ea|=|eb|=|ec|=Cφωcp

(16)

ia+ib+ic=0

(17)

式中：Cφ为磁链。

BLDCM三相理想反电动势对应的电流波形、霍尔信号如图4所示。

图4 理想反电动势、电流及霍尔信号

BLDCM的动态特性方程为

(18)

(19)

(20)

式中：J为转动惯量；τcm为无刷直流电机产生的电磁转矩；τcp为空压机的负载转矩；ηcp为空压机的效率。

1.2 歧管动态建模

1.2.1 供应歧管建模

供应歧管入口流量为空压机的输出流量Wcp，供应歧管出口流量为Wsm.out，根据能量守恒和质量连续方程，供应歧管的压力表达式为[30]

(21)

式中：Ra为空气气体常数；Tcp.out为空压机出口气体温度；Vsm为供应歧管体积；Tcp.out与空压机压比和效率有关，即

(22)

式中：ηcp为空压机效率。

Wsm.out与Psm和阴极压力Pca有关，即

Wsm.out=Ksm.out(Psm-Pca)

(23)

1.2.2 返回歧管建模

返回歧管的压力与阴极出口流量Wca.out和返回歧管出口流量Wrm.out相关，表达式为

(24)

阴极出口流量的表达式为

Wca.out=Kca.out(Pca-Prm)

(25)

式中：Trm为返回歧管气体的温度，假设与燃料电池电堆温度Tst相同；Vrm为返回歧管体积；Kca.out为返回歧管的流量系数。

返回歧管出口流量Wrm.out是关于返回歧管压力Prm和末端环境气压Ph的函数：

(26)

式中：ADrm为返回歧管阀门的开口面积。

1.3 燃料电池电堆建模

1.3.1 阴极气压建模

阴极气压建模描述的是阴极内部气体的动态变化特性，其中，氧气和氮气是阴极流道中主要气体成分，氧气和氮气分压可根据气体的质量守恒和理想气体定律得到[31]:

(27)

(28)

Pca=PO2+PN2+Psat

(29)

式中：Vca为阴极体积；MO2和MN2分别为氧气和氮气的摩尔质量；WO2.in和WN2.in分别为阴极入口处氧气和氮气的质量流量；WO2.out和WN2.out分别为阴极出口处氧气和氮气的质量流量；WO2.react为阴极消耗氧气的质量流量；Psat为饱和水蒸汽压力。

1.3.2 燃料电池电堆电压建模

燃料电池电堆模型由N片燃料电池单体串联组成，电堆输出电压为[32-34]

Vst=NVfc=N(Enernst-Vact-Vohm-Vcon)

(30)

式中：Vfc为燃料电池单体输出电压；Enernst为能斯特电动势；Vact为活化损失过电势；Vohm为欧姆损失过电势；Vcon为浓差损失过电势。能斯特电动势以及3种损失过电势的表达式为

Enernst=1.229-8.5×10-4×(Tfc-298.15)+

(31)

Vact=V0+Va(1-e-c1j)

(32)

(33)

Vohm=j·Rohm

(34)

式中：Tfc为燃料电池工作温度，假设与燃料电池电堆温度Tst相同；V0为电流密度为零时的压降；Va与温度和氧气分压有关；Rohm为欧姆内阻；j和jmax分别为电流密度和最大电流密度；c1、c3均为常数；c2与饱和水蒸气压力和燃料电池工作温度有关，电堆各参数的取值及表达式见附录A。

2 控制器设计

PEMFC系统是一个具有非线性、强耦合性的多输入多输出系统，其系统效率和动态性能受到阴极供气系统的直接影响。本文的控制目标为基于所建PEMFC阴极供气系统模型，避免氧饥饿，并保持PEMFC系统的高工作效率。为使控制效果最优，本文提出了针对过氧比和阴极压力的双闭环控制，控制系统结构如图5所示。

如图5所示，阴极压力基于分数阶PIλDμ控制，通过调节返回歧管阀门开口面积来控制阴极压力保持在给定值，过氧比控制由分数阶PIλDμ控制外环和MPC控制内环组成，该控制策略简写为FFM。首字母F代表阴极压力分数阶控制，后者F代表过氧比分数阶控制，M代表电机转矩模型预测控制，并在图5中分别给出了模型和控制模块所对应的公式。

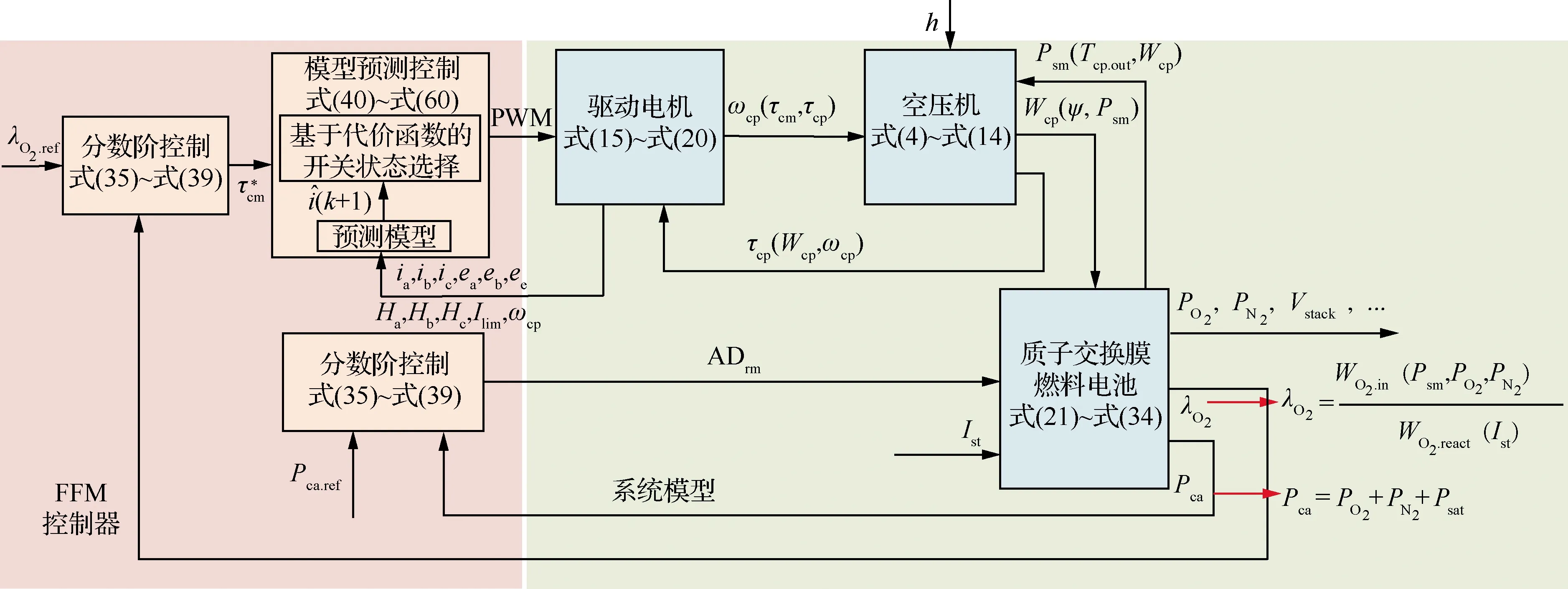
图5 FFM 控制系统框图

2.1 阴极压力与过氧比控制器设计

2.1.1 分数阶PIλDμ控制器

以阴极压力分数阶PIλDμ控制器为例，结构框图如图6所示。图中，分数阶PIλDμ控制器的时域表达式为

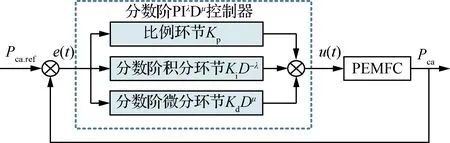
图6 阴极压力控制结构

u(t)=Kpe(t)+KiD-λe(t)+KdDμe(t)

(35)

式中：u(t)为返回歧管阀门开口面积；e(t)为阴极压力参考值与系统输出的差值ΔPca。

2.1.2 分数阶PIλDμ控制器设计

设计一个分数阶PIλDμ控制器需要确定5个参数：Kp、Ki、Kd、λ和μ。为使所设计的分数阶PIλDμ控制器控制效果最优，在传统参数整定方法——主导极值点法的基础上，采用了一种新的参数整定方法——极点阶数搜索法。并以阴极压力控制为例，给出了基于极点阶数搜索法的分数阶PIλDμ控制器设计的具体步骤，并以时间乘绝对误差积分准则(ITAE)作为控制参数整定的性能指标。

步骤1估计比例增益Kp。

Kp的估计值可根据系统稳态误差ΔPca与理想给定值Pca.ref之比Et得到：

Kp=[100/(Et0Pca.ref)-1]a0

(36)

式中：a0为被控系统传递函数中的系数，防止Kp过大导致系统不稳定。Et0和Et存在以下关系：

(37)

步骤2确定极点S1,2。

系统极点主要对系统的闭环响应过程产生影响，当闭环系统主要受到一对主导极点的影响时，该对主导极点用以下形式给出[35]

(38)

式中：σ为极点稳定度;ξ为阻尼比。

当步骤1和步骤2中的Kp和S1,2确定后，采用阶数搜索方法来确定控制器中其余的4个参数:Ki、Kd、λ和μ。

步骤3确定积分阶次λ和微分阶次μ的第i(1≤i≤3)次搜索范围。

当i=1时，μ∈[0,2.0],λ∈[0,1.5]，搜索步长Δ1=0.1。

当i>1时，μ∈[max(Δi,μi-1-2Δi-1),μi-1+2Δi-1],λ∈[max(Δi,λi-1-2Δi-1),λi-1+2Δi-1]，搜索步长Δi=Δi-1/10。

步骤4确定i次搜索时的Kd、μ、Ki、λ。

将步骤1～步骤4中得到的Kp、S1,2和λ、μ的第i次搜索范围中的值依次代入特征方程中，并令其等于零，即可解得每组的控制参数Kd、μ,Ki、λ。根据系统性能指标(ITAE)来判定所得参数是否满足要求，若有一组参数满足指标要求，则结束搜索；若均不满足指标要求，则记录第i次搜索中最接近指标要求的μi和λi，使i=i+1，若i≤3则返回步骤3，若i>3则进行步骤5。

步骤5重新搜索5个参数。

若系统阶跃响应时的ITAE较大或调节时间T较长，则适当增大Kp，若系统阶跃响应的超调较大，则适当减小Kp，并重复执行步骤2～步骤4。具体的分数阶PIλDμ控制器设计流程如图7所示。

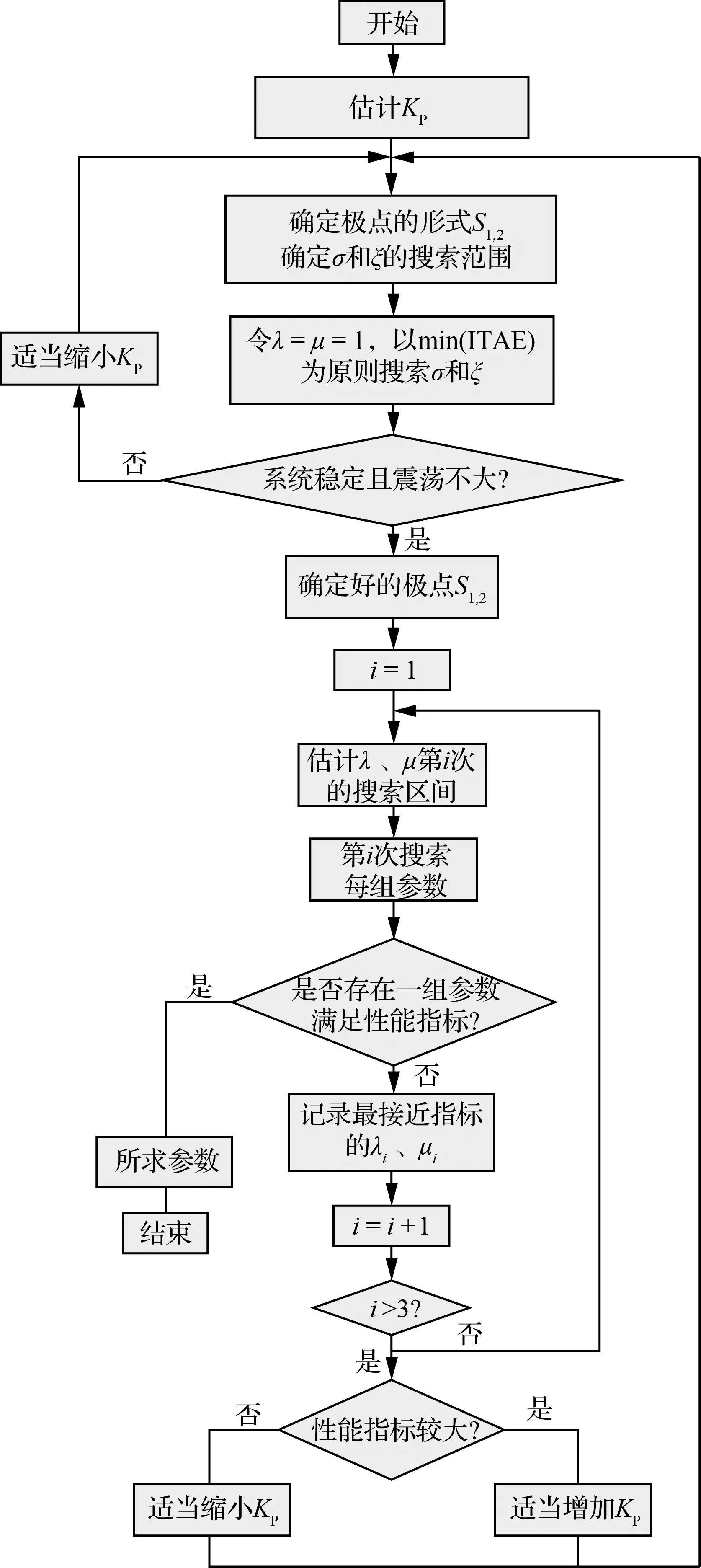
图7 最优分数阶PIλDμ控制设计流程

文中选用ITAE优化准则的数学定义为

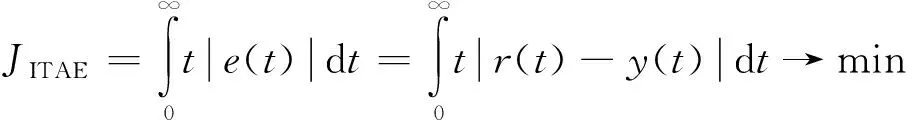
(39)

式中：r(t)为闭环系统给定参考值；y(t)为闭环系统实际输出值。

2.2 电机驱动转矩控制器设计

2.2.1 电流预测模型建立

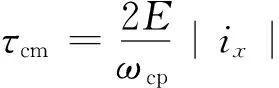
当无刷直流处于换相时刻时，a、b、c相电压与直流母线电压的关系为

(40)

δ值与非换相相、续流电流大小以及导通相开关管开通关断有关，假设δx、δy、δz分别对应非换相相、续流电流相和导通相。在电机运行6状态下，非换相相δx、续流电流相δy和导通相δz因运行状态的不同，均可表示电机a、b、c三相中的任意一相。

因此，状态变量为相电流ia、ib、ic以及转速ωcp，控制变量为开关状态δa、δb、δc以及转矩τcm。

上管调制：当由c+b-转换为a+b-拍时(即VT5、VT6导通→VT1、VT6导通)，

ea=-eb=E

(41)

1)ic≠0A(即c相电流续流)，若VT1导通，则δz=δa=1、δx=δb=0、δy=δc=0。若VT1关断，则δz=δa=0、δx=δb=0、δy=δc=0。使用基尔霍夫定律得到当VT1处于导通和关断状态时a、b、c相电压方程为

VT1导通时:

(42)

VT1关断时:

(43)

将式(15)、式(40)～式(43)离散化得到

(44)

(45)

式中：ib(k+1)、ib(k)分别为非换相相k+1时刻和k时刻电流值；Ts为采样周期；on和off分别表示换相开关管开通及关断状态。

2)ic=0 A(即c相电流续流结束)，若VT1导通，则δz=δa=1、δx=δb=0、δy=δc=0。若VT1关断，则δz=δa=0、δx=δb=0、δy=δc=0。使用基尔霍夫定律得到当VT1处于导通和关断状态时a、b相电压方程为

VT1导通时:

(46)

VT1关断时:

(47)

将式(15)、式(41)、式(46)、式(47)离散化后得到

(48)

(49)

下管调制：当由a+b-转换为a+c-拍时(即VT1、VT6导通→VT1、VT2导通)，

ea=-ec=E

(50)

1)ib≠0A(即b相电流续流)，若VT2导通，则δx=δa=1、δy=δb=1、δz=δc=0。若VT2关断，则δx=δa=1、δy=δb=1、δz=δc=1。使用基尔霍夫定律分别得到当VT2处于导通和关断状态时a、b、c相电压方程为

VT2导通时:

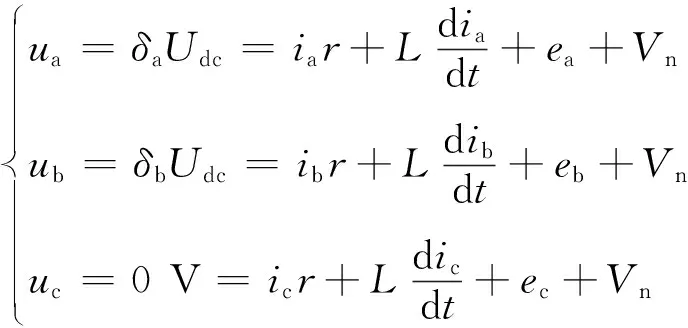
(51)

VT2关断时:

(52)

将式(15)、式(40)、式(50)～式(52)离散化得到

(53)

(54)

2)ib=0A(即b相电流续流结束)，若VT2导通，则δx=δa=1、δy=δb=0、δz=δc=0。若VT2关断，则δx=δa=1、δy=δb=0、δz=δc=1。使用基尔霍夫定律得到当VT2处于导通和关断状态时a、c相电压方程为

VT2导通时:

(55)

VT2关断时:

(56)

将式(15)、式(50)、式(55)、式(56)离散化后得到：

(57)

(58)

基于包含逆变器数学模型的预测模型，有限集模型预测控制分别考虑了在导通相电流续流(iy≠0 A)和续流结束(iy=0 A)两种情况下，导通相功率开关管分别开通或者关断状态时，电机非换相相未来时刻电流有4种可能预测值。同时，当电机在ab、ac、bc、ba、ca、cb相导通的6种不同运行条件下，下一时刻预测值也是不同的，故每个周期共有24种有限情况。

2.2.2 滚动优化

根据2.2.1节建立的电流预测模型，为减小非换相相电流波动，最小化非换相相电流以及对电流幅值进行约束，设计代价函数：

(59)

(60)

取min={J1,J2}，决定下一时刻导通相开关管的on或off状态。

因无刷直流电机的极对数p=1，运行频率为0～4 667 Hz。为保证模型与控制策略的可靠性，仿真速度应大于50倍电机频率，故文中设置模型预测的采样频率为250 kHz，步长Ts=4×10-6。文中采用的模型预测为一步预测，即预测时域为1。

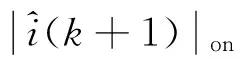
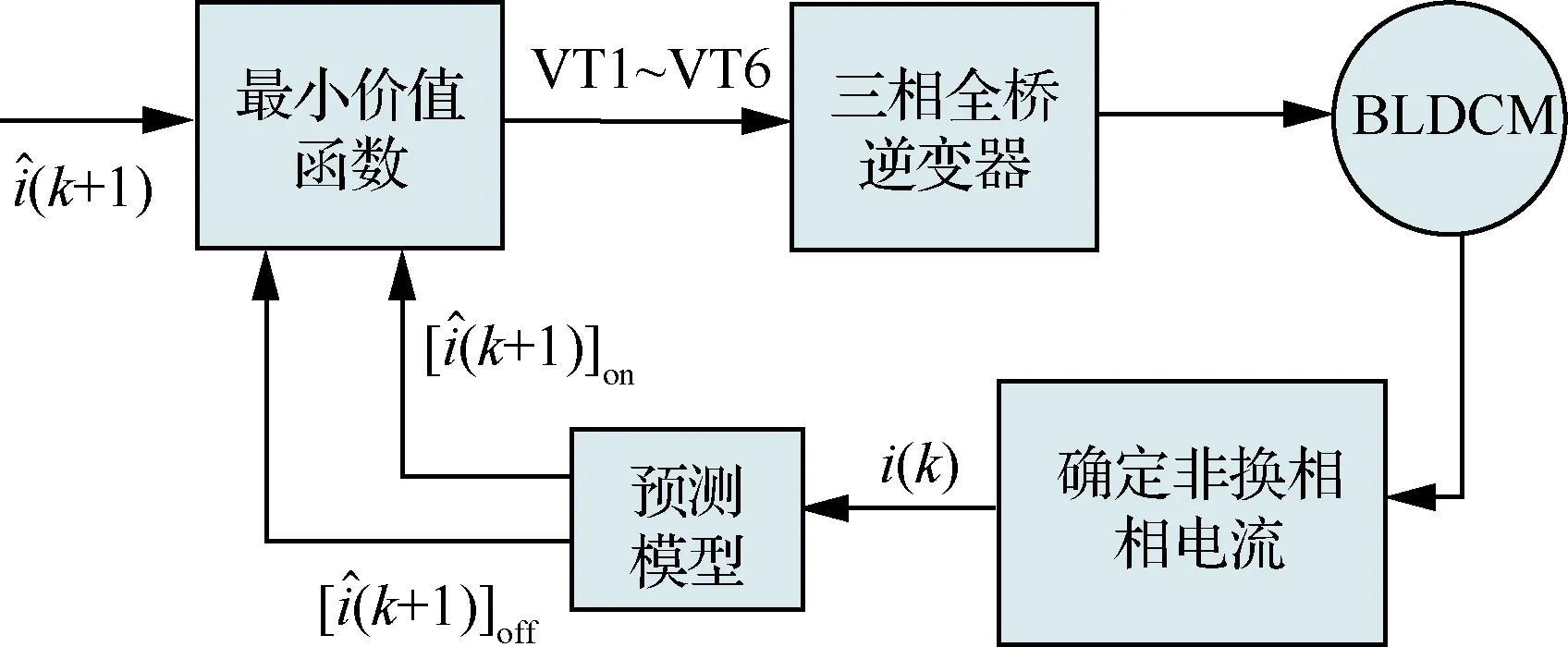
图8 模型预测控制系统框图

3 仿真结果分析

为验证建立的系统模型和提出的FFM控制方法，基于无人机飞行任务模拟过程，对控制的快速动态响应特性和抑制转矩脉动特性在MATLAB/Simulink上进行了仿真分析。同时，与PPM控制(首字母P代表阴极压力PID控制、后者P代表过氧比PID控制、M代表电机转矩MPC控制)和PPP控制(首字母P代表阴极压力PID控制、中间P代表过氧比PID控制、后者P代表电机转矩PID控制)进行了对比。燃料电池、空压机及驱动电机和3种控制方法的详细参数请见附录A。

无人机飞行任务模拟过程如图9所示。其中，阴极压力与过氧比给定值的设置依据与不同高度下空压机的工作特性有关，在20 s后，巡航负载电流小，空压机输入流量低，导致空压机实际工作点在喘振线左侧，为保证空压机始终工作在正常工作区域，将过氧比参考值提高至5，同时将阴极压力参考值降至地面气压1 atm(1 atm=101 325 Pa)。

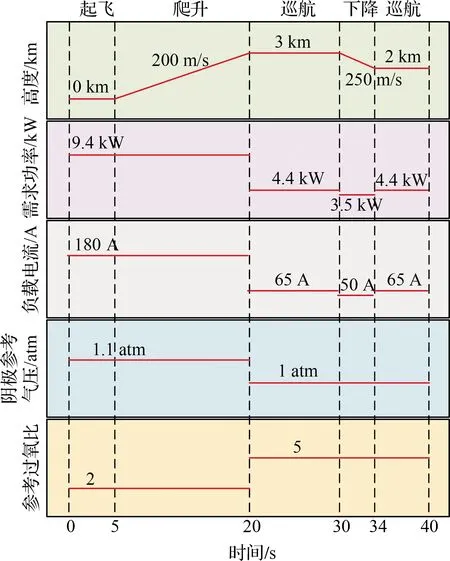
图9 无人机飞行任务模拟

3.1 阴极压力闭环控制

3种控制下阴极压力的控制效果如图10所示，由图可见，3种控制方法均可实现将阴极压力控制在参考值附近，且稳态误差较小可忽略。在20 s参考值发生改变时，FFM调节时间相比PPM减小了0.5 s,仅为PPM调节时间的37%，PPM和PPP两种控制下的阴极气压无明显差异；在30 s和34 s时，因受空压机流量控制的耦合影响，阴极气压分别有一个短暂减小和短暂增大的过程，但阴极气压减小和增大的幅度及响应时间都较小，可忽略，因此图中未给出这两个时间的局部放大图。

图10 阴极气压控制效果

调节返回气管阀门开口面积的大小是实现阴极气压控制的有效途径之一，阀门开口面积越大，阴极气压越低。在20 s时，因阴极气压参考值减小，导致阀门开口面积突然增加，以期在短时间内降低阴极气压跟踪上给定值，阀门开口面积的变化情况如图11所示。

3.2 过氧比闭环控制

3种控制方法下过氧比的控制效果如图12所示。其中图12(a)是过氧比的整体控制效果，可见在无人机飞行状态发生改变时，3种控制方法均可将过氧比稳定在给定值附近，FFM相比PPM和PPP，在调节时间上具有明显的优势，而3种控制方法的超调量和稳态误差均差异不大。

图12(b)为无人机飞行状态由爬升到3 km 巡航时的局部放大图，此时无人机需求功率急剧减小，且因3 km处空压机特性的限制，需对过氧比做出相应的改变。由图可见，FFM控制的过氧比可以在较短的时间内跟踪上给定值，且相比PPM和PPP分别减少了75%和80%的调节时间，具体调节时间如表1所示。

图12(c)为无人机飞行状态由3 km巡航到下降时的局部放大图，此时无人机需求功率继续减小。由表1可知，FFM在调节时间上同样具有最优的控制效果，相比于PPM，其调节时间减小了60%，PPM和PPP的控制效果无明显差异。

图12(d)为无人机飞行状态由下降到2 km 巡航时的局部放大图，此时无人机需求功率增加，3种控制策略的调节时间如表1所示，FFM控制的调节时间仅为PPM控制的28%，为PPP控制的50%。

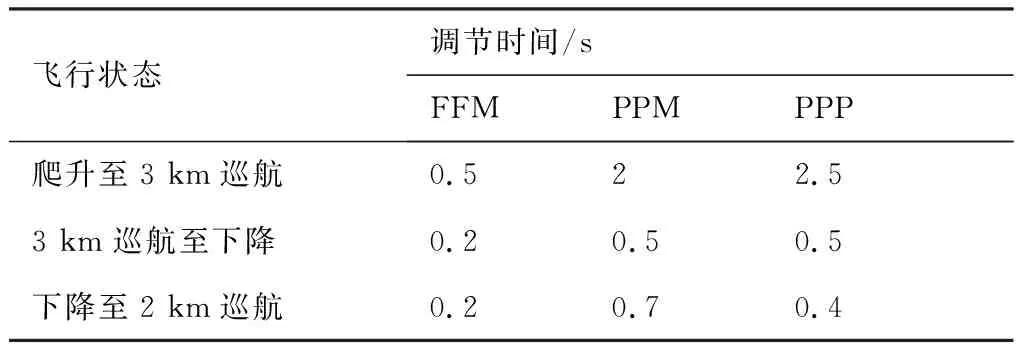
表1 3种控制方法过氧比控制的调节时间

过氧比定义为进入阴极的氧气流量与反应消耗氧气流量的比值，因此，过氧比的控制与空压机的流量紧密相关，图13给出了空压机流量的控制效果。

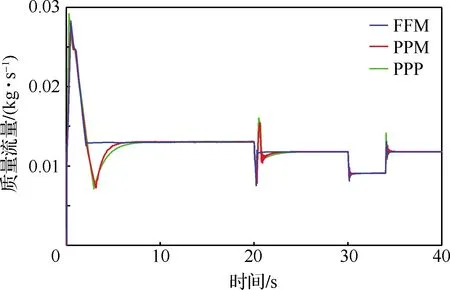
图13 空压机流量控制效果

电机驱动转矩的脉动会导致其运行转速的不稳定，严重时更会造成电机的损坏。本文为减小转矩脉动对电机的损害，提出了对转矩的MPC控制。基于FFM、PPM和PPP这3种控制下的电机驱动转矩如图14所示，由图可见，FFM和PPM控制下的电机转矩特性无明显区别，但相比PPP，转矩脉动减小了接近50%，有效降低了转矩脉动对驱动电机带来的损害。

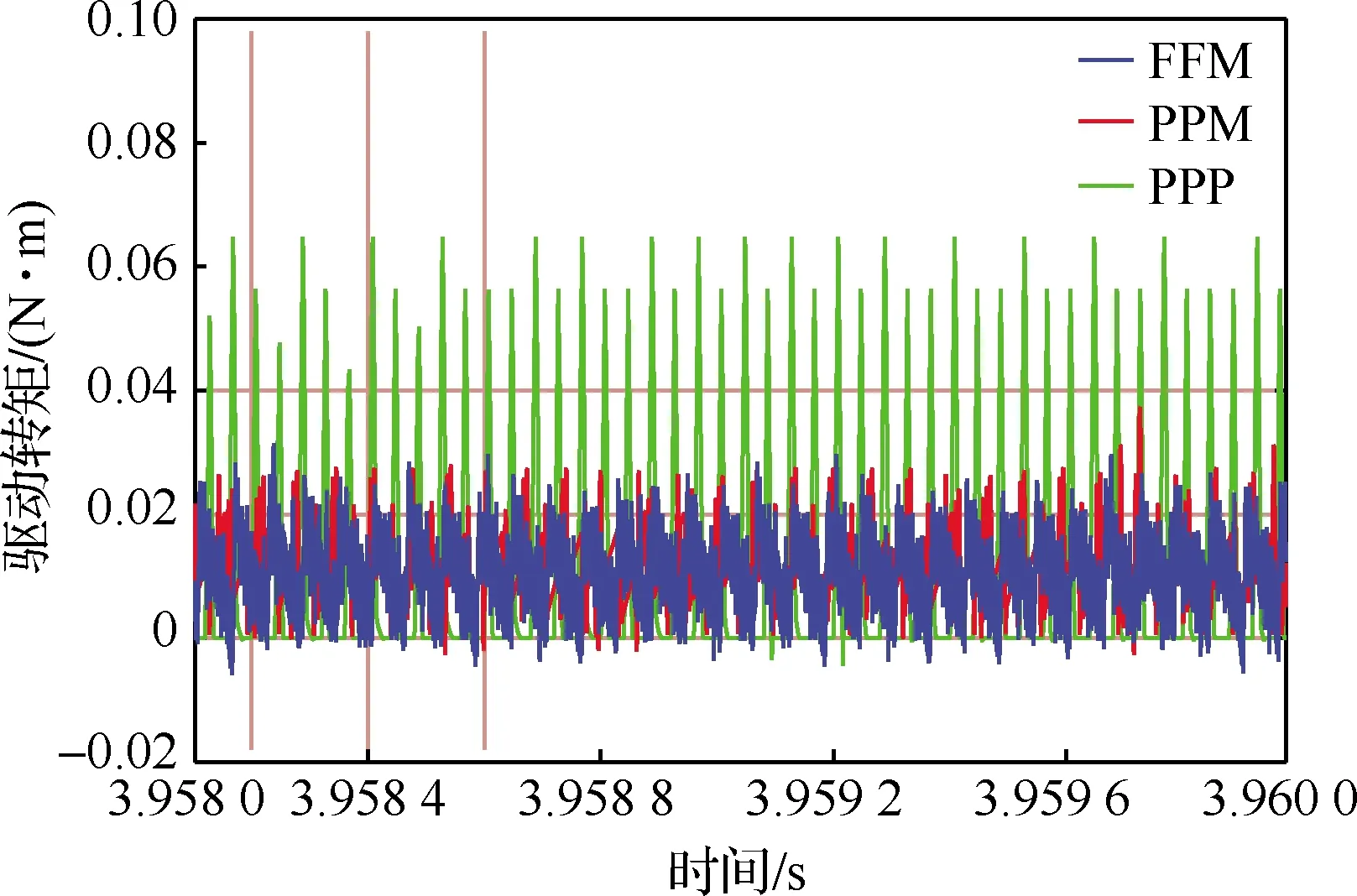
图14 驱动转矩控制

图15为FFM、PPP和PPM控制下的a相电压电流，对比可知，FFM和PPM控制下的a相电流脉动，仅为PPP控制的50%左右。因此，通过对图14和图15的对比分析可知，所提出的电机转矩MPC控制算法可有效降低转矩的脉动。

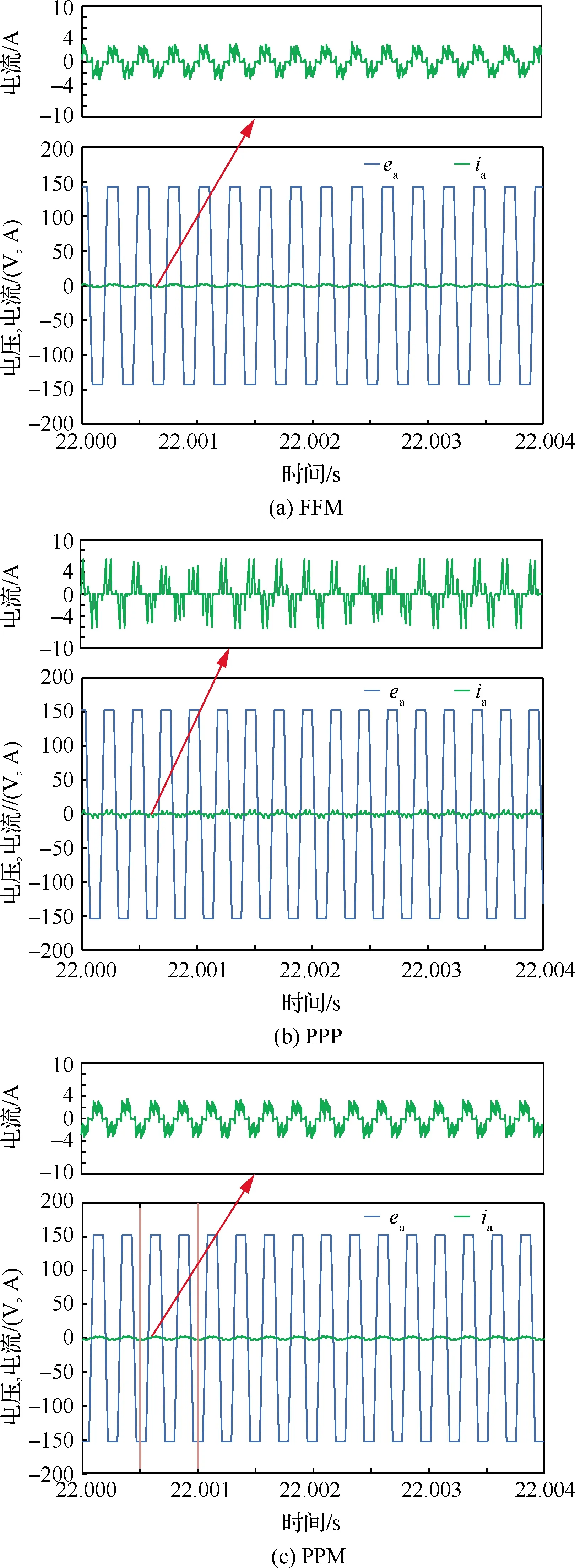
图15 3种控制方法下的a相电压、电流

文中无人机动力系统包含锂电池和PEMFC两种能源装置，锂电池仅用于启动时空压机的供电，PEMFC作为能源装置为不同飞行状态下的无人机提供需求功率，PEMFC系统输出功率的大小与无人机飞行状态紧密相关。图16和图17分别给出了3种控制策略下电堆电压和功率的控制效果，由图可见，无人机起飞及爬升阶段、巡航阶段和下降阶段电堆输出功率分别为9.4、4.4、3.5 kW，电堆电压相应为52、67、72 V，可满足图9中无人机在起飞和爬升阶段的大功率需求。

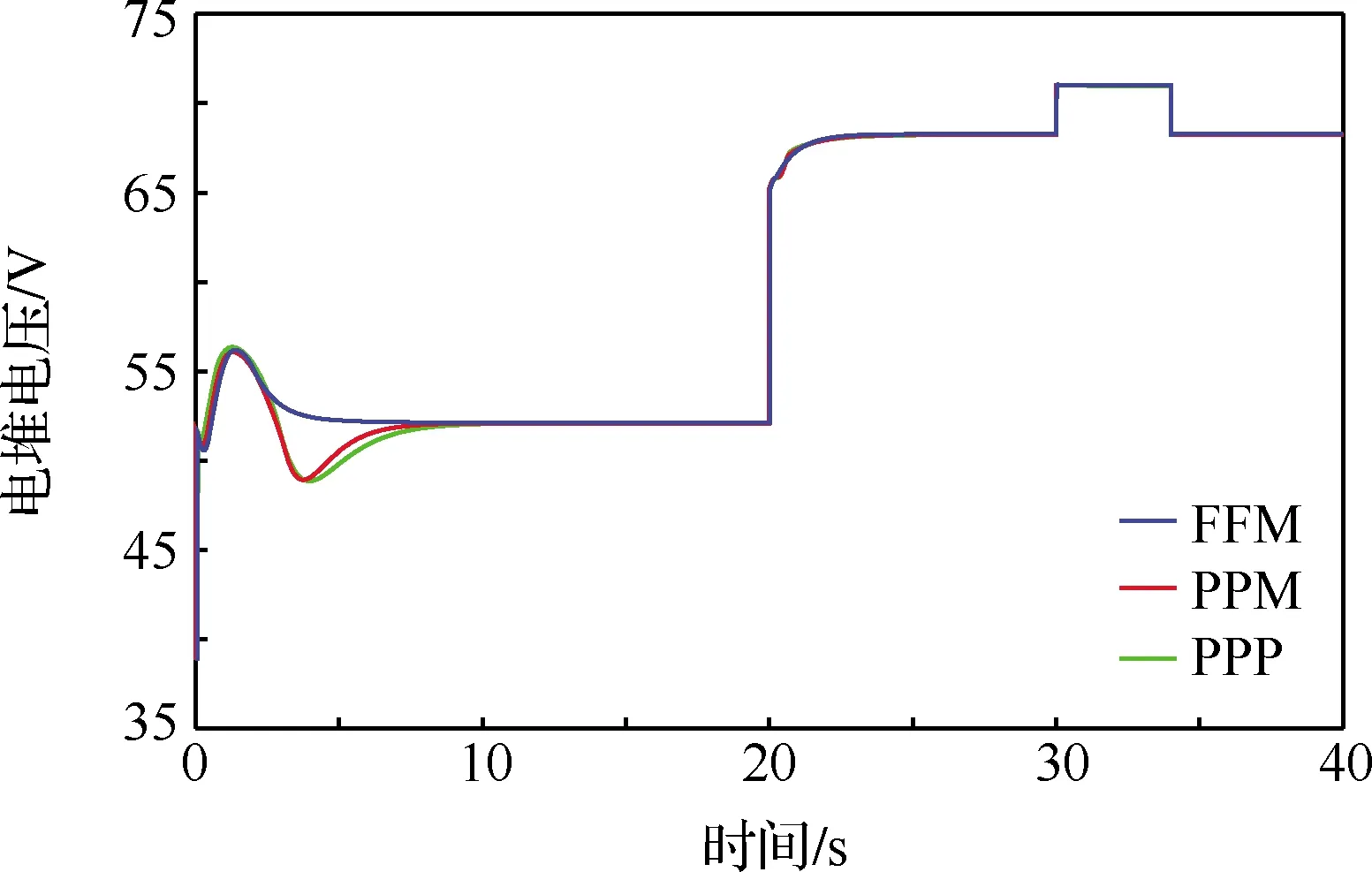
图16 电堆输出电压

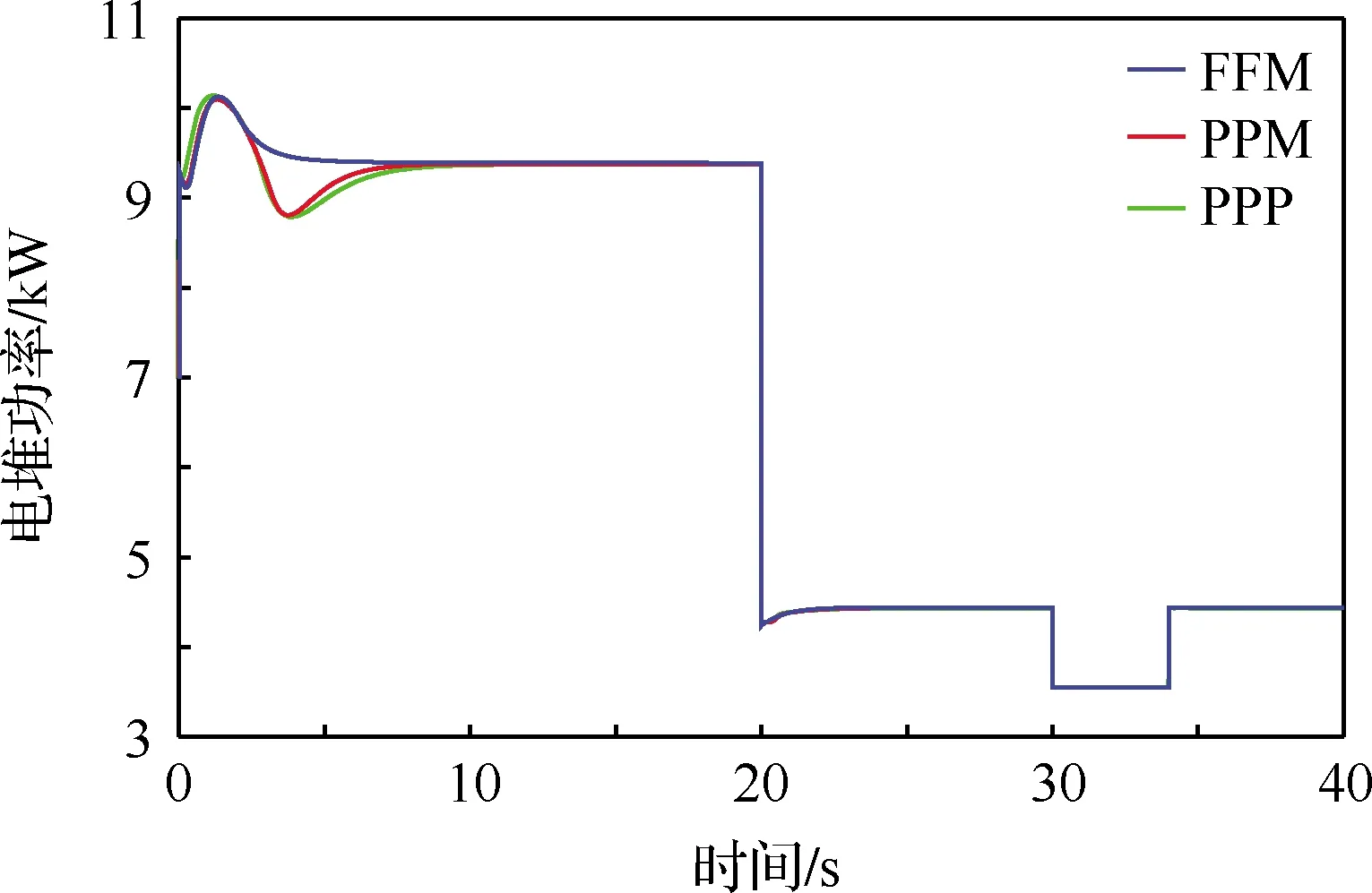
图17 电堆输出功率控制效果

4 结 论

1)针对无人机用燃料电池在不同飞行高度下面临的环境差异，考虑空压机入口处气体的温度、压力、密度以及雷诺数等影响，构建了跨高度离心式空压机模型、分析了不同高度下的空压机特性MAP图，在所建空压机模型的基础上完成了跨高度燃料电池阴极供气系统建模及控制方法的研究。

2)基于无刷直流反电势特征构建了高速离心式空压机驱动电机模型，同时针对电机驱动转矩采用了有限集模型预测控制，并通过仿真验证了MPC控制方法可有效降低驱动转矩脉动。

3)所提出的FFM控制能够根据阴极气压及过氧比的变化，及时调整阴极背压阀开口面积和电机驱动转矩，进而通过电机驱动转矩调节空压机转速，以在短时间内跟踪上过氧比及阴极压力参考量，具有可调参数范围大、动态响应速度快、电机转矩脉动小等特点。所提出的FFM控制可实现燃料电池在0～3 km宽工况条件下运行，并满足无人机不同飞行状态下的功率需求。

附录A

空压机及驱动电机参数见表A1。

表A1 空压机及驱动电机参数

Table A1 Parameters of air compressor and brushless motor

符号定义单位数值ψ地面最大压力比1.7Wcp地面最大流量g/s24ηsmax地面最大等熵效率70m重量g600Pe额定功率W1 000p极对数1J转动惯量kg·m25.5×10-7Cϕ磁链Wb6.6×10-3Ie额定相电流A2.7r定子电阻Ω0.9L定子电感μH160σ滑移因子0.875A1流通面积m27.9×10-5β1b叶片入口角度(°)28β2b转子叶片角度(°)80r1平均诱导半径m0.010 3

燃料电池参数见表A2。

表A2 燃料电池参数

Table A2 Fuel cell parameters

符号定义单位数值N单电池个数100γ空气比热容比1.4Tst电池堆温度K313.15Tatm环境温度K298.15Vsm供应岐管体积m30.01Vca阴极体积m30.01Vrm返回岐管体积m30.005Mv水蒸气摩尔质量kg/mol0.018MN2氮气摩尔质量kg/mol0.028MO2氧气摩尔质量kg/mol0.032Ma空气摩尔质量kg/mol0.029Φatm环境空气的相对湿度0.5Ksm.out供应管道孔口常数kg/(s·Pa)2×10-5Kca.ou阴极出口常数kg/(s·Pa)1×10-5mv.ca.max阴极侧水蒸气的最大质量kg/mol0.0018yO2.atm氧气摩尔分数0.21yN2.atm氮气摩尔分数0.79

3种控制方法参数见表A3。

表A3 3种控制方法参数

Table A3 Parameters of three control methods

方法阴极压力控制KpKiKdλμFFM0.0041×10-61×10-40.60.9PPM0.002 51×10-61×10-4PPP0.002 51×10-61×10-4方法过氧比控制KpKiKdλμFFM20.11×10-80.50.01PPM15200PPP25200方法电机转矩控制KpKiKd预测时域仿真步长FFM14×10-6PPM14×10-6PPP0.90.851×10-4

燃料电池电堆参数为

V0=0.279-8.5×10-4(Tfc-298.15)+

Va=(-1.618×10-5Tfc+1.618×10-2)·

(-5.8×10-4Tfc+0.5736)

c1=10,c3=2,jmax=2.2 A/cm2

b11=0.051 39,b12=0.003 26,b2=350,

λm=14