结构参数对拦阻钩碰撞反弹动力学影响分析

彭一明，张钊，魏小辉,*，聂宏，谢朋朋

1.南京航空航天大学 机械结构力学及控制国家重点实验室，南京 210016 2.南京航空航天大学 飞行器先进设计技术国防重点学科实验室，南京 210016 3.上海卫星装备研究所，上海 200240

舰载机的着舰与陆基飞机的着陆存在很多不同点，最为显著的区别就是舰载机安装有拦阻钩，其功能是在飞机进入着舰区域后能够顺利地与甲板上的拦阻悬索啮合，将拦阻力传递到机身上，以使飞机快速拦停[1]。

舰载机在拦阻钩挂索之前，一般情况是拦阻钩先与甲板碰撞，并在拦阻钩纵向阻尼器的作用下发生有限高度的弹跳。由于舰载机着舰时下沉速度较大，这就导致拦阻钩与甲板碰撞将会以较大的初始角速度上转回弹，若无法迅速有效地实施控制，拦阻钩可能会上转过高超过拦阻索，更为严重时会与飞机尾部碰撞，造成着舰事故[2]。拦阻钩成功套索的必要条件是第1次反弹高度不超过100 mm、长度不超过6.1 m[3]。因此，为提高拦阻钩挂索成功率，研究如何抑制拦阻钩反弹并对拦阻钩碰撞反弹动力学进行深入的分析尤为重要。

国外对于拦阻钩动力学的研究已经较为成熟，由于保密的原因，公布的文献较少且陈旧。例如，Thomlinson[4]对飞机在对称面内对拦阻钩与甲板的碰撞和反弹进行了详细描述，通过分析构建几何连接关系建立起机身与拦阻钩之间的运动学方程；Jones[5]分析了拦阻过程中拦阻钩钩载峰值的主要影响因素，并基于拦阻系统的数据统计得到了拦阻力拟合公式和曲线；全美工程公司公布的一份报告[6]对拦阻钩碰撞悬索支撑物的情况进行了分析。

国内学者对拦阻钩碰撞动力学进行了大量理论研究[7-11]，系统分析了拦阻钩初次碰撞甲板后反弹的成因，在着舰对称面内建立了拦阻钩碰撞反弹模型，考虑甲板突起物[9]、摩擦力[7]、纵向缓冲器[8,11]等因素对碰撞反弹动力学的影响。国内学者还进行了拦阻钩碰撞反弹相关的试验研究，杨全伟[12]提出了拦阻钩载荷实测方法，实测了拦阻钩碰撞时的载荷；彭一明和聂宏[1]通过碰撞反弹试验修正了含涂层甲板的恢复系数；豆清波等[13]提出了拦阻钩系统冲击性能试验方法，进行了拦阻钩系统垂向冲击试验。这些研究的对象都是某一具体型号的拦阻钩，主要分析或测试拦阻钩碰撞反弹的相关性能，而针对新型舰载机拦阻钩设计初期技术人员关心的拦阻钩尺寸、质量、缓冲器安装尺寸、缓冲器结构参数的研究鲜有公开。

为完善拦阻钩装置设计体系，本文基于刚体碰撞动力学理论建立了拦阻钩撞击甲板反弹动力学模型，通过拦阻钩碰撞反弹试验对碰撞模型的参数进行了修正，并基于该模型分析了缓冲器安装形式、拦阻钩重心位置、缓冲器结构参数对碰撞反弹的影响，并基于双结构参数对弹跳性能的影响进行了设计优化。

1 拦阻钩碰撞反弹动力学模型

1.1 模型基本假设

在舰载飞机着舰过程中，拦阻钩钩头与甲板会在短时间内发生极为复杂的碰撞并反弹[14]。碰撞期间系统受到约束限制，在碰撞结束后约束消失，属于非持久碰撞[15]。根据舰载飞机着舰的基本特点，作出如下合理假设：① 将拦阻钩视为一根刚性杆，可在飞机对称面内绕机身铰接点转动；② 钩头与甲板的刚度可视作极大；③ 钩头与甲板的接触面平整，无凸起物；④ 碰撞过程中摩擦力远比碰撞力小，可以忽略。

1.2 拦阻钩与甲板碰撞模型

图1为拦阻钩与甲板碰撞示意图，XgOYg为地面坐标系;B点为拦阻钩与机身铰接点;A点为拦阻钩与甲板接触点，拦阻钩可绕点B在地面坐标系XgOYg内转动；拦阻钩简化为杆AB;C为拦阻钩的质心位置，BC段长l1,AC段长d2,总长为l;v为飞机的下滑速度;αl为飞机下滑轨迹角;β为甲板角;θ为拦阻钩轴线与竖直方向的夹角;ω为碰撞时刻反弹角速度[8],IBy为B点y方向的冲量分量;IBx为B点x方向的冲量分量;IA为A点冲量。

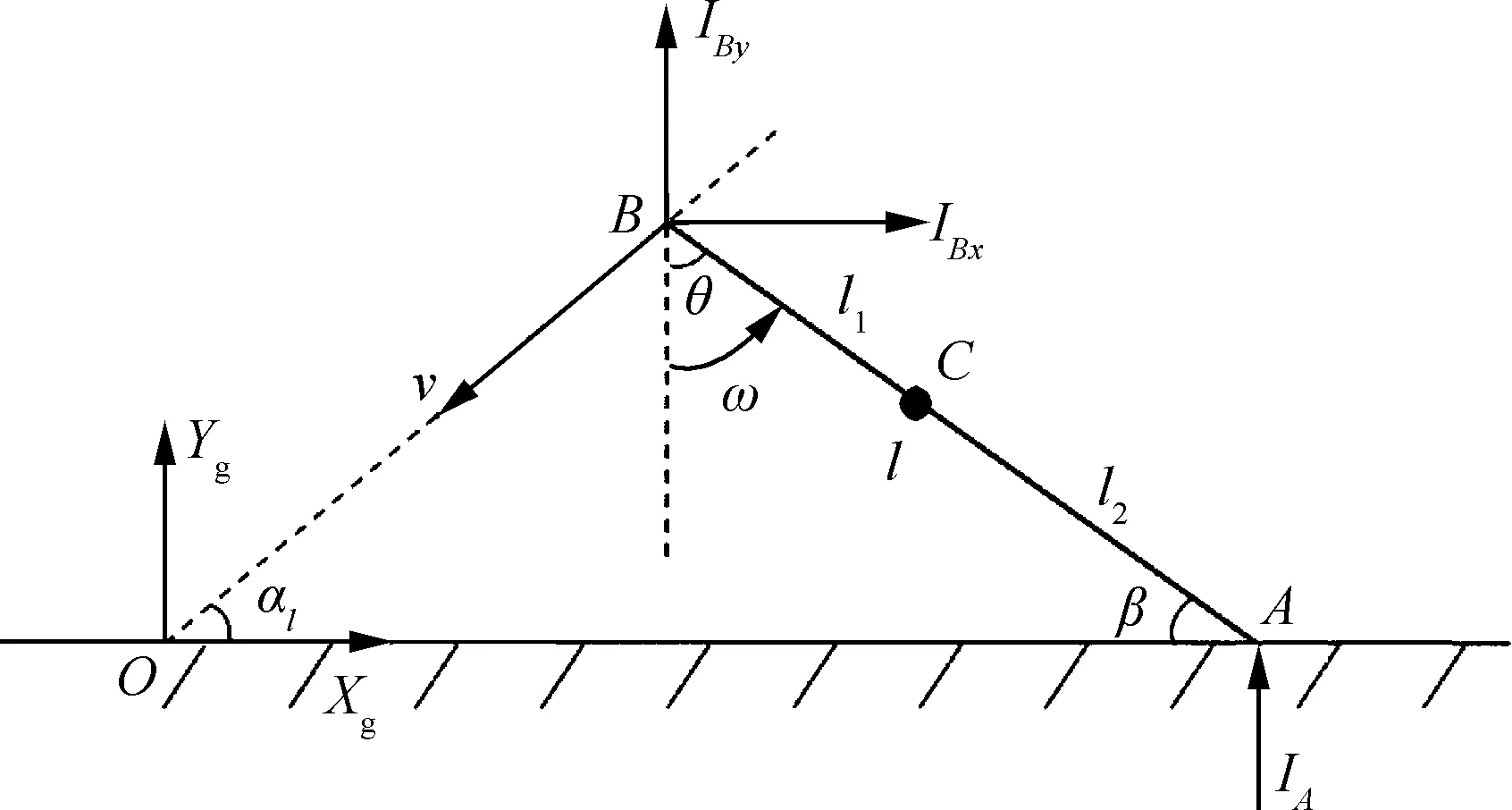
图1 拦阻钩与甲板碰撞示意图

在不考虑航母甲板运动时，碰撞恢复系数与钩头点A碰撞前后速度有关[16-18]。设碰撞恢复系数为e，则有

(1)

式中:v、u表示碰撞前后的速度，下标A表示A点，下标y表示在y方向上分量，下同。

在地面惯性系下拦阻钩碰撞动力学方程为

(2)

式中:m为拦阻钩质量;JC为拦阻钩绕质心的转动惯量;I为拦阻钩所受到的冲量。

根据运动学关系有

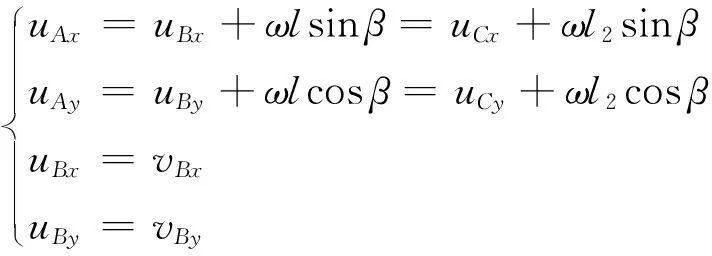
(3)

根据速度分量关系以及式(1)、式(3)可得

(4)

由式(2)～式(4)联合可得

(5)

1.3 拦阻钩反弹模型

拦阻钩反弹示意图如图2所示，AB为拦阻钩杆;PQ为拦阻钩缓冲器，P为两者铰接点，B、Q分别为钩杆与机身的连接点。各段长度以及角度如图所示,θ1为钩杆机身连接线与竖直方向的夹角;BQ段长a,BP段长b,PQ段长s;l1为质心距上铰接点距离;Fs为缓冲器作用力，作用于P点;mg为拦阻钩重力，作用于质心C点。

由图2中几何关系可得：

图2 拦阻钩反弹示意图

(6)

由动量矩定理可得

(7)

拦阻钩缓冲器与起落架缓冲器原理类似，其作用力Fs包括空气弹簧力Fa、油液阻尼力Fh和结构限制力Fl组成[1]，即

Fs=Fa+Fh+F1

(8)

不考虑油液的可压性和缓冲器腔体的体积变化时，空气弹簧力为

(9)

式中：Aa为压气面积；P0为缓冲器初始填充压强；V0为缓冲器初始冲压容积；n为气体多变指数；Patm为当地大气压强；sH为缓冲器行程。

本文中拦阻钩缓冲器阻尼器为单腔-常油孔-油气式，没有侧油孔，则油液阻尼力为

(10)

式中：ρoil为油液密度；Cd为主油腔油孔缩流系数；AZh为拦阻钩阻尼器有效压油面积；AZd为阻尼器油孔面积。

缓冲器结构限制力F1可表示为

(11)

式中：k1为结构限制力刚度系数；sH max为缓冲器最大行程。

最终可得钩头弹跳高度为

hA=lsinβ-lcosθ-vtsinαl

(12)

钩头航向位移为

xA=lcosβ-lsinθ+vtcosαl

(13)

式中:t为时间。

2 基于碰撞反弹试验的模型校验

拦阻钩与甲板撞击属于非线性动力学[19]问题，甲板涂层由于其特殊性[20]，仅靠计算分析不能保证力学特性参数的准确性。因此借助试验测试手段对拦阻钩与甲板撞击反弹的力学特性进行研究，修正仿真模型中的恢复系数等参数，以便得到准确可靠的仿真模型，进而对拦阻钩的碰撞反弹性进行深入的研究。

2.1 试验方法

拦阻钩与甲板撞击反弹的试验方案如图3所示。拦阻钩安装在吊篮侧面，通过提升机构将吊篮装置提升至指定高度投放，以模拟设定的撞击时的下沉速度；钩头正下方是旋转盘系统，通过钩头在旋转盘上垂向投影位置与旋转盘中心轴线的相对线速度来模拟航向速度；下方的旋转盘可以调整一侧高度，用于抬高或降低以模拟撞击时不同的甲板角。为了更准确地模拟碰撞工况，在转盘上涂上甲板涂层，以便碰撞点的材料属性、力学性能均与甲板上的相同，便于研究不同参数对于拦阻钩撞击甲板反弹的力学特性影响。

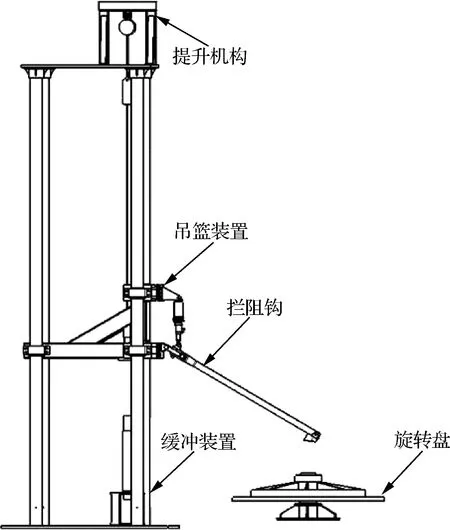
图3 台架结构装配图

试验系统模拟的下沉速度与吊篮提升高度间关系为

(14)

式中:Md为吊篮装置和拦阻钩系统的总质量;g为重力加速度;h为投放高度;f(t)为投放过程中吊篮受到的摩擦力。

试验系统模拟的航向速度与旋转盘系统转速间关系为

vr=2πNrr

(15)

式中:Nr为旋转盘转速;r为钩头与旋转盘接触的旋转半径。

2.2 模型校验

利用拦阻钩撞击甲板试验结果与仿真结果进行对比，修正仿真模型中一些难以直接测量的关键力学参数，比如甲板(含涂层)时的恢复系数，从而得到更为准确的动力学模型。本文研究的拦阻钩参数如下：拦阻钩关于质心转动惯量JC=65 kg·m2，拦阻钩质量m=89 kg，拦阻钩总长l=2.2 m，质心距上铰接点距离l1=0.96 m，缓冲器初始压强P0=2 MPa，恢复系数e=0.43。

对模型进行参数修正后，将仿真与试验结果进行对比，工况对比如表1所示。结果如表2所示。

表1 仿真与试验的工况对比

表2 仿真与试验结果对比

由对比结果可知，误差均在5%以内，证明建立的动力学模型比较准确，可用于拦阻钩碰撞反弹动力学仿真分析。

3 缓冲器安装形式对弹跳影响

主要仿真参数初始取值如下：JC=65 kg·m2,m=89 kg,l=2.2 m,l1=0.96 m,P0=2 MPa,e=0.43,vt=3.6 m/s,vr=55 m/s,β=31°。

由于缓冲器的安装形式在一定程度上影响拦阻钩的碰撞反弹特性，为研究不同安装形式的缓冲器对碰撞反弹的影响，本文选取3种安装形式进行对比研究。前文已经对其中一种安装形式的缓冲器进行了描述和分析，称其为Ⅰ型缓冲器。如图4所示缓冲器安装形式的拦阻钩，称其为Ⅱ型缓冲器。Ⅱ型缓冲器与Ⅰ型缓冲器结构形式相近，仅机身的安装点不同。

由图4中几何关系可得

图4 Ⅱ型拦阻钩缓冲器

(16)

由动量矩定理可得

(17)

第3种拦阻钩缓冲器形式如图5所示，称为Ⅲ型缓冲器。图中:φ为拦阻钩与垂直甲板方向夹角;γ为拦阻钩缓冲器与拦阻钩轴向延长线的夹角。Ⅲ型缓冲器区别于Ⅰ型、Ⅱ型缓冲器主要在其作用力臂BP分别与机身、缓冲器轴向连接。上述3种缓冲器形式的最大区别在于缓冲器与拦阻钩以及机身连接点布局完全不同。

图5 Ⅲ型拦阻钩缓冲器形式

由图5中几何关系可得

(18)

式中:δ为缓冲器与其作用力臂之间夹角。

由动量矩定理可得

(19)

分别对上述3种缓冲器取相同的着舰工况进行仿真计算，缓冲器形式对弹跳高度和缓冲器作用力的影响如图6和图7所示。可以看出，Ⅲ型缓冲器的弹跳高度在三者中最低，但缓冲器作用力峰值最大，其主要原因是由于Ⅲ型缓冲器的安装形式使得缓冲器对拦阻钩的抑制效果更为明显；Ⅱ型的弹跳高度与Ⅲ型相近，缓冲器作用力峰值在三者中最低；Ⅰ型弹跳高度最大，缓冲器作用力介于三者之间。

图6 缓冲器形式对弹跳高度的影响

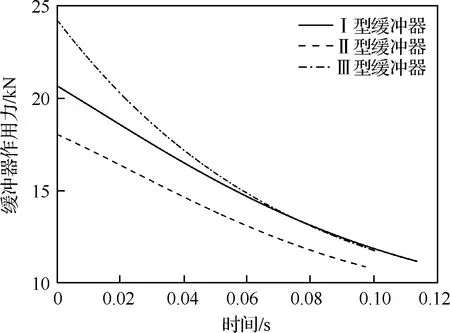
图7 缓冲器形式对缓冲器作用力的影响

综上所述，在相同参数设置下，Ⅱ型安装形式的缓冲器弹跳高度介于Ⅰ型和Ⅲ型之间，为54.3 mm，缓冲器作用力峰值最低，为16.1 kN。综合考虑弹跳高度、弹跳位移和缓冲器作用力时认为Ⅱ型缓冲器为最优解。

4 重心位置对Ⅱ型拦阻钩撞击反弹影响

根据前文分析，选取Ⅱ型安装形式的拦阻钩为研究对象，分析不同的重心位置下的弹跳响应情况。取重心位置距上铰接点距离分别为0.8 m、0.96 m、1.2 m，此时初始压强为2 MPa，油孔半径为4 mm。

重心位置对弹跳高度和缓冲器作用力的影响见图8和图9。可以看出，随着重心距上铰接点长度的增大，拦阻钩与甲板撞击后的初次反弹高度变大，弹跳距离也明显变大，且过程中缓冲器作用力随该距离的增大而减小。重心距上铰接点长度l1对弹跳高度和缓冲器作用力的影响均较大，在拦阻钩总长一定的条件下，重心位置距上铰接点长度较短时撞击反弹性能较好。

图8 重心位置对弹跳高度的影响

图9 重心位置对缓冲器作用力的影响

5 结构参数对反弹高度的影响分析

5.1 油孔半径对拦阻钩撞击反弹影响

为了分析纵向缓冲器油孔半径对拦阻钩弹跳反弹性能的影响，选取不同的纵向缓冲器油孔半径进行分析，分别为3 mm、4 mm、5 mm，此时初始压强为2 MPa。

由图10和图11可以看出，油孔半径对两者的影响幅度都较大。随着油孔半径的增大，拦阻钩与甲板撞击后的初次反弹高度变大，缓冲器作用力急剧变小，当油孔半径为5 mm时，弹跳高度达到了55.4 mm，缓冲器作用力为12.9 kN。其原因是油孔半径变大，阻尼力相应变小，对于拦阻钩垂向弹跳的限制减小，从而使得反弹高度急剧变大。

图10 油孔半径对弹跳高度的影响

图11 油孔半径对缓冲器作用力的影响

5.2 初始压强对拦阻钩撞击反弹影响

取油孔半径4 mm，分析纵向缓冲器初始压强分别为0.5 MPa、1 MPa、2 MPa、4 MPa时撞击反弹性能的变化趋势。

初始压强对弹跳高度和缓冲器作用力的影响如图12和图13所示。可以看出，随着初始压强的增大，拦阻钩与甲板撞击后的初次反弹高度变小，且弹跳距离也明显减小，在初始压强为0.5 MPa时第1次弹跳距离超过规定的6.1 m，极有可能造成挂索失败。其原因是随着初始压强的增大，缓冲器作用力急剧增大。

图12 初始压强对弹跳高度的影响

图13 初始压强对缓冲器作用力的影响

影响参数及影响幅度对比如表3所示。

表3 结构参数影响

5.3 基于双结构参数影响的设计优化

根据前文所述可以得出拦阻钩纵向缓冲器油孔半径、初始压强以及重心位置等单参数对弹跳距离、弹跳高度和缓冲器作用力的影响，结合表3可以看出，油孔半径和初始压强对弹跳高度和缓冲器作用力的影响趋势相反。针对此现象进行基于双结构参数影响的寻优设计，目的是为了减小拦阻钩的反弹高度和缓冲器作用力，使之在给定边界条件下得出最佳参数组合。

取油孔半径为3～5 mm，以0.1 mm为步长，取初始压强为0.5～4 MPa，以0.1 MPa为步长，共计756个工况。对756个工况下弹跳距离、弹跳高度和缓冲器作用力进行仿真计算，结果如图14～图19所示。

图14 弹跳位移分布三维视图

图15 弹跳位移分布二维视图

图16 弹跳高度分布三维视图

图17 弹跳高度分布二维视图

图18 缓冲器作用力分布三维视图

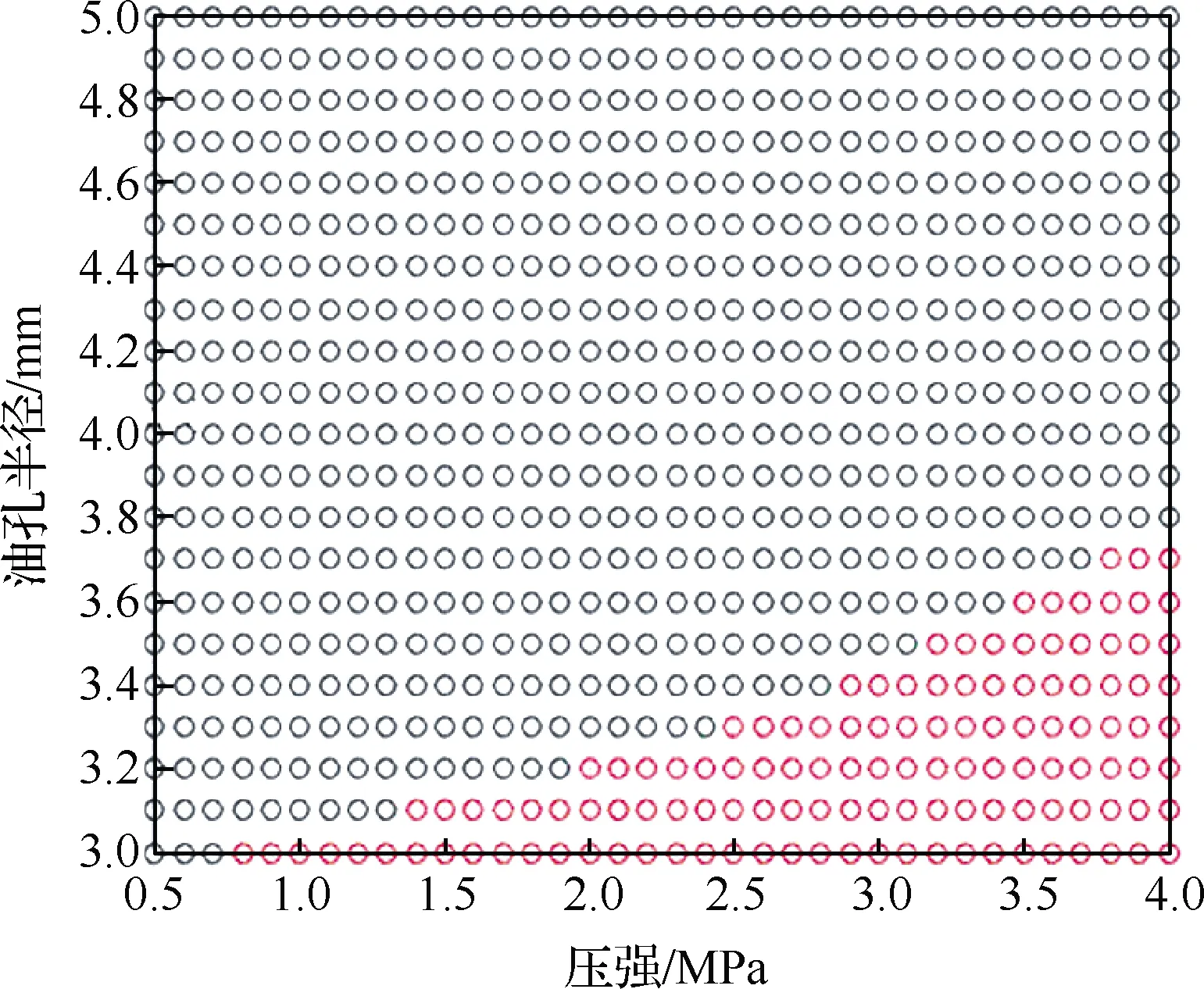
图19 缓冲器作用力分布二维视图

设置弹跳位移大于6.1 m、弹跳高度大于100 mm、缓冲器作用力大于30 kN为红色点，表示该结果参数超出限制范围的工况，即为不满足弹跳限制条件，判定为挂索失败。

图14、图16和图18中三维视图为油孔半径、压强对于弹跳位移、弹跳高度以及缓冲器作用力的关系。从图中可以明显看出，各结果参数与自变量并不是线性关系，弹跳位移与弹跳高度的空间分布较类似，呈马鞍形，缓冲器作用力的空间分布呈管状，且缓冲器作用力分布中的点型趋势也与另外两者不一致。

图15、图17和图19中二维视图分别为弹跳位移、弹跳高度和缓冲器作用力分布下的初始压强-油孔半径视图。在二维视图中，可以明显地看出弹跳位移与弹跳高度的红点分布在油孔半径大、初始压强小处，相比较下弹跳位移的红点分布更广，缓冲器作用力的红点分布在油孔半径小、初始压强大处。

由此可以得出在油孔半径大、初始压强小时，对应的缓冲器作用力必然小，缓冲器作用力小必然引起弹跳位移和弹跳高度增加，也就是所谓的缓冲作用有限、压不住弹跳。

在满足缓冲器作用力不超过30 kN条件下，以弹跳位移和弹跳高度最小作为优化目标，对油孔半径(3～5 mm范围内)和初始压强(0.5～4 MPa范围内)进行寻优。以ISIGHT和MATLAB联合仿真方式，采用多岛遗传算法(MIGA)对油孔半径和初始压强进行寻优设计，搭建的模型如图20所示。其中，MATLAB调用的Simulink模型设置步长为定步长0.000 1 s，求解器采用ode3(Bogacki-Shampine)算法，该步长经检验满足收敛要求。

图20 ISIGHT调用MATLAB的优化模型

优化的整体框架包括ISIGHT优化模块以及Simulink计算模块。首先根据初始值优化操作，此后每一次迭代都是有ISIGHT通过遗传操作生成新的参数值传递至Simulink进行迭代计算，求解得到的油孔半径和初始压强再回传至ISIGHT，检测前后2次迭代是否收敛，并进入下一次迭代，如此循环直至满足收敛要求。

最终寻优得到结果如表4所示。由仿真结果可知，当纵向缓冲器油孔半径为3.7 mm，初始压强为3.7 MPa时，拦阻钩弹跳位移为3.2 m，弹跳高度为33.4 mm，缓冲器作用力为29.6 kN，拦阻钩反弹现象得到了较好的抑制，缓冲器作用力也在限制范围之内，本文认为这是一个较为理想的参数组合。

表4 结构参数寻优结果

6 结 论

针对舰载机着舰时拦阻钩与甲板撞击反弹的问题，建立了拦阻钩碰撞反弹动力学模型，通过试验结果对模型进行了修正，研究了缓冲器安装形式、拦阻钩重心位置和缓冲器结构参数对碰撞反弹性能的影响，并且提出了一种基于缓冲器双结构参数影响的设计优化方法，通过综合分析得到了以下结论:

1)选取3种缓冲器安装形式进行对比研究，在相同参数设置下，Ⅱ型安装形式的缓冲器弹跳高度约为54.3 mm，介于Ⅰ型和Ⅲ型之间，缓冲器作用力峰值最低为16.1 kN，本文认为Ⅱ型缓冲器安装形式最好。

2)拦阻钩重心位置对拦阻钩碰撞反弹高度影响较大，对缓冲器作用力影响极小。重心距上铰接点长度从0.8 m增大至1.2 m时，初次弹跳高度从34.9 mm增大至54.7 mm，增长了56.6%。因此在拦阻钩总长一定的条件下，重心位置距上铰接点长度较短时撞击反弹性能良好，在设计拦阻钩时应使拦阻钩重心位置尽可能接近铰接点。

3)纵向缓冲器的油孔半径对拦阻钩弹跳高度影响较大，随着油孔半径的增大，初次弹跳高度和弹跳距离明显增大，缓冲器作用力急剧减小；初始压强与初次反弹高度和弹跳距离呈负相关，和缓冲器作用力呈正相关。综合考虑油孔半径和初始压强进行优化设计，得出了一组最佳参数组合，即油孔半径和初始压强分别为3.7 mm和3.7 MPa时拦阻钩的反弹可以很好地被抑制，有利于提高拦阻着舰的安全性。

4)本文分析了拦阻钩缓冲器安装形式、重心位置以及结构参数等对碰撞反弹性能的影响，通过双参数结构优化设计给出了一组最佳参数组合，研究结果在很大程度上反映了拦阻钩的碰撞反弹性能，对新型拦阻钩设计具有一定的指导作用。