基于集成式长短期记忆神经网络模型的股价涨跌预测分析

赵丽君，王峻楠，程建华

(安徽大学 经济学院，安徽 合肥 230601)

1952年，Markowitz提出了均值-方差模型，为使用线性模型预测股票收益奠定了理论基础，推动了CAPM(capital asset pricing model)的发展.1976年,Ross提出套利定价模型，该理论认为：受GDP增长、通货膨胀等因素影响，股票市场中会出现短暂的套利机会，所以股票的期望收益率还受宏观因素的影响.Fama和French注意到公司账面信息能够有效挤压公司股价中的泡沫，共同提出了3因子模型(Fama-French-3-factor-model)(即投资市场收益率、宏观形势和公司账面3因子)，通过3个因子的线性组合刻画股价收益率.然而，上述线性分析方法只能对变量间的既定关系做出相合估计.金融市场在突发事件影响下，金融变量间的既定关系会不断变化，使用线性模型的假设会让个股收益率序列数据呈现出具有低信噪比和厚尾分布等特点，因此预测的准确性较低.

对个股收益率的分析，准确预测的方法极具价值.机器学习算法因其出色的预测能力，已是量化投资分析的新宠.其中，神经网络模型在多种市场的价格预测方面得到广泛应用.LSTM(long short-term memory)神经网络模型由Hochreiter和Schmidhuber提出,LSTM能够学习时间序列数据中存在的记忆性，在语言识别、人机交互等人工智能领域，LSTM的预测能力也远胜于BP(back propagation)神经网络等模型.该模型缓解了循环神经网络模型(recurrent neural network，简称RNN)学习长期序列时的梯度消失、梯度爆炸问题，对时间序列数据的学习能力更强.已有学者尝试将LSTM应用于股票市场进行股市收益预测，但他们建立的LSTM主要应对单一来源数据，模型的预测准确率有限.尽管如此，Siami等发现在经济、金融时间序列数据上，LSTM在预测准确率方面明显优于基于Box-Jenkins预测逻辑的ARIMA(auto regressive integrated moving average)模型，这种优势还不会受到过度拟合问题的显著影响.裴大卫等将多因子预测股价的思想和LSTM模型相结合，发现多因子有助于提高LSTM模型的稳健性.陈卫华等使用LSTM发现网络上相关的发帖量也是影响沪深300指数的因子之一.学界已经开始尝试改良深度学习基础模型.

论文借鉴Fama和French的3因子模型所表达的思想，以构建ensemble LSTM这一可以学习多源数据的框架，将货币因素、股市交易历史信息以及企业财务情况等多源数据纳入模型的学习范围.经过对沪深300域中16支股票分析，发现ensemble LSTM比LSTM的预测能力更强，即通过ensemble LSTM处理多源数据，能产生更为准确的股价涨跌预测.

1 预测建模的理论基础

1.1 LSTM神经网络结构

Hochreiter和Schmidhuber于1997年提出了长短期记忆神经网络模型(LSTM)，该模型可以解决循环神经网络RNN在学习较长时间序列时发生的“梯度问题”.RNN和传统前馈神经网络的不同之处在于，不同时刻的“隐层”间由数据传输结构(memorycell)连接，让前一时刻“隐层”中的记忆影响后面的时刻.然而，RNN的memorycell不具备选择性丢弃与保存信息的功能，因此造成过度学习的问题.LSTM在RNN的基础上，对memorycell的循环机制增加了3个门控单元，用于精炼对长期时间序列的学习过程.LSTM的memorycell结构如图1所示.

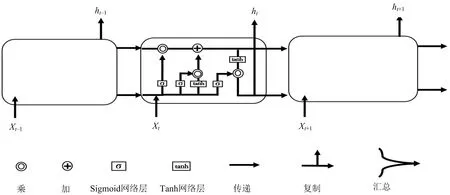
图1 LSTM神经网络memorycell结构图

图1所示结构为LSTM神经网络隐层之间的链状传输结构，通常也称之为LSTM层.在

t

时刻，memorycell同时接受3种信息的输入，分别是

t

-1时刻memorycell的状态

C

-1、

t

-1时刻memorycell的实际输出

h

-1以及

t

时刻memorycell输入的向量

X

.通过每一个memorycell内部都存在的3个门状结构(遗忘门、输入门、输出门)对信息进行存储和过滤.这些门状结构在处理信息时拥有不同的功能.遗忘门：决定对

t

-1时刻memorycell的状态

C

-1保留多少.计算过程如下

f

=

σ

(,

X

+,

h

-1+

b

)

.

(1)

输入门：决定

t

时刻memorycell输入的向量

X

保留多少到

t

时刻的memorycell的状态.计算过程如下

(2)

(3)

输出门：决定

t

时刻memorycell的状态

C

保留多少到

t

时刻memorycell的实际输出

h

.计算过程如下

O

=

σ

(,

X

+,

h

-1+

b

)，

(4)

(5)

h

=

O

*tanh(

C

),

(6)

σ

(

x

)=(1+e-)-1，

(7)

tan

h

(

x

)=(e-e-)

/

(e+e-)

.

(8)

1.2 ensemble LSTM神经网络结构

尽管在股市中因子的既定分布会因为外在因素改变，但不能排除可变分布受到因子间潜在确定关系的长期影响.选择性抛弃之前的记忆为LSTM较RNN的优势，在股市预测中或成为劣势，可能会抛弃了因子间潜在关系的长期影响.论文考察的因子间潜在关系是因子间的均衡关系，将影响个股收益率的因子分为3个来源：(A)宏观政策直接影响的定期储蓄利率和人民币兑换主要外币的汇率；(B)公司定期发布的财务数据(量化因子)；(C)个股的交易信息.由于MM(modigliani miller theorem)定理(企业资本构成不影响企业市场价值)在现实中不成立，公司财务会受到金融环境的影响，所以(A)和(C)将决定(B)；又因为宏观政策和公司的财务将影响个股收益，所以(A)和(B)也将决定(C).这就构成了一个确定的均衡关系.LSTM会将此3个来源的数据合并为一列向量(和单来源一样)，在每一时刻随机选取权重矩阵抛弃前一时刻的信息，所以几乎不可能利用上述确定的均衡关系进行预测.即便前一时刻的信息包含长期均衡关系，在后一时刻也会被随机权重丢弃.

针对LSTM在个股收益率预测中处理多源数据的弊端，论文构建多个LSTM网络的并联结构——ensemble LSTM.图2展示了ensemble LSTM神经网络的结构.首先，根据训练集，确定3个不同来源的数据在LSTM层中的节点数，某来源分配到的节点数越多，代表该来源数据在预测中越重要；各来源的节点数在预测时保持不变，代表确定的均衡关系始终影响着个股收益率.论文称这一层运算为“动态网络生成”.其后，给定输入层的节点数，各LSTM网络彼此独立学习单来源的时间序列数据，获得各来源的解释变量与被解释变量间的时间依赖关系.LSTM仅抛弃单来源前一时刻遗留的记忆，而不是由“动态网络生成”机制形成的均衡关系，在学习过程中，各来源数据间也不存在节点连接去改变均衡关系.最终，在稠密层对各LSTM网络的输出进行集成，在输出层以softmax函数输出二维向量，用于预测股票的涨或跌.

所以，ensemble LSTM具有两个潜在优势：

(1)ensemble LSTM基于长期确定的多源数据间的均衡关系进行股价涨跌预测，其预测的准确率可能比LSTM更高；

(2)ensemble LSTM基于动态网络生成机制为内嵌的LSTM设置节点数，且内嵌的LSTM在单来源数据上独立学习，避免了不同来源数据间的节点关联，所以可能比LSTM预测使用的运算资源更少.

通常认为神经网络模型的节点数越多，模型的自由度就越高，该模型对样本数据进行拟合时的误差也就越小.然而，节点数不能无限增加，在构造神经网络的结构时必须在节点数上进行权衡.论文在ensemble LSTM中构建“动态网络生成”机制，这一机制使得ensemble LSTM神经网络模型在对每支股票的未来涨跌情况进行预测之前，会根据各个数据源的历史数据(即训练集)逐一计算各个数据源对该只股票涨跌的影响程度，即特征重要度.在指定ensemble LSTM节点总数的条件下，“动态网络生成”机制根据各数据源的特征重要度生成相应节点数，对于没有特征重要性的变量选择用随机赋权和其他因子平均重要度最小值代替特征重要度，并在训练时不断更新调整节点数.当ensemble LSTM对训练集时间序列数据学习完毕后，各来源数据的隐层节点数就分配完成，在进行检验和预测时不会改变.传统的集成算法也具备类似的动态建模机制，如AdaBoost(adaptive boosting).

图2 ensemble LSTM神经网络模型结构

2 多源数据选取及说明

为综合考量各来源数据对股价造成的影响，进而准确地预测个股收益，论文分别从货币市场、公司财务报表以及证券市场交易信息选取研究数据，数据获取自通联量化平台(https://uqer.datayes.com/)，数据时间段为2015年6月至2019年12月.其中直接受到货币政策影响的变量包括汇率变动、利率调整,而代表投资者情绪的RSI(relative strength index)指标等，与公司财务数据共同放在了量化因子之中.

2.1 货币政策数据

对于A股而言，实体经济变量和个股收益率间大多具有正相关性.作为宏观经济“指挥棒”的利率却与股票价格存在显著的负相关性.在无风险、利率较高的时候，投资者更倾向于选择债券、储蓄等投资方式以期获得低风险收益，而需求发生转变时，可能造成股价下跌.人民币汇率对资金流动有显著的冲击，即便存在资本管制，人民币走弱也会诱发投资者加速兑换外币，或者购买黄金等保值金属，进而带来股价的变化.

论文选择以利率变化率、汇率变化率作为反映货币政策变动的代表性指标，其中利率变化率选择人民币兑美元实际汇率变化率、人民币兑日元实际汇率变化率、人民币兑欧元实际汇率变化率、人民币兑澳元实际汇率变化率，利率变化率选择一年期国债收益率变化率.表1为货币政策变动代表性指标.

表1 货币政策变动代表性指标

2.2 量化因子数据

量化因子是股票价格外在影响因素的数学表达，这些因素来源于金融经济规律以及市场经验.市场上有数以百计的因子，它们在不同的市场环境下，或多或少会起作用，从量化分析的角度来看，这些因子和收益率间有潜在的因果关系.目前，国内通联量化平台提供10大类共计424个量化因子，论文从该因子库获取量化因子数据.经查阅券商研报及相关文献，并经过多轮因子回测检验，选取的量化因子如表2所示.

表2 量化因子表

在金融经济学中，量化因子用于预测超额收益率(个股收益率-无风险回报率)，而量化因子的特征重要度就是该因子在预测中的重要性.表2中，13个量化因子的特征重要度均大于3.5%，不存在冗余特征.关于特征重要度的计算方法参考Breiman建立的随机森林模型，Breiman提出了以基尼不纯系数(gini impurity)为基础的特征重要度评估方法，此后，基于随机森林模型计算各所选特征对目标变量的重要度已成为一种通用方法.

如前所述，Ross在套利定价模型给出个股超额收益率也会受到诸如货币政策等宏观因素的影响，然而宏观因素主要决定的是无风险资产的回报率(定期储蓄的利率减去平均汇率变化).谨慎起见，论文不为货币政策因子设定特征重要性，仅为反映公司基本面的量化因子和个股历史行情设定特征重要性.因子的特征重要性是论文构建动态网络生成机制的重要依据，部分决定了训练过程，而各来源在预测中的节点数最终是在完成训练后确定.根据特征重要性设置训练，为LSTM和ensemble LSTM的学习过程节约了运算资源.

2.3 股票历史行情数据

在传统金融时间序列分析中，个股历史交易数据是作预测时最重要的数据来源.论文从股票行情数据中选取了9个常用的特征作为指标,如表3所示.

表3 股票历史行情数据候选特征表

3 实验与分析

论文从沪深300指数成份股中，随机选取16家上市公司的股票作为研究样本，这些上市公司来自不同的行业，主营业务差异较大.

由于A股市场在2015年4月呈现快速上涨的趋势，而在当年6月又发生大幅下跌，此时间段内股市的异常波动不能反映长期趋势，会被LSTM和ensemble LSTM模型在学习中遗忘.为节约运算资源，论文以2015年6月为起点，选取了2015年6月至2019年12月期间样本股票的相关数据，并按表4所示划分训练集、检验集和测试集.

表4 实验数据划分表

数据标签(label).考察股票在下一个交易日的收益率大于零(涨)或者小于等于零(跌)，则该日观测数据标签为1或者 0.训练之前，所有数据均经过标准化处理.

对模型进行评估时，选取了准确率(Accuracy)作为该分类模型的评估指标.令TP为股价在次日上涨(label=1)且模型也预测次日上涨(预测label=1)的天数，TN为股价次日下跌(label=0)且模型也预测次日下跌(预测label=0)的天数，FP为label=0但模型预测label=1的天数，FN为label=1但模型预测label=0的天数.

将模型预测的准确率定义如下

(9)

选择交叉熵函数作为损失函数

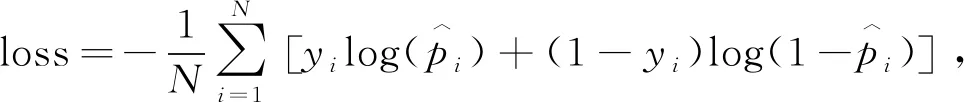
(10)

3.1 训练和检验

ensemble LSTM包含3个子神经网络结构，各网络内部均含有多个大小一致的LSTM层.在LSTM神经网络中，节点数不能无限增大，否则不仅浪费运算资源，也会发生过度拟合问题.如前所述，使用动态网络生成机制，在有限的加总节点数下，分配各子神经网络的节点数.

图3，4给出在不同隐层节点数下，基于个股华侨城A的数据，LSTM和ensemble LSTM在训练集和检验集中的准确率.将隐层节点数设为64，128和256，为考察各节点下准确率的收敛情况，学习次数统一设为200次.使用LSTM，大约在学习75次之后，准确率接近收敛，其中64和128节点的准确率收敛到0.81左右，而256节点的准确率收敛到0.87左右.使用ensemble LSTM，通过200次深度学习，256节点的准确率可以提高到0.91左右，64和128节点的准确率也较LSTM有所提升，最终可以达到0.83左右.而且ensemble LSTM在256节点下，其准确率在200次学习后仍有提升可能，说明ensemble LSTM在预测准确性上具有优势.

仍基于个股华侨城A的数据，图4给出在不同隐层节点数下，LSTM和ensemble LSTM在检验集中的准确率.大约通过130次学习，LSTM的准确率达到收敛，其中128和64节点的准确率收敛到0.81左右，且256节点的准确率也收敛到0.82左右.同样经过大约130次学习，ensemble LSTM的准确率也发生收敛，其中256和128节点的准确率收敛到0.83左右，而64节点的准确率也收敛到0.82左右.在检验过程中，ensemble LSTM模型仅采用128隐层节点数就能实现比采用256节点数的LSTM更高的预测准确率，所以ensemble LSTM能够实现运算资源的节约.

图3 不同隐层节点数下模型在训练集中的准确率

图4 不同隐层节点数下模型在检验集中的准确率

通常，规模适中的神经网络结构既可以满足较高的预测准确率，也兼具较高的鲁棒性，所以论文不考虑比256更高的节点数.为了保障测试的公平，弥补128和64节点下LSTM在准确率上的先天性不足，故对所有16支个股使用256节点数，建立LSTM和ensemble LSTM的预测模型.

3.2 测试和预测准确率分析

为了节约运算资源，论文未进行超参数空间的全局搜索，仅仅通过网格搜索算法，搜索当前超参数空间下的最优超参数.论文在进行LSTM与ensemble LSTM神经网络模型的比较分析时，包括节点数、丢弃概率、学习率、批大小等超参数均保持一致.这里仍以华侨城A相关数据为例，比较了LSTM和ensemble LSTM在测试集中的预测性能，如表5所示.

表5 测试集中LSTM与ensemble LSTM模型预测对比

由表5可知，

ensemble

LSTM

不仅准确率(均值)比

LSTM

更高，而且所需参数也比

LSTM

更少(前者估计的参数总数仅为后者的44

%

)，再一次说明

ensemble

LSTM

可以在不损失预测准确率的前提下节约运算资源

.

需要说明的是：深度学习模型的预测，其单次预测的准确率是没有意义的

.LSTM

和

ensemble

LSTM

在做预测时，都受到随机权重的影响，每一次预测的结果和准确率会有差异，所以模型预测的准确率应当被定义“模型稳定地输出准确的预测序列”

.

论文使用

LSTM

和

ensemble

LSTM

分别对16家上市公司股票进行了35次独立预测

.

图5给出在测试集上两个模型预测16支个股涨跌的准确率的核密度分布

.

图5 两种预测模型在16支个股上预测准确率的核密度分布图

对16支个股做如下分类：①35次预测后，

ensemble

LSTM

预测准确率均值高于

LSTM

，且预测准确率的峰度大于

LSTM

；②35次预测后，

ensemble

LSTM

预测准确率均值远高于

LSTM

，但预测准确率的峰度不大于

LSTM

；③其他

.

对第①类个股，使用

ensemble

LSTM

，可以稳定地产生更为精确的股价涨跌预测

.

这类股票有7支,分别是：平安银行、徐工机械、长安汽车、中公教育、包钢股份、中国石化、上海建工

.

对第②类个股，使用

ensemble

LSTM

，其预测准确率明显高于使用

LSTM

，虽然预测的高准确率并不是稳定产生的，但准确率低于

LSTM

的可能性较小

.

这类股票有7支，分别是华侨城

A

、中联重科、泸州老窖、浦发银行、三一重工、上汽集团和陆家嘴，在这7支个股上，

ensemble

LSTM

和

LSTM

的平均准确率分别为80

.

90

%

，77

.

97

%.

第③类个股，仅有2支，分别是中兴通讯、芒果超媒

.

对这两只个股，

ensemble

LSTM

的准确率虽然低于

LSTM

，但差距较小，平均准确率之差分别为-0

.

7

%

,-0

.

32

%.

其中，

ensemble

LSTM

对三一重工的预测准确率明显右偏，所以对于此个股，

ensemble

LSTM

仍具有提高预测准确率的可能性

.

LSTM

和

ensemble

LSTM

在16支股票的测试集中预测性能对比如表6所示

.

表6 LSTM和ensemble LSTM稳定预测的性能对比

综合来看，在对16支个股共1 120次测试中，ensemble LSTM表现出的预测准确率比LSTM更好，也更加稳定.ensemble LSTM的平均预测准确率、平均召回率(被正确预测的上涨天数占总上涨天数的比率)、平均精确率(被预测为上涨的天数中实际也上涨的天数的比率)分别为80.83%，74.02%，84.36%，而LSTM神经网络模型平均预测准确率、平均召回率、平均精确率分别为78.18%，70.30%，82.18%.因此，无论是对于日常交易还是对长期做多或做空的操作，ensemble LSTM都比LSTM更具有价值.

需要说明的是：同一种神经网络模型对不同的股票进行预测时，预测表现会有较大的差异，这可能是因为选取的各股所处行业不同，股票对因子的敏感性也存在较大差异.在实际应用中，ensemble LSTM可以针对个股调整影响因子，进一步提高模型的预测准确率.

4 结束语

使用LSTM学习多源时间序列数据时，必须将多个来源的时间序列数据整合为一个时间序列数据.对于股价预测而言，LSTM将遗忘不同来源数据间的长期均衡关系，所以论文对其预测准确率存疑.论文构建了具有动态网络生成机制的ensemble LSTM神经网络模型，通过训练集确定各来源数据在深度学习中的隐层节点数，代表各来源数据间的长期关系，并在预测时让LSTM在给定的节点数上独立学习各来源数据，所以ensemble LSTM既具有提高股价预测准确率的可能，也具有节约运算资源的潜力.