“问本数学”理念浅析
万正茜

“问本数学”是在数学课堂上以问——教师设问、追问和学生叩问、追问、反问等为主要教学手段,以探求数学本质为学习目的的教学理念。笔者以小学数学二年级下册除法单元“平均分的认识”为例,谈谈“问本数学”的实施路径。
一、叩问概念本质,展现真实操作
低年级学生抽象概括能力不强,理解抽象概念需要借助直观事物。这就要求教师在讲授抽象概念时,先创设问题情境,引导学生进行直观操作。
执教《分物游戏》时,笔者创设情境:孙悟空在天宫待久了,决定回花果山看望他的徒子徒孙。他从王母娘娘的蟠桃园中摘了4个仙桃,送给前来迎接它的小猴乐乐和欢欢。这4个仙桃可以怎样分呢?学生动手操作自主分桃,出现了五种不同的分法:(4,0)(3,1)(2,2)(1,3)(0,4)。笔者让学生思考欢欢与乐乐会同意哪一种分法,并说明理由。通过讨论,学生推断它们会选择每只小猴分2个仙桃,因为每人分得同样多,才显得公平。那么,什么是“平均分”呢?笔者引导学生对比五种分法,并将其分成两类。学生发现(4,0)(3,1)(1,3)(0,4)这四种分法每份不相等,属于“不等分”;(2,2)这种分法,每份同样多,属于“平均分”。因此,平均分是指每份数量同样多。学生借助直观操作,在教师的叩问下探究“平均分”的数学本质,此时学生只是从分物的结果上进行判断,是一种直观感受,对概念的认识是浅层次的感知。
二、追问分物方法,发现概念要素
理解数学概念时,抓住概念要素是关键。平均分的四大要素是分物总量、平均分、份数、每份数。教学中,教师追问分物方法,引导学生发现概念要素。
分桃子游戲中,学生对平均分的理解停留在实物表征的层面。为加深学生对平均分的理解,笔者引导学生通过图画表征进入第二个分物游戏——12根萝卜,平均分给3只小兔,每只小兔分得几根萝卜?结合分萝卜的具体情境,笔者追问:①分什么?(12根萝卜,分物总数一目了然。)②怎么分?你是如何知道的?(平均分,即每只小兔分得同样多。)③分几份?(分给3只小兔,也就是把萝卜分成3份。)④每只小兔分得几根萝卜?就是每份是几?(学生画图后得出每份4根。)这个游戏中,平均分的四大要素逐一亮相,为后面除法概念的产生打下了基础。
笔者继续追问:只能4个4个地分吗?还可以怎么分?学生陆续给出其他三种平均分的方法。从4个4个地分(1次完成),到1个1个地分(分4次),到2个2个地分(分2次),到3个3个地分(先每只兔子分3根,再每只兔子分1根),平均分的方法变得多样化,学生的思维被彻底激活,课堂的学习气氛热烈。
学生把不同分法分享完毕之后,笔者抛出第二个问题:“对比不同的分法,你发现了什么?”通过对比分析,学生明白:当分物总数一定时,每次分的根数不同,分的次数也不一样。每次分的根数少一些,则分的次数多。如果每次分的根数多一些,则分的次数少。每次分的根数与次数之间是相反的关系。只要每次分的根数一样,那么最终分的每份数结果相同,都是平均分。
三、反问记录方法,深化概念认知
在教师的反问下,学生不断简化记录方法,深化对概念的认知。
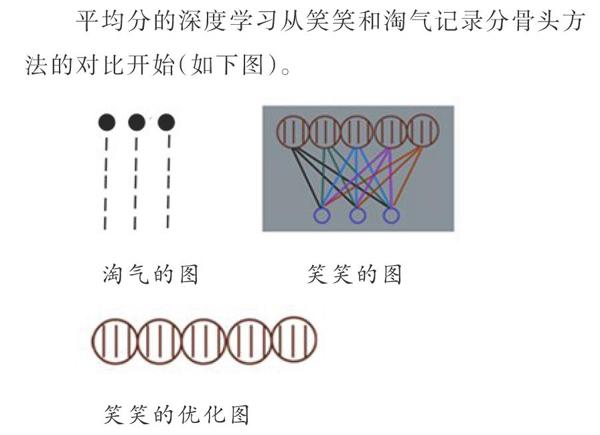
平均分的深度学习从笑笑和淘气记录分骨头方法的对比开始(如下图)。
笔者提问:“谁看懂了笑笑的分法?”学生发现:笑笑的分法和淘气的分法是完全一样的,都是1个1个地分,可是笑笑原来记录的方式太复杂。笔者反问:如何简化笑笑的记录呢?学生给出笑笑的优化图。有3只小狗,所以一次拿3根骨头出来分,每只小狗每次分1根。分一次就圈3根,圈了5次等于分了5次,每只小狗就分了5根。笔者肯定了学生的思路,并指出:这个记录图优化的过程告诉大家,“把15根骨头平均分成3份,每份几根”这个问题和“15里面有几个3”的结果一样,所以有3只小狗,我们就每3根骨头圈一次,圈了5次,15里面有5个3,所以每只小狗分5根骨头。前面的问题是把15等分3份,后面的问题是15包含几个3。通过比较淘气与笑笑的记录方式,学生再一次经历平均分图示方法由繁而简的过程,在分物的过程中深化了对“平均分”的理解。
四、探究除法算式,训练抽象思维
二年级上册除法单元前四课时内容的教学目标分别是:判断什么是平均分,积累平均分物的经验;知道平均分的两种情况;体验把大数目平均分过程的多样性,用表格代替画圈获取试商经验;结合分物情境,抽象理解除法算式。平均分概念的建立旨在为除法计算做铺垫,教学中,教师应引导学生在平均分的基础上探究除法算式,训练学生的抽象思维。
学生关于平均分的学习,经历了实物表征、图画表征的过程,到《分香蕉》一课正式进入符号表征阶段。仍以“12根萝卜平均分给3只小兔,每只小兔分得几根萝卜?”这一问题情境为例。
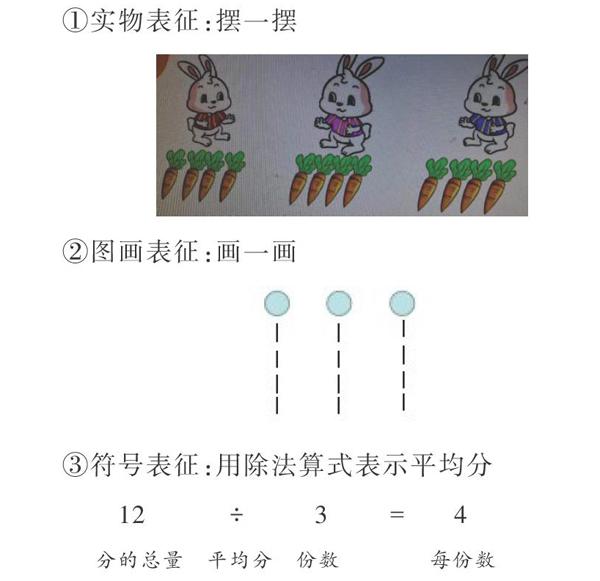
①实物表征:摆一摆
②图画表征:画一画
③符号表征:用除法算式表示平均分
从平均分的三种表征方式来看,实际就是概念从表象到形式化的过程。从每份4个萝卜同样多的表象,过渡到4根小棒代替4个萝卜,最后用商4表示每份数。记录平均分的过程与结果,在抽象的过程中逐步简化,展现了平均分概念形成的阶段性,以及伴随而至的符号意识。而概念的学习,从平均分进入除法运算阶段,概念发生了转变。用除号表示平均分,是在不改变先前的知识模块的情况下,增加新知识,但是新旧知识之间存在联系,就是每份同样多,而这也是平均分的数学本质。
(作者单位:潜江市周矶逸夫小学)
责任编辑 孙爱蓉

