LF6铝合金细长轴对称车削加工参数优化*

孙捷夫,孔繁霁,杨 巍

(1.沈阳飞机工业(集团)有限公司，沈阳 110000；2.哈尔滨工程大学智能科学与工程学院，哈尔滨 150000)

0 引言

LF6铝合金属于防锈铝合金，具有轻质高韧等突出优点，同时LF6铝合金还具有良好的焊接性[1]，在航空制造领域中被广泛应用于制造细长轴类连接杆零件，起到传动和减重作用，一般对细长轴类连接杆零件的尺寸精度和表面质量均有较高要求。LF6铝合金细长轴类零件的加工一直是航空制造领域的难点，从结构角度分析，细长轴类零件刚性差导致加工极易变形；从材料角度分析，LF6铝合金塑性大导致表面粗糙度难以控制，同时硬度低进一步加剧加工变形；从工艺角度分析，LF6铝合金属于有色金属，不适于磨削类精加工，只能在数控车床上完成最终状态的实现。

目前关于LF6铝合金细长轴类零件车削加工的研究成果尚无报道，但国内外学者关于细长轴类零件车削加工取得一定进展。文献[2-6]主要通过设计专用装夹定位装置提高细长轴零件加工质量，但需改造机床，缩小机床使用范围；文献[7-11]以误差补偿为主要方法降低切削力等因素的影响，在一定程度上有助于提高细长轴加工质量，但需要额外的动力装置，普遍具有成本高、通用性差等特点；文献[12-17]基于力学分析或车削原理分析优化现有工艺过程提高细长轴车削质量，在理论上具有可行性，但与实际工程应用尚有差距。

基于对现有研究成果的分析，大部分研究成果具有需要专用装置或专用设备、研究目标单一、缺少实际加工基础等特点，且没有针对LF6铝合金材料细长轴的相关研究，无法准确指导实际工程应用。本文以LF6铝合金细长轴的车削加工为研究对象，提出基于专用车夹的对称车削工艺，对车削过程中弯曲变形和表面粗糙度的产生机理进行分析，锁定加工参数是影响加工质量的核心因素，基于中心复合法的车削试验结果进行影响规律分析，基于响应面法进行多目标加工参数优化计算，将优化结果进行实际加工验证其正确性和可行性。

1 对称车削加工模型及理论分析

1.1 加工模型及专用车夹

传统细长轴车削装夹方式一般采用“一夹一顶”、“一夹一拉”“双顶”等，采用上述装夹方式车削加工的本质是通过增加对细长轴的约束提高工艺系统的刚性，但需基于特定机床或专用夹具，尤其对于端面无加工余量或无装夹面积的细长轴零件，上述装夹方法均难以实现。

对称车削加工是将细长轴在常规数控车床上装夹定位，通过将两把车刀以细长轴中心线180°对称分布，基于力学平衡思想提高工艺系统的刚性，进而提高加工精度和表面质量。由于无需额外顶尖尾座，对零件端面结构无特殊限制，对机床选择和细长轴结构形式具有更优的普适性。对称车削模型如图1所示。

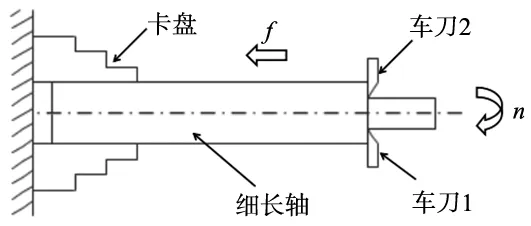
图1 对称车削模型示意图

对称车削实现的关键因素是两把车刀对称分布且同向同速进给完成车削加工。为在常规数控车床基础上无需任何额外设备改造实现对称车削，设计并制造专用车夹，将机床、车刀和零件相连接组成对称车削工艺系统。专用车夹整体结构为阶梯形，端面有刀槽用于放置两把车刀，刀槽内有一中心孔，其孔径大于待加工细长轴零件成品直径，两侧面有螺纹孔，紧固螺栓穿过螺纹孔固定车刀。专用车夹结构示意图如图2所示。

图2 专用车夹实物

基于专用车夹的对称车削按如下步骤操作：

步骤1：调整车夹：在车削加工前，将两把车刀对称安装在专用车夹的刀槽中，按待加工细长轴尺寸调整两把车刀相对专用车夹中心孔的位置后，拧紧调整螺栓；

步骤2：安装车夹：将安装好的专用车夹安装在机床刀塔上；

步骤3：车削加工：通过对刀试切，保证专用车夹中心孔与待加工细长轴中心对应，两把车刀随刀塔按预先设定好的数控程序做进给运动，完成对称车削加工；

步骤4：退刀拆卸：专用车架随刀塔沿机床Z轴正方向水平移动至安全位置，完成加工后拆卸专用车夹。

图3 采用专用车夹的对称车削加工

1.2 弯曲变形力学分析

细长轴的对称车削加工采用三爪卡盘定位夹紧，无顶尖辅助定位的装夹方法。将三爪卡盘一端简化为固定端并限制细长轴全部自由度，对细长轴的约束可简化为轴向力FAx、径向力FAy和弯矩MA，刀具1和刀具2的车削运动分别对细长轴产生轴向切削力F1x和F2x、径向切削力F1y和F2y、主切削力F1z和F2z，考虑各切削力对细长轴加工变形的影响程度，将切削过程中产生的的切削力分解为径向切削力和轴向切削力，而忽略主切削力对变形的影响以简化模型。根据模型约束情况，将细长轴受力模型转化为工程上的超静定梁问题，力学模型如图3所示。

图4 对称车削力学模型

车刀1刀尖点距三爪卡盘端面距离为a，考虑到实际车刀安装误差，设定车刀1和车刀2在细长轴的轴线方向位移差为Δx，则根据静力平衡方程∑MA=0，可得：

MA=F1ya-F2y(a+Δx)

(1)

考虑到实际车刀安装误差，车刀1和车刀2的车削运动分别对细长轴产生径向切削力F1y和F2y之间必然会存在一定差值，设该差值分别为ΔFy则：

F1y=F2y+ΔFy

(2)

根据力学模型边界约束条件，在三爪卡盘装夹处细长轴挠度为零，则可得出细长轴在对称车削时任意一点的挠度曲线近似微分方程：

(3)

式中，EI为细长轴的弯曲刚度，对上式微分方程进行求解，可得出任意点的挠度y的表达式为：

(4)

其中，

基于上述分析，细长轴在对称车削过程中的弯曲变形形态主要取决于两把车刀刀尖的轴向位移Δx，而弯曲变形量大小主要取决于两把车刀的径向切削力的差值ΔFy，通过所设计的专用车夹可保证两把车刀的相对位置，使轴向位移Δx、径向切削力的差值ΔFy均趋近于零，使两把车刀的径向切削力大小近似相等、方向相反，在数值上相互抵消，同时可互相作为辅助支撑增强细长轴的刚性，减小切削过程中其他因素产生的弯曲变形。

因此，基于专用车夹的对称车削细长轴的弯曲变形主要受两把车刀轴向切削力叠加效应和径向切削微小差值的影响，而在零件材料、刀具参数、加工环境既定的情况下，轴向切削力和径向切削力的大小主要取决于加工参数。

1.3 表面粗糙度影响因素分析

细长轴零件表面粗糙度的形成机理可归结为三方面：①车刀切削刃与零件相对运动所形成的几何不平度；②切削力作用下产生的塑性变形或其他物理因素所附加的表面微观不平度；③工艺系统振动所产生的表面振纹。

由对称车削的力学分析可知，两把车刀产生的径向力相互抵消，并互相作为辅助支撑可有效提高工艺系统的刚性，有效避免由振动导致表面粗糙度的形成，而几何不平度和塑性变形是车削加工中无法避免的，仅能通过合理方法使之减小，根据文献[18]可知，通过优化加工参数、切削刀具、切削环境等因素在不同程度上可有效控制零件表面粗糙度，其中加工参的选择对表面粗糙度的影响最大，也是可控性最好的因素。

基于对细长轴零件车削弯曲变形和表面粗糙度分析可知，加工参数的选择对上述两项评价指标均有决定性影响，为对减小细长杆零件车削弯曲变形和表面粗糙度，基于实际切削试验优化细长轴的对称车削加工参数。

2 对称车削试验设计

2.1 试验条件

试料信息：试料材料牌号LF6，材料状态R状态，加工前试料直径20 mm，总长度200 mm。

设备信息：机床选用哈挺GS200型号数控车床，装夹方式为三爪卡盘，冷却方式为乳化液冷却。

刀具信息：刀具材料高速钢，两把刀具的前角8°、后角6°、主偏角85°、副偏角2°、刃倾角12°、刀尖圆弧半径0.2 mm。

加工要求：切削长度150 mm，加工后直径4 mm，最大弯曲变形量小于0.15 mm，表面粗糙度小于Ra0.8 μm。

测量方法：最大弯曲变形量由螺旋测微器在已加工表面的端面为起点，在轴向方向上以10 mm为间距均匀取14个测量点测量，如图5中实线箭头位置，所有测量数据与公称直径之差最大值为最大弯曲变形量；表面粗糙度由表面粗糙度测量仪在已加工表面的端点为起点，取样长度为2 mm，在轴向方向上以30 mm为间距均匀取5个测量区域，并在每个测量区域圆周均布3个测量点测量，所有测量数据均值为细长轴表面粗糙度，如图5中虚线位置。

图5 最大弯曲变形量和表面粗糙度测量方法

2.2 试验方案及试验结果

基于对称车削的原理分析，综合考虑车刀性能和机床参数，初步限定切削速度V的取值范围为200～300 m/min、进给量f的取值范围为0.03～0.1 mm/r、背吃刀量ap的取值范围为0.5～3 mm。

细长轴对称车削试验选用中心复合法进行试验方案设计，中心复合试验法相对传统的正交试验法对变量因子与评价指标之间的非线性关系描述更精确，且中心复合试验法引入旋转因子概念，可突破变量因子的设定界限，能够探究更多的优化解。本试验设定旋转因子为1.287，中心点重复试验次数为2次，试验设计矩阵及试验结果如表1所示。

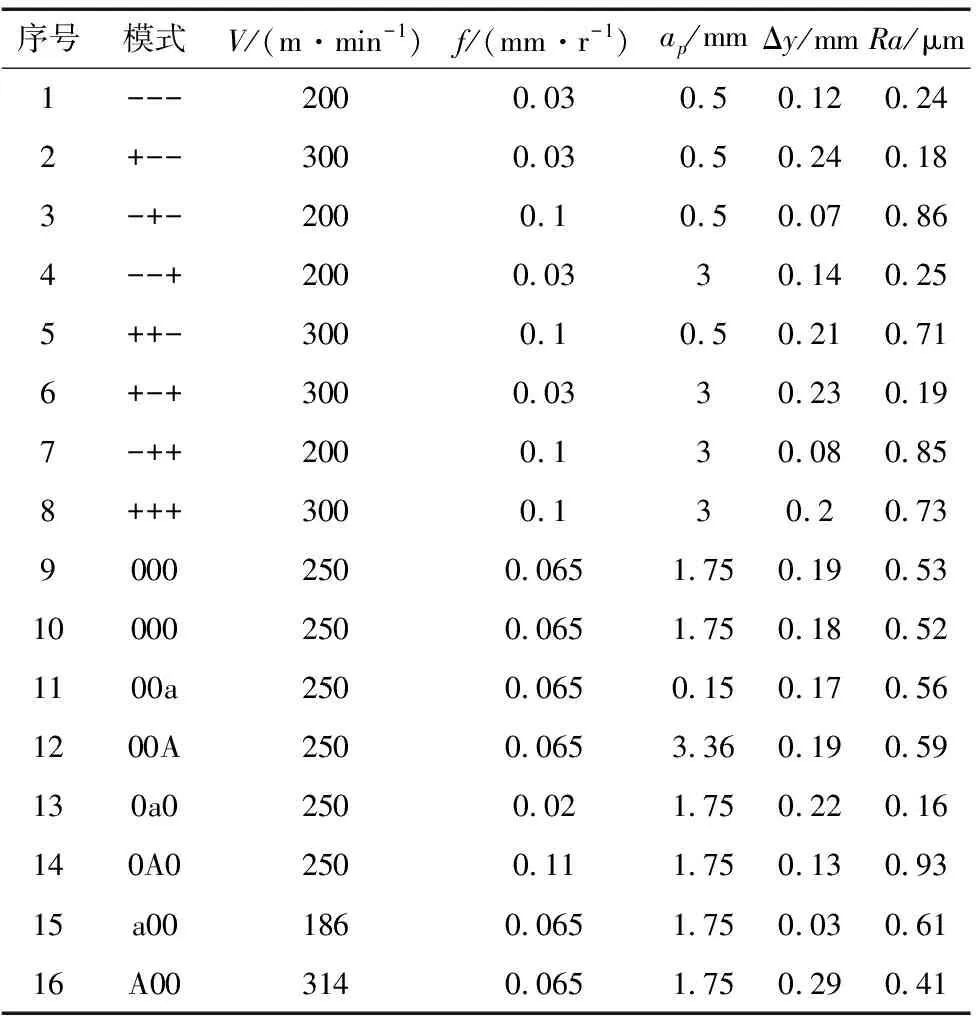
表1 试验设计矩阵及试验结果

表1中模式列“+”“-”分别代表每个因子的立方点，“A”“a”分别代表每个因子的轴向点，“0”代表每个因子的中心点。测量结果Δy表示最大弯曲变形量，Ra表示单次试验平均表面粗糙度。基于表1的试验结果，绘制各加工参数不同水平下的最大弯曲变形量和表面粗糙度趋势图。

由图6可知，最大弯曲变形量受切削速度影响最大，呈正相关；其次受进给量影响较大，呈负相关；受背吃刀量影响较小。由图7可知，表面粗糙度受进给量影响最大，呈正相关；其次受切削速度影响较大，呈负相关；受背吃刀量影响较小。

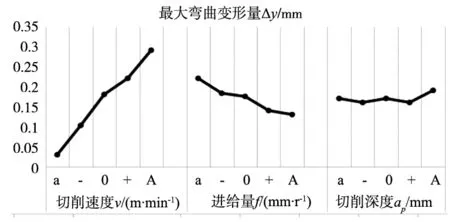
图6 不同水平下最大弯曲变形量趋势图

图7 不同水平下表面粗糙度趋势图

上述现象是由于细长轴刚性差，随着切削速度增大，细长轴自转离心力和切削力综合作用增强，加剧弯曲变形，但切削速度的提高可有效避免刀具表面积屑瘤等现象，有利于表面粗糙度的减小；根据金属切削原理可知，进给量增大使切削厚度相应增大，切屑变形系数减小，整体切削力降低，有利于抑制弯曲变形，但增大进给量会使刀具与细长轴之间切削运动轨迹发生变化，增大切削几何不平度，进而提高表面粗糙度；由于对称车削的双刀具互相补偿效应，降低背吃刀量对切削力的影响，进而弱化对弯曲变形和表面粗糙度的影响。

3 基于响应面法的多目标参数优化

3.1 试验结果统计分析

响应面法是基于多元二次回归方程拟合因素和响应值之间的函数关系，同时兼顾因素之间的耦合影响，具有良好的实际工程应用背景[19]。基于JMP软件采用响应面法对表1中的试验结果进行拟合分析，拟合模型结果如图8和图9所示。

图8 最大弯曲变形量拟合模型“预测值-实际值”图

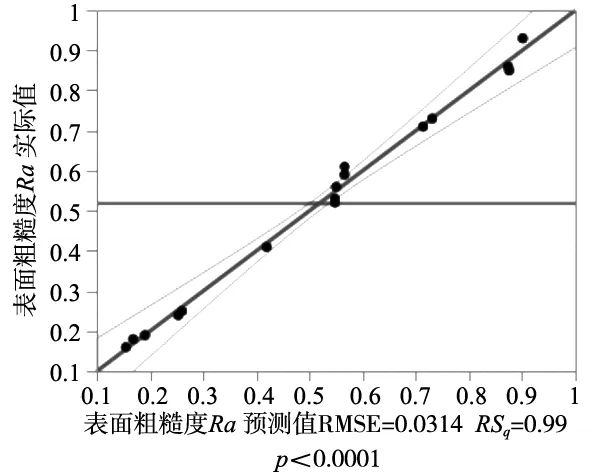
图9 表面粗糙度拟合模型“预测值-实际值”图

由图8和图9可知，最大弯曲变形量和表面粗糙度“预测值-实际值”模型图中数据点均紧密分布于对角线附近，最大弯曲变形量模型R方为0.986，调整R方为0.957,均方根误差为0.042；表面粗糙度模型R方为0.986，调整R方为0.957,均方根误差为0.042，两组模型拟合精度均满足实际工程需要，均具有显著的统计学意义。

图10和图11分别是基于响应面法拟合后最大弯曲变形量和表面粗糙度的各切削用量的各阶变量参数估计值，其中“概率>丨t丨”的值越小表明该因子对结果影响越大，可以看出基于响应面法得出的各加工参数对结果的影响程度规律与极差法所得一致。由图10～图12可知，背吃刀量无论是单因子还是与其他变量的交互相应对最大弯曲变形量和表面粗糙度的影响均不显著。

图10 最大弯曲变形量各阶变量参数估计值

图11 表面粗糙度各阶变量参数估计值

图12 最大弯曲变形量和表面粗糙度综合汇总效应

3.2 加工参数多目标优化

在实际工程中，对细长轴的最大弯曲变形量和表面粗糙度均有要求，以直径4 mm、加工长度150 mm的试料为例，要求最大弯曲变量0.15 mm，表面粗糙度不大于Ra0.8 μm，遵循加工经济性原则，将最大弯曲变量下限设为0.1 mm，表面粗糙度下限设为Ra0.7 μm。

根据上述分析，背吃刀量对最大弯曲变形量和表面粗糙度的影响均不显著，考虑实际加工效率需求，将背吃刀量设定为3 mm，并基于最大弯曲变形量和表面粗糙度的响应面拟合模型，在JMP软件中利用等高线刻画器模块对切削速度和进给量进行多目标优化，如图13所示。

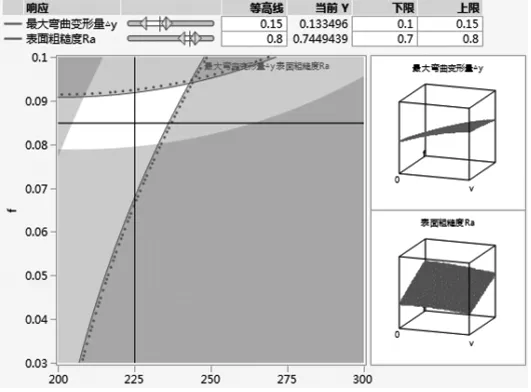
图13 切削速度和进给量的等高线刻画器

图中红色虚线是最大弯曲变形量为0.15 mm的等高线，红色区域为最大弯曲变形量大于0.15 mm或小于0.1 mm的变量取值区域；蓝色虚线是表面粗糙度Ra0.8 μm的等高线，蓝色区域是表面粗糙度大于Ra0.8 μm或小于Ra0.7 μm的变量取值区域；白色部分为同时满足最大弯曲变形量和表面粗糙度要求的变量取值区域，考虑实际加工稳定性和加工效率，在白色区域中心靠右上方处取值，如图13中十字线交汇处，得出最优加工参数为V=225 m/min、f=0.085 mm/r、ap=3 mm，此时预测最大弯曲变形量为0.13 mm，表面粗糙度为Ra0.75 μm。

3.3 实际加工对比验证

为验证基于响应面法所得的最优对称车削参数准确性，进行实际切削加工验证，并分别将图6和图7基于极值法的单目标最优加工参数、以及经验参数作为对比加工验证，结果如表2所示。

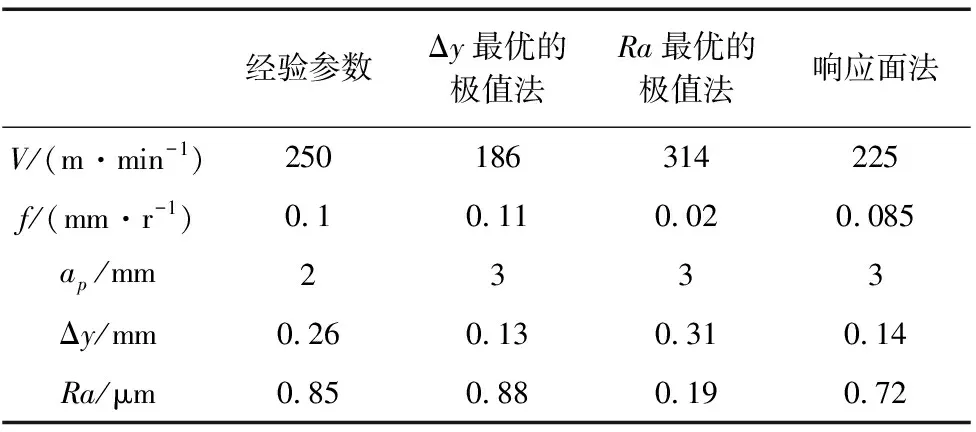
表2 最优参数实际验证结果

经过实际加工验证结果可知，经验参数的最大弯曲变形量和表面粗糙度均不满足要求，而基于极值法单目标加工参数仅能满足单一目标需求，而响应面法实际加工结果与预测值非常相近，且能同时满足两个目标加工需求。

4 结论

(1)通过设计专用车夹实现LF6铝合金细长轴的对称车削加工，基于对称车削力学模型分析和粗糙度形成机理分析，得出：提高LF6铝合金细长轴加工质量的关键是优化对称车削加工参数。

(2)为优化对称车削加工参数，基于中心复合法建立切削试验矩阵，分别利用极值法和响应面法探究加工参数对结果的影响规律，得出：最大弯曲变形量受切削速度影响最大呈正相关，其次受进给量影响较大呈负相关；表面粗糙度受进给量影响最大呈正相关，其次受切削速度影响较大呈负相关；背吃刀量对两项指标影响均布显著。

(3)综合考虑加工质量、加工效率和加工稳定性，在JMP软件中对加工参数进行多目标优化，得出最优加工参数V=225 m/min、f=0.085 mm/r、ap=3 mm，并将优化结果进行实际加工验证，测得最大弯曲变形量为0.14 mm、表面粗糙度为Ra0.72 μm，同时满足最大弯曲变形量和表面粗糙度要求。本文提出的细长轴对称车削工艺可有效指导实际工程应用。