秦岭山前某滑坡稳定性及变形模拟分析

寇甄涛,包 健,杨 贤

(中国电建集团西北勘测设计研究院有限公司，西安 710065)

0 前 言

滑坡作为自然界最常见的地质灾害之一，严重威胁着人民的生命财产安全[1]，同时也制约着区域内的工程建设[2]。因此，采用可靠的手段分析滑坡的形成机理、发育特征和稳定性对滑坡灾害的预判与防治意义重大。

由于自然界中滑坡分布广泛且由来已久，因此对滑坡的研究相对成熟[3]。滑坡评价方法目前可分为定性分析和定量分析[4]。定性分析是通过分析影响滑坡稳定性的主要因素从而判断其失稳的可能性，主要方法包括类比法、图解法等；定量法基于定性法，通过确定数值表征滑坡稳定程度，是目前普遍适用的分析手段。

数值分析方法是近年来新兴的边坡分析方法，该分析手段克服了传统方法无法分析边坡应力应变分布的缺点，并且与实验、理论等方法互补。其计算精度与材料本构模型选取、边界条件设定有关，计算效率高，且成本低，为边坡稳定性分析提供了一种崭新的思路[5-6]。

本文以秦岭山前某滑坡为研究对象，在现场调查与实验的基础上，采用数值计算分析方法分别分析了二维和三维模型的滑坡稳定性，以期对同类型坡体的稳定性分析提供借鉴。

1 工程地质条件及变形机理

滑坡体位于秦岭山前某冲沟左岸，沟道较顺直，右岸有公路通过，交通便利，河谷整体呈不对称的“U型”。沟底基岩裸露，自然坡度40°～55°，滑坡体由碎石土组成，坡度下缓上陡。滑坡后缘“圈椅状”地貌清晰，前缘剪出口明显。滑体平均厚19 m，主滑方向35°。滑床上部为碎石土，下部出露绿泥石片岩。坡体周围岩体完整性较好，除岩体内发育几条小型断层外，无大规模区域断裂通过；区域内地下水类型主要可分为孔隙潜水和基岩裂隙水，根据钻探，地下水位于滑面以下7.5 m，对滑坡稳定性基本无影响。由于滑坡体坡度较陡，在降雨、地震等作用下，滑坡沿基覆界面发生滑动，后缘下坐变形明显。经现场调查，滑坡目前无变形迹象，整体处于稳定状态，暴雨季节前缘有滑塌和变形。主滑方向工程地质剖面见图1。

图1 主滑方向工程地质剖面图

滑坡发育于冲沟左岸，为顺层岩质滑坡。受区域性断裂影响，岸坡岩体破碎，完整性差，植被发育，有利于降水快速下渗进入到岩体结构面及层面中，加速薄层状片岩、层间挤压带泥化和软弱结构面形成。河流在下切过程中，岸坡岩体在卸荷作用下，沿层面拉裂并向临空方向产生变形，受岩体中倾坡外层面切割后，岩体沿层间软弱面拉裂并追踪缓倾坡外的裂隙滑动，最终岩体被剪断，而发展演化为滑坡。

2 二维模型模拟分析

如前文所述，准确判断滑坡的稳定性及变形特征有助于预判其变形趋势。分析计算时，一般按圆弧滑动、平面滑动、折线滑动等方法分析评价稳定性，但上述方法仅可得出稳定系数和条块间作用力，对于坡体变形、应力应变分布分析略显乏力。数值计算方法可有效弥补上述短板，当前岩土界各类数值计算软件如雨后春笋，计算方法日益成熟，已逐渐渗透至科研和生产领域，成为岩土工程分析评价不可或缺的工具。

2.1 模型建立与参数选取

本节采用MIDAS GTS/NX软件分析计算该滑坡，以主滑剖面(图1)为依据建立二维分析模型。在建模时对边坡模型予以必要的简化，考虑到模型建立的便捷性，滑面单元未单独划分网格，而是采用界面单元予以模拟，分析模型如图2，采用强度折减法计算滑坡稳定性。

图2 分析模型示意图

模型参数主要基于试验数据选取，同时类比相近工程经验选取，参数选取见表1。

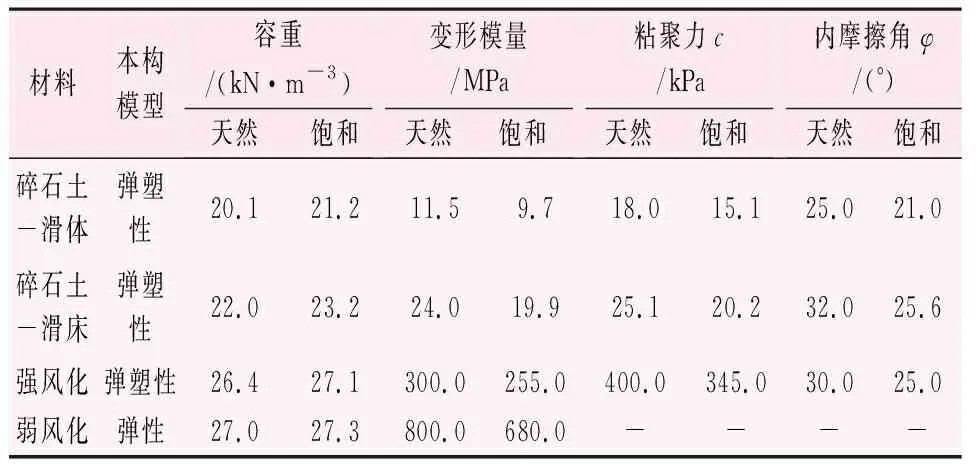
表1 模型材料参数表

2.2 天然工况分析结果

网格赋予天然状态下的物理力学参数后激活计算，计算结果表明该状态下滑坡稳定系数Fs=1.32，根据相关规范[7]中规定，滑坡属基本稳定状态。

采用强度折减法后，岩土体强度参数有所折减，因此重力作用下的位移并非实际变形，但由于强度参数均按相同比例折减，其变形趋势仍可作为变形分析参考，计算完成后的位移如图3、4。

图3 Y方向位移云图

重力作用下，模型沿Y方向垂直向下变形，等值线基本呈平行分布，且越靠近地表位移值越大。位移等值线于滑面处发生突变，滑体内高位移值分布明显多于滑床，最大位移值分别位于滑体后缘处和模型坡顶处，其中坡顶处高位移值由边界效应导致，可不作为评价依据。X方向位移主要集中在滑体中上部，最大值位于滑体后缘，等值线基本平行分布。综上，重力作用下，模型最大变形位于滑坡体后缘处，即坡体失稳时该处最先拉裂，易形成圈椅状后缘。

图4 X方向位移云图

模型应力应变特征是分析坡体变形的重要支撑[8]，如图5、6。模型最大剪应力等值线基本沿平行地表分布，受上覆土压力影响，最大值为776.3 kPa，位于模型底部，最小值为17.5 kPa，位于地表。在滑面处最大剪应力出现较明显的突变，滑体后缘出现高应力富集区，说明在重力作用下，滑体后缘承担着高剪应力，该区域岩土体会优先发生变形破坏。图7为最大剪应变云图，数值计算中，模型的最大剪应变分布可表征滑面形成状态。天然状态下，剪应变主要分布于滑坡体与滑床碎石土中，高应变区域位于滑体与强风化岩体相接处，最大应变值为1.8 cm，滑体后缘处也出现应变累积。

图5 天然工况最大剪应力云图

综上，天然状态下模型最大剪应变区域主要集中在滑面中部，但剪应变区域尚未贯通，因此坡体尚处稳定状态，上述结论与现场调查结果一致。

图6 天然工况最大剪应变云图

2.3 饱和工况分析结果

将模型参数更改为饱和参数，然后激活计算。结果表明，饱和工况下，滑坡稳定系数Fs=0.92，处于不稳定状态。

饱和工况下坡体变形与天然工况相比，滑坡体变形更加明显，以滑面为界形成强烈的变形差异。滑体位移弥散范围更大，最大位移是天然工况下的2.5倍。滑体位移主要集中在后缘部位，以顺坡向变形为主，前缘变形不大，在坡后土体滑移挤压作用下剪出翘起，位移等值线反倾坡内。相对而言滑床岩土体变形很小，除滑床后缘发生小范围变形外，其余部位基本无位移。

最大剪应力分布整体由地表向下逐渐增大，高剪应力在滑体内弥散较广，最大剪应力为651 kPa，位于模型底部，最小剪应力为85.9 kPa，位于地表，如图7，滑面处剪应力值骤增至200 kPa，极易发生剪切破坏。此外，滑体中上部岩土体出现高应力集中区，呈块状、条带状向地表延伸，说明饱和条件下，滑体碎石土的抗剪强度已逐渐无法维持坡体稳定，整体开始出现剪切破坏。

图7 饱和工况最大剪应变云图

图7为饱和工况下最大剪应变云图，与天然工况相比，此时最大剪应变区域已基本贯通，在基覆界面大幅度扩展，最大应变值为6.52 cm。坡面下部也出现了高应变集中现象，说明在重力作用下，滑面处岩土体也发生屈服破坏，大变形导致坡体前缘开始剪出，坡体处于失稳状态。上述结论与位移特征对应。

3 三维模型模拟分析

3.1 三维建模思路

二维模型虽建模简洁，计算快捷，但其本质遵循平面应变假定，并不能体现三维状态下的应力应变情形。本节借助MIDAS的节点导入拟合功能建立三维模型，由于MIDAS软件属数值计算软件，三维建模优势不突出，在面对复杂三维地质模型时并不能准确划分区域，因此需借助其他专业地质建模软件完成。

本文利用GEO-Modeler软件进行优化调整。GEO-Modeler建好地表面和地层界面后分别以点群形式导出，然后在读取软件内修整优化点群分布及密度，以满足建模精度。

最后将优化点群导入数值计算软件拟合建面，并切割分解，从而精确地建立复杂计算模型，数值计算模型如图8。

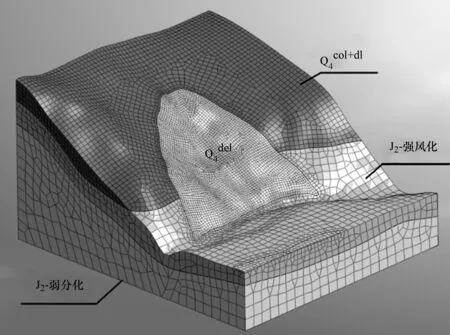
图8 滑坡三维模型网格划分图

3.2 计算结果分析

根据现场调查结论与二维模型分析，天然工况下，滑坡目前处于基本稳定状态，无详细分析必要。本节仅分析饱和工况下三维模型的变形与应力应变，模型参数选取与边界条件设定同上节所述。

三维模型计算得饱和工况下滑坡稳定系数Fs=0.852，较二维计算结果其稳定性更差。重力作用下，Z方向(竖直方向)的变形由地表向下逐渐减小，由坡顶向下位移等值线不规则，如图9，滑体下部位移集中，凸向坡内，说明该段变形较大。Y方向(沿坡面向外)变形如图10，该方向上位移主要集中在滑体中下部，坡顶和基座基本无变形。饱和状态下，滑体中下部已经失稳滑塌，大变形逐渐扩散至坡底，滑体前缘有剪出迹象。

图9 Z方向位移云图(三维) 图

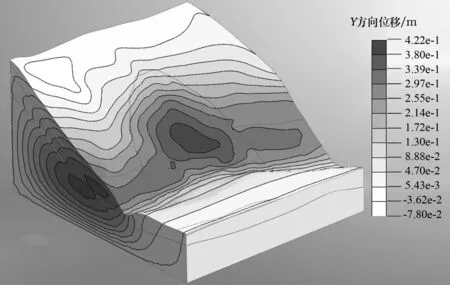
图10 Y方向位移云图(三维)图

滑坡的稳定性很大程度上取决于滑面的屈服程度[9]。在研究三维模型应力应变情形时单独显示滑面单元，如图11、12。饱和工况下，滑面处剪应力在110～190 kPa之间，大值主要分布在滑床碎石土中部，说明滑面该部位容易屈服破坏。最大剪应变也呈相似趋势，高应变值主要分布于滑体与碎石土接触处，坡体前缘也出现了较大的应变值，最大剪应变为4.1 cm，说明此时坡体中部与前缘同时开始屈服破坏，并产生较大应变值，坡体已处于失稳状态，此结论与二维分析结果相符。

图11 滑面最大剪应力分布图

图12 滑面最大剪应变分布图

4 结 论

(1) 滑坡位于秦岭山前某冲沟内，岸坡岩体破碎，降水沿结构面渗入加速了岩体软化。河流下蚀期间，岸坡岩体在卸荷作用下沿层面拉裂变形，受倾坡外裂隙切割后，岩体追踪缓倾坡外的裂隙滑动，最终剪断并形成现状滑坡。

(2) 采用MIDAS数值分析软件对滑坡进行分析计算，二维计算结果表明：自重作用下，滑坡稳定系数Fs为1.32。坡体沿Y方向变形平行地表，X方向的位移主要集中在滑体中上部，最大剪应力值于滑面处出现突变，最大剪应变值集中在滑体中部，但尚未贯通，因此处于稳定状态。

(3) 饱和工况下，二维计算模型Fs为0.92，滑坡处于不稳定状态。相比于天然状态，饱和工况下滑坡变形更加明显，滑体位移弥散范围更大。最大剪应力与最大剪应变值均发生骤增，剪应变区已于坡底贯通，坡体变形剪出迹象明显，已发生整体破坏。

(4) 借助GEO-Modeler软件建立复杂地质模型，在数值计算软件中导入点群准确拟合建面，进而建立三维模型。三维计算结果表明：饱和工况下，滑坡稳定系数Fs为0.852，大变形扩散至滑体中下部，前缘剪出迹象明显，滑床碎石土中部最大剪应力富集，滑体中部与前缘应变值较大，已发生屈服破坏。