三沙湾夏季底边界层动力过程及悬沙输运特征

齐昱恺， 涂俊彪， 于俊杰， 范代读

(1. 同济大学海洋地质国家重点实验室， 上海 200092； 2. 中国地质调查局南京地质调查中心， 江苏 南京 210016)

海湾区域是海陆相互作用的关键带， 有着复杂的地理形态、多重的动力作用、丰富的海洋资源和频繁的人类活动， 使其成为海岸海洋环境研究的重点对象。三沙湾位于福建省东北沿海(图1)， 是福建省面积最大的海湾。三沙湾属半封闭海湾， 仅以东南方向的一个狭口(东冲口)与东海相通， 口门宽度不过3 km； 湾内海域由三都澳、东吾洋、官井洋等众多次一级海湾汇集而成， 是个湾中有湾、港中有港的复杂海湾[1]。

图1 三沙湾区位和水文观测站位图(审图号： GS(2019)3266号)Fig. 1 Location of Sansha Bay and observation sites

三沙湾是我国重要的天然良港和水产养殖基地，但其总体的研究程度仍较低。林航[2]统计分析了湾内霞浦东冲站、宁德城澳站及福安白马站2012年5月至2013年4月实测的逐时潮位资料， 发现湾内均以落潮流为主的潮汐特征。严肃庄等[3]的研究表明三沙湾海域沉积物粗颗粒物质主要是由径流输入的， 细颗粒物质主要由潮流从湾外海域输入。林建伟等[4]基于ROMS模型， 同时考虑温度、盐度和流场以及海表的净热通量、水气通量、动量通量和地表径流， 建立三沙湾精细化水动力数值模型。三沙湾人类活动频繁，主要以网箱养殖为主。Lin等[5]在三沙湾开展了关于网箱养殖对水体交换的影响的研究， 结果表明网箱的存在会减慢海水的运动， 从而改变海湾的水动力格局，减缓湾内外水体交换， 进而影响海湾的泥沙输运。

三沙湾水清沙少， 沉积物再悬浮及输运的过程主要集中在底边界层。底边界层作为海床与海水能量及物质交换的重要场所， 对其动力过程的研究就显得尤为重要。底质沉积物在水流的作用下悬浮进入底边界层， 然后又受到底边界层复杂的水动力条件的影响向上扩散， 当表层悬浮泥沙沉降后经过底边界层又堆积在底床， 这一系列过程能够在底边界动力过程中得到很好地响应[6-7]。因此， 深入研究底边界层动力过程是认识三沙湾沉积动力及悬沙输运的关键。其中， 底切应力是描述底边界层水体混合和泥沙输运的重要参数。本文也将基于现场观测数据对底切应力等关键混合参数进行计算， 探究三沙湾底边界动力过程。

悬浮泥沙是海洋沉积动力研究的一个重要因子，对研究海岸带物质交换和地形地貌变化有着重要意义。本文采用通量机制分解法， 探究三沙湾的悬沙输运机制。利用传统的水文学方法分析处理实测数据， 研究单点测站或断面的悬沙浓度变化是前人研究悬沙输运机制所普遍采用的研究手段[8-10]。Dyer[11]提出了悬沙通量计算公式， 对流速和含沙量进行了平均值和脉动值的分解， 再结合横截面面积，用这三者乘积来表示一个潮周期通过某横断面的悬沙通量。

目前对于三沙湾的水文环境研究更多集中于采用模型探讨其水动力过程， 也有部分集中于水产养殖方面， 但鲜少开展针对湾内泥沙输运格局和机制的研究。本文的工作为进一步研究三沙湾底质再悬浮， 底边界能量物质交换、海岸带工程建设及生态环境保护等有着重要的参考意义。基于2018年夏季在三沙湾海域获得的水文泥沙数据， 结合观测期间水文泥沙时空变化特征， 分析比较了三沙湾底边界动力过程以及悬浮泥沙通量， 探讨沉积物在底边界层动力中的再悬浮情况。

1 方法

1.1 野外观测

2018年8月1—8日先后在宁德三沙湾ND-2站位(中潮， 2日8： 00—3日9： 00)和ND-8站位(小潮，7日16： 00—8日17： 00)进行了现场水文定点潮周期观测， 主要包括流速、盐度、温度、浊度等水文参数的采集。航次调查期间， 天气状况良好， 风浪较小。观测期间， 使用双频测深仪记录水深， 将光学后向散射浊度计Campbell OBS-3A固定在不锈钢架子上，在OBS-3A探头同一高度固定水管口， 并下置铅鱼，通过绞车在各站位每小时拉剖面一次对整个水柱的水文参数进行观测。在表层、中层、底层各停留3～5 min， 并对相应层位抽取一定量的水样， 现场用规格为直径47 mm、孔径0.45 μm的醋酸纤维滤膜进行抽滤， 记录水样体积， 将滤后的滤膜包装好带回实验室进行烘干称重， 计算各水样的悬沙浓度(suspended sediment concentration，CSS)。此外， 流场观测的仪器主要有： ND-2站位， ADCP 600 kHz(坐底三脚架探头朝上， bin size： 0.5 m)、ADCP 300 kHz(海表面浮船探头朝下， bin size： 1.0 m)、ADP(坐底三脚架探头朝下，距底约1.05 m， bin size： 0.04 m， 4 Hz)和ADV(坐底三脚架， 距底0.75 m， 8 Hz)； ND-8站位， 除ADV(坐底三脚架， 距底0.50 m， 32 Hz)的设置不同， 其余仪器设置不变。

1.2 数据分析

1.2.1 底边界层摩阻流速的计算

摩阻流速*u是描述底边界层混合和沉积物再悬浮的重要参数。然而摩阻流速难以直接测量， 通常通过对流速的现场观测计算得到：

其中，0τ为底切应力，0ρ是海水的平均密度。

本文将用前文所述的3种方法估算ND-2、ND-8站位的底边界摩阻流速， 讨论比较各个方法的差异。

1) 直接协方差测量法(COV法)

直接协方差测量法是一种根据摩擦速度*u的定义来直接估算雷诺应力的方法。每个测得的瞬时流速(u、v、w)在无明显波浪影响下都可以进一步分解为2个部分， 平均流速和脉动项(u′、v′、w′)。COV法取决于雷诺应力的直接估算， 与脉动流速的时均量直接相关[12]

在常应力层内， 底应力0τ可以假定近似等于雷诺应力， 结合公式(1)则有：

2) 对数剖面法(LP法)

对数剖面法是利用在常应力层内流速成对数分布的特点来估算摩阻流速*u， 又根据底边界层剪切理论和经验观察， 有：

其中，U为平均流速(m/s)，z为距海底高度(m)，κ≈0.4为卡门常数。

在底床附近的区域， 因流速成对数分布， 所以被称之为对数层， 将上式积分得到对数形式， 即：

其中，z0被称为粗糙长度。通过观测距底不同层位z的流速剖面U， 可以拟合得到摩阻流速*u和粗糙长度z0。

3) 惯性耗散法(ID法)

惯性耗散法利用了惯性子区内湍动能(P)的剪切生成和耗散率(ε)相互平衡的理论关系。本文对ADV采集的流速在各个方向上进行了功率谱分析(图5)，结果表明垂直方向的流速受到噪声影响较小， 且在对数空间内基本吻合–5/3的斜率， 故选取垂直方向的湍流流速功率谱计算湍动能耗散率：

α为Kolmogorov常数取1.56，kw为波数等于根据Taylor冻结假设[13](Taylor's frozen turbulence hypothesis)， 波数谱和频谱存在这样的换算关系：为水平流速的时间平均， 进而计算得到湍动能耗散率ε。

海底边界层内海水的运动被认为是稳定的一维单向湍流运动， 远离湍动能的生成区和耗散区， 即处于惯性子区内， 湍动能的生成和耗散处于平衡状态[14-17]， 得到如下关系：

P与ε两者在理想情况下是相等的， 通过这两者的实际关系可以用来验证数据。

结合公式(3)(COV法)和公式(4)(LP法)， 可得：

1.2.2 拖曳系数的计算

本文还对拖曳系数(drag coefficient，CD)进行了计算。底部切应力与拖曳系数、对应层的平均流速还有水体密度相关

结合公式(1)， 可得

1.2.3 悬沙输运

1) 悬沙浓度反演

本文研究区水清沙少， 在ND-2站位和ND-8站位利用OBS-3A实测时得到的浊度值很小， 某些时刻的测量值甚至小于OBS-3A的测量精度， 得到的数据结果会存在较大误差。Rügner等[18]， Lin等[19]，Grayson等[20]等均认为在低浊度水域， 拟合曲线应是过原点的正比例曲线， 即CSS=mNTU， NTU是浊度单位。研究区表层与底层的悬沙浓度数据在室内分析时存在较大误差与对应层的浊度拟合结果不理想，为了能够更精确地反演悬沙浓度， 本文用中层浊度数据与对应层的悬沙浓度进行拟合，如图2所示。

图2 中蓝色虚线是拟合曲线y=3.132x， 红色和橙色虚线分别是拟合系数95%的置信区间y=2.901x、y=3.362x。

图2 浊度数据拟合曲线Fig. 2 Calibration for the OBS outputs (NTU)

2) 悬沙通量机制分析

悬沙通量是指单位时间内垂直通过某一给定面积的悬沙总量。悬沙通量的机制分解是以研究悬沙通量输运机理为目的， 将悬沙通量分解为若干个动力项， 研究这些动力项对总通量的贡献以及各个动力项所代表的内在机理， 前人对机制分解法已有较多研究， 是一个较成熟的研究分析方法。Dyer[21]将瞬时流速u(x，z，t) 分解为垂向平均量及其偏差项uv之和， 而垂向平均值又可以分解为潮平均项和潮变化项所以瞬时流速u(x，z，t)表达式为：

同理， 瞬时含沙量c(x，z，t)表达式为：

因本文研究站位水深随潮周期变化较大， 将水深h(x，t)也分解为潮平均项h0和潮变化项ht：

则根据悬沙通量的定义， 得到悬沙潮周期Tt平均瞬时单宽悬沙输运通量为：

式中：T为潮周期，——表示垂向平均， 〈〉表示潮周期平均。T1、T2又称为平流输移， 即拉格朗日输移， 反映了单宽潮周期平均水体对单宽潮周期平均悬沙输运的影响；T3、T4、T5反映了涨落潮时水体夹带悬沙的交换现象， 三者共同组成潮泵输移项， 它表示了悬沙的沉降、冲刷与流速间的相位差所引起的输移；T6、T7组成垂向净环流输移项， 与剪切扩散相关[22-23]。

2 结果与讨论

2.1 温度、盐度、悬沙浓度以及流速的时空分布特征

根据仪器观测结果， 在航次观测期间， ND-2站位于三沙湾航道分叉处， 平均水深10.6 m， 潮差5.5 m， 涨潮平均流速0.37 m/s， 最大涨潮流速0.81 m/s， 流向346°；落潮平均流速0.33 m/s， 最大落潮流速0.66 m/s， 流向170°。ND-8站位于三沙湾湾外较开阔海域， 平均水深31.2 m， 潮差4.5 m， 涨潮平均流速0.34 m/s， 最大涨潮流速0.63 m/s， 流向274°， 落潮平均流速0.39 m/s， 最大落潮流速0.81 m/s， 主流向93°。两个站位涨落潮时长基本一致约6小时， 但呈现出涨落潮流速的不对称： ND-2站位涨潮流速大于落潮流速而ND-8站位则相反(图3a、3b)。

两个站位盐度呈现明显的垂直分层现象(图3c、3d)。ND-2站位于交溪河口处， 由交溪带来的淡水与湾外输入的海水相互作用， 使得盐度随涨落潮呈周期性变化。盐度最低值出现在落平潮表层， 最高值出现在涨平潮底部， 整体盐度范围27～32。ND-8站位受到湾内淡水影响较小， 总体盐度相较ND-2站位大，盐度变化范围小， 基本为33～34。

两个站位的温度在垂向剖面上与盐度分布相似(图3e、3f)， 湾内ND-2站位涨潮时低温海水从底部进入湾内， 至涨潮后期水体混合良好， 落潮时层化较为显著。ND-8站位水体温度呈现良好分层， 且未见涨落潮显著差异。

此次研究区域悬沙浓度较低， 通过拟合反演得到整个剖面的悬沙浓度(图3g、3h)。ND-2站位在涨急时， 虽然底层水体流速较小， 但涨潮流先从底层进入带起部分底部沉积物， 导致悬沙浓度升高， 最大值为212.3 mg/L，可影响至距底5 m左右的位置， 5 m以上水体悬沙浓度变化范围在28.5～86.4 mg/L； 但在落急时， 表、中层水体向湾外方向退去， 对水体底部的沉积物作用较弱， 沉积物再悬浮引起的水体悬沙浓度并没有涨急时来的高。而ND-8站位水体的悬沙浓度更低， 最大值109.3 mg/L，底层悬沙浓度高于中层和表层， 在距底5 m以下， 悬沙浓度变化范围较大约在24.7～109.3 mg/L， 由于水深较深，涨落潮时引起的悬沙浓度升高仅能影响距底10 m左右的位置。综上， 三沙湾区域沉积物搬运、再悬浮的过程主要集中在水体近底部， 因此， 本文将对ND-2、ND-8站位的底边界层的相关物理过程进行更深入的研究。

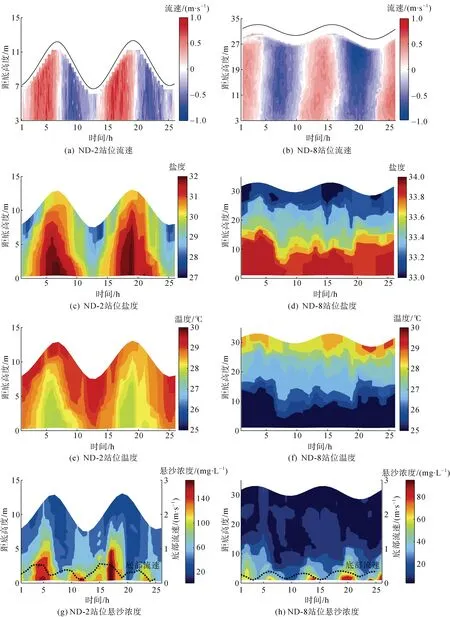
图3 ND-2站位、ND-8站位流速(a、b)、盐度(c、d)、温度(e、f)和悬沙浓度(g、h)的潮周期变化Fig. 3 Temporal variations of vertical structure in current velocity (a， b)， salinity (c， d)， temperature (e， f)， and suspended sediment concentration (g， h) over the tidal cycles at sites ND-2 and ND-8

2.2 底边界层物理过程分析

2.2.1 沉积物再悬浮

将ND-2、ND-8底边界分别为距底0.75 m、0.50 m层的流速与单个潮周期悬沙浓度变化结合(图3g、3h)，在涨落潮流急时底部的水体悬沙浓度明显升高， 沉积物被湍流携带而起， 存在明显的再悬浮， 且2个站位悬沙浓度在单个潮周期内的变化相对于流速的变化存在一定滞后。在高潮位和低潮位时， 底边界层水体流速小不足以搬运沉积物， 此时水体底部悬沙浓度较低。对比ND-2与ND-8站位， ND-2站位的底层流速大于ND-8站位(图3g、3h、4a、4b)， 能够卷起更多的泥沙， 水体也更浑浊。

2.2.2 摩阻流速特征

底应力可以控制沉积物在底床上的再悬浮、搬运及沉积。而底应力的强弱又可以从摩阻流速等物理参数来体现。本文在数据采集时， 在ND-2、ND-8站位坐底三脚架上布放了ADV与ADP， 用于对底边界层物理过程的深入观测。

ND-2站位、ND-8站位ADV采集的流速数据分别为距底0.75 m、0.50 m， 绘制底部流速矢量图可以发现ND-2站位距底0.75 m的潮流为往复流， ND-8站位距底0.5 m的潮流为旋转流(图4c、4d)。另外， 在对两个站位的底边界层流速做功率谱分析时， 发现在三个速度分量谱中在对数坐标下存在–5/3斜率。其中， 垂直方向的流速功率谱斜率最接近–5/3理论斜率， 其受到环境噪声影响较小， 同时这也标志着惯性子区间的存在(图5)。

图4 ND-2站位(a、c、e、g、i)、ND-8站位(b、d、f、h、j)底边界水平流速流速、流速矢量、雷诺应力和摩阻流速潮周期变化Fig. 4 Temporal variations in the horizontal velocity， current vector， Reynolds stress， and friction velocity over the tide cycles at (a， c， e， g， and i) ND-2 and (b， d， f， h， and j) ND-8

图5 ND-2站位(a)、ND-8站位(b)底边界层速度分量功率谱Fig. 5 Power spectrum of the 3D velocity components at (a) ND-2 and (b) ND-8

1) COV法

用COV方法可以直接估算ND-2、ND-8站位底边界的雷诺应力(图4e、4f)。结果显示， ND-2站位与ND-8站位的雷诺应力与该点位的平均流速存在较好的正相关性， 流速大时雷诺应力也相对较大； 从整体来看， ND-2站位的雷诺应力大于ND-8站位， 又根据得到两个站位的摩阻流速， ND-2平均值为0.016 m/s， 最大值为0.030 m/s； ND-8平均值为0.012 m/s， 最大值为0.027 m/s。

2) LP法

经过对ADP的流速数据(距底1.05 m)处理后发现， ND-2、ND-8站位底边界层的流速符合对数分布(图6)， 故可利用LP方法求得两站位的摩阻流速。在对数拟合过程中， 为了能够得到更精确的摩阻流速， 计算时挑选了拟合相关系数R2＞0.98的时刻数据。对比ND-2与ND-8站位， 湾内的ND-2站位摩阻流速曲线的起伏波动较湾外ND-8的小。用LP方法求得ND-2站位底边界层摩阻流速平均值为0.021 m/s， 最大值0.053 m/s； ND-8站位底边界层摩阻流速平均值为0.024 m/s， 最大值0.062 m/s(图4g、4h)。

图6 ND-2站位(a)、ND-8站位(b)底边界流速对数层拟合结果Fig. 6 Logarithmic layer fitting curve for the measured velocity at (a) ND-2 and (b) ND-8

3) ID法

ND-2、ND-8站位底边界湍动能的产生和耗散存在如图7的关系， 其中P是通过雷诺应力计算得到(式7)，ε是根据功率谱中的斜率计算得到(式6)， 两个站位的P与ε处于相对平衡的状态。根据式8可以得到ND-2与ND-8站位的摩阻流速(图4g、4h)。结果显示， 在潮周期内图像连续且随着涨落潮流速变化， 摩阻流速也发生相应的变化， 在ND-2站位， 底边界层摩阻流速的平均值为0.015 m/s， 最大值0.028 m/s； ND-8站位， 底边界层摩阻流速的平均值为0.014 m/s， 最大值0.027 m/s。

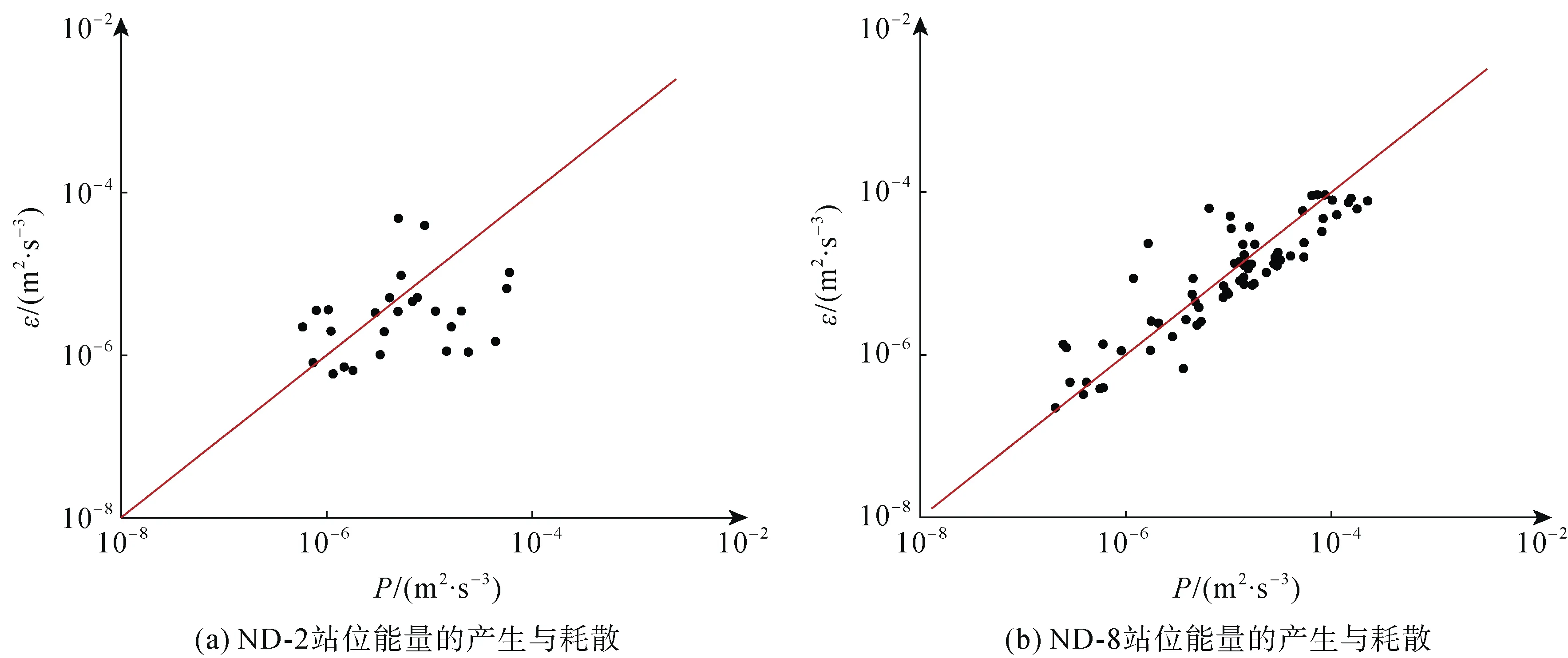
图7 ND-2站位(a)、ND-8站位(b)能量产生与耗散Fig. 7 Scatter plots of the turbulent kinetic energy production (P) and dissipation (ε) at (a) ND-2 and (b) ND-8

对比两个站位用3种方法估算的摩阻流速， 结果为LP法估算的摩阻流速最大， COV法与ID法的估算结果相近， 这与Sherwood等[24]得到的结论类似。LP法通常应用于稳定且发育良好的底边界层中， 流速通常符合对数分布规律[14]， 对数据的拟合相关性要求较高， 较低的拟合相关性会对计算结果有巨大影响，这种方法容易受水体层化或底床变化的影响[25]。本文选取R2＞0.98的数据， 故可以忽略数据上对计算结果造成的误差； 另外， Kim等[26]认为沉积物分层也会影响LP法的估算结果； 另一误差来源是， 分析计算时，通常假设底床位置不变， 在动力较强区， 底床会在潮周期内发生变化， 在此情况下若仍使用z=0的固定位置， 势必会造成误差。根据上述误差来源分析ND-2，ND-8站位可能存在的情况， 在湾内的ND-2站位主要受到潮汐作用的影响， 波浪的对底床形态的影响可忽略不计， 而该站位悬沙浓度较高， 影响结果误差的主要因素很可能是沉积物分层； 处于湾外的ND-8站位悬沙浓度较低， 受到潮汐和波浪的共同作用， 底床形态的变化可能是计算结果误差的主要原因。COV法的估算结果在靠近底床时更加准确， 更适用于恒应力层摩阻流速的计算[26]， Voulgaris等[27]和Trowbridge等[28]用COV方法计算大陆架海域摩阻流速取得了较为精确的估计值。与LP法不同， COV法并不依赖测量点距底的高度， 误差主要来源于观测时仪器是否发生倾斜或是否收到次生流的影响， 本文中ND-2站位与ND-8站位摩阻流速的结果与流速成正相关关系， 推测观测时底部水体混合均匀处于恒应力状态。ID法基于惯性子区内湍动能的产生和耗散之间平衡的理论关系， 来估算底边界层摩阻流速， 该方法已广泛应用于海洋底边界层的研究[28-29]。因此， 湍动能的产生区和耗散区是否充分分离以及底部沉积物分层是否会扰乱湍动能产生和耗散的局部平衡是ID法估算结果的主要误差来源。Kim等[26]认为因悬浮泥沙分层导致的产生与耗散的扰乱， 可能会使最后的估计值偏小10%， 结果显示ID法的估算结果较准确。本次研究中，利用COV法和ID法求得两个站位的摩阻流速接近，且误差较小， LP法的估算结果存在较大误差， 为了让误差最小化， 尽可能避免3种计算方法适用条件造成的局限， 故舍去LP法的估算结果， ND-2站位与ND-8站位取COV法与ID法计算结果的平均值作为该站位的摩阻流速(图4i、4j)。ND-2站位摩阻流速平均值为0.016 m/s， ND-8站位摩阻流速平均值为0.013 m/s。

拖曳系数也是一个能够反映底边界层泥沙输运情况的重要物理参数。根据公式(10)， 可以得到两个站位的拖曳系数。但在计算时， 由于在流速小于0.1 m/s的情况下， 仪器在收集数据时会受到噪声干扰， 以至于得到数据无法检验湍流行为[30]， 进一步计算会导致计算结果误差较大。本文ND-2站位中所有时刻的流速频谱符合–5/3斜率， 但ND-8站位存在50个时刻的流速惯性子区间被噪声干扰受到限制[31-32]， 图像斜率并不符合–5/3斜率， 所以舍去后对剩余100个数据进行结果拟合。从最后的拟合结果(图8)中可以发现，ND-2站位距底0.75 m的拖曳系数约为2.03×10–3，ND-8站位距底0.50 m的拖曳系数约为2.03×10–3， 两个站位的0.75 m层与0.50 m层的拖曳系数几乎相等， 可以推断出ND-2站位的底边界切应力大于ND-8站位。

图8 ND-2站位(a)、ND-8站位(b)拖曳系数Fig. 8 Drag coefficient of (a) ND-2 and (b) ND-8

2.3 悬沙输运机制分析

运用公式(14)对ND-2、ND-8站位的潮周期平均单宽悬沙输运量进行计算， 结果如图9和表1。其中，T1—T7分别表示不同动力因素相关的通量项，Tsum为净输运通量， 正值表示沿主流速方向向内(向湾内)， 负值表示沿主流速方向向外(向湾外)。从图中可以看到， 三沙湾悬沙整体从湾外向湾内方向输运， ND-2站位潮周期平均单宽悬沙输运强度为74.88 g/(m·s)， 远大于ND-8站位10.57 g/(m·s)， 两个站位的输沙强度受到不同动力因素的影响， 在ND-2站位平流输沙项(T1、T2)占主导作用， 潮泵输沙项(T3、T4、T5)次之， 垂向净环流输沙项略有影响； ND-8站位平流输沙和垂向净环流输沙是主要影响因素，潮泵输沙几乎无贡献。

图9 ND-2站位(a)、ND-8站位(b)潮周期平均单宽悬沙通量Fig. 9 Tidally averaged fluxes per unit width at the observation sites： (a) ND-2 (a) and (b) ND-8

表1 单宽输沙量绝对值的贡献率(%), 沿流速主方向向湾内为正Tab. 1 Contributions of different sediment transport parameters to the magnitude of absolute sediment transport (%),positive toward the bay along the main direction of the velocity

欧拉余流输沙项(T1)和斯托克斯漂移输沙项(T2)构成平流输沙项， 又称为拉格朗日余流输沙项。其大小与余流和潮周期平均悬沙浓度密切相关。ND-2与ND-8站位在观测期间，T1均大于T2， 这使得平流输沙项的方向主要由T1决定。在ND-2站位，T1与T2方向相同， 均向湾内方向， 两者加强了悬沙向湾内输运；在ND-8站位，T2抑制悬沙向湾内输运， 其方向与T1相反， 平流输沙方向向湾内。ND-2站位平流输沙强度为62.83 g/(m·s)， ND-8站位为20.58 g/(m·s)。

潮汐与悬沙浓度潮变化项(T3)、潮汐、潮流与悬沙浓度潮变化项(T4)、潮流与悬沙浓度潮变化项(T5)共同组成潮泵输沙， 由于涨落潮挟沙量不同， 导致底部沉积物在潮周期内不对称输移， 并且其产生的滞后效应使得悬沙浓度与流速存在一定的相位差，从而在潮周期内悬沙发生净输移。ND-2站位T3和T4作用较小，T5的贡献占主要， 且悬沙向湾内方向输运，输沙强度为49.25 g/(m·s)。而在ND-8站位， 潮泵输沙项几乎为0， 输沙强度为0.78 g/(m·s)。张钊等[33]认为在涨潮悬沙浓度明显大于落潮的潮周期里，T5向陆输沙， 在涨落潮悬沙浓度相差无几的潮周期里，T5输沙强度较弱。

重力环流贡献项(T6)与流速与含沙量潮变化垂向剪切相关项(T7)组成垂向净环流输沙项。由于在垂向上， 各层余流的不一致和悬沙浓度分布不均匀， 导致在潮周期内各层输沙量叠加后不能相互抵消， 从而产生悬沙的净输移， 不难得出， 垂向环流输沙项的强度与垂向余环流和悬沙垂向分布情况紧密相关。在观测期间两个站位的垂向净环流输沙项并不高都向湾外输沙， 其中的T6项均为主要贡献项， ND-2站位垂向净环流输沙项强度为–31.24 g/(m·s)， 在ND-8站位垂向净环流输沙项强度为–10.79 g/(m·s)。

三沙湾地区主要受到潮汐的影响。平流输沙方向主要受余流的控制， 根据资料三沙湾夏季余流方向北， 导致ND-2及ND-8站位的平流输沙向湾内。Yu等[34]认为潮泵作用引起的悬沙输运主要是海流不对称及泥沙滞后效应引起的。在ND-2站位潮差较大，涨落潮流呈现明显的不对称性， 从而导致了潮泵输沙整体向湾内。ND-8站位流速呈旋转流特征， 而机制分解法潮泵输沙项对往复流的响应明显， 在ND-8站位潮泵输沙贡献率低可能是旋转流导致了悬沙横向输移。

3 结论

1) 三沙湾潮汐类型为正规半日潮。湾内ND-2站位温盐特征明显受涨落潮影响， 表现为涨潮时水体呈低温高盐， 落潮相反； 位于湾外的ND-8站位水体层化明显且基本不受涨落潮的影响。三沙湾水域悬沙浓度总体较低， 并呈现出底层聚集和随流速变化的特征， 表明再悬浮作用起主导作用。

2) 位于湾内的ND-2站位近底层悬沙浓度湾外ND-8站位高。通过计算发现ND-2站位底切应力较ND-8更大， 因此判断为潮致切应力主导下的底部再悬浮导致ND-2悬沙浓度更高。

3) 悬沙通量机制分解表明， 三沙湾夏季中潮与小潮期间的潮周期单宽悬沙从湾外向湾内方向净输运， 在ND-2站位平流输沙项占主导作用， 潮泵输沙项次之， 垂向净环流输沙项略有影响； ND-8站位平流输沙和垂向净环流输沙是主要影响因素， 潮泵输沙几乎无贡献。

致谢： 参与外业调查的还有阮得卫， 江彬彬， 任发慧， 李健成， 孙飞翔，一并表示感谢。