第三轨中间接头不平顺阈值研究

阮杰，郭文，魏国梁，徐鸿燕，阎晓晖

(1.武汉理工大学 现代汽车零部件技术湖北省重点实验室，湖北 武汉430070；2.中铁第四勘察设计院集团有限公司 电化院，湖北 武汉430063；3.武汉地铁运营有限公司，湖北 武汉430035)

第三轨受流系统在城市轨道交通中被广泛应用。第三轨受流器动态接触力的变化情况直接影响轨道车辆受流质量的高低[1]。为保证电力机车良好受流，靴轨接触压力要保持在一定范围内，接触压力过大会增加靴轨接触面的异常磨损缩短其使用寿命[2−3]；接触压力过小易发生靴轨离线，引发电烧蚀[2,4]。然而，我国对第三轨受流系统许多工程实际问题尚未有较为完善的解决方法，如靴轨拉弧、硬点(弓网系统接触线局部刚度变化引起接触力改变的现象)处冲击控制等。基于此，研究第三轨硬点区域靴轨系统的动态特性，提出中间接头不平顺的安全阈值，以期减小硬点冲击及降低靴轨离线率。目前，国内外学者采用工程试验和计算机动态仿真的方式研究靴轨系统相互作用。GREEN等[5]设计了能够实时检测靴轨动态特性的测试系统，基于测试数据实现对靴轨离线位置进行定位。WESTON等[6]通过靴轨动态特性试验所测量的动态接触力、滑靴位移以及扭簧扭矩等试验数据，明确了影响靴轨系统振动的主要因素。DONG等[7−8]使用研制的载流摩擦磨损试验装置，研究了法向压应力和电极性对靴轨摩擦副之间载流摩擦磨损特性的影响。JINFA等[9]通过靴轨系统动力学仿真，基于靴轨动态接触力和振动加速度建议列车最大运行速度120 km/h。张鹏飞[10]以磁浮列车靴轨系统为研究对象，探究静态接触力、膨胀接头不平顺及跨距对靴轨系统接触振动的影响，并选取上述参数最优组合方案以改善靴轨动态受流质量。综上所述，诸多学者的研究成果为轨道交通受流系统的设计和研究提供了丰富的理论和试验指导，但对第三轨硬点来源的判断以及硬点区域靴轨动态接触力的变化规律等方面的研究存在不足。本文通过工程试验和仿真计算相结合的方式研究靴轨系统动态特性，探究了靴轨冲击的来源及其特性，并分析了第三轨中间接头不平顺的阈值。首先，对武汉地铁某线使用的靴轨系统开展了试验研究，明确了接触力冲击脉冲峰与第三轨局部不平顺之间的联系。然后，建立含不平顺接头的靴轨有限元模型，以研究硬点区域靴轨系统的动态特性。最后，研究不同高差接头激励下接触力变化，分析第三轨中间接头不平顺的阈值。

1 受流器/第三轨系统动态特性试验

1.1 测试原理及测试系统组成

目前，靴轨动态接触力不能通过仪器直接测量得到，通常是通过测量力传递路径上的力或变形量间接获得。根据武汉地铁下接触式受流器的结构特点，通过在摆臂粘贴应变传感器测量摆臂处应变，并结合滑靴底部安装加速度传感器的测量值间接测量靴轨接触压力，具体测量模型与参数标定过程参考文献[11]，其中动态接触力测量模型如图1所示。

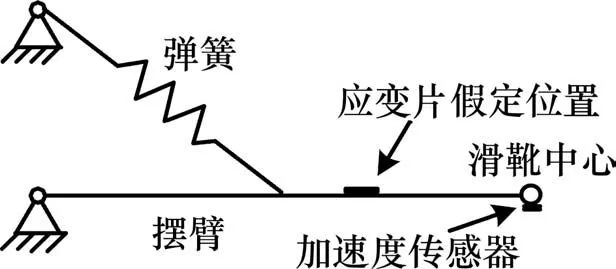
图1 动态接触力测量模型Fig.1 Dynamic contact force measurement model

本次试验在武汉地铁某线试验线路直线区段(含一处断口)以20，30和40 km/h 3个速度进行往返测试。采集6组测量数据。其中测量系统数据转换、采集和记录设备如图2所示，安装测量系统后的测试受流器如图3所示。

图2 测量系统数据转换、采集和记录设备Fig.2 Data conversion,acquisition and recording equipment of measurement system

图3 安装测量系统后的测试受流器Fig.3 Test current collector after installation of measurement system

1.2 测试结果分析

靴轨动态接触力是由应变测量分量经过动态惯性力修正得到，之后采集数据通过低通滤波，图4为40 km/h上行应变测量分量、动态惯性力及动态接触力结果，图5为40 km/h下行动态接触力结果，40 km/h上行动态接触力统计结果见表1。测量结果显示，靴轨相比于弓网其接触力状态存在显著差异，在局部存在冲击尖峰。

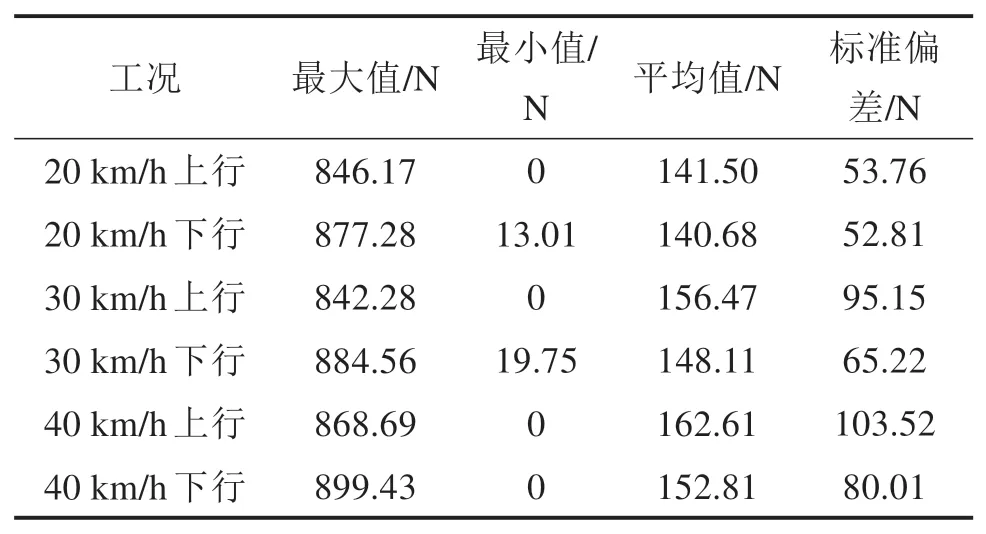
表1 40 km/h上行动态接触力测量统计结果Table 1 Statistical results of dynamic contact force in posi‐tive direction at running speed of 40 km/h

图4 运行速度40 km/h上行测试结果Fig.4 Test results of running speed 40km/h in positive direction

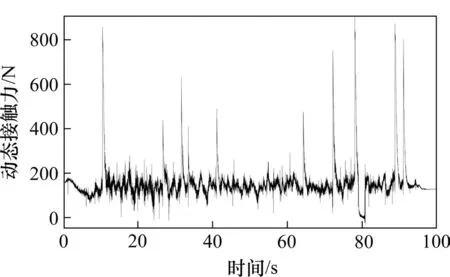
图5 运行速度40 km/h下行动态接触力Fig.5 Dynamic contact force in opposite direction at running speed of 40 km/h

40 km/h上行和下行测试结果对比显示，受电靴通过供电轨相同位置处动态接触力数据的波形、波峰及下降沿相似，仅部分幅值存在差异，故以较恶劣的上行作为研究工况。从靴轨动态测试结果及各指标统计值可知：动态接触力的平均值、标准偏差随车速增加而增大，表明靴轨间振动情况更加剧烈；动态接触力的最值受采样频率、滤波频率等因素影响，其数值大小仅作为参考；表中统计的最小值发生于断口处，正常运行线路上记录的接触压力显示无大于0.1 s的离线，视频中也未见明显火花；在测试车速范围内，多数区域应变测量分量起主导作用，且受车速影响较小；在少数“硬点”位置，动态惯性力起主导作用，造成动态接触力显著增大；动态接触力的表现为“硬点”位置有较大的冲击幅值，导致靴轨动态接触力的平均值、标准差相比典型弓网接触力都偏大。

综合分析，靴轨动态接触力与弓网典型接触力不同，靴轨动态接触力呈现在非硬点区域波动平稳，在硬点区域局部高冲击的形态。

1.3 “硬点”的定位与冲击峰来源判断

测量结果显示以加速度信号突变指示的“硬点”位置对应于接触轨的位置相对固定。因此，基于采集数据判断“硬点”存在的位置并分析其原因。

硬点处接触力的尖峰是在动态惯性力分量中出现，考虑到车速波动的误差，以断口为基准考察附近的“硬点”定位较为准确。关注过断口后的3个尖峰位置，将其标记为1，2和3，分别计算尖峰距断口的距离，作为测试线路的现场观测点，寻找“硬点”在实际线路的位置。尖峰标记如图6所示，距离计算结果如表2所示。

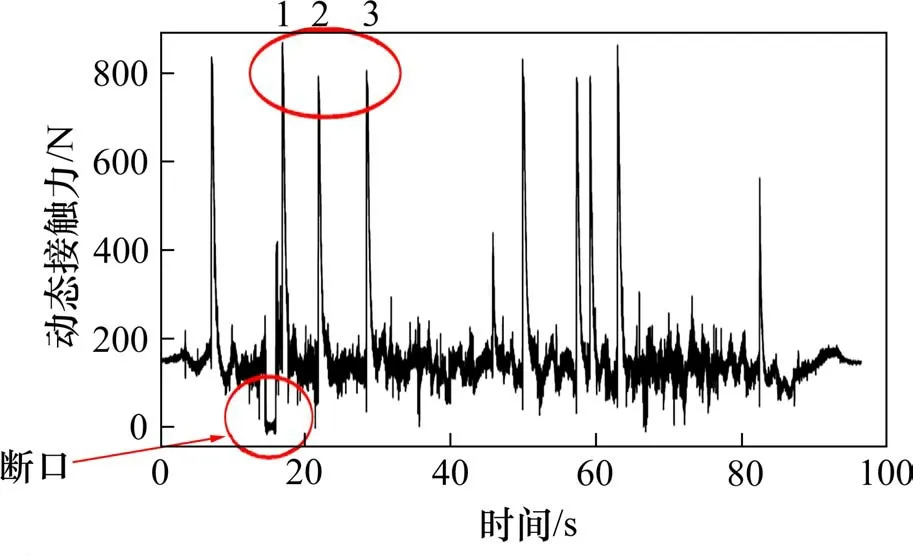
图6 动态接触力显示的断口后3个硬点Fig.6 Three hard points after fracture shown by dynamic contact force

表2 硬点距断口距离Table 2 Distance between hard point and fracture

现场观测上述位置的供电轨，发现都有第三轨中间接头。接头两侧接触轨受流面手触明显存在台阶。低侧有大量碳粉，高侧有明显的磨痕且无碳粉。如图7所示。

图7 硬点位置现场观测结果Fig.7 Field observation results of hard spot position

图8 为200 m和230 m处的接头。这2处接触压力测量结果未显示硬点存在，实际观察接头表面触感过渡平滑，碳粉均匀分布于接头两侧，因此推断接触力冲击峰的来源并不是“硬点”代表的局部刚度变化，而是局部不平顺的结果。

图8 未出现“硬点”处现场观测结果Fig.8 Field observation results without hard spots

2 含不平顺接头冲击模型的建立

2.1 含不平顺接头的第三轨有限元模型

第三轨中间接头用于相邻接触轨的机械和电气连接，由于接触轨制造误差及安装误差造成中间接头安装完成后，前后接触轨受流面存在高度差。为研究不平顺接头激励下靴轨系统动态特性，建立含不平顺接头的第三轨有限元模型。将第三轨支持结构和接触轨耦合，得到含不平顺接头的第三轨有限元模型。取中间接头前后各2 m作为仿真区段，不平顺接头高度差为0～0.5 mm。含不平顺接头的第三轨有限元模型如图9所示。

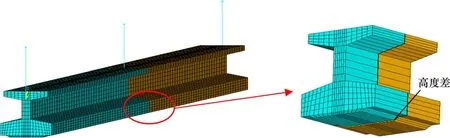
图9 含不平顺接头的第三轨有限元模型Fig.9 Finite element model of the third rail with irregularity joint

2.2 受流器归算质量模型

借鉴受电弓归算质量模型[12−13]等效方法，根据能量守恒原理将受流器机构等效成若干集中质量构成的归算质量模型，通过弹簧和阻尼器连接各当量质量块。本文用于靴轨仿真的受流器模型，采用二质量/弹簧/阻尼系统，如图10所示。质量块m1为滑靴的等效质量；质量块m2为受流器其他机构的等效质量。

受流器的动力学平衡方程如下：

其中，二元质量模型各矩阵如下：

式中：Fc为作用在滑靴的接触压力；F0为受流器静态接触压力；y1与y2为质量块的垂向位移；m1与m2为受流器的等效质量；c1与c2为受流器的等效阻尼；k1与k2为受流器的等效刚度。

2.3 非线性阻尼的模拟

受流器是由固定部分、摆动部分、转轴和弹簧组成。其中固定部分包括安装底座和阻尼减震器;摆动部分包括摆臂、受电靴支座和受电靴。其固定部分和摆动部分的连接方式决定受电靴在与第三轨接触上下波动过程中，当量质量、连接刚度等参数都与受电靴抬升位置有关。根据受流器结构特性分析，其阻尼特性必须采用非线性模型模拟。

受流器的阻尼器阻尼大小和质量块相对运动速度相关。可将其波动上升和下降方向的阻尼简化为定值，第二阻尼c2可表示为：

c21，c22分别为受电靴上升沿阻尼和下降沿阻尼。

2.4 靴轨耦合计算模型

靴轨动态受流过程中，两者的接触位置和接触状态随受流器运行时间发生变化，因此靴轨耦合系统具有强烈的时变性及非线性。本研究基于有限元方法求解靴轨耦合系统动力学问题，求解算法采用中心差分法。靴轨耦合有限元模型的建立过程如下：

1)建立含不平顺接头的第三轨有限元模型；

2)建立考虑滑靴表面形貌的二质量受流器模型；

3)通过接触单元连接受流器与第三轨，接触算法采用罚函数法，靴轨系统接触压力计算公式如下：

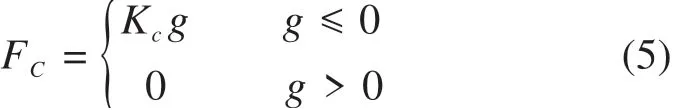
式中：Fc为接触压力；Kc为接触刚度；g为接触对在接触面的法向间隙。

按上述步骤含不平顺接头的冲击模型如图11所示。

图11 含不平顺接头的冲击模型Fig.11 Impact model of joint with irregularity

3 结果分析

3.1 模型验证

动态接触力测试数据显示低速时接触力测量值相较平稳，冲击峰不明显。根据不平顺接头处高度差实测值，取接头前后各2 m区段，接头高度差为0.2 mm，受流器静态接触压力为120 N，加载速度分别为30 km/h和40 km/h，进行靴轨耦合系统动力学仿真。仿真结果与试验结果对比如图12所示。

由图12可知，动态接触力仿真数值及变化规律与试验结果有较好的一致性，滑靴通过不平顺接头时受到局部高冲击，中间接头前后接触力波动平稳。关注过断口后的第2个不平顺接头(尖峰)位置，分别将其编号为1和2，统计各工况下滑靴通过该中间接头时的动态接触力最大值和接触状态，对比结果见表3。

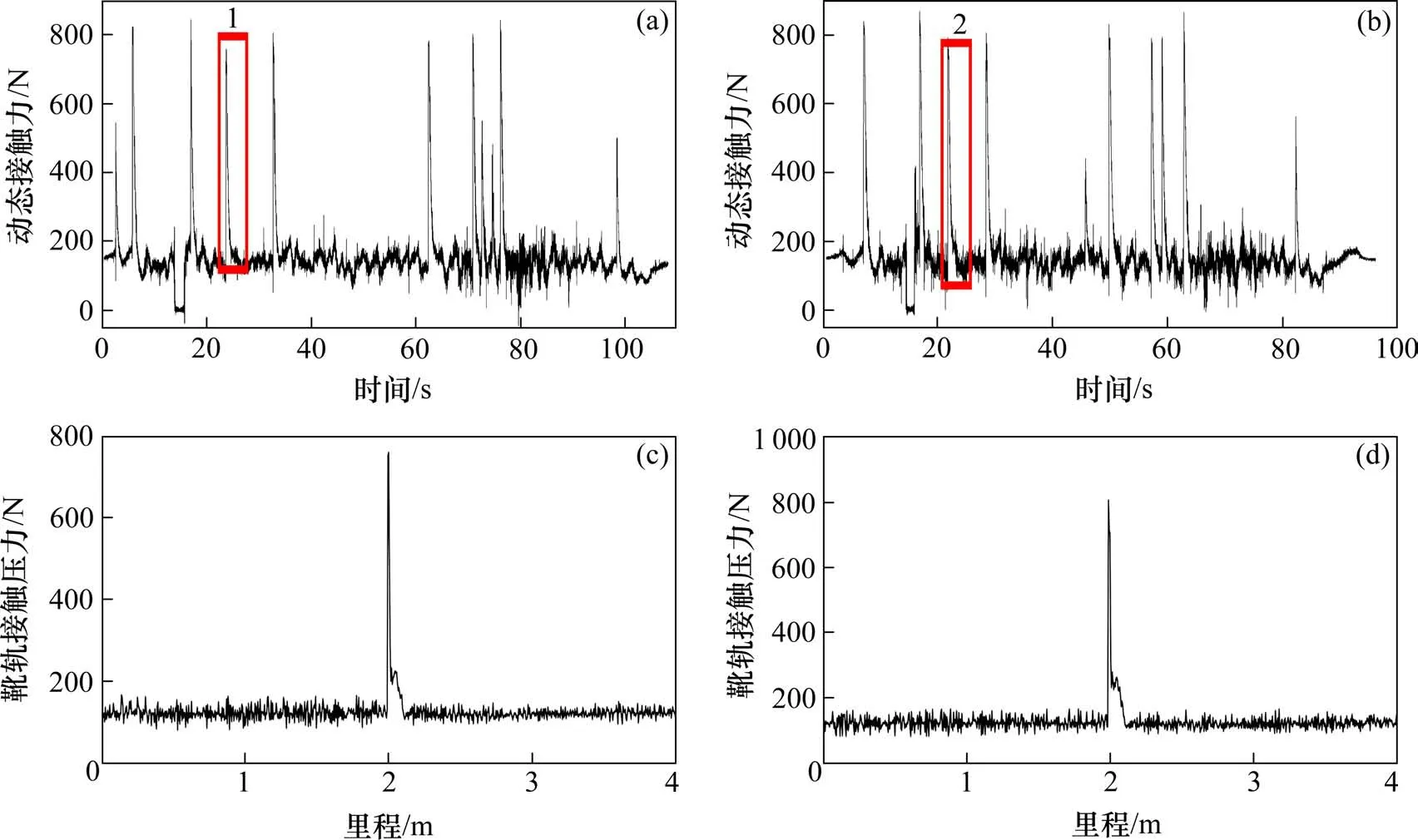
图12 试验结果与仿真结果对比Fig.12 Comparison of test results and simulation results

由表3可知，各工况下动力学仿真结果与试验结果较为接近，30 km/h工况下接触力最大值误差仅为1.35%，靴轨接触状态显示均未发生离线，表明本研究建立的含不平顺接头的冲击模型是有效的。

表3 各工况下试验结果与仿真结果对比Table 3 Comparison of test results and simulation results under various working conditions

3.2 不平顺接头高度差的影响

为探究不平顺接头高度差对靴轨动态受流质量的影响，取不平顺接头前后各2 m区段，接头高度差分别取0～0.5 mm，受流器静态接触压力为120 N，受流器加载速度为100 km/h，进行靴轨耦合系统动力学仿真，结果如图13所示。对不同接头高度差下的靴轨动态接触力及离线时间作统计性描述，统计结果如表4所示。

由图13可得，运行速度一定时，受流器通过不平顺接头时受到的冲击随接头高度差的增加而增大；接头高度差为0 mm时，整个分析区段内靴轨接触压力在70～170 N间平稳波动，无局部冲击现象；接头高度差为0.1 mm时，中间接头附近的动态接触力波动明显加强，但未发生靴轨离线；当高度差超过0.2 mm时，滑靴通过不平顺接头时受到的冲击及通过接头后的动态接触力波动更加剧烈。

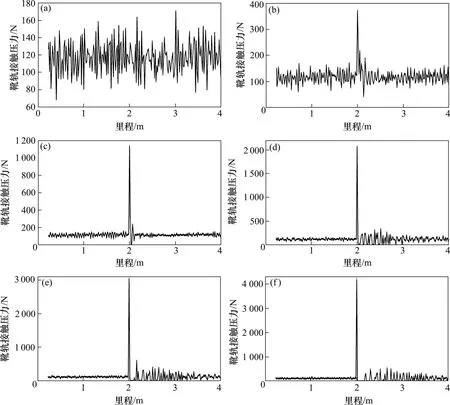
图13 不同高度差下动态接触力Fig.13 Dynamic contact force under different height difference

由表4可知，靴轨接触压力最大值、一次离线时间及离线时间总和随不平顺接头高度差的增加而增加；当高度差0～0.2 mm范围内时，动态接触力最小值大于0 N，靴轨未发生离线；当高度差在0.3～0.5 mm范围内时，靴轨发生离线且二者间振动不断加剧，靴轨动态受流质量变差。

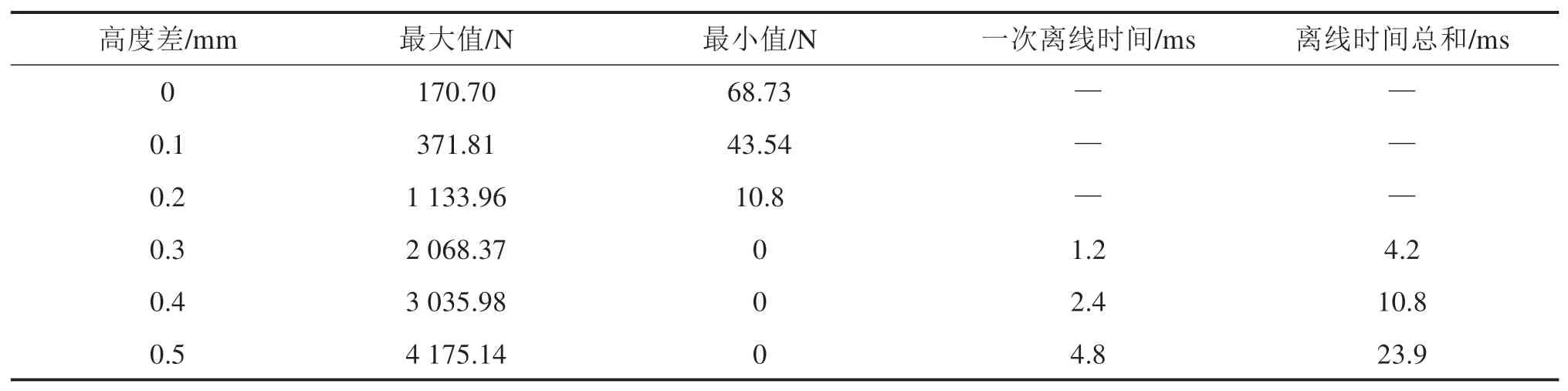
表4 不同接头高度差下的动态接触力及离线时间统计Table 4 Statistics of dynamic contact force and off-line time under different joint height differences

3.3 运行速度的影响

为探究不同运行速度对靴轨系统动态特性的影响，取不平顺接头前后各2 m区段，接头高度差取0.2 mm，受流器静态接触压力为120 N，受流器加载速度分别为80，100，120和140 km/h，进行靴轨耦合系统动力学仿真，结果如图14所示。对不同运行速度下的靴轨动态接触力及离线时间作统计性描述，统计结果如表5所示。

由图14可知，当不平顺接头高度差一定时，不同速度下靴轨系统的动态响应不同。受流器通过不平顺接头时受到的冲击随速度的增加而增大，促使靴轨接触面机械磨耗增加；仿真区段内动态接触力波动范围随车速增加而增大。

由表5、图14可知，靴轨动态接触力最大值及波动范围随车速的增加而增大；在120 km/h以下，靴轨动态接触力最小值均大于0 N，未发生离线情况；在车速达到140 km/h时，靴轨出现0.1 ms的短暂离线，离线时间较短。因此，不平顺接头高度差在0.2 mm以内时，能够满足地铁车辆最高运行速度120 km/h的运营需求。

表5 不同运行速度下的靴轨动态接触力和离线时间统计Table 5 Statistics of dynamic contact force and off-line time of shoe rail under different running speeds

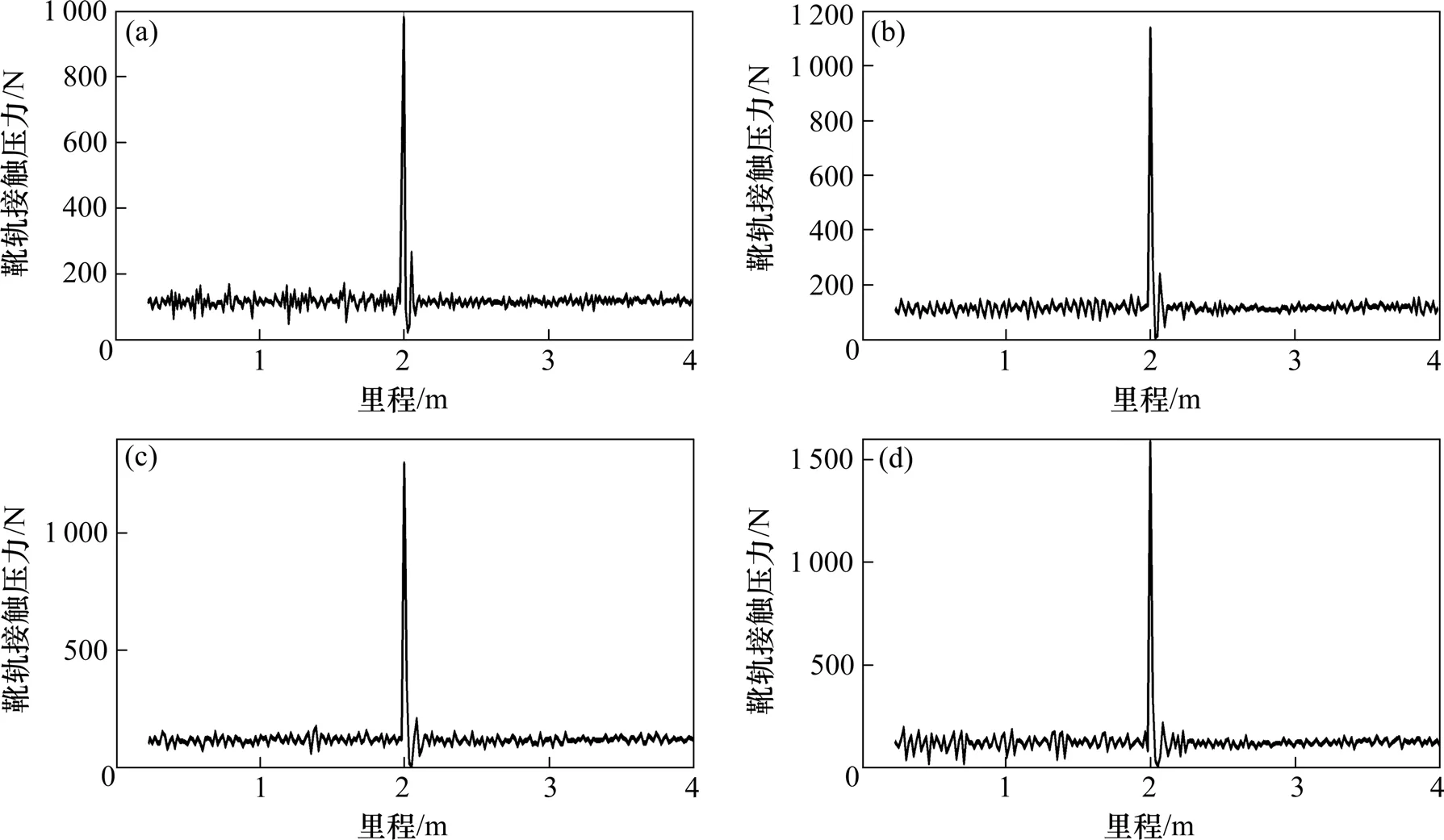
图14 不同速度下动态接触力Fig.14 Dynamic contact force at different speeds

3.4 不平顺接头的安全阈值分析

上述分析结果表明，在中间接头不平顺激扰下靴轨相互作用会加剧，从而影响靴轨动态受流质量。接头高度差作为中间接头不平顺的重要参数，现通过动态接触力及离线指标对靴轨动态受流质量作进一步分析，得出中间接头不平顺的安全阈值。不同接头高度差与接触力指标、离线时间指标的关系如图15所示。

图15 不平顺接头高度差与各指标关系Fig.15 Relationship between height difference of irregularity joint and each index

从不平顺接头高度差与动态接触力指标的关系可知，靴轨间的动力作用随不平顺接头高度差的增加明显加剧。在0～0.1 mm范围内，靴轨动态接触力最值变化较小；当接头高度差超过0.1 mm时，靴轨动态接触力最大值呈近似线性增加，最小值逐渐下降为0 N；当接头高度差从0.1 mm增大到0.5 mm时，靴轨动态接触力最大值从371.81 N增大到4 175.14 N，增幅为1 023%。

从不平顺接头高度差与离线指标的关系可知，靴轨离线时间随接头高度差增加而增加。在0～0.2 mm范围内，未发生靴轨离线；当接头高度差超过0.2 mm时，离线时间呈近似线性增加；当接头高度差从0.3 mm增大到0.5 mm时，一次离线时间从1.2 ms增大到4.8 ms，增幅为300%，通过不平顺接头的离线时间总和从4.2 ms增大到23.9 ms，增幅为469%。

综合分析，从靴轨动态接触力及离线指标统计结果考虑，建议第三轨中间接头不平顺高度差应控制在0.2 mm内，以减少靴轨冲击和降低离线率。

4 结论

1)靴轨动态接触力与弓网典型接触力不同，靴轨动态接触力呈现在非硬点区域波动平稳，在硬点区域局部高冲击的变化规律。

2)造成靴轨冲击的硬点来源为第三轨中间接头的不平顺。

3)利用靴轨动态仿真再现了局部不平顺导致接触力的局部脉冲峰。

4)靴轨冲击及离线时间随不平顺接头高度差、运行速度的增加而增加。

5)从动态接触力最值和靴轨离线时间考虑，第三轨中间接头不平顺高度差应控制在0.2 mm内。

后续工作可从滑靴磨耗与接触力的关系、电弧烧蚀与离线时间的关系以及受流器结构可靠性角度对接头不平顺阈值作进一步研究。