基于对照经验公式的构件本构模型离线更新混合试验方法

郭玉荣，刘兆民

(1.湖南大学 土木工程学院，湖南 长沙410082；2.建筑安全与节能教育部重点实验室，湖南 长沙410082)

混合试验作为研究结构抗震性能的重要方法之一，是将整体结构划分为物理子结构和数值子结构，其中物理子结构是在实验室中进行真实试验的复杂非线性构件，而数值子结构则通过有限元软件完成模拟试验[1−3]。在混合试验中，由于各类因素限制，只能对若干而非所有关键构件进行试验研究，造成了数值子结构中因构件的恢复力模型参数设置有误，而使混合试验最终结果不能真实地反应结构的抗震性能。模型更新的混合试验是在混合试验的基础上，利用物理子结构的试验数据识别的恢复力模型参数，将数值子结构中的参数进行更新修正，进而提升混合试验的精度[4]。模型更新的混合试验根据更新的时间可以分为在线模型更新和离线模型更新。在线模型更新混合试验是根据物理试验获得的数据，在线修正数值子结构中的数学模型[5]，但该方法对于待修正构件的数学模型的选取、参数识别的算法及识别精度、试验的精度等要求较高，导致在混合试验中有所局限性。相较于在线模型更新，离线模型更新虽当恢复力模型不能很好描述试验子结构特征或试验参数识别精度较低时，效果不如在线更新，但因是在获取试验子结构的试验数据后对其进行批处理，使其模型及识别算法选取包容性强，精度提升空间高，且试验数据的重复利用率较高[6]。当前的模型更新混合试验对于更新参数选择的研究主要分为3个层面：构件本构模型更新[7−8]、截面本构模型更新[9]及材料本构模型更新[10−11]。目前的构件本构模型更新混合试验，要求数值子结构与试验子结构完全相同，即要求两者有相同的截面尺寸、截面形状、轴压比、配筋率等构件参数。显然，对于复杂结构比如钢筋混凝土框架，往往存在多个参数不同的相似构件，取一个构件进行试验的模型更新混合试验方法对于提升试验精度有限。如果要提升混合试验的精度，一种方法是增加物理子结构的数量，但是它往往受限于试验场地及试验加载设备等因素。本文则从另一个角度，在有限的试验子结构数量和规模的条件下，研究如何充分利用试验数据获取的信息，对结构中构件参数不同的同类相似构件进行模型参数更新。一般地，构件本构模型基本上能描述其本构特征，但是按模型参数经验公式计算的参数往往存在误差，因此模型更新混合试验通过对试验子结构实测数据进行参数识别来校正经验公式计算的模型参数。由于同类相似构件往往具有相同的本构特征，把参数识别获取的校正系数应用于同类相似构件，则可以进一步提高混合试验的精度。因此，本文以各构件恢复力模型参数经验公式计算结果为初始值，物理子结构恢复力模型参数识别结果为识别值，将初始值与识别值进行对照计算从而获取一组恢复力模型参数修正系数，用以修正数值子结构中构件参数不同的相似相关构件经验公式计算的模型参数，将其称之为对照经验公式模型更新修正方法。首先介绍对照经验公式修正的基本原理，并选择IMK模型作为钢筋混凝土构件本构模型，然后基于离线模型更新以1榀采用截面配筋率不同的2层2跨弹性钢筋混凝土框架为例验证本文提出方法的可行性，最后利用OpenSees有限元软件完成1榀5层3跨钢筋混凝土弹塑性框架离线模型更新数值仿真，重复利用离线模型更新数据对1榀3层2跨框架进行模型更新，通过与传统构件本构模型更新混合试验仿真结果对比，表明基于对照经验公式的构件本构离线模型混合试验具有良好的性能，并可应用于离线模型更新中的数据重复利用。

1 对照经验公式修正基本原理

基于对照经验公式的构件本构离线模型更新混合试验方法的主要思想是：钢筋混凝土框架中柱构件因构件参数如轴压比、配筋率、截面尺寸等异同，导致构件的恢复力模型参数各不相同。在整体结构中，所有柱构件都可以利用混凝土规范或经验公式计算获得一组非精确恢复力模型参数，将通过这种方式计算获得的结果称为对照组。同时，对于混合试验中的物理子结构，通过参数识别的方式可以获取柱构件的真实恢复力模型参数。将物理子结构的参数识别结果同该构件的对照组计算结果进行正向对比，以正向对比误差作为修正基准，反向修正待更新数值子结构中柱构件对照组恢复力模型参数，从而完成数值子结构中构件参数不同柱构件的修正更新，以此来达到提高混合试验的精度的目的。基于对照经验公式的离线模型更新混合试验方法流程如图1所示。

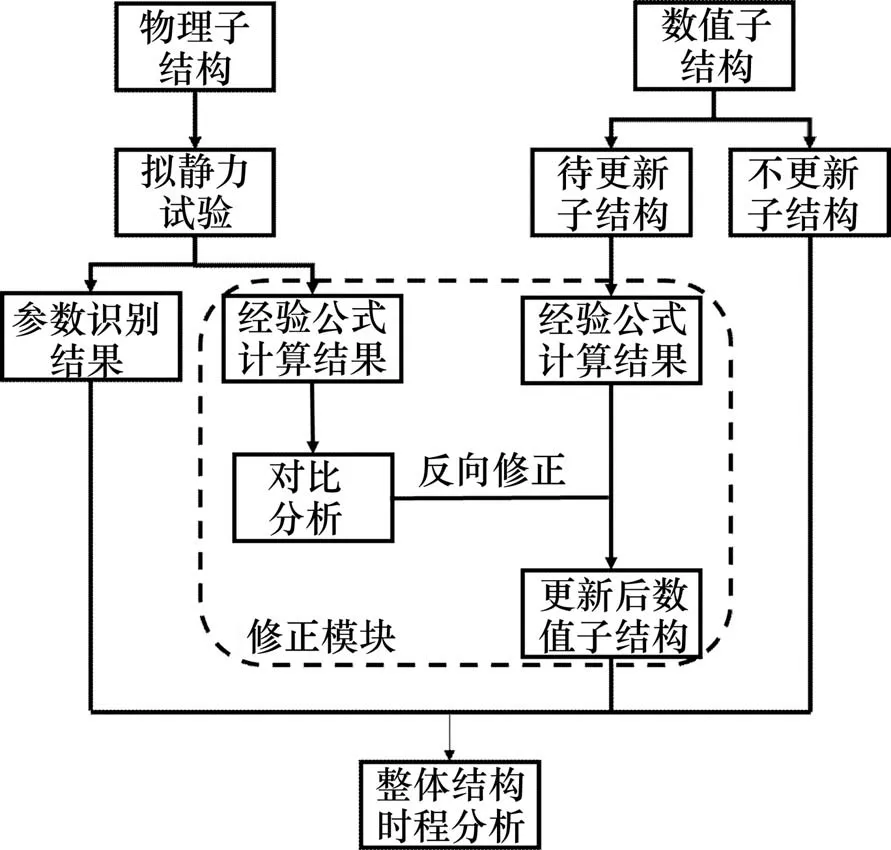
图1 基于对照经验公式的离线模型更新混合试验流程图Fig.1 Flowchart of hybrid simulation for off-line model update based on comparative empirical formula

该方法与传统模型更新混合试验不同的地方是增加了对照经验公式修正模块，用以修正构件参数不同的数值子结构构件的恢复力模型参数。对照经验公式修正模块主要包含3个子模块：对照组建立模块、正向对比分析模块、反向修正更新模块。在本文中对照组的含义是作为建立对比和修正基准的一个恢复力模型参数经验公式计算结果集合。对照组的建立需要选择合适的恢复力模型参数经验公式，这将对混合试验的精度造成影响。正向对比分析子模块是由物理子结构试验的恢复力模型参数识别结果及该构件对照组恢复力模型参数组成。对于混合试验，物理子结构试验恢复力模型参数仅能通过参数识别获取一组样本，故无法进行线性或非线性的回归分析，因此本文选用正比例线性修正方法，如式(1)所示，计算得到参数修正系数。根据正向对比分析结果，对待更新数值子结构构件的对照组恢复力模型参数进行线性修正更新。通过上述修正模块的修正计算即可完成对构件参数不同的数值子结构构件更新。

式中：xi为通过经验公式计算的构件各个恢复力模型参数初始值；yi为物理子结构参数识别获得的恢复力模型参数真实值；ki为各恢复力模型参数的修正系数。

在线模型更新的混合试验采用拟动力试验的方式，试验流程较为复杂，且受本文修正更新算法及经验公式选择的不确定性影响，可能会使混合试验无法准确的反映结构的抗震性能。而离线模型更新混合试验对数据进行批量后处理，使经验公式及修正算法具有一定选择空间，且试验流程简单，便于操作。因此本文采用离线模型更新验证对照经验公式修正的可行性。

2 IMK恢复力模型

本文修正方法需对柱构件恢复力模型参数按照经验公式进行计算并建立对照组，因此选用IMK模型作为混凝土框架中待更新数值子结构柱构件的恢复力模型，IMK模型由IBARRA等[12−13]提出，该模型将恢复力骨架曲线简化为三线性，即弹性段、强化段及软化段，它能够模拟混凝土梁柱的强度、刚度退化等现象，如图2所示。其骨架曲线形状由5个参数EIy，θcap,pl，θpc，My和Mc/My确定。HASELTON等[14]通过大量钢筋混凝土柱的试验数据建立了IMK恢复力模型中骨架曲线参数的经验公式，当钢筋混凝土构件为弯曲破坏时，计算公式如式(2)～(10)所示。

图2 IMK模型骨架曲线Fig.2 Skeleton curve of Ibarra-Medina-Krawinkler model

式中：EIy为割线模量；θcap,pl为塑性转角；θpc为峰值点后软化段塑性转角；My为屈服弯矩值；Mc/My为峰值弯矩与屈服弯矩的比值；φy为屈服曲率；ky，A和B为构件基本信息计算出的参数；P/Ag f′c，v为轴压比；b和d分别为柱横截面的宽和高；δ′=d′/d，d′为受压钢筋中心与受压区边缘之间的距离；n=Es/Ec，Es和Ec分别为钢筋和混凝土的弹性模量；asl为纵向钢筋滑移系数(考虑取1，不考虑取0)；f′c为混凝土圆柱体抗压强度；fy为受拉钢筋屈服强度，MPa；ρsh为柱塑性铰区横向钢筋面积比；ρ为纵向钢筋配筋率；ρ′为受压钢筋配筋率；ρv为抗剪钢筋的配筋率。

3 弹性RC框架构件本构模型更新数值仿真

3.1 OpenSees整体框架建模

为验证基于对照经验公式的构件本构离线模型更新混合试验方法的可行性，本节以中柱配筋率与边柱配筋率不同的1榀2层2跨弹性钢筋混凝土框架为例，通过OpenSees有限元软件进行离线模型更新混合试验，钢筋混凝土框架结构模型如图3所示。

框架建模采用二维杆系模型，各节点包含2个平动和1个转动共3个自由度。框架层高3.0 m，跨度为6.0 m，梁柱截面尺寸分别为400 mm×400 mm，200 mm×500 mm。框架梁柱构件采用IMK模型进行建模，第1刚度段参数设置为合理范围使构件始终处于弹性阶段。因需采用对照经验公式的更新修正方法，故对照组参数取为梁柱单元的弹性模量，对照经验公式取为框架柱换算弹性模量，计算公式如式(11)所示：

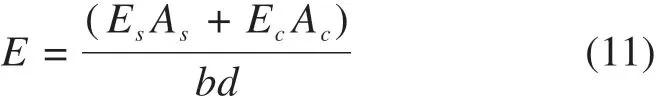
式中：As和Ac分别为钢筋和混凝土的截面面积。

框架结构计算模型选用C35混凝土及HRB335钢筋，2种材料的弹性模量如表1所示，其中初始值为经验值，真实值为假定试验结果。为设计不同配筋率的模型更新混合试验，试验采用不同配筋形式的边柱和中柱，边柱配筋率为0.29%，中柱配筋率为0.43%。地震时程分析输入选为EI Centro波，持续时间为10 s。

表1 钢筋和混凝土弹性模量Table 1 Elastic modulus of concrete and rebar MPa

3.2 离线模型更新混合试验数值仿真

混合试验取底层边柱为物理试验子结构，进行拟静力试验，对试验结果进行参数识别，并将公式(11)计算所得的弹性参数值作为对照组，对数值子结构中中柱刚度进行线性修正，柱弹性模量预测值如表2所示。

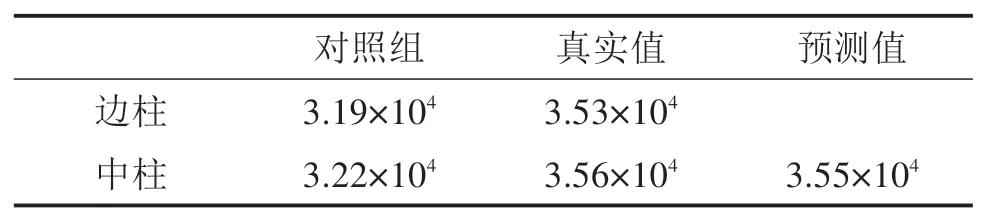
表2 柱弹性模量预测值Table 2 Predicted column elastic modulus MPa

弹性钢筋混凝土框架地震时程分析采用以下4种工况：1)初始值；2)真实值；3)传统构件本构离线模型更新混合试验，简称为传统构件更新；4)基于对照经验公式的构件本构离线模型更新混合试验，称之为对照构件更新。框架时程分析结果如图4所示。

图4 弹性框架结构时程响应Fig.4 Time history responses of elastic frame structure

由表2可以看出对照经验公式修正方法对于中柱弹性模量的预测值与真实值相差不大，说明本文所提出的对照经验公式模型更新方法可以有效地预测构件参数不同的相关相似构件。分别计算初始值、传统模型更新混合试验、本文试验方法的时程分析结果同真实值间的误差列于表3，误差参考标准取为底部剪力与顶点位移的RMSE值，计算公式如式(12)所示：

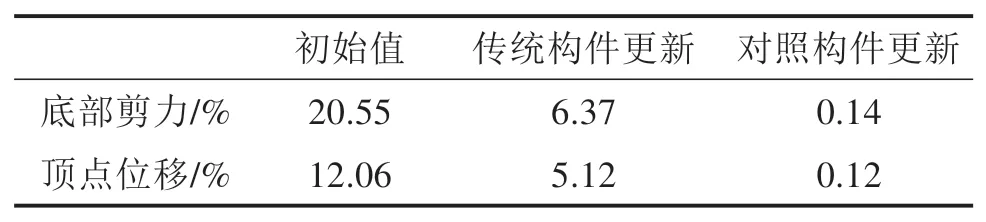
表3 不同工况下RMSE值Table 3 RMSE under different working conditions

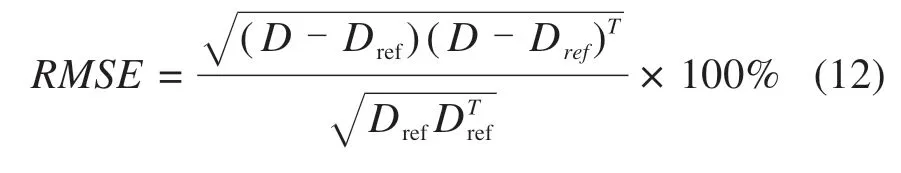
式中：Dref，D分别为真实值和各工况仿真结果的向量，T为向量转置。

由各个工况底部剪力及顶点位移RMSE值可以明显的看出，基于对照经验公式的构件本构模型更新混合试验方法均方根误差小于传统模型更新混合试验方法，相较而言本文试验方法可以从构件本构层面显著提升混合试验精度。

不同于传统构件本构模型更新混合试验仅能对构件恢复力模型参数相同的构件进行更新，这种新的模型更新方法可以对不同恢复力模型参数的相似构件进行更新。对于复杂结构的模型更新混合试验，本文方法可以扩大更新的构件数量及范围，进而提升混合试验的精度。

4 弹塑性RC框架构件本构离线模型更新与应用

4.1 OpenSees整体框架建模

为检验基于对照经验公式的构件本构模型更新混合试验方法的有效性及离线模型更新数据重复利用的可靠性，本节通过OpenSees有限元软件进行1榀5层3跨钢筋混凝土弹塑性框架(框架A)离线模型更新混合试验数值仿真，并重复利用物理子结构试验数据完成1榀3层2跨钢筋混凝土框架(框架B)离线模型更新数值仿真。

2个框架均采用相同的构件参数和尺寸参数，框架层高3.0 m，跨度为6.0 m，梁柱截面分别为400 mm×400 mm，200 mm×500 mm。框架梁柱构件均采用基于力的非线性梁柱单元，并考虑轴力与弯矩的耦合，每个单元采用3个积分点，截面为纤维截面，混凝土纤维及钢筋纤维分别选用Con‐crete01和Steel02本构模型，两者本构模型参数见表4。地震时程分析输入选为EI Centro波，持续时间为10 s。

表4 材料本构模型参数Table 4 Material parameters of constitutive model

4.2 物理子结构拟静力试验及参数识别

取框架A底层边柱作为物理子结构，物理子结构模型建立采用4.1节相同的构件及截面参数。对子结构构件进行足尺拟静力数值仿真试验，构件底端约束，顶端有限转动，柱顶施加恒定轴力P=247.6 kN。以构件顶端位移控制加载，所加水平位移依次为5，10，15，20，25，30，40，45，55 mm。

物理子结构拟静力试验数值仿真结果如图5(a)所示，其中真实值及初始值分别对应表4中材料的不同数值仿真结果。提取构件拟静力试验结果真实值的骨架曲线，利用Matlab编程的差分进化算法[15]对骨架曲线进行参数识别。拟静力试验构件未进入第3刚度段及倒塌阶段，故IMK模型参数识别仅识别弹性段和强化段。根据参数识别结果，对物理子结构IMK恢复力模型参数进行计算。利用OpenSees完成物理子结构的IMK模型建模，并施加以相同加载方式，IMK模型拟静力计算结果如图5(b)所示，可见使用参数识别结果的IMK恢复力模型可以较好地反应构件的滞回性能。

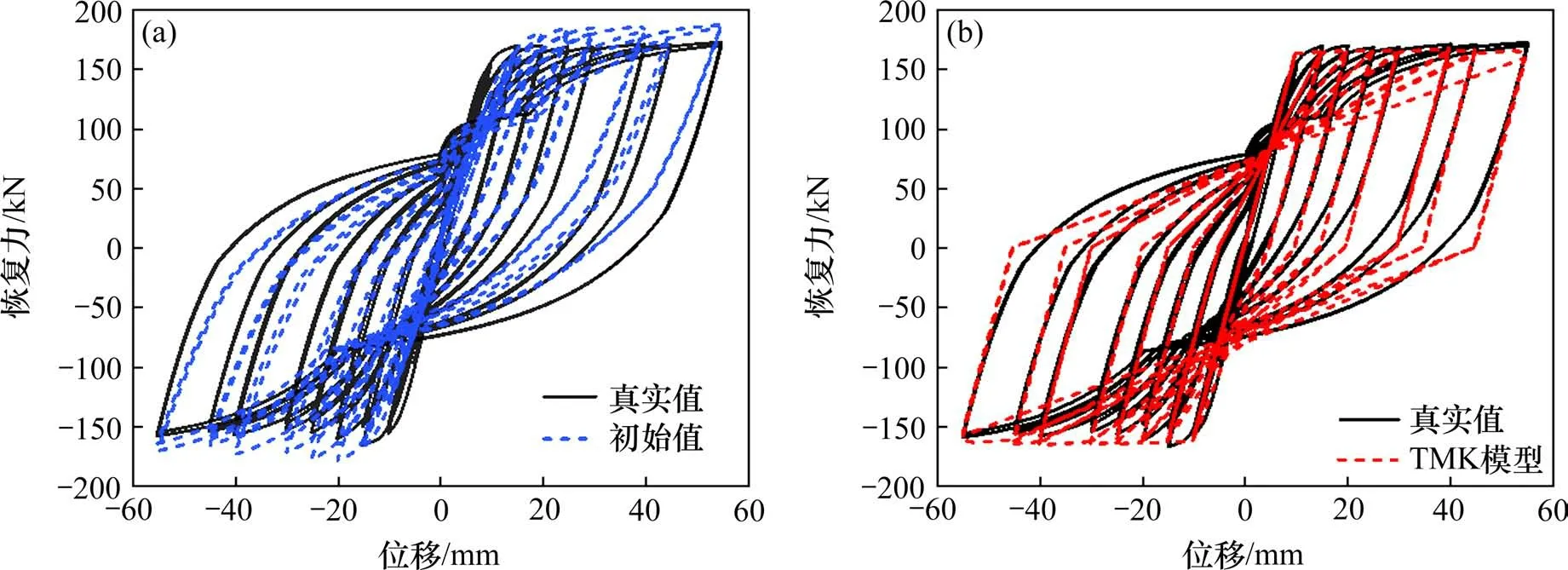
图5 物理子结构拟静力结果及参数识别Fig.5 Pseudo-static results and parameters identification of physical substructure

4.3 离线模型更新混合试验数值仿真

因框架结构中柱构件的轴压比各不相同，即恢复力模型参数不同，所以采用对照经验公式的构件本构离线模型更新混合试验对钢筋混凝土框架进行地震动作用下的时程分析数值仿真。

构件本构模型更新混合试验的最终目标是对所有数值子结构中的同类构件进行修正，但本文对照经验公式修正算法为线性相关修正，且恢复力模型参数数量较多，修正结果存在不确定性，故对于对照经验公式的构件本构离线模型更新工况中，仅对底层中柱的恢复力模型参数进行预测更新修正。

根据第2节所介绍的IMK恢复力模型参数经验公式，计算物理子结构的对照组子集，与参数识别获得的恢复力模型参数组成正向对比分析子模块。根据柱构件的轴压比反向线性相关修正待更新构件对照组恢复力模型参数，如表5所示，未识别修正的数据按照经验公式进行选取。对几种工况进行地震动时程分析。分析结果如图6所示。

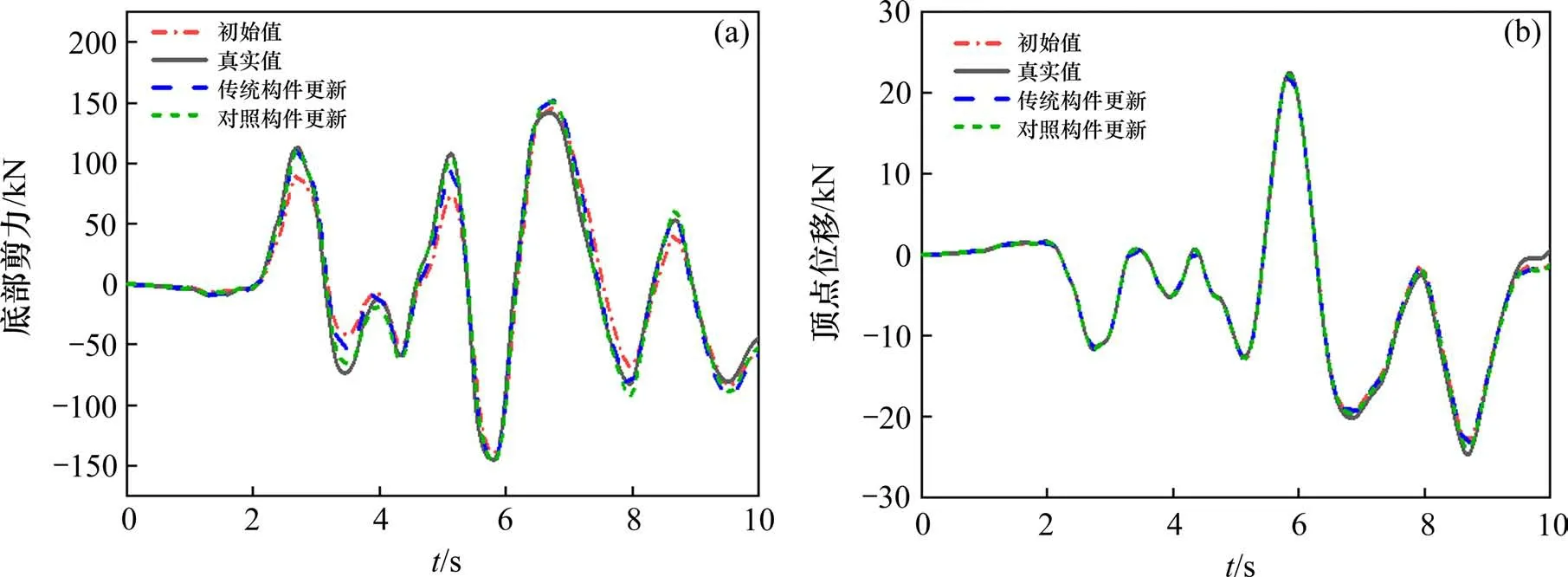
图6 框架A结构时程响应Fig.6 Frame A structure time history response

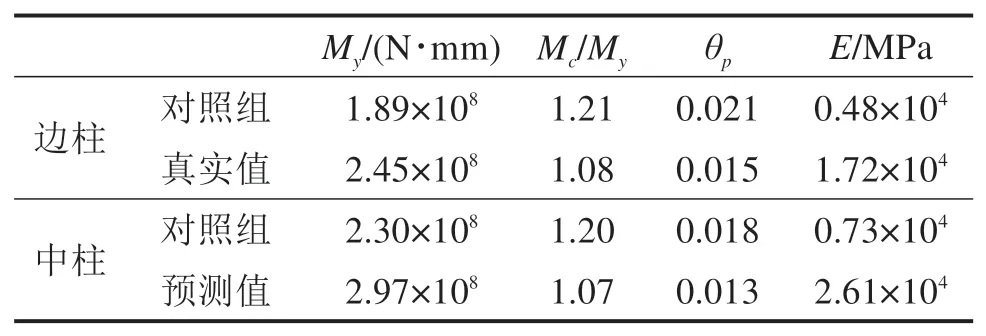
表5 框架A中IMK恢复力模型参数预测Table 5 IMK hysteretic model parameter prediction of frame A

对比几种工况下的RMSE值，如表6所示。可以明显看出，对照经验公式修正可以提升模型更新混合试验的精度。但由于受到修正算法及恢复力模型经验公式选择的限制，修正精度还有待提高。

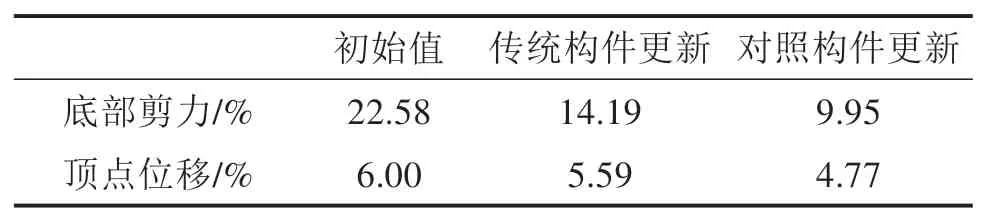
表6 框架A各工况RMSE值Table 6 Frame A RMSE for each working condition

4.4 离线模型更新数据重复利用

根据4.3节物理子结构对照组正向对比修正子模块，对框架B进行底层柱离线模型更新混合试验，以此来完成离线模型更新数据的重复利用。时程分析参数及工况分类与框架A相同。对各构件恢复力模型参数的修正如表7所示。

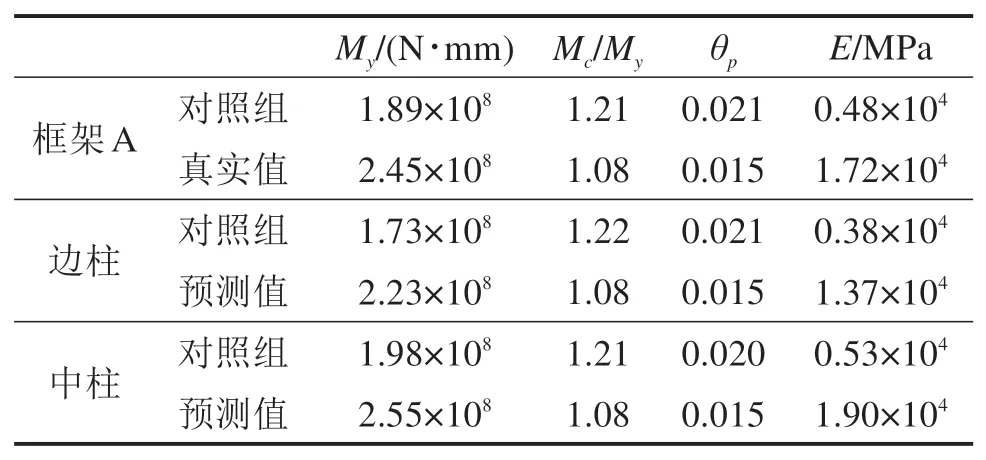
表7 框架B中IMK恢复力模型参数预测Table 7 IMK hysteretic model parameter prediction of frame B

对比几种工况下的RMSE值，如表8所示。可以看出对于构件及截面参数相同的不同结构，离线模型更新的试验数据可以通过本文提出的对照经验公式方法进行重复利用，并提高混合试验的精度。

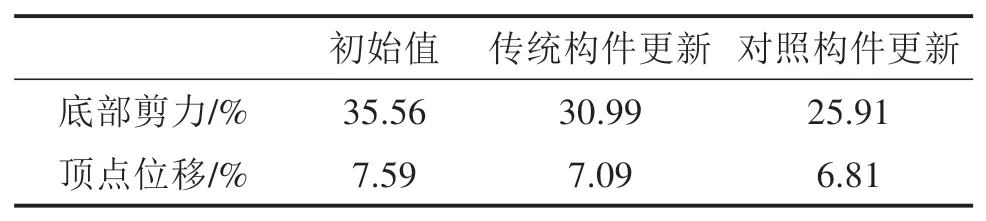
表8 框架B各工况RMSE值Table 8 Frame B RMSE for each working condition

5 结论

1)提出了基于对照经验公式的构件本构离线模型更新混合试验方法，通过弹性及弹塑性钢筋混凝土框架离线模型更新混合试验算例，证明该方法可以提高模型更新混合试验的精度。

2)修正更新方法的精度受恢复力模型选择及修正算法等因素影响。使用更精确的恢复力模型和更可靠的修正算法可以进一步提升该方法的修正精度。

3)离线模型更新混合试验流程精简，本文所提出的对照经验公式修正方法亦可应用于离线模型更新数据的重复利用。