地质雷达信号定量识别用小波基选取的正演及模型试验研究

周智辉，凌同华，杨志刚，吴维祥，张亮，何文超

(1.长沙理工大学 土木工程学院，湖南 长沙410114；2.中铁南方投资集团有限公司，广东 深圳518000；3.湖南城市学院 土木工程学院，湖南 益阳413000)

随着人民群众对交通运输需求的日益增大，我国高速公路、铁路等建设项目迎来了高速发展期，高速公路、铁路的建设里程和规模不断增大，其中隧道工程的数量也日益增多[1]。在隧道施工中，由于现场地质地形条件、设计及施工工艺的影响，衬砌结构背后极可能出现空洞、衬砌厚度不足或回填不密实等质量缺陷[2−4]。空洞的存在将对隧道的运营产生安全隐患[5−6]。准确、及时地发现和处理空洞问题是保证隧道安全施工和确保隧道未来正常运营的关键。地质雷达探测法具有高效、简易、准确度高等优点，常被运用于隧道衬砌结构质量检测与分析中。巴特尔[7]详细阐述了隧道衬砌结构中常见的脱空、衬砌混凝土厚度不足等质量缺陷的成因及其典型的雷达图像特征，并采用地质雷达技术对某铁路隧道衬砌缺陷分布进行分析和研究；白运等[8]以某高速公路隧道段混凝土衬砌地质雷达检测为例，研究了检测过程中测线布置、测试仪器参数选择等重要问题，通过实际检测与数据分析，得到了衬砌背后空洞与不密实带的大致位置；穆伟[9]对衬砌背后空洞缺陷的几种地质雷达波形图进行解译与分析，归纳并总结了空洞缺陷的典型雷达波特征和规律，并对空洞产生的原因进行了阐述。采用地质雷达法能有效检测出衬砌结构背后空洞缺陷问题，但目前的研究基本上都是停留在对质量缺陷问题的定性识别上，没有涉及到目标体的精确量化识别问题[10−11]。缺陷目标体的量化识别涉及地质雷达信号奇异特征点的提取问题，小波分析是信号特征点提取的有效方法[12]。缺陷目标体量化识别的准确与否与小波分析所用的基函数密切相关。不同的小波基具有不同的时频局部化特性，在对非平稳信号进行奇异性分析时，存在最优小波基的选取及其算法与实现问题。本文在小波分析基本原理及信号特征点识别理论基础上，在对比不同小波基函数对称性及对地质雷达信号重构精度等基本性质后，采用小波时-能密度法对空洞缺陷的埋深及垂直尺寸进行定量计算，并对适合于RIS型地质雷达信号奇异性分析的最优小波基进行选取，以提高对质量缺陷的识别精确度，从而为隧道衬砌结构质量缺陷整治和安全性控制提供准确参考。

1 小波分析及信号特征点识别理论

1.1 小波基本理论

在Hilbert空间中，如果函数ψ(x)∈L2(R)满足容许条件：

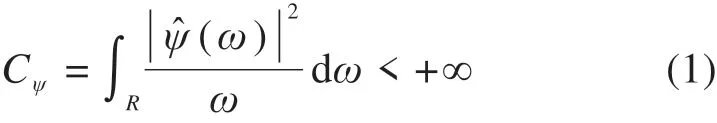
且 满 足 规 范 化 条 件|ψ|22=1，其 中ψ̂(ω)为ψ(x)的傅里叶变换，则称ψ(x)为母小波。母小波经移位和伸缩可产生的一组函数

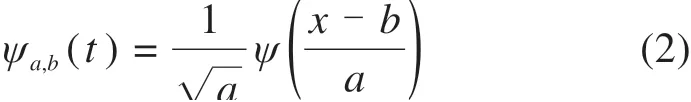
称为小波基函数(母函数)，其中，a为伸缩因子，b为平移因子，有a,b∈R，且a≠0。

设f(x)∈L2(R)，ψ(x)为母小波，定义公式

为关于基小波ψ的连续小波变换。其中，Xˉ表示X的共轭运算。连续小波变换将原来的一维信号变换成二维信号，以便于分析信号的时频特性。

1.2 小波变换时−能密度法

对于信号x1(t),x2(t)和小波函数ψ(t)，若x1(t)，x2(t)的小波变换分别为WTx1(a,b)和WTx2(a,b)，则有：

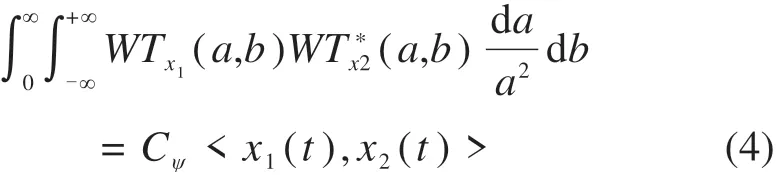
式中：

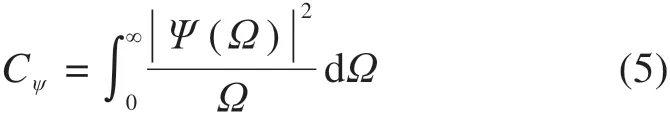
Ψ(Ω)为ψ(t)的傅氏变换。

式(4)即为小波变换的Parserval定理，该式可表示成如下简洁形式：

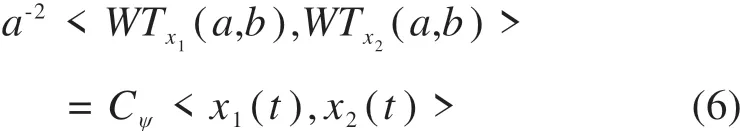
若令x1(t)=x2(t)=x(t)，根据式(4)，有：

此式表明，小波变换的幅平方在尺度−位移平面上的加权积分与被分析信号在时域上的总能量成正比，小波变换的幅平方可看成是信号能量时频分布的一种表示形式。在非平稳信号的处理中，受Heisenberg测不准原理的限制，在时−频相空间中某一点的瞬时能量密度是无法确定的。但在式(7)中，可以将|WTx(a,b)|2/Cψa2看作是尺度-位移平

从表1可看出，Db小波系具有非对称特征且对地质雷达信号的分解重构误差普遍较大。当小波函数不具备线性相位时，信号在分解过程中易产生频率混叠、相位失真等问题。因此，Db小波系不适合用于地质雷达信号分析。Bior4.4，Bior5.5和Bior6.8小波虽然具有线性相位，但对信号的重构误差较大，因此它们也不宜作为地质雷达信号分析用小波基。偶数阶消失距Bior系小波基中Bior2.4和Bior2.6双正交基对信号重构误差较小，并且两者重构误差相当，但Bior2.6小波基消失距更高，函数更光滑，因此，偶数阶消失距Bior系小波基中初步选择该小波函数进行地质雷达信号奇异性分析。同理，奇数阶消失距Bior系小波基中Bior3.7和Bior3.9双正交基对信号重构误差较小，且Bior3.9小波基消失距更高，函数更光滑，因此，奇数阶消失距双正交小波基中初步选取面上的能量密度，由此可将看作是以尺度a和位移b为中心的、尺度间隔为Δa，位移间隔为Δb的能量。根据能量密度的概念，式(7)可以改写为

式中：

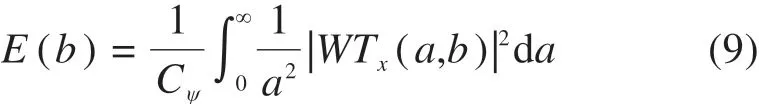
小波变换中的尺度a是一个与信号频率相关的参数。因此，式(9)表示信号所有频带的能量随位移b的分布情况，即时−能密度函数。

2 小波基函数初选

首先从小波函数的线性相位、对信号的分解重构误差大小等角度选择适合于地质雷达信号奇异性分析用较优小波基。小波分析的最重要应用是滤波，为了保证滤波不失真，小波函数应具有线性相位。信号的多尺度重构误差分析能直观反映小波基函数的重构效果及小波函数与被分析信号之间的适应性。分别比较已有的Db系、Bior系小波基的对称性及对实测RIS型地质雷达信号的重构效果，并对地质雷达信号奇异性分析用较优小波基进行初选。各小波基的分析对比结果见表1。

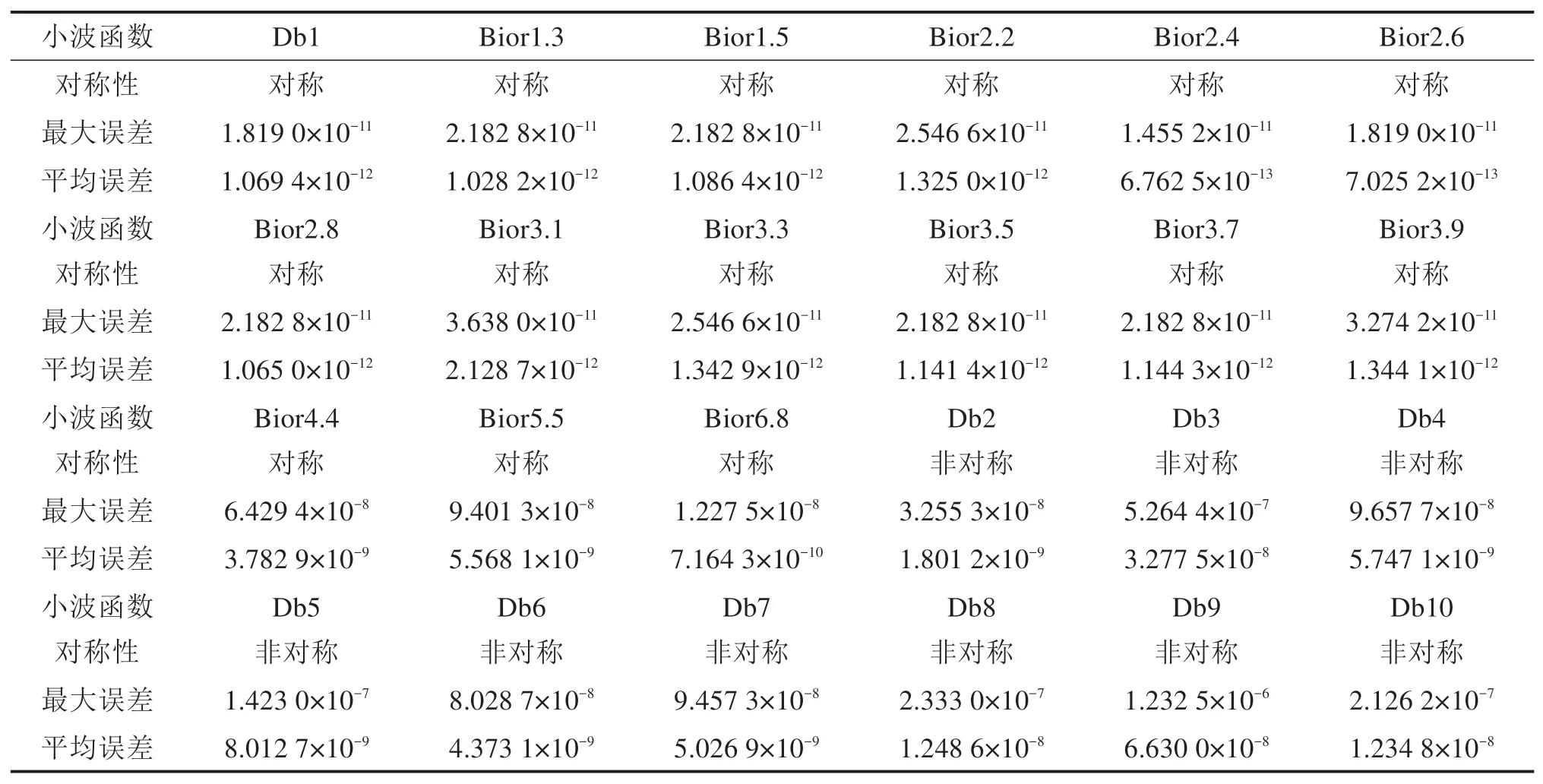
表1 各小波基对称性及重构误差比较Table 1 Comparison of symmetry and reconstruction error of each wavelet basis

Bior3.9函数作为地质雷达信号奇异性分析用基函数。

3 正演模拟信号奇异性分析

3.1 正演模拟试验

设计空洞地质雷达探测正演试验，基于初选的2种小波基函数，采用小波时-能密度法进行正演信号特征点识别及空洞尺寸量化分析，并对适用于RIS型地质雷达信号奇异性分析的最优小波基进行选取。空洞探测模型长2.00 m，高0.95 m，在模型上部存在一空洞缺陷，空洞长为0.20 m，高0.18 m，埋深0.17 m。运用GPRMAX软件对含空洞混凝土模型进行正演模拟检测，模拟时窗为12.076 ns，空间网格步长为Δx=Δy=0.005 m，天线步距为L=0.01 m，天线中心频率为1 600 MHz，参数设置详见表2。

表2 空洞正演模拟试验参数设置Table 2 Parameter setting of cavity forward simulation test

3.2 基于小波时−能密度法的信号奇异性分析

提取正演结果中反映空洞位置信息的单道信号，基于初选得到的Bior2.6和Bior3.9双正交小波基，采用小波时−能密度法对单道信号进行特征点提取与定量分析。

3.3.1 Bior2.6小波基识别结果

采用Bior2.6双正交基作为基函数，第97道信号的小波时-能密度分析结果如图所示，其中图1(a)表示直达波信号时−能密度分析结果，图1(b)表示空洞信号时−能密度计算结果。图中点1表示传播介质的表面反射波位置，点2，3分别表示空洞的上、下表面反射波位置，各点的起始时刻分别为0.720 1，1.688 0和3.022 0 ns，可计算出空洞埋深和垂直尺寸分别为18.22 cm和20.01 cm。与设计值相比，误差分别为1.22 cm和2.01 cm，相对误差分别为7.18%和11.17%，详见表3。

图1 基于Bior2.6小波基的时−能密度谱曲线Fig.1 Time-energy density spectrum curve based on Bior2.6 wavelet basis

3.3.2 Bior3.9小波基识别结果

选用Bior3.9双正交基对单道信号作小波时−能密度分析，结果如图2所示。各点的起始时刻分别为0.661 1，1.782 0和3.105 0 ns。可计算出空洞埋深和垂直尺寸分别为19.16 cm和19.85 cm。与设计值相比，误差分别为2.16 cm和1.85 cm，相对误差分别为12.71%和10.28%，详见表3。

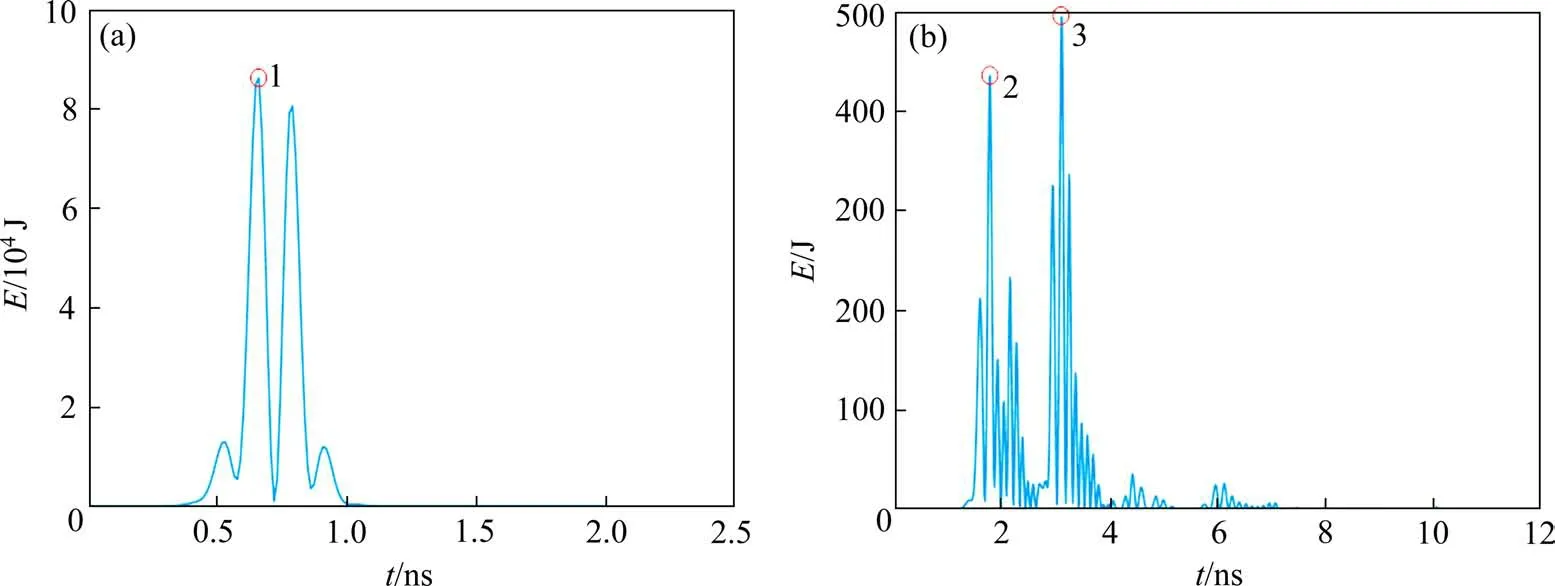
图2 基于Bior3.9小波基的时−能密度谱曲线Fig.2 Time-energy density spectrum curve based on Bior3.9 wavelet basis

假设以空洞埋深和内部垂直高度计算值的误差百分比之和作为评价指标，从表3可知，Bior2.6双正交基的计算误差较小，即相对于Bior3.9小波基，由Bior2.6计算得到的空洞埋深和内部垂直高度与设计值更接近，表明该小波基更适合用于正演地质雷达信号奇异性判别中。

表3 正演信号小波时−能密度法定量分析结果Table 3 Quantitative analysis results of forward signal by wavelet time-energy density method

4 实测地质雷达信号定量分析

4.1 试验设计

设计已知埋深和尺寸的空腔检测试验，空腔用于模拟隧道衬砌结构中的空洞缺陷，运用地质雷达对含空腔缺陷的试验模型进行检测，并采用小波时−能密度法对地质雷达图像的空洞反射信号进行定量分析，比较不同小波基函数在RIS型地质雷达信号定量识别中的准确度。

空洞尺寸为长×宽×高=25 cm×25 cm×20 cm(空洞内部实际高度为18.8 cm)，空洞至沙槽表面的垂直距离为19 cm，其中空洞顶部干沙的埋置高度为18 cm，沙槽上覆测试用木板厚1 cm。空洞探测试验的详细参数设置见表4，试验设计示意图、探测过程及实测地质雷达图像结果分别见图3和图4。

图3 空洞地质雷达探测试验Fig.3 GPR detection test for cavity

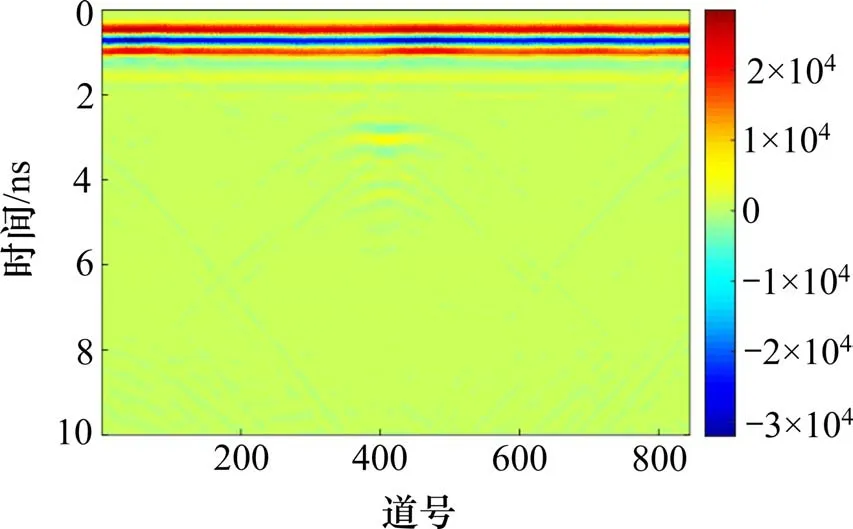
图4 地质雷达探测原始图像Fig.4 Original GPR detection image

表4 空洞探测试验详细参数设置Table 4 Detailed parameter setting of cavity detection test

4.2 地质雷达信号定量分析

基于初选的Bior2.6和Bior3.9双正交小波基，采用小波时-能密度法进行空洞反射信号特征点提取及空洞尺寸定量分析。定量分析用小波基分别为Bior2.6和Bior3.9小波基。提取含空洞位置信号的第410条单道信号，2种小波基计算得到的时能密度谱曲线分别见图5和图6。图中，t1为传播介质的表面反射波位置，t2和t3分别表示空洞上、下表面反射波时间位置。2种小波基计算得到的空洞位置值与实际值对比见表5。

表5 实测地质雷达图像定量分析结果Table 5 Quantitative analysis results of measured GPR image

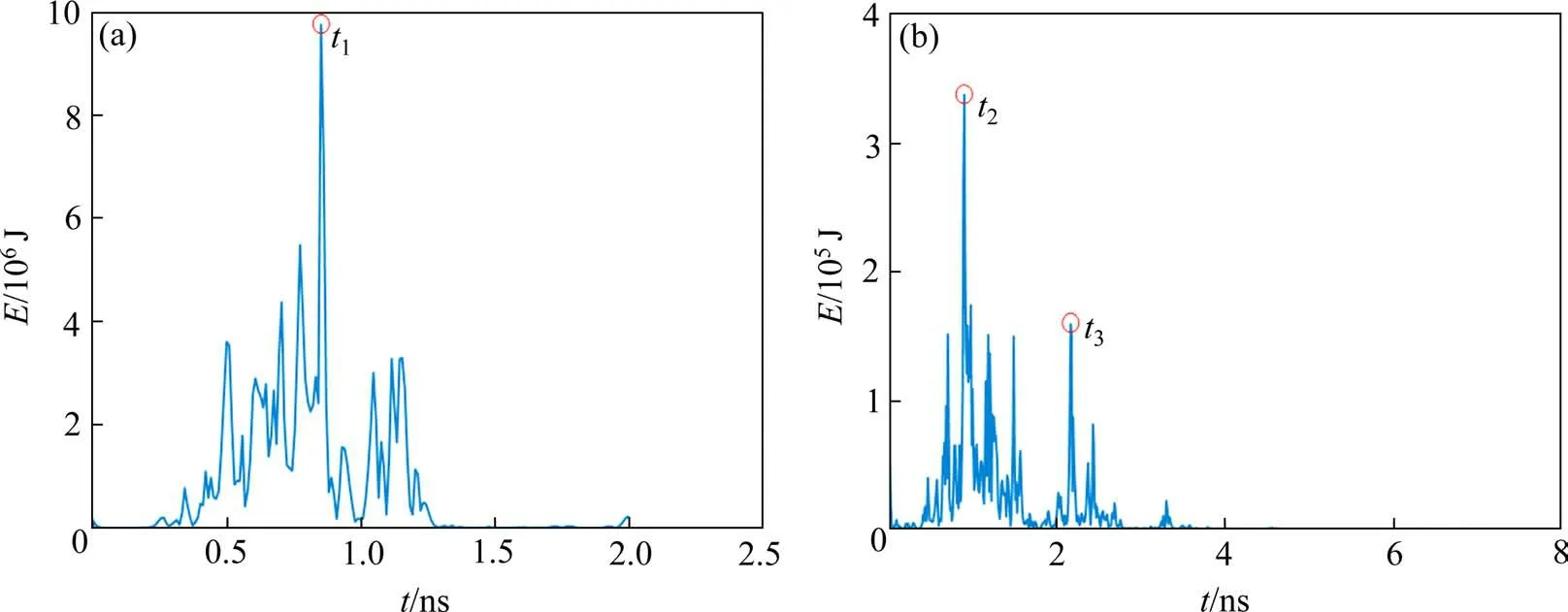
图5 基于Bior2.6小波基的时−能密度谱曲线Fig.5 Time-energy density spectrum curve based on Bior2.6 wavelet basis

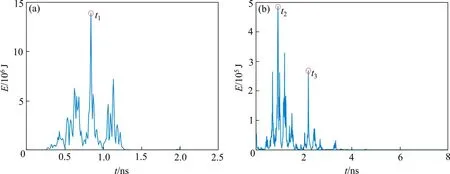
图6 基于Bior3.9小波基的时-能密度谱曲线Fig.6 Time-energy density spectrum curve based on Bior3.9 wavelet basis

由表4可知，小波时−能密度谱法计算出的空洞位置结果与实际值很接近，并且该方法对信号特征点的捕捉效果明显且易于判断。同样地，以空洞埋深和内部垂直高度计算值的误差百分比之和作为方法优劣评判指标，可知，Bior2.6小波基的计算误差和较小，由该小波基计算出的空洞埋深和内部垂直尺寸结果与实际值更为相近，说明该小波基在地质雷达信号奇异性检测方面具有较明显的优越性。

5 结论

1)由于Bior系小波具有线性相位且对实测地质雷达信号分解、重构误差小，因此选择该类小波用于地质雷达信号分析，其中偶数阶消失距Bior系小波-Bior2.6和奇数阶消失距Bior系小波-Bior3.9双正交基具有对雷达信号重构误差较小，且消失距更高，函数更光滑等优势，初步选取Bior2.6和Bior3.9小波函数作为地质雷达信号奇异性分析用基函数；

2)在正演及实测地质雷达信号奇异性分析中，相对于Bior3.9小波基，Bior2.6计算得到的空洞埋深和内部垂直高度与设计值更接近，该小波基的识别精确度较高，表明该小波基更适合用于地质雷达信号奇异性判别中。

3)小波时−能密度法对信号特征点的突出和放大作用非常明显，运用该方法能直接且精确地检测出地质雷达信号特征点所在位置，表明小波分析在非平稳信号处理中具有匹配性和适应性。

4)对衬砌质量缺陷进行精细化定量识别具有理论价值与实际意义，定量分析可为缺陷的危险等级划分及精确处治提供准确依据，从而在一定程度上维护工程的耐久性和安全性。