基于改进萤火虫算法的船舶装卸作业稳性研究

肖力旗，曹 民，张柳明

（1.上海理工大学光电信息与计算机工程学院，上海 200082；2.上海交通大学电子信息与电气工程学院，上海 200240）

0 引言

在经济全球化时代背景下，海洋运输在国际贸易、大型货物运输中拥有无可替代的地位，船舶是海洋运输最主要的交通工具，船舶稳性［1-2］是保障航运安全的重要指标。国际海事组织（International Maritime Organization，IMO）在第二代完整稳性衡准中确定了5 种失效模型［1］，以此规范不同状态船舶的稳性问题。在码头装卸作业工况下，船舶稳性易受诸多不确定因素影响［3-4］，研究该工况下的船舶稳性对码头作业安全具有重要意义。

针对船舶稳性的研究主要集中在船舶耐波性，研究方向主要包括两个部分：①在时域上研究特定波浪对船舶运动状态影响［5］；②基于统计思想，利用谱分析理论分析船舶在不规则波中的频域响应。Zhang 等［6-7］研究了规则和非规则波中参数横摇的数学模型，分析了稳性高度对船舶稳性的影响；朱军等［8］用摇晃耦合切片法分析横摇运动规律；Chakrabarti［9］对非线性横摇阻尼影响进行评估，结合实验提出在改进的经验公式；Yin 等［10］提出基于自适应滑动数据窗的船舶横摇预报方案，实现船舶横摇动态在线预测，这些研究为船舶横摇和稳性分析提供了研究基础。然而在港口风浪较小情况下，系泊装卸作业工况下船舶失稳主要受重物激励和重心变化影响，利用谱分析理论分析船舶在该工况下的稳性并不适用。

近年来，智能控制算法发展迅猛，算法不断优化，逐渐深入到各工业领域。Wu 等［11］利用模糊算法研究了船舶失稳各因素影响情况，但研究对象仍为航行中的船舶，利用智能控制算法研究装卸作业的船舶稳性较少。

针对系泊船舶装卸作业特殊的工况及稳性监测实时性问题，本研究通过分析横摇周期与初稳性高的关系，利用改进的萤火虫算法优化船舶横摇运动方程模型，预测船舶横摇运动状态，计算出船舶初稳性高，从而分析系泊船舶稳性。采用仿真实例验证了该方法的可行性和有效性。

1 模型理论依据

1.1 小倾角稳性

小倾角稳性也称初稳性，一般情况下小倾角指倾斜角小于10°～15°［12］。在正常气象状况下，港区船舶属于小倾角稳性问题，通常用初稳性高来描述该状态下的船舶稳性。2008 年IMO 船舶稳性规则中规定船舶初稳性高不应低于0.15m［13］。船舶在静水中的初稳性高与横摇周期存在如下关系［14］：

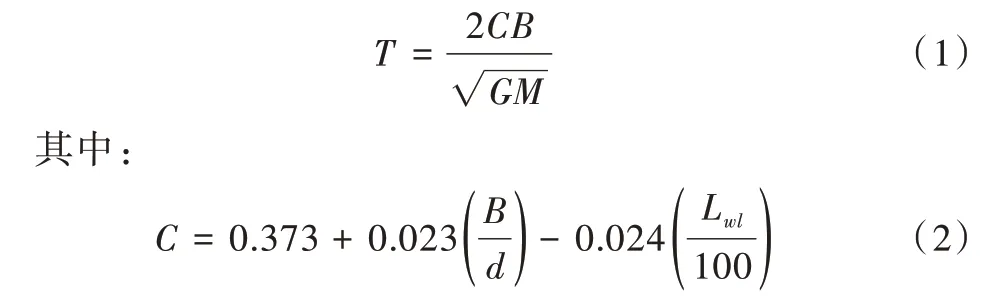
式中，GM为初稳性高，T为横摇周期，B为型宽，d为平均吃水，Lwl为设计水线长。

1.2 船舶横摇运动方程

对于船舶的横摇运动，若不考虑风浪流等外界干扰，船舶的横摇运动力矩方程［15］为：

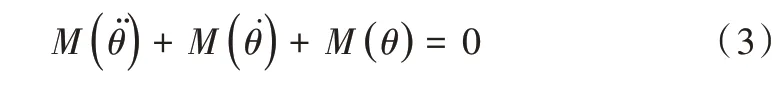
其中，M()是惯性力矩，与角加速度相关，M()是阻尼力矩，与角速度相关，M()是回复力矩，由倾斜角度决定。对于线性阻尼，船舶横摇运动方程可写为［16-17］：

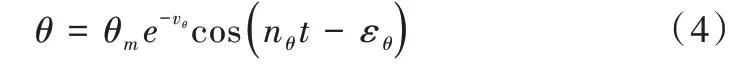
其 中，θm是横摇最大倾角，vθ是横摇衰减系数，vθ=μθnθ，μθ为无因次衰减系数，nθ为船舶横摇固有频率，εθ是其相位角。

船舶在静水中受到外界一定倾角的作用下，其横摇做衰减振荡。由于在船舶装载过程中很难保持船舶左右两侧的平衡，因此在船舶横摇幅度衰减到极小时可能会出现稳态倾角θ0。若考虑稳态倾角情况，则横摇公式可写为：

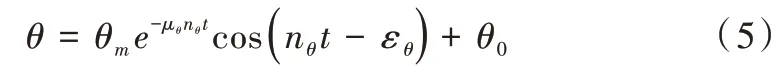
由于船舶装载作业是间断性的加装货物，本研究需要在尽可能短的时间内根据已检测到的船舶倾角信息，将其横摇周期及稳态倾角解算出来。式（5）中，已知一定长度的倾角和时间序列，而还有θm、μθ、nθ、θ0、εθ五个参数是未知的，对于5 个未知参数的非线性曲线拟合其计算量相当大，无法满足在一次装载间隔内计算出横摇周期需求，因此需要根据其他特征确定部分参数。

1.3 倾角序列前期处理

实际工作环境中，船舶在港口装载货物时，其工作环境风浪较小，但仍然不可忽略其影响。由于风浪噪声属于混沌系统，其干扰函数难以确定，通常使用多项式拟合方法使倾角信号更加平滑。

假设采集到的倾角序列为{θ1,θ2,θ3...θj}，按一定长度截取序列进行分段多项式拟合，利用来替代原信号的值。tj为采集到θj倾角值对应的时间，倾角信号采样频率T=tj+1-tj，ai为多项式系数。将ai以某一初值进行迭代，当达到最小时获得最佳多项式系数aj的值。采用梯度下降法来加快迭代速度。在多项式拟合过程中，为提高拟合速度、防止过拟合，选取的多项式阶数不应过高，截取的序列长度应与多项式阶数相关。

对于已经经过多项式拟合的数据，其波峰（波谷）处一阶导数为0。在一个激励作用下，横摇曲线是随时间衰减的曲线，横摇最大倾角即为第一次出现的波峰（波谷）倾角θmax。将出现横摇最大倾角的时间标定为0 时刻，有εθ=0（若第一个为波谷，则εθ=π/2）。将θmax、t=0 代入式中，可得θmax=θm+θ0。则式（5）可写为：

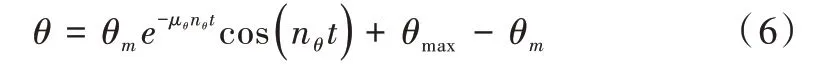
在该式中，存在θm、μθ、nθ三个未知参数，要得到横摇曲线参数的最优解，本研究使用萤火虫算法进行横摇参数求解。

2 改进萤火虫算法

2.1 标准萤火虫算法

萤火虫算法（Firefly Algorithm，FA）是一种基于自然启发的群智能优化算法，来源于萤火虫发光并相互吸引的行为［18］，其原则可简化为：

（1）每个萤火虫相互吸引无性别区分。

（2）相对亮度与距离平方成反比，当距离过大时无吸引力。

（3）亮度取决于是否接近目标函数的最佳优化。亮度越大，吸引力越大，小的萤火虫向亮度大的移动，移动速度与吸引力大小相关。

其中，萤火虫相对距离为笛卡尔距离。第i只萤火虫与第j只萤火虫的笛卡尔距离rij为：

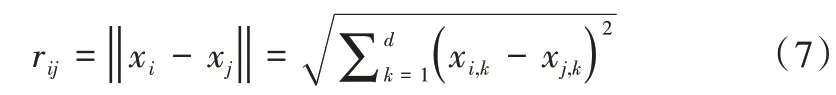
其中，xi为第i只萤火虫空间坐标，d为萤火虫所在空间维数。若第i只亮度高于第j只，则第i只萤火虫对第j只萤火虫的吸引力βj为：

其中，β0为最大吸引力，γ为光吸收强度系数。第j只萤火虫向第i只萤火虫移动时位置更新为［19］：

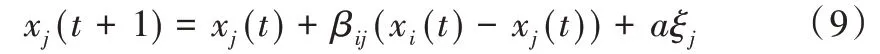
其中，t为算法迭代次数，a为步长因子，ξj为标准正态分布U（0，1）的值。

2.2 改进方法

标准的FA 在实际应用中存在以下问题：

（1）如果多维空间中各维度取值范围和求解精度不同而依旧使用统一的步长因子，会导致各维度无法在同一迭代次数达到最优解。

（2）随着算法迭代次数增加，萤火虫个体聚集于最优解附近时，如果使用固定步长因子来更新位置会因为步长因子过大使得萤火虫移动距离过大，导致萤火虫在最优解位置附近振荡［20］，无法收敛解出最优解，影响算法的效率和求解精度。

针对以上问题，本文在标准FA 上进行改进。

对于问题（1），在d维空间中，通过引入a→=(a1,a2,a3...ad)取代a，称为步长向量。根据不同维度的范围和精度设置不同的步长向量。

对于问题（2），本研究在标准萤火虫算法基础上，随着萤火虫逐渐接近最优解逐步缩小步长因子。开始迭代时，将a设为较大值，执行迭代时步长因子调整为：

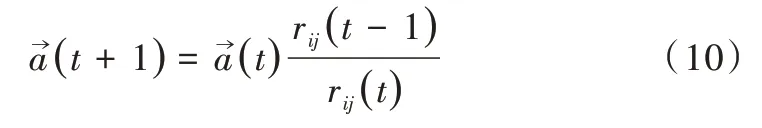
这样，步长因子会根据萤火虫距离的缩短而减小。当算法接近最优解时能保持有效的收敛速度，这种改进的萤火虫算法简称为MFA（Modified Firefly Algorithm）。

2.3 优化船舶横摇曲线参数

式（6）中经参数简化后的船舶横摇运动方程有θm、μθ、nθ三个未知参数，要获得未知参数的最优解，本文将拟合结果与实际数据的残差平方和最小作为评估标准，即：

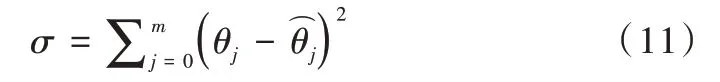
式中，θj为横摇倾角实际值，为根据拟合获得的横摇倾角，m为横摇倾角序列数据量。

利用MFA 求解船舶横摇参数的主要步骤和算法流程如图1 所示。

流程如下：①设置FA 基本参数，包括萤火虫数目、步长因子a初始值、光吸收强度系数γ、最大吸引度β0、最大迭代次数；②初始化萤火虫位置X={x1,x2,x3...xn}；③导入经处理后的横摇倾角数据{θ1,θ2,θ3...θj}；④根据式（8）计算出萤火虫间的吸引度；⑤根据式（11）更新步长因子；⑥根据式（9）更新萤火虫位置；⑦判断是否达到最大迭代次数，或残差平方和小于设定值，如果是，执行下一步，否则返回步骤④；⑧输出θm、μθ、nθ最优解。

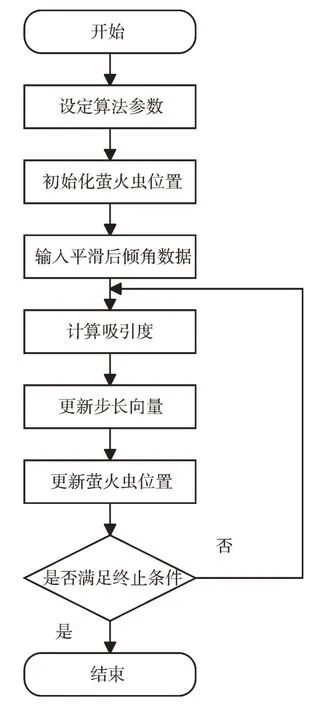
Fig.1 Flow of the proposed MFA图1 MFA 算法流程

3 实例应用及结果分析

3.1 准备工作

数据采集系统结构如图2（彩图扫OSID 码可见，下同）所示，以某集装箱船舶为例，使用两轴倾角传感器采集船舶倾角信号，通过ZigBee 无线模块将采集信号传输到上位机。上位机软件使用LABVIEW 编译环境。船舶基本信息如表1 所示。

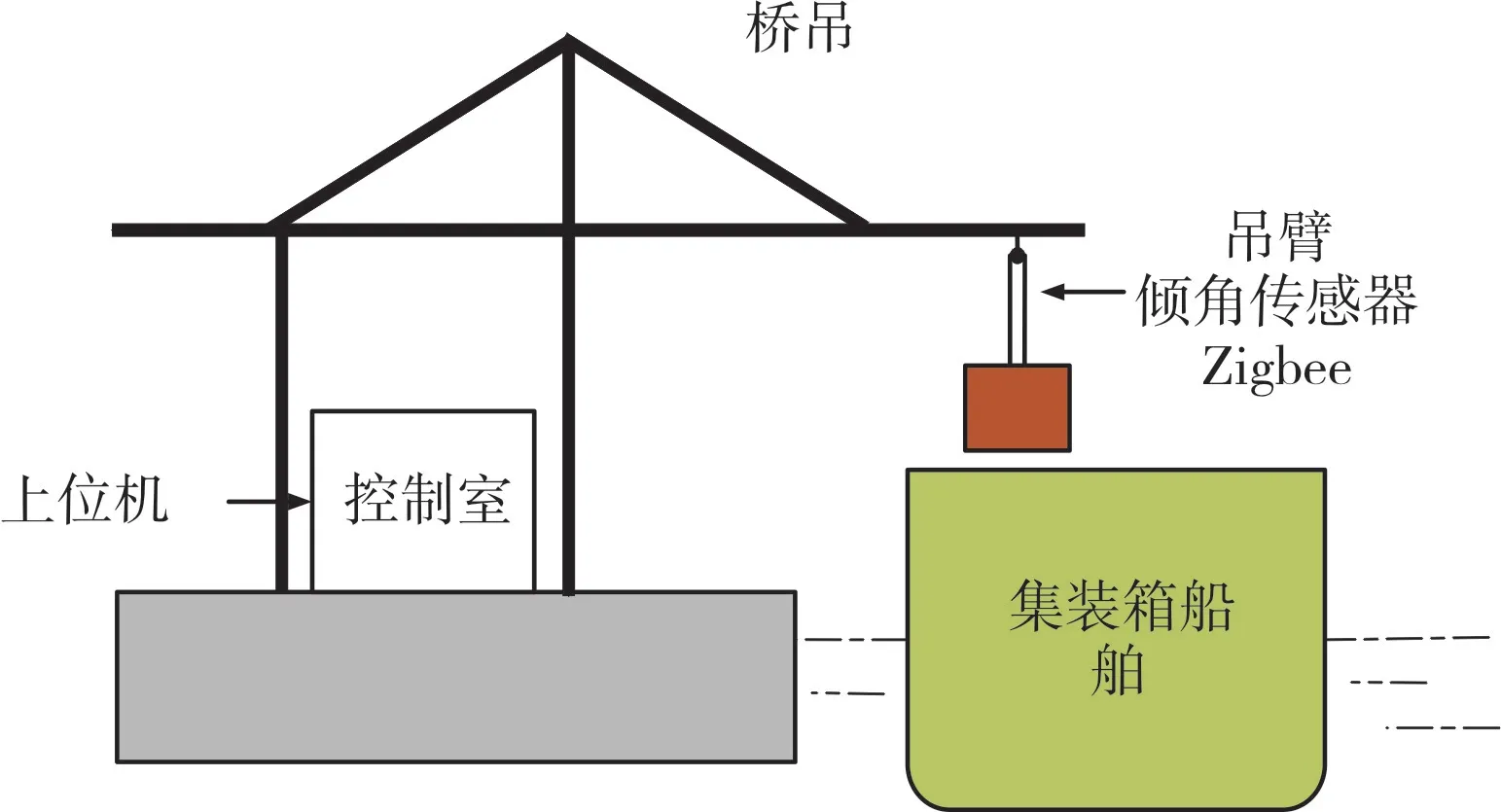
Fig.2 Schematic diagram of the data acquisition system图2 数据采集系统结构

Table 1 Basic information of one ship表1 某船舶基本信息 （m）

实验前需要将两轴动态倾角传感器进行水平校准，然后将其安装在吊具上，当吊具着箱时开始采集倾角信号，起箱时结束采集，所得倾角信号通过ZigBee 无线模块发送至上位机进行处理，系统主程序采用LabVIEW 编程环境开发，参数优化程序采用MATLAB 脚本节点编写。

本文实验仿真内容如下：

（1）利用标准萤火虫算法FA、MFA 分别优化不同装载状态下的横摇倾角数据，证明利用参数优化思想分析船舶横摇的可行性。

（2）对两种算法进行50 次优化，分析优化结果和算法误差，对比分析MFA 算法的优越性。

（3）改变横摇倾角数据量，分析不同数据量下MFA 优化结果精度，分析最优数据量。

3.2 算法可行性分析

在进行算法计算之前需设定初始参数，本实验中FA 和MFA 算法参数如表2、表3 所示。

Table 2 Parameters settings of MFA表2 MFA 算法参数设置

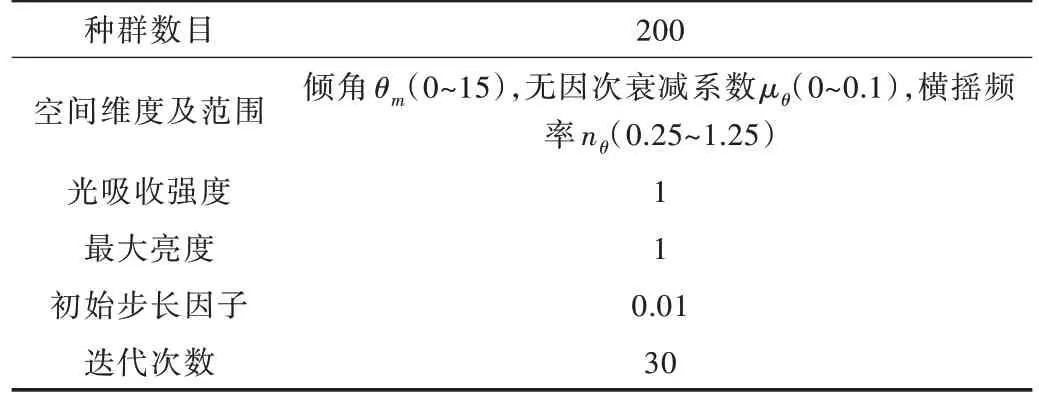
Table 3 Parameters settings of FA表3 FA 算法参数设置

从图3、图4 可以看出，FA 和MFA 两种算法对不同装载状态下的船舶横摇运动均能实现曲线回归。半载和满载状态下船舶横摇呈现为衰减的正弦曲线，符合船舶横摇运动方程的描述，且满载时横摇周期较长，符合船舶横摇运动原理。当FA 和MFA 算法迭代次数相同时，可以很明显地看出MFA 拟合曲线与原数据更为贴近，FA 优化曲线相较于真实值有明显的偏移现象。

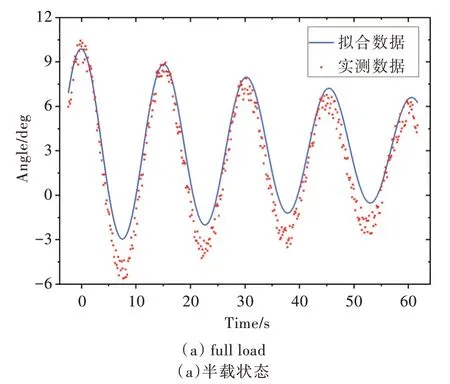
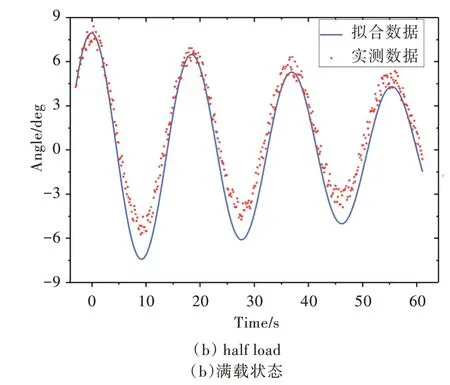
Fig.3 Fitting results of normal FA图3 标准FA 算法拟合结果

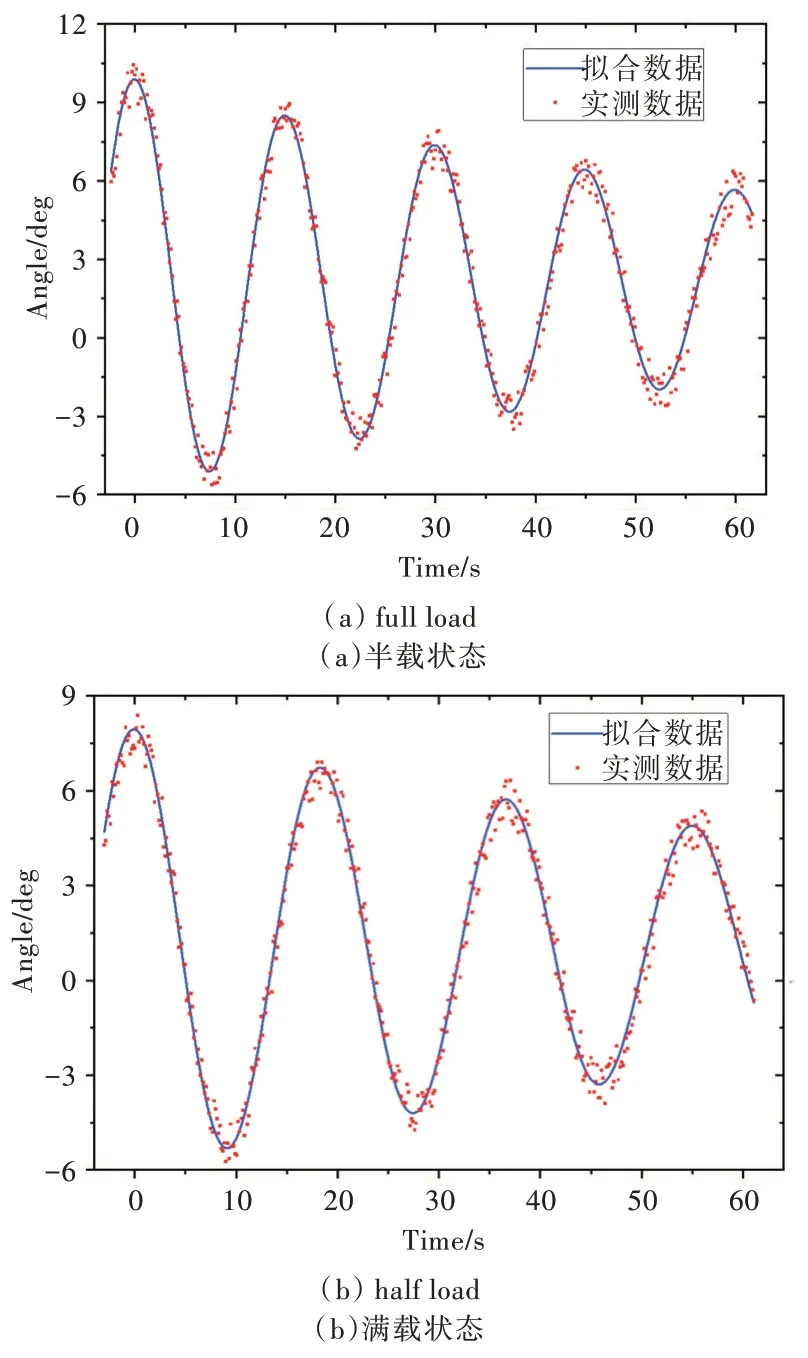
Fig.4 Fitting results of MFA图4 MFA 算法拟合结果

由此可以判断，利用参数优化思想结合船舶横摇运动方程来分析船舶横摇运动的方法是可行的。利用一定长度的横摇倾角数据训练船舶横摇运动模型，当算法收敛到最佳拟合时可求解到横摇运动曲线参数。同等迭代次数下对比FA 和MFA 结果，可以初步得出解算精度与使用的算法和算法参数相关的结论。

3.3 MFA 优越性分析

萤火虫算法优化精度与迭代次数相关，随着迭代次数的增加，解算结果收敛于最佳值，优化精度也随之提升。为分析MFA 相较于标准FA 的优越性，本实验基于3.2 节设定的参数进行50 次优化，分析参数优化均值和相对误差。

表4 是两组数据50 次优化结果的平均值。表4 显示，横摇运动倾角峰值和无因次衰减系数与装载状态相关性不大，而振动周期随着船舶装满而变大，符合船舶横摇基本原理。当两种算法迭代次数相同时，MFA 算法计算精度优势明显。其中，半载时拟合曲线与原数据决定系数为0.972 2，满载时决定系数为0.984 1，表明拟合结果具有极高的可靠性。而标准的FA 最大相对误差和平均相对误差都大于MFA，决定系数也相对较低，说明标准FA 在同等迭代步数下的优化结果精度比MFA 更低。实际上增加迭代步数同样可以使FA 的优化结果达到MFA 的效果，不过这需要更大的计算量，由此对比体现出MFA 的优越性。

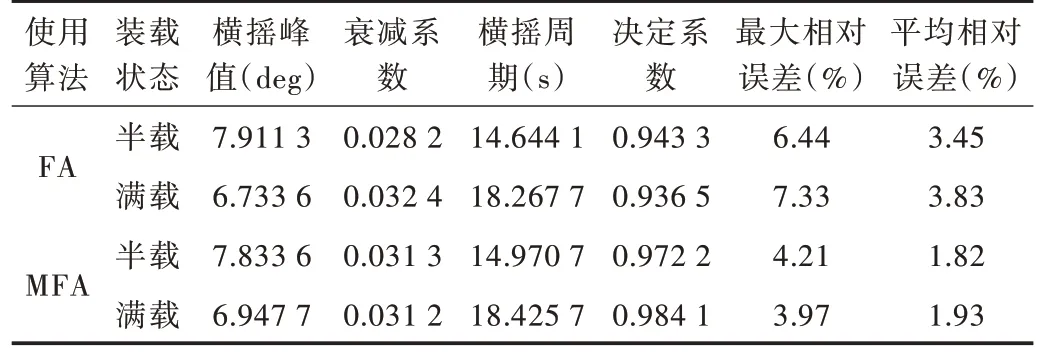
Table 4 Optimization results of MFA and FA parameters under different loading conditions表4 不同装载状态MFA、FA 参数优化结果

3.4 实测数据量对优化结果影响分析

在港口实际工作中，吊臂具着箱过程时间短暂，所采集到的实际倾角数据量有限。为实现在有限的实测数据内求解最优结果并进行横摇运动预测，需要分析实测数据量对拟合结果的影响，在尽可能少的数据量情况下拟合出可靠性高的横摇运动曲线。

本实验中横摇倾角采样周期为0.15s，船舶为满载状态，横摇周期约为18.4s，为分析实测数据量对优化结果的影响，本实验分别对1/4、1/2、3/4、1 个周期的数据进行模型参数优化。

图5 显示，当代入算法的实测数据为T/4 时，在T/4 时间后拟合结果与实测值有很大误差，优化模型无法准确预测横摇运动。代入算法的数据量为T/2、3T/4、T 时，优化模型的预测结果与实测值有极高的吻合度。结合测量船舶实际横摇倾角的工作环境，使用T/2 的实测数据训练模型，优化横摇运动模型参数最为合适，其优化结果预测横摇运动有很高的可靠性。

MFA 作为一种群智能算法，优势在于能从维度空间各个方向收敛，相对于传统的优化算法有着更快的迭代速度［21-23］，算法在迭代开始时就能自动分为多个子群，子群聚集在局部最优解附近，通过局部最优解的比对寻找到全局最优解。MFA 速度快、精度高的特点适用于优化船舶横摇运动模型参数，并预测横摇运动状态。但在实例实验中，当局部最优解与全局最优解位置接近时，存在求解结果为局部最优解情况，该问题有待进一步研究。

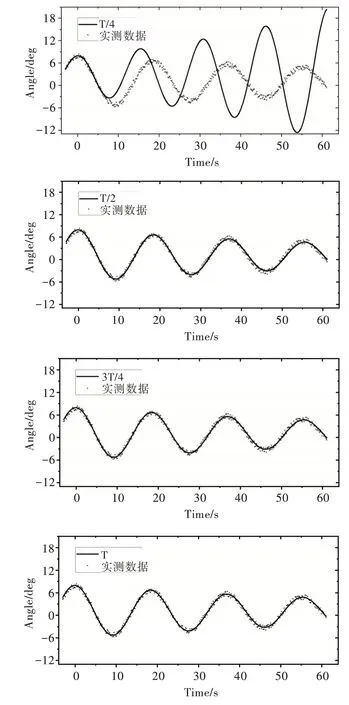
Fig.5 Fitting results with different data volumes图5 不同数据量的拟合结果

4 结语

本文通过解算船舶横摇参数求解初稳性高的方法分析系泊船舶装卸作业工况下的稳性问题，并针对横摇方程提出基于改进萤火虫算法的优化方法。该方法提高了求解效率，改进了步长向量和步长更新算法。通过实验验证了该方法的可行性。对比迭代30 次情况下MFA 相较于FA的优越性。实验表明，MFA 算法能够在较短时间内较好拟合不同装载状态下的船舶横摇运动曲线。在半载情况下，拟合结果与原数据决定系数为0.972 2，满载情况下为0.984 1，拟合结果具有很强的可靠性。结合实际工况分析了训练模型的实测数据最合适的数据量为T/2。该方法将智能群优化算法运用到船舶横摇运动状态预测，为系泊船舶装卸作业的稳性分析和预测提供了解决方案。