初始化参数对RRT 算法性能影响研究
冯 蕊,杨雪锋,2
(1.重庆交通大学 航运与船舶工程学院,重庆 400074;2.交通安全应急信息技术国家工程实验室,北京 100011)
0 引言
随着移动机器人技术的发展,路径规划算法得到深入研究和广泛应用[1-2]。遗传算法、模拟退火算法等传统路径规划算法需要对障碍物进行精确的数学建模,对于复杂环境中的规划问题处理效果较差[3],且多数算法未考虑移动机器人的非完整性约束限制[4],使得规划路径不一定可执行。
针对复杂空间建模困难和非完整性约束考虑不足问题,1998 年LaValle 等[5]、唐华斌等[6]提出快速搜索随机树(Rapidly-exploring Random Tree,RRT)算法,该算法采用随机采样方法,不需要对状态空间进行预处理和建模,而且在搜索过程中还考虑了机器人客观存在的约束条件,如非完整性约束、动力学约束、运动学约束等,从而能有效解决复杂环境问题,得到越来越多研究人员的关注。
RRT 算法通过随机采样以逐步迭代的方式进行随机树构造,通过从根节点以步长λ不断扩展出叶子节点的方式构建随机树[7]。由于采用随机采样的方式进行路径规划,RRT 算法中随机树的指向性较差,导致收敛速度较慢且规划结果通常不是最优。针对此问题,2000 年Kuffner等[8]又对随机树生长策略进行改进,在生长过程中以一定的概率将目标点直接作为随机采样点(以下简称偏置概率Pg),这既能提升收敛速度,也能降低规划路径长度,大大提高了RRT 算法效率。可见,步长λ和偏置概率Pg这两个初始化参数与RRT 算法性能密切相关,选择合理的初始化参数能够提升收敛速度,优化路径规划结果;反之则会增加算法耗时,使规划结果变差。同时,针对不同复杂程度的规划任务空间,初始化参数选择也不尽相同。现有的RRT算法及其改进算法在设置生长步长和偏置概率时主要依据研究人员的经验,缺乏相应依据。
为揭示初始化参数对RRT 算法性能的影响规律,并为初始化参数选取提供依据,本文通过计算机模拟不同复杂程度的路径规划任务空间,对规划结果进行统计,分析初始化参数对RRT 算法性能的影响。
1 研究现状
针对RRT 算法收敛速度慢和规划结果不是最优的不足,相关学者提出了多种基于RRT 算法的改进算法,但关于RRT 算法初始化参数对RRT 算法性能影响的研究还较少。李猛[9]在对无人机任务规划中的航迹规划和任务分配问题进行研究时,通过研究不同障碍物环境下RRT 算法中步长对其算法性能的影响,提出利用混沌序列生成随机节点,利用模糊推理系统动态调整算法参数的改进RRT 算法。这种改进RRT 算法通过查询模糊推理表,针对不同的障碍物环境更新偏置概率Pg和步长λ这两个参数来提高RRT 算法的性能,从而优化RRT 算法路径规划结果;路引等[10]针对RRT 算法的步长λ对RRT 算法影响进行探讨,最后设计了基于RRT 算法的无人机航路在线规划方法。该项研究通过理论分析说明了RRT 算法步长对其性能的影响;冯来春[11]针对路径规划算法的运动学约束和普适性两方面问题,提出了基于引导域的参数化RRT 运动规划算法。该算法在节点采样时以一定的概率采用激进的采样方式,加快随机树向外扩展速度;在节点扩展时以一定概率采用目标偏置扩展策略,加快随机树向目标位置扩展的速度,该项研究主要从RRT 算法的参数采样概率Pg来优化RRT 算法性能。
目前专门针对RRT 算法参数的研究还较少,实际应用中一般通过经验试凑来选取RRT 参数。因此,本文拟通过计算机模拟方法构造不同复杂程度的任务空间,研究初始化参数步长λ和偏置概率Pg对RRT 算法的耗时t、路径长度L、规划失败概率Pf等5 个方面性能的影响,为RRT 算法在移动机器人技术领域更加广泛的应用提供依据。
2 RRT 算法概述
采用RRT 算法进行路径规划主要步骤如下:
(1)将出发点作为随机树T根节点。
(2)产生一个0~1 之间的随机数x,如果x小于偏置概率Pg则将目标点Cgoal作为随机采样点Crand;否则在状态空间中随机选择一点作为Crand。
(3)寻找随机树T中与Crand最近的节点Cnear,并根据步长λ计算得到叶子节点Cnew。
(4)判断Cnear与Cnew之间是否存在障碍物,若不存在障碍物则将Cnew作为T的子节点,添加边[Cnear,Cnew];否则,返回步骤(2)。
(5)当随机树中存在叶子节点与Cgoal之间的距离小于步长且无障碍物遮挡,便可在随机树中找到一条由节点组成的从出发点到目标点的路径[12],RRT 算法路径规划过程如下:

相对于其他算法,RRT 算法需要设置的参数较少。通过对RRT 算法分析可知路径的起始点Cinit和目标点Cgoal是固定的,而采样概率Pg和步长λ的取值将影响Crand、Cnear、Cnew,即影响规划路径的长度L和算法耗时t,也影响路径规划的失败概率Pf,从而影响规划路径结果好坏和算法的实时性[13-14]。因此,针对不同的任务空间,本文设置不同的λ和Pg,RRT 算法参数与性能指标关系如图1 所示。
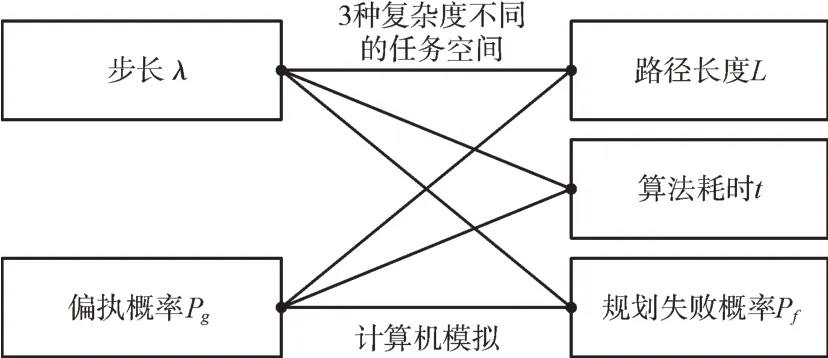
Fig.1 Relationship structure between RRT algorithm parameters and performance indicators图1 RRT 算法参数与性能指标关系结构
RRT 算法各个性能指标含义如下:①路径长度L指沿着规划结果从出发点到目标点连线的长度之和;②算法耗时t指计算机完成1 次路径规划所耗费的时间;③规划失败概率Pf指进行100 次路径规划至算法运行结束时仍未获得规划结果的次数。
3 仿真实验
3.1 任务空间
为揭示初始化参数对RRT 算法性能的影响,本文借鉴文献[15]的方法构建3 种不同复杂程度的任务空间,分别为简单任务空间、一般任务空间和复杂任务空间,所有任务空间大小均为100×100 的无量纲二维区域,出发点位置为(0,0),目标点位置为(100,100)。3 种任务空间中障碍物个数分别为20、50 和100,且所有障碍物均为圆形区域。随机从1、2、5 三个数值中随机选择一个作为半径,圆的位置在任务空间内随机产生。因此,不同任务空间中障碍物覆盖区域半径的均值相同,障碍物个数可以反映任务空间的复杂程度,3 种复杂程度不同的任务空间如图2 所示。
3.2 步长λ 对算法性能的影响
采用RRT 算法对上述不同任务空间中的路径规划进行仿真实验。仿真软件平台为MATLAB2016,在100×100的任务空间内对3 种不同复杂程度的任务空间分别设置步长λ为2~20,间隔为2,共进行10 组仿真实验,每组分别进行100 次路径规划。仿真实验中,偏置概率Pg设置为0.5。当程序连续产生500 个随机采样点均无法进行随机树扩展,或者在随机树扩展时生长点与障碍物碰撞次数累计达到100 000 次,则认为本次路径规划失败。仿真实验结束后取各性能指标的平均值作为结果进行统计分析,仿真实验结果如图3 所示。
在图3(a)中,所有任务空间中耗时t均随着步长λ增大而减小,可见增加步长有利于提高RRT 算法的实时性,而且任务空间复杂程度越高,进行路径规划耗时越长,实时性越差,任务空间的复杂程度对RRT 算法实时性存在显著影响。

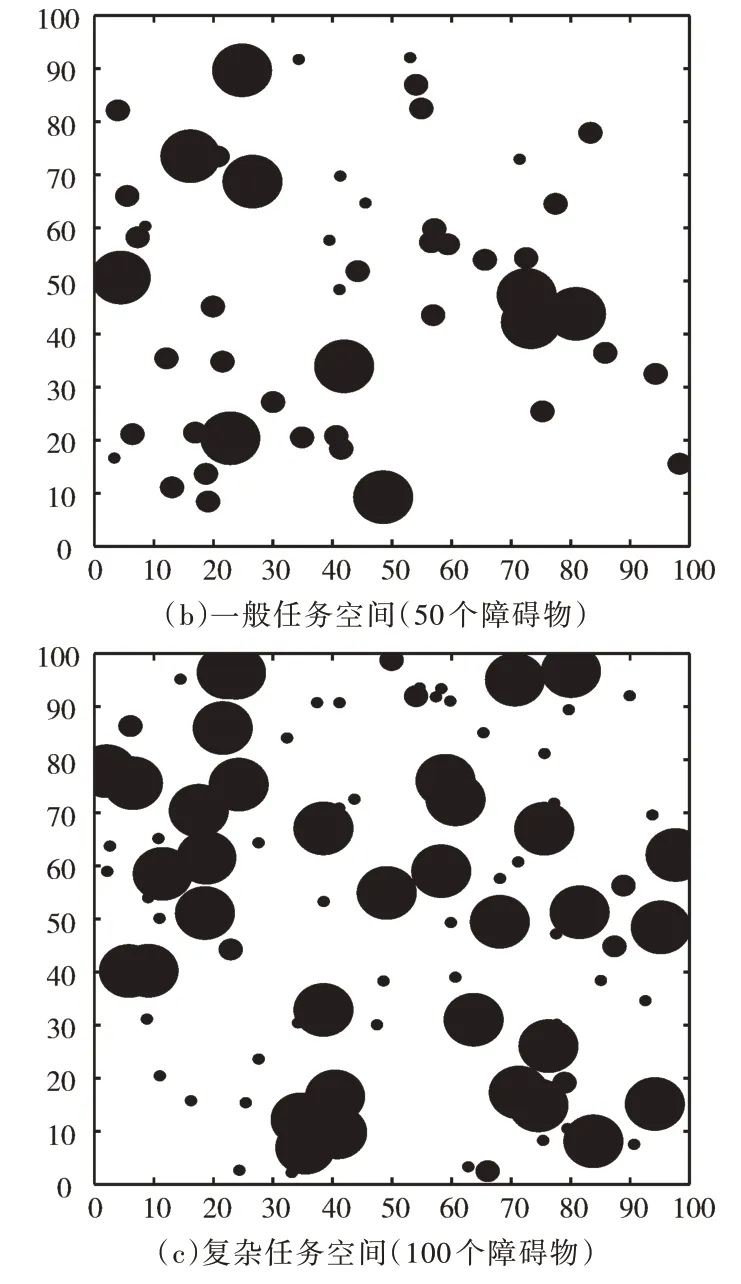
Fig.2 Task space with different complexity图2 不同复杂度的任务空间
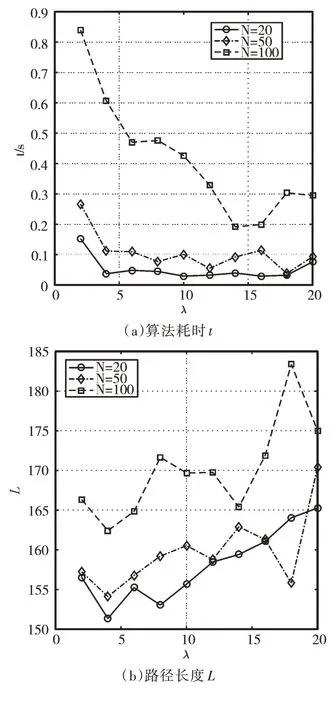

Fig.3 Changes of RRT algorithm performance with step size图3 RRT 算法性能随步长的变化情况
在图3(b)中,随着步长增加路径长度也逐渐增加,这说明降低RRT 算法中的步长有利于获取更优的路径规划结果(规划路径更短)。可以看出,仿真时间和路径长度随步长的变化规律刚好相反,步长既不能太大也不能太小,应综合考虑其对耗时和规划结果两方面的影响。
从图3(c)可以看出,即使对于简单的任务空间RRT 算法也可能出现路径规划失败的情况。并且随着步长增加,路径规划失败的概率也进一步增加。对于构建的3 种任务空间,当步长为20 时路径规划失败概率超过80%。同时,随着任务空间复杂程度的增加,路径规划失败的概率也会增加。
总体上RRT 算法中步长λ对算法耗时、规划结果(规划路径长度)、规划失败的概率均有直接影响。增加λ算法耗时会得到一定程度的降低,但路径长度和规划失败的概率会有一定程度的增加,在工程应用中应根据实际需求综合考虑步长对这3 方面性能的影响。
3.3 参数Pg对算法性能影响
在研究偏置概率Pg对算法性能影响仿真实验过程中,仿真软件平台、任务空间、终止条件等试验条件与前述内容一样。
步长λ设置为5,偏置概率Pg大小为0.05~0.95,间隔为0.1,共计10 组仿真实验,每组分别进行100 次路径规划,取各性能指标的平均值进行统计分析,仿真实验结果如图4所示。
从图4(a)可以看出,在一般任务空间(N=50)和复杂任务空间(N=100)中算法耗时随偏置概率Pg的变化规律几乎相同,均是先减小再增大,这是因为当偏置概率较小时随机树生长的目标性不强,产生了过多的随机采样点;当偏置概率较大时,将目标点直接作为随机采样点的概率较大。若目标点与出发点之间存在障碍物阻挡,则随机采样失败概率较高,导致耗时增加。对于简单任务空间(N=20),较大的偏置概率不会引起算法耗时增加,如当Pg=0.95时,耗时t=0.11s,仅比最低耗时0.1s 多0.01s。这是因为在简单任务空间中,出发点和目标点之间的连线上障碍物较少,将目标点作为随机采样点是合理的,有利于提高路径规划效率。

Fig.4 Changes of different performances of RRT algorithm with parameter Pg图4 RRT 算法的不同性能随参数Pg的变化
在图4(b)中,3 种复杂程度的任务空间中路径长度L随偏置概率的变化趋势完全一致,均随着Pg的增大后路径长度逐渐减小,规划结果更优。这是因为随着Pg增大路径主要朝着目标点进行生长,朝其他方向生长的概率降低,因而路径的转向点个数减少。
在图4(c)中,随着偏置概率增大,路径规划失败的概率也逐渐增大,因此偏置概率不能设置得太大。尤其是对于复杂的任务空间,较高的偏置概率将导致路径规划失败,如图4(c)中Pg>0.75 时始终难以获得路径规划结果。
总的来讲,偏置概率越大,随机树生长的目的性越强,算法消耗时间越短,规划结果中路径长度越短。但是,如果偏置概率过大,则随机树朝其他方向生长的可能性很小,如果任务空间的障碍物较多就可能导致路径规划失败。综合考虑算法耗时、路径长度和规划失败率,将偏置概率设置为0.5 比较合理。
3.4 实验结果分析
根据RRT 算法路径规划试验统计结果可知,随着步长增大,路径规划耗时将减小,但规划的路径长度和规划失败的概率将提升;随着偏置概率增大,路径规划耗时呈现出先减小再增大的趋势,规划路径长度减小但路径规划失败的概率增大。初始化参数对算法性能影响情况如表1 所示。
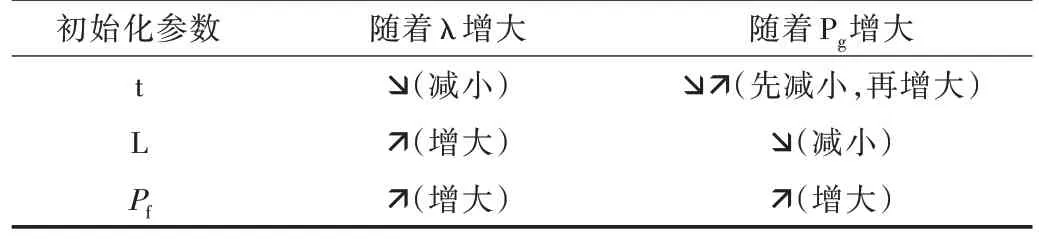
Table 1 Influence of initialized parameters of RRT on algorithm performance表1 RRT 算法初始化参数对算法性能的影响
4 结语
为了揭示初始化参数对RRT 算法性能的影响规律并为参数选取提供依据,本文通过计算机模拟不同复杂程度任务空间中的路径规划问题,构建3 种不同复杂程度的任务空间。对仿真实验结果分析得出以下结论:
(1)初始化参数步长和偏置概率对算法的性能存在显著影响,应根据实际需求和任务空间的复杂程度两方面确定初始化参数。
(2)算法耗时和路径长度这两个性能指标随步长的变化规律刚好相反,其中一个性能指标变好,则意味着另一个性能指标变差。因此,设置步长时应综合考虑这两方面需求。
(3)偏置概率的设置应考虑任务空间的复杂程度,对复杂度较高(障碍物个数较多)的任务应设置较小(障碍物个数较少)的任务空间;若任务空间复杂度较低,则可设置较大的偏置概率。

