往复压缩机撬座隔振器的设计方法
祁豪杰,洪 坤,何 睿,贾晓晗
(1.西安交通大学能源与动力工程学院,陕西西安 710049;2.盈德气体集团有限公司,浙江杭州 310000)
1 引言
往复压缩机工作过程中存在不平衡的惯性力和力矩,导致整机或者基础振动,进而传递至关键设备时,将可能导致严重的安全隐患,隔振是减少这种危害的常用方法。所谓隔振,是指在振源与被保护设备之间用隔振元件连接,减少振动的传递,从而减弱被保护设备的响应。隔振的目的主要是减小振源与被保护设备间的振动耦合,但与此同时会出现一些负面的影响,例如振源本身的振动可能增大、振源与被保护件的相对位移增大、安装及生产成本增加等,但在很多情况下,如果对多方面参数进行综合优化并采取相应的配套措施可以获得良好的隔振效果[1,2]。近年来,国内外的研究主要聚焦于海洋平台的隔振,包括导管架式海洋平台的阻尼隔振、基于柔性基础的浮筏隔振等[3-5],但对隔振器设计、撬座内外振动控制配套措施仍然没有形成一套具有指导性的设计方法与控制措施。因此,在总结工程经验的基础上发展一套隔振器设计的一般方法具有重要意义。本文借助山西盈德气体公司某机组仪器柜的隔振器项目,阐述了隔振器设计的一般方法,并采用有限元分析(FEA)方法,对设计结果进行了校核与分析。
2 隔振器的理论设计方法
隔振器的设计主要步骤包括确定隔振频率及隔振器的固有频率、确定撬座的参数、确定隔振器型式及参数、确定隔振器的布置方式等。针对某公司某机组仪器柜隔振项目,现场调研收集了相关数据,整理分析发现其最大振动值为9.17 mm/s,主要是由于仪器柜直接固定于压缩机机组的二层隔板上,机组振动通过隔板传递到仪器柜,导致了较大的振动。厂家要求将振动值降低至合格标准内,下面结合该项目,详细论述隔振器设计的主要步骤。
2.1 隔振频率及隔振器的固有频率
隔振频率f,也称激发频率,通常是指机械设备最严重的扰动力或力矩的频率,对于具有不平衡惯性力或惯性力矩的往复机械来说,则应取其最严重的不平衡扰动对应频率f。
隔振器的固有频率应根据相关设计要求,由给定的振动传递率TA或隔振效率I计算得出。公式(1)给出了隔振效率I、隔振系数η以及2个频率之间的关系。当未给定隔振效率时,一般应使扰动频率f和固有频率fn之比在2.5~5之间。
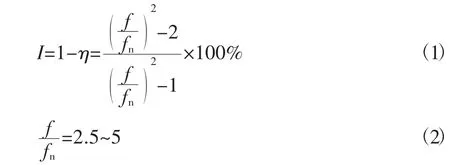
若上述条件不能满足,应选取尽可能小的fn,至少将其控制在f的70%以下。为防止发生共振,在常用转速范围内应让fn尽可能远离f。当弹性支撑的主要目的是隔声或缓冲时,fn的选择可在以下范围

某公司某二层平台离心空压机运行的额定转速为1494 r/min,对应的激振频率为24.9 Hz;为确保隔振效果,以隔振效率I不低于95%进行设计,通过式(1)可计算出隔振器固有频率应不高于5.434 Hz。
2.2 撬座的质量、刚度和尺寸
撬座的质量大小影响被隔振系统的振幅,当设备的弹性支撑在垂向独立时,质量与振幅的关系如式(4)所示。当振幅A超出容许值时,则应增加撬座质量以降低振幅A,使其满足要求。通常可把设备刚性地固定具有带有一定惰性快质量的撬座上,再用隔振元件连接撬座与基础,以达到增大质量降低振幅的目的。
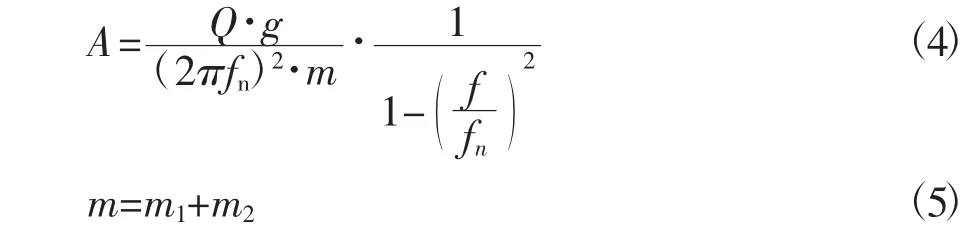
式中 Q——扰动力,kg
m——被隔振系统的总重量,kg
g——重力加速度,9.8 m/s2
m1——被隔振设备质量,kg
m2——撬座质量,kg
对于大、中型往复压缩机,在竖向、水平方向和绕旋转轴的回转方向均有较大的振动,因此为了满足隔振要求,隔振基础撬座的尺寸和重量都较大。一般来说,钢结构撬座基础的自振频率要避开隔振频率的3倍以上,撬座及附加质量要2~3倍于被保护设备的质量。撬座质量m2也可根据许可振幅和总扰力幅值计算得出,如式(6)所示
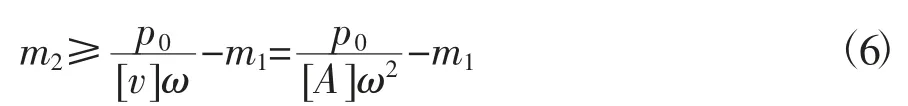
式中 [v] ——设备允许的振动速度,m/s
p0——隔振方向的扰力幅值,kg·m/s2
ω——干扰圆频率,rad/s
工程实际中通过增加惰性块的方式以增大撬座质量,在降低设备振幅的同时,还可以降低整体的固有频率和重心,提高隔振效果及稳定性;同时减少了重量分布不均匀及输出口反作用力的影响,较大的质量还能克服刚性低的部件的摇摆运动。
撬座材料的选择对刚度的影响较大,型钢制作方便,刚性大,但自重轻;混凝土刚性较好且重量较大,一般选择型钢做框架、内部做混凝土灌浆,以满足刚度和质量要求。撬座的几何形状通常是矩形,几何尺寸要根据现场实际条件决定,适应被隔振设备的尺寸、安装及操作条件等。
2.3 隔振器型式及刚度、阻尼
隔振器型式主要有橡胶隔振器、金属弹簧隔振器、空气弹簧隔振器等,一般根据所需垂向固有频率按以下标准选用:所需频率在5 Hz以上时,宜选用橡胶隔振器;3~5 Hz左右时,宜采用金属弹簧隔振器;低于3 Hz时,宜采用空气弹簧隔振器。确定隔振材料后,根据被保护设备的形状和所受激振力的类型及大小确定隔振器的具体结构。
隔振器所需总的垂向支撑动刚度可由隔振器固有频率fn及设备总重计算得出,如式(7)所示。
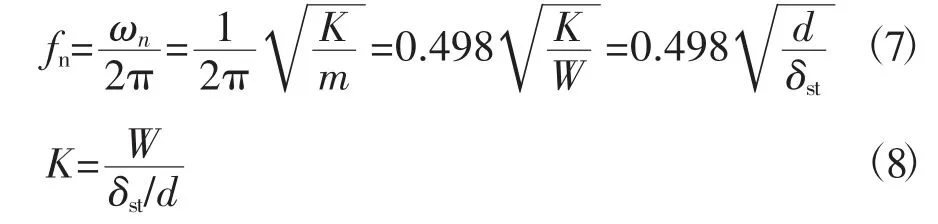
式中 K——垂向总刚度,kg/m
W——物体总重,W=mg
δst——工作状态的静挠度,m
d——隔振材料的动态系数,即隔振器的动、静刚度之比
一般材料d值的范围如表1。

表1 一般隔振材料的动态系数
图1描述了固有频率随动态系数与静挠度之比的变化关系,图2则描述了不同固有频率下,隔振器荷重与动刚度之间的关系。参考以上关系,有助于隔振器的准确快速选型。
隔振器的刚度可以根据固有频率由图1定出δst/d,再由式(8)确定K;也可以由图2根据隔振器荷重和固有频率查图得到刚度值。根据工程经验和相关文献[6],一般情况下,设备受到的水平扰动力相对较小,隔振器的水平刚度可略弱于垂直刚度,取为80%,有需要时可适当增加以应对水平方向振动。隔振器的数量要根据被隔振系统的尺寸以及机脚数量等确定,相邻的隔振器间距2~3 m为宜。
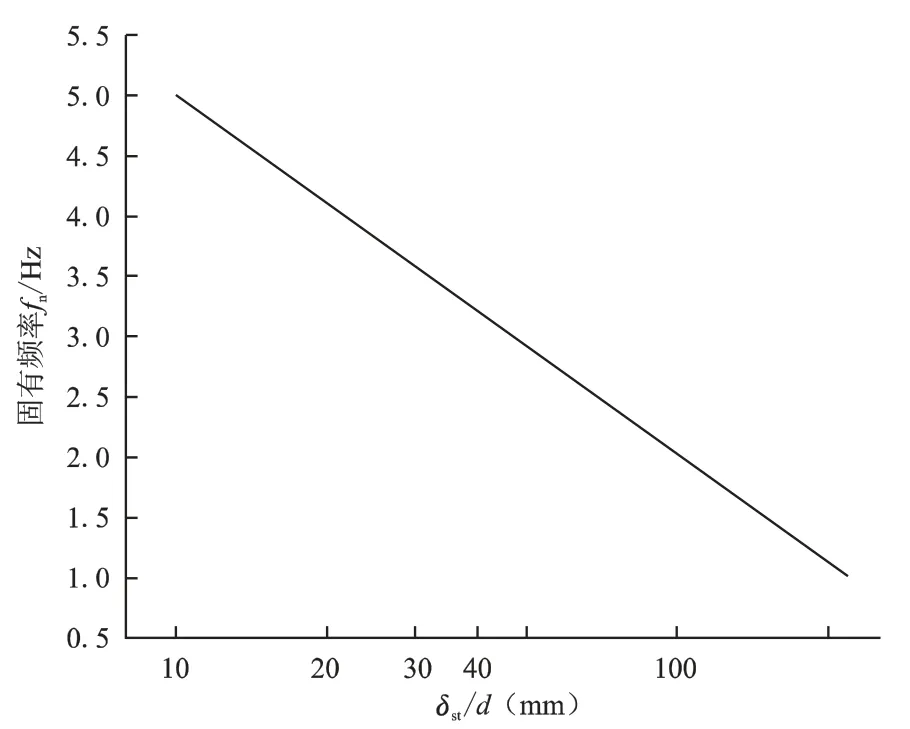
图1 固有频率随动态系数与静挠度之比的变化关系
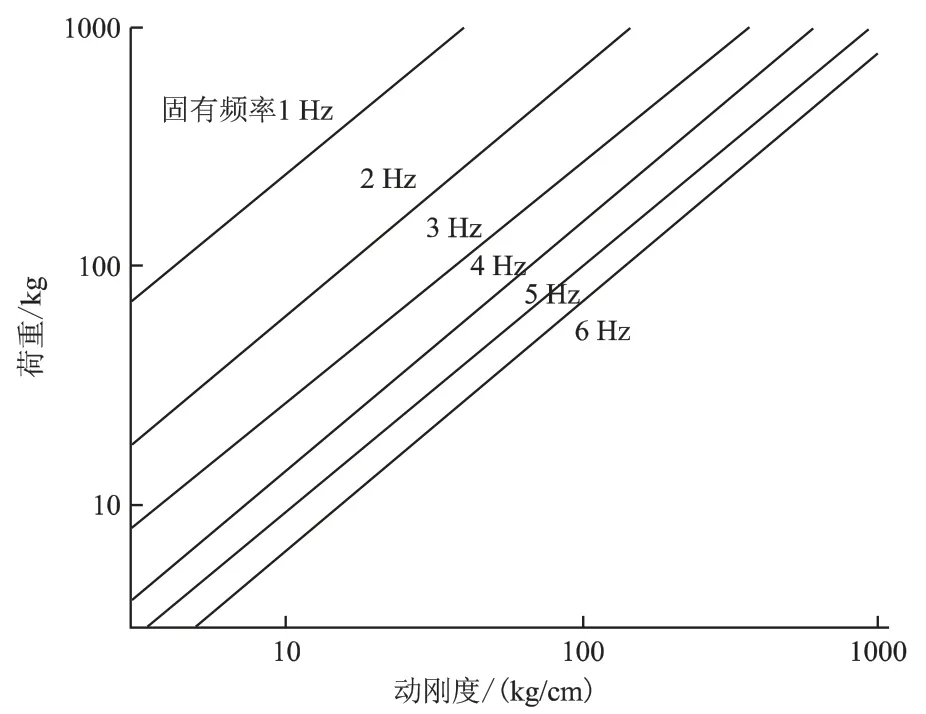
图2 不同固有频率下,隔振器荷重与动刚度之间的关系
由于隔振设计要求固有频率小于激发频率即fn<f,在设备启停过程中必然会经历扰动力频率等于固有频率的时刻,此时将发生瞬时共振现象。瞬时共振引起的最大振幅比稳定工作时振动的振幅大得多,可能危害生产安全,因此需要用阻尼来降低瞬时共振的振幅。启停过程一般大于5 s,激发频率大于10 Hz时,共振的振幅与稳定共振的振幅比较接近[6],为简化计算,假定二者相等,则瞬时共振的最大振幅可按式(9)求得

瞬时共振允许的最大振幅可取稳定振幅时的5~6倍,由此可确定隔振器的阻尼。

除了上述计算外,还可根据构造要求配置确定阻尼,即在垂向和水平向配置不小于0.05的阻尼比。应注意的是,水平阻尼可降低启动、停机和调速时的水平振动,提高设备运转时的平稳性,作用不可忽视。工程实践中常用的阻尼比范围为0.05~0.2。
在本案例中,隔振器固有频率不高于5.434 Hz,整个被隔振设备的总质量为1500 kg,代入式(7)可得出隔振系统需要总的垂向支撑刚度不超过2.08 kN/mm,以保证较低的固有频率。
在隔振器的刚度、阻尼等参数确定后,即可选型隔振器并进行强度校核。隔振器的承载力可按静载荷设计,但应留有裕量以应对受力不均等因素的影响,因此额定载荷应不小于工作载荷的1.25倍。选定隔振器后,根据最终确定的频率比,校验振动传递率是否符合要求。
2.4 隔振器的布置方式
目前对于隔振器的应用日趋普遍,但对于某一具体的隔振对象而言,特别是那些外形轮廓不规则,重心位置不对称的机组和设备,如何正确地布置隔振器,却不是都很清楚,因此发生了不少由于布置不当而引起的麻烦,致使隔振装置达不到预期的隔振效果。下面将对隔振器的布置进行简要介绍,主要归结为以下2点:
(1)尽力保证各个隔振器的载荷相同,以便采用相同型号的隔振器,且不能超出该种隔振器的许用范围,一般隔振器承受的载荷不仅和机组重量及重心位置有关,而且还取决于它本身的刚度。
(2)隔振器应尽量对称于机组的主惯性轴布置,以使刚度中心能与设备重心位于同一垂线或重合,从而避免引起耦合振动。当隔振体系重心与隔振器刚度中心重合于一点时,如图3的x、y、z、φx、φy、φz将均为单自由度振动体系,隔振体系模型如图4所示,在实际工程中一般较少采用这种方式。当隔振体系重心与隔振器刚度中心在同一铅垂线上,z与φz为单自由振动体系,x与φy耦合,y与φx耦合,隔振体系模型如图5所示,较易实现也是工程中常用的支承方式。

图3 坐标轴系示意图
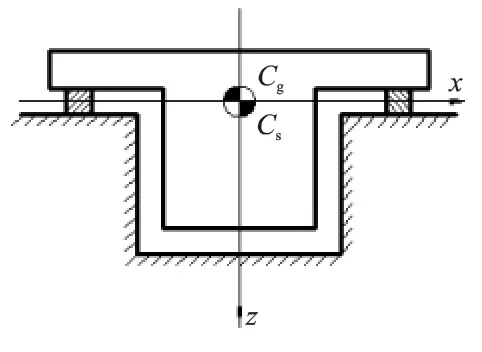
图4 单自由度体系
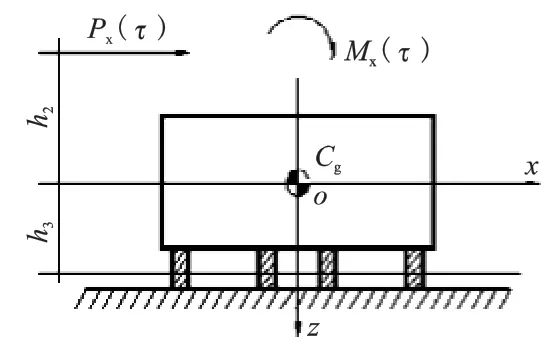
图5 水平回转耦合振动体系
在为压缩机组布置隔振器时,应参照要点2将刚度中心与系统重心设在同一铅垂线或重合,以保证垂向振动保持相对独立。为此,应在旋转轴投影的两侧布置隔振器,做到

式中 Ki——各隔振器的垂向刚度
Bi、Ci——距主惯性轴横向及纵向距离
若采用相同隔振器,则Ki为定值,上述方程可简化为

在工程实际中,由于设备的质量分布往往有一定的对称性,因此,可假定设备的外形对称轴即为主惯性轴。对应隔振器的不同选用方案,进行布置方案的讨论:
(1)采用相同的隔振器,需校核各个隔振器的荷载是否超限,若要求挠度也相等,考虑隔振器应如何布置;
(2)采用不同的隔振器,一般要求挠度需相等,考虑隔振器的刚度及如何布置。
无论采用以上哪种方案,都必须算出每个隔振器的荷载大小,以图6为例。
图6中oy轴及oz轴为设备的主惯性轴投影,设隔振器i的位置坐标为(Bi,Ci),载荷为Pi,刚度为Ki,挠度为δi,设备的总重量为W;隔振器位于oy轴两侧,成对布置,但位置不一定对称。
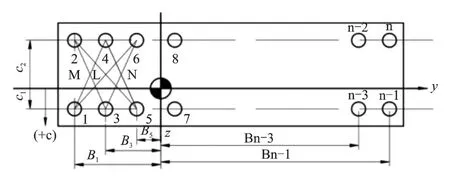
图6 多点支撑装置隔振器布置简图
由静平衡条件可得

由于各隔振器的顶端处于同一平面,故14连线、23连线在交点M处的挠度相等,即
式中,j=1,3,5……(n-3),k=6,8,10……n。若隔振器的刚度相同,则式(17)和(18)可变为

联立式(13)~(15)、(19)和(20)共n个方程式,可求出各个隔振器的载荷值,用以校核是否符合要求。若要求各隔振器的挠度也相同,则式(13)和(14)将变为式(12),这就是采用相同隔振器时,合理布置隔振器的条件。
如果采用不同型号的隔振器,则根据上述要求第二点,一般总是力求各隔振器的挠度δ相等,式(13)和(14)将变为式(11),然后根据所求出的各个隔振器的荷载值Pi,算出隔振器的刚度值,进而选择合适的隔振器,图7为采用不同隔振器的一种设计示例。
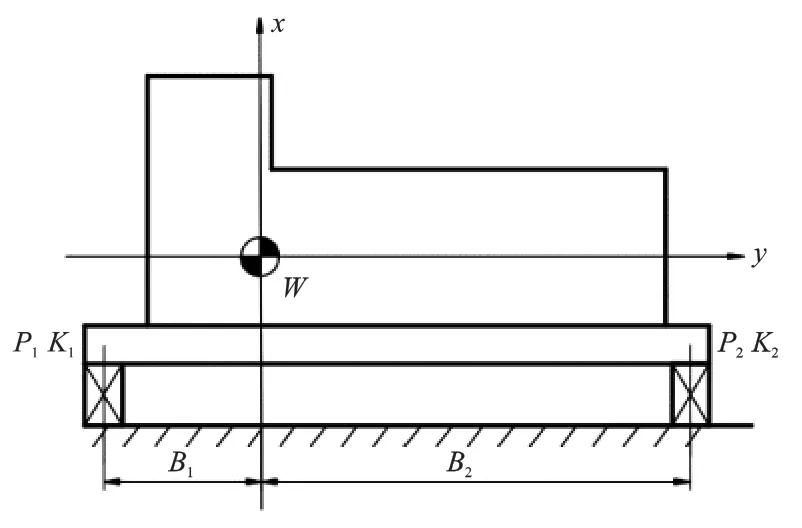
图7 采用不同隔振器的设计示例
下面就4点支撑结构,采用2种不同的隔振器选用方案的工程实例进行分析,4点支撑隔振布置如图8所示。
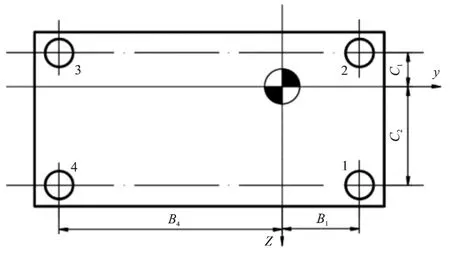
图8 4点支撑隔振装置
(1)采用相同隔振器
因为每个隔振器的刚度相同,所以各隔振器所承受的载荷如下(P1+P3=P2+P4)
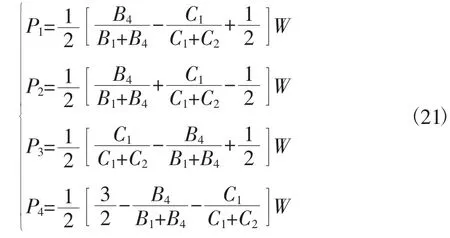
(2)采用不同隔振器
在实际工程中,如果机组或设备的重心偏置过大,以致不能采用同一种型号、规格的隔振器时,则必须在各个支撑点上选用不同的隔振器,以确保挠度相等。这时4个支撑点的载荷可按下式求出
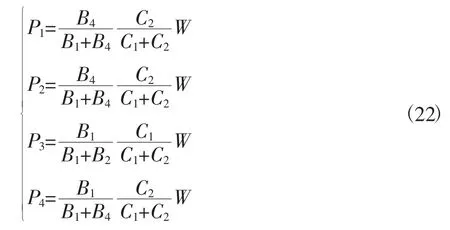
值得指出的是,对于隔振的设备,一定要保证其振动的自由。因此,凡是和外界相连的所有管路、连接轴、传动轴等,一定要做成挠性的,为此应采用蛇形软管、金属波纹管、弹性联轴器等弹性元件。柔性连接未作好,或者采用的是刚性连接时,不仅会降低隔振的效果,而且会使隔振基础上刚性连接点的对角点振动大幅增加。为防止安装在弹性支撑上的物体意外产生过大的相对位移,应在其周围布置一定数量的位移限制器,在正常情况下,它们是不接触的。
3 参数及计算结果
在本案例中,将空分仪器柜看作质量均匀分布,在质心落在主轴线上时,考虑布置8个相同型号的隔振器均匀分布在轴线两侧,再考虑到空分仪器在二楼的因素,将8个隔振器中的4个落在房梁处,减少薄弱楼板处的总承重。
将该空压机撬装及隔振系统设计参数汇总如表2所示。根据压缩机运行工况和隔振效率的要求(不低于82%),设计隔振效率选择为95%。设计的运行工况下机组总质量为1500 kg,其中撬内设备质量750 kg,撬座及增加的惰性质量为750 kg,其他设计结果见表3。

表2 弹簧隔振器设计参数

表3 弹簧隔振器设计结果
计算过程说明如下:
空分仪器柜总质量750 kg,根据经验,底撬质量应不小于撬上设备的1~1.5倍,故在底撬增加一惰性质量为750 kg的钢板,最终,含底撬的空分仪器柜总质量为1500 kg。
空压机转速为1494 r/min,激发频率为24.9 Hz,设计隔振效率定为95%,则根据公式(1)和(2)可计算出隔振器固有频率为5.434 Hz,总刚度为2.08 kN/mm。由于选用8个隔振器,故单个隔振器垂直刚度为0.26 kN/mm,水平刚度取为垂直刚度的80%,即0.208 kN/mm。
4 隔振器的选型及理论隔振效率校核
根据隔振分析设计报告计算数据进行核算后,最终选用瑞典某公司进口弹簧隔振器系列,该系列隔振器参数如表4所示,图9为该系列隔振器的垂直刚度变化曲线:
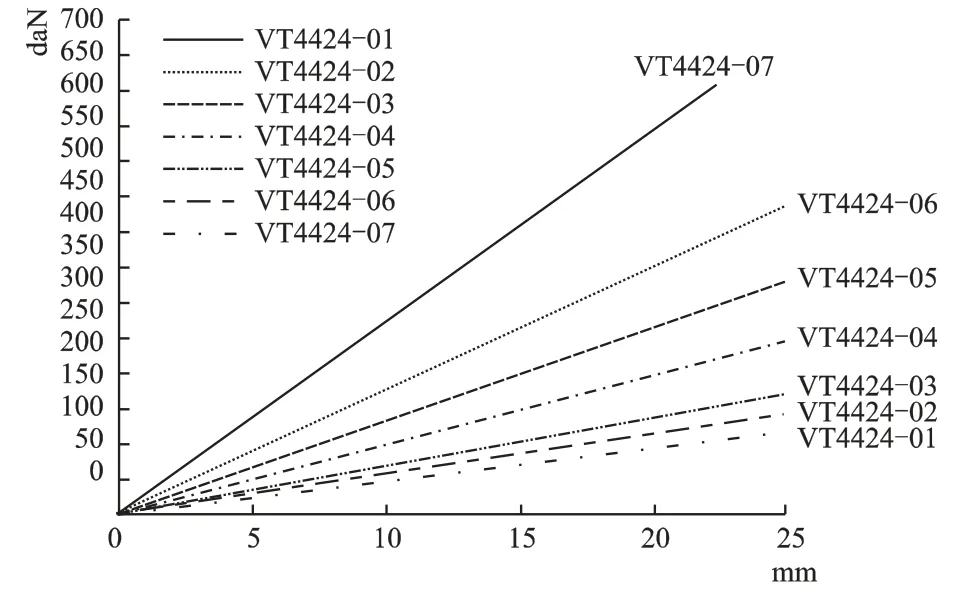
图9 某系列隔振器垂直刚度

表4 某系列隔振器参数
综合考虑不同型号隔振器的承载能力及其刚度,最终选用型号后缀为-04的弹簧隔振器,共8个,该型号隔振器载荷范围约为160~230 kg,垂向刚度为0.1 kN/mm,以该型号的弹簧隔振器参数对隔振效率进行核算如表5所示,最终隔振效率达97.7%。
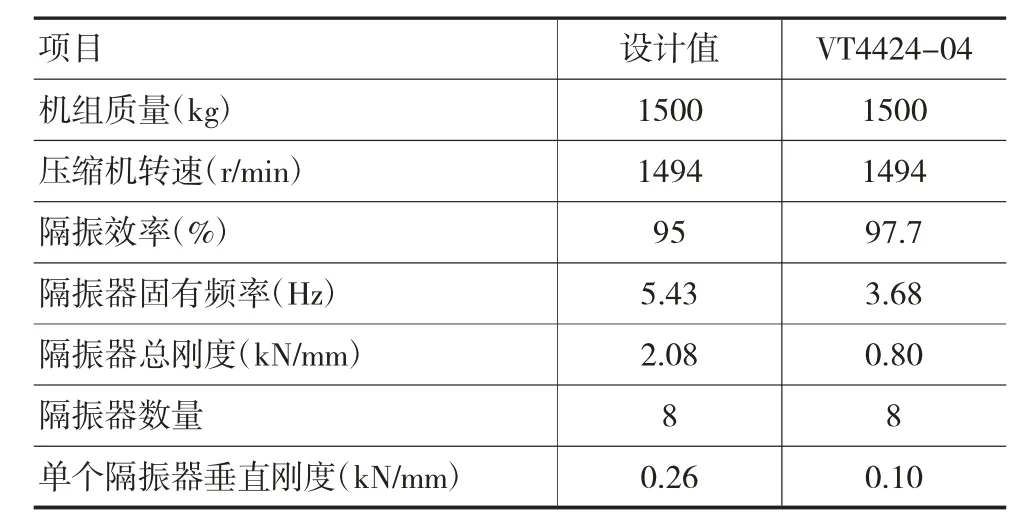
表5 隔振效率核算
增加隔振器和配重后,建立模型进行静力分析,以校核各个隔振器的压缩量是否合适,静力分析模型中仅需要考虑重力的影响,因此在模型中约束隔振器的下表面所有节点的自由度,并沿着重力方向施加重力加速度9.8 m/s2,分析模型如图10所示。

图10 静力分析模型
如图11所示为在重力载荷下隔振器及底撬的变形分布,从图中可以看出在重力载荷影响下的最大变形出现在隔振器上,由于隔振器弹簧被压缩所致,最大变形约为18.059 mm,符合要求。
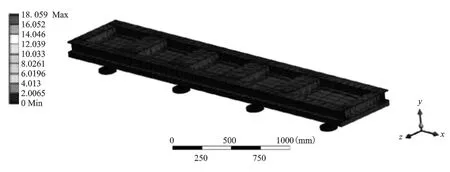
图11 重力载荷下底撬的变形
隔振器安装之后,压缩机组正常运行期间,仪器柜振动大大降低,所设计的隔振器隔振效果很好,达到了设计目的,项目验收顺利通过。表6列出了隔振器安装前后仪器柜各测点的振动值。
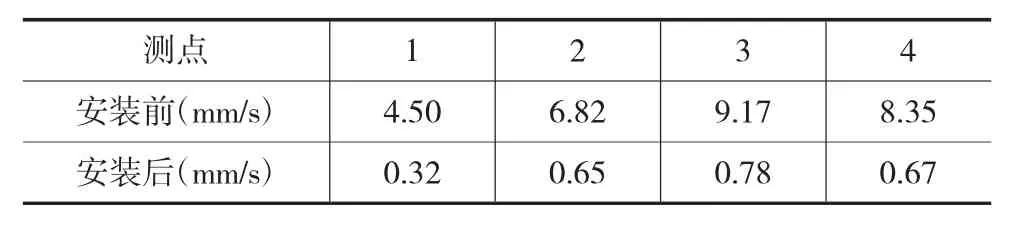
表6 隔振器安装前后仪器柜的振动值
5 结论
本文详细介绍了隔振系统设计的基本步骤,在此基础上完成了对某公司某仪器柜的隔振器设计和选型,并根据机组的质量分布规律确定了隔振器的基本布置方式,最后对隔振器的隔振效率进行了核算,核算后的隔振效率约为97.7%。采用有限元分析方法对所设计的隔振系统进行了静力分析,结果发现在重力载荷下最大变形量为18.059 mm,符合设计要求。隔振器安装后,隔振效果良好,将最大振动值由9.17 mm/s降低至0.78 mm/s,顺利通过验收。

