中小微企业的信贷决策研究
郑婉婷,李晓敏,李辰浩
(1.三峡大学,湖北 宜昌 443000;2.国网咸宁供电公司高新区供电中心,湖北 咸宁 437000;3.国网荆州供电公司监利县供电公司,湖北 荆州 433300)
1 中小微企业的信贷决策研究背景及内容
1.1 研究背景
随着我国经济的迅速增长及中小微企业数量的同步增长,中小微企业在国民经济中发挥着重要作用。为进一步加速中小企业发展,解决其资金难题,银行根据中小微企业的实际情况对其信贷风险作出评估,并根据信贷风险等因素确定信贷策略。
为了方便研究,假定银行的贷款额度为10~100 万元,年利率为4%~15%,贷款期限为1 年。收集并研究了123 家有信贷记录企业、302 家无信贷记录企业相关数据、贷款利率与客户流失率的关系。根据企业的实力、信誉等方面因素对无信贷记录的302 家企业的信贷风险进行量化分析,并确定银行在年度信贷总额定时对这些企业的信贷策略。
1.2 模型假设
假设一:银行贷款年利率与客户流失率的关系在任何情况下均保持不变。
假设二:银行对有违约记录的企业不予贷款。
1.3 符号说明
符号说明见表1。
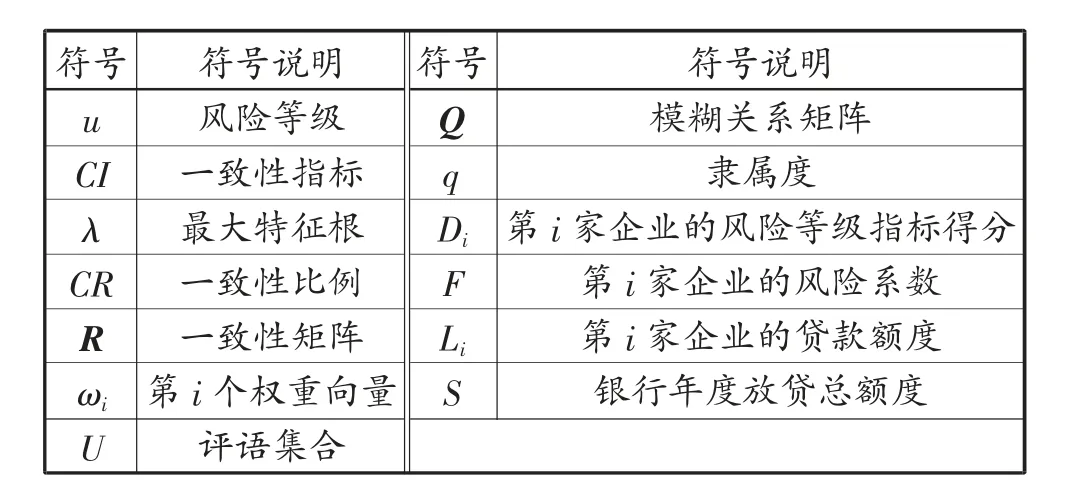
表1 符号
2 中小微企业的信贷决策研究数据分析
2.1 信誉等级
123 家有信贷记录企业信誉评级情况见图1。
据图1 显示,有19.51%的企业为D 级信誉(24 家),原则上银行不予进行放贷,此外,B 级、C 级企业中有3 家(E29,E45,E87) 存在违约记录,故不予进行放贷。
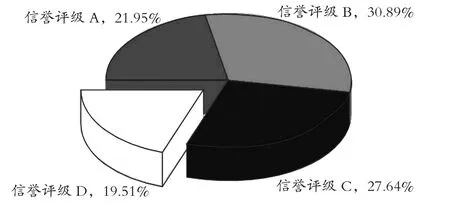
图1 123 家有信贷记录企业信誉评级图
2.2 企业信誉等级与营业情况
综合考虑企业信誉等级及营业情况,制得企业信誉与盈利间的关系图,见第48 页图2。
据图2 显示,同类型盈利企业信誉等级与公司利润间存在比较密切的关系:信誉评级为A 或B 的企业在大多数行业内盈利处于优势地位;数码、运贸、服务、营销、文化等行业企业在预贷款企业中利润额较大。考虑银行贷款利润,则优先放贷给预贷款同行业中或市场中优势企业。
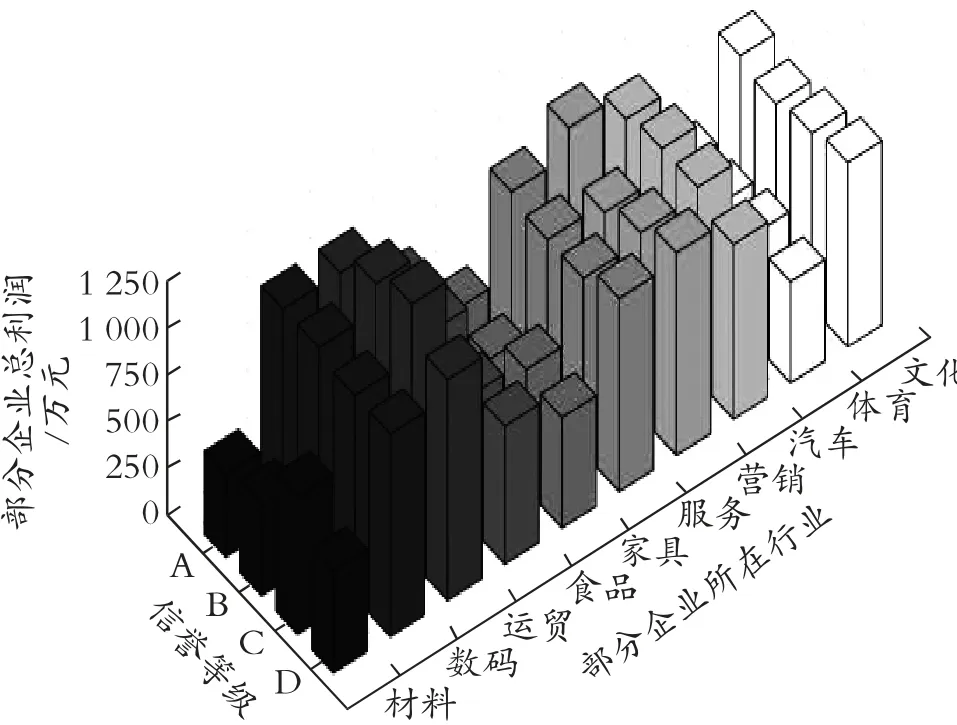
图2 企业信誉与营业额的三维柱状图
3 研究模型的建立
3.1 莫楞贝算法改进遗传算法优化SVM 的参数
SVM 分类器中的参数是本文信誉等级评价模型的关键,包括惩罚参数和核函数参数,因此,在利用SVM 进行信誉等级评价时需要在训练数据之前对SVM 的参数进行优化[1],具体步骤如下。
步骤1:编码参数δ 和c,生成初始种群,即

步骤2:选择双亲交叉运算,若交叉结束后得到的个体优于亲本,则进行替换,当交叉的个体数大于种群数量的50%后,则结束交叉。
步骤3:选择个体进行变异运算,突变参数如下式所示,若变异结束后得到的个体优于亲本,则进行替换,当变异的个体数大于种群数量的50%后,则结束交叉。
设m 为要突变的参数,m'i为莫楞贝突变的结果参数,突变公式为
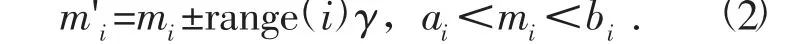
式中:range(i)为突变范围,通常为0.1(bi-ai),突变范围的正负误差不超过0.5;αk∈{0,1},P(αk=1)=1/16。
步骤4:进化完成后,如果达到迭代数则结束运行并将个体进行解码,得到最优参数组合δ 和c的值。
3.2 基于MGA-SVM 算法的信誉等级评价模型
步骤1:将123 家有信贷记录的企业信息导入,并进行数据归一化,其中80 家企业为训练样本,剩余43 家企业为测试集。
步骤2:训练SVM 诊断模型,选用RBF 核函数,且利用模型准备中优化好的参数组合。
步骤3:仿真测试。
步骤4:得到302 家企业的信誉评价等级。
3.3 基于AHP-模糊数学方法的信贷风险评价量化模型
3.3.1 确定指标体系
在分析信贷风险问题时,将可能的影响因素划分为目标层A、准则层B、指标层C 3 个层次。其中,目标层为银行信贷风险水平A;准则层为盈利状况B1、成长状况B2、信誉状况B3;指标层为利润率C1、有效交易率C2、净利润增长率C3[2-3],具体模型指标体系,见图3。
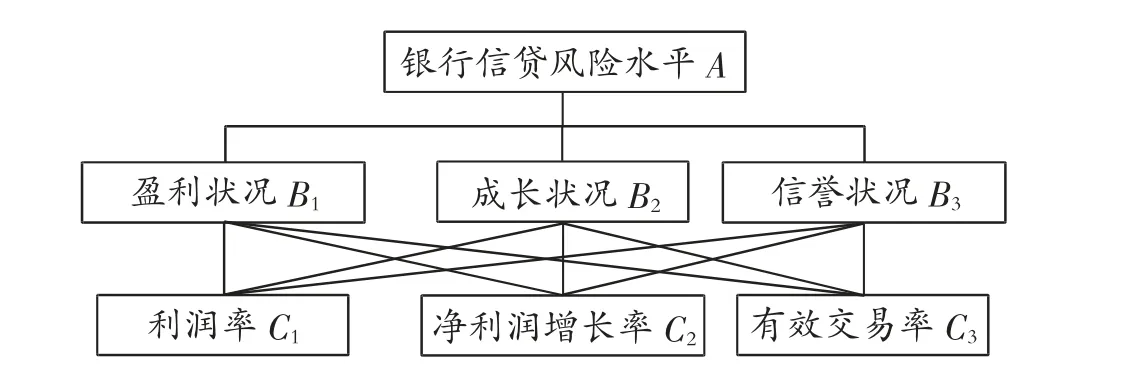
图3 模型指标体系
3.3.2 构造判断矩阵
判断矩阵是用来衡量目标层、准则层、指标层中两个影响因素之间的相对重要程度。
根据各个因素相对重要程度的不同,本文采取分的比例进行赋值,具体比例标度值,见表2。
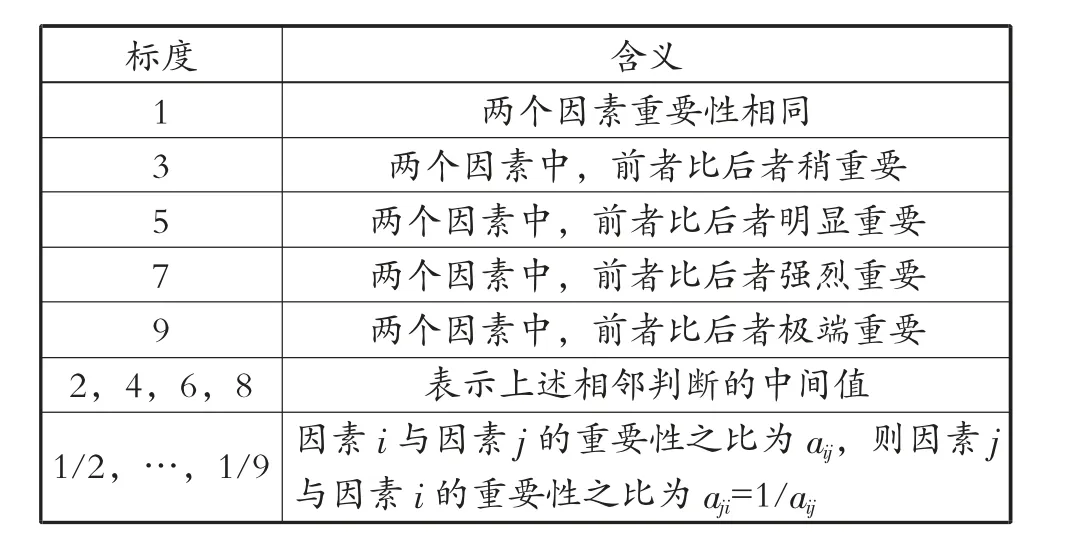
表2 比例标度值
由此可得判断矩阵P,见表3。
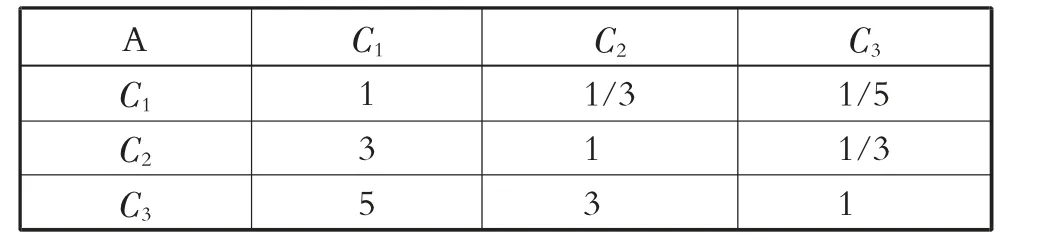
表3 判断矩阵P
3.3.3 一致性检验
本文认为人为判断影响信贷因素的相对重要性具有一定的主观性。因此,为了避免在对多个因素进行判断时出现前后不一致的现象,需要进行一致性检验。
其中,一致性矩阵R 具有各行(列) 间成倍数关系的特征,则有
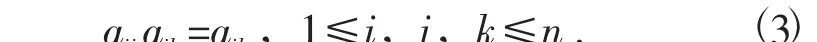
计算一致性指标CI 为
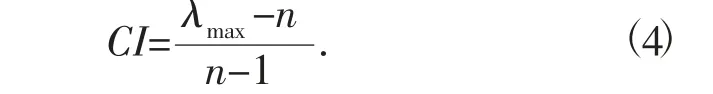
式中:λ 为一致性矩阵的最大特征根;n 为一致性矩阵的阶数。可查找对应的随机一致性指标RI,见表4。

表4 随机一致性指标
计算一致性比例CR 为

若CR<0.1,则判断矩阵的一致性可接受;若CR>0.1,则需要对判断矩阵进行修正。本题求得判断矩阵CR=0.034 5<0.1,说明该矩阵通过一致性检验。
3.3.4 计算权重
本文采用算术平均法求解权重,具体计算步骤如下。
步骤1:将判断矩阵按列归一化(每个元素除以所在列的和),表达式为

最后计算权重向量。
3.3.5 确定模糊综合评判模型
建立评语集U={u1,u2,u3,…,un},其中影响因素uj代表第j 种评价结果。本文对银行信贷风险的评价分为“无风险” (u1)、“轻微风险” (u2)、“一般风险” (u3)、“较大风险” (u4)、“大风险”(u5) 5 个等级,即确定的评语集为U={u1,u2,u3,u4,u5,u6}。
建立模糊关系矩阵Q 为

式中:qij表示各个企业ui从单因素来看对评价集U的隶属度。
因此,各指标得分情况的计算公式为

式中:Di表示第i 个指标的得分,当Di达到最大时,其所对应的等级可作为综合评判结果ui,此时Di的最大值为该企业的风险系数Fi。
综上所述,基于AHP-模糊数学方法的信贷风险评价量化模型为
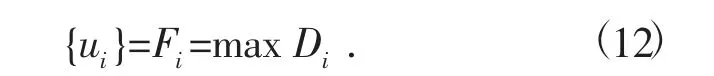
3.4 基于风险系数占比的贷款额度模型
令AHP-模糊数学方法的信贷风险评价模型中每家企业最大指标得分Di为银行信贷的风险系数Fi,因此,风险系数与利润率、有效交易率、净利润增长率有关。为使放贷风险尽可能小,本文选择对“无风险”“轻微风险”“一般风险”的企业进行放贷。为了减少企业贷款的差别化,本文选取占比法对放贷额度进行计算。
综上所述,基于风险系数占比的贷款额度模型表达式为
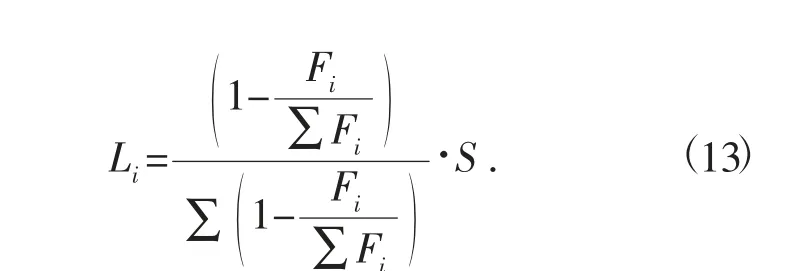
式中:Li为贷款额度;Fi为风险系数;S 为银行年度放贷总额度。
3.5 基于PLS 方法的贷款利率最优决策模型

步骤1:数据标准化。


同理,可将hij转化成标准化指标值~hij。
步骤2:求相关系数矩阵。
步骤3:分别提取自变量组和因变量组的成分。
步骤4:求两个成分对时标准化指标变量与成分变量之间的回归方程。
步骤5:回归方程的确立。求因变量组和自变量组之间的回归方程,也就是基于PLS 方法的贷款利率最优决策模型的回归方程,即
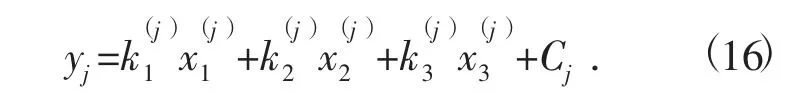
式中:C 为常数。
步骤6:约束条件的确立。
为了保证银行放出的贷款能够最大可能地收回,需要约束企业年利润总额大于100 000 元,即

为了将银行信贷的风险降到最低,贷款利率最优决策模型对企业的成长能力也有一定的要求,规定企业的有效交易率大于95%,即

为了稳定银行信贷的客户量,本文规定客户流失率不得超过50%,即

综上所述,基于PLS 方法的贷款利率最优决策模型为
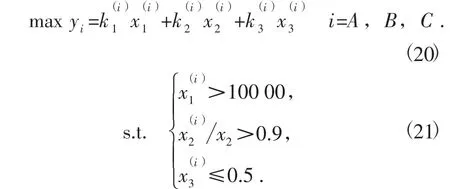
4 模型的求解
基于粒子群算法求解模型如下。
步骤1:PSO 算法参数设置。
对于贷款利率最优决策模型当中,PSO 算法中的每一个粒子代表一个贷款利率的潜在解,每个贷款利率潜在解粒子由位置、速度和适应度3 个指标表征[5]。在进入算法前需要对参数进行设置。其中,c1=1.494 450,c2=1.495 545,genmax=300,popmax=2,popmin=-2,sizepop=20,νmax=0.5,νmin=-0.5。
步骤2:粒子适应度计算。
所有的粒子都由一个fitness-function 函数确定适应值以判断目前位置的好坏。
步骤3:寻找初始极值。
根据初始粒子适应度寻找个体极值和群体极值。
步骤4:迭代寻优。
每个贷款利率潜在解粒子具有记忆功能,及时更新自己的速度和位置,并且能记住所搜寻到的最佳位置。
最终得到302 家企业的信誉评级情况,见表5。
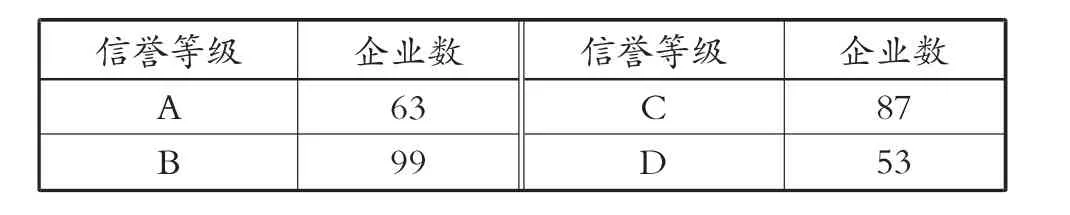
表5 302 家企业的信誉评级情况
将以上企业信誉评级情况代入AHP-模糊数学方法的信贷风险评价模型,除53 家信誉等级为D的企业外,剩余249 家企业信贷风险等级见表6。
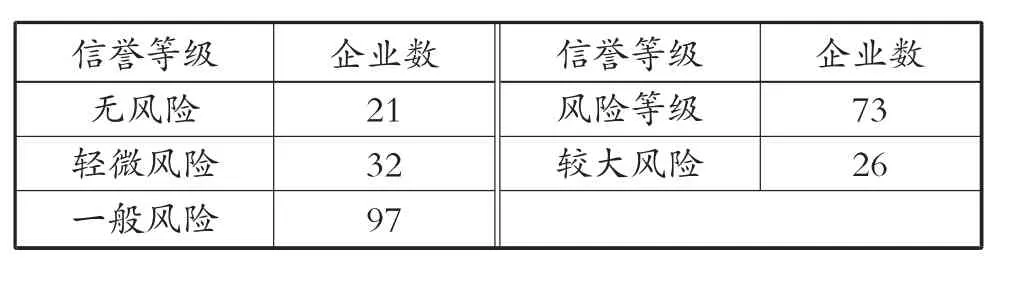
表6 249 家无信贷纪录企业的信贷风险等级
选取“无风险”“轻微风险”“一般风险”的企业代入基于PLS 方法的贷款利率最优决策模型得到模型回归方程,即

信用等级为A 的企业银行给予的贷款利率最优为0.046 5,信用等级为B 的企业银行给予的贷款利率最优为0.050 5,信用等级为C 的企业银行给予的贷款利率最优为0.058 5。
通过问题求解银行信贷策略,见第51 页表7。
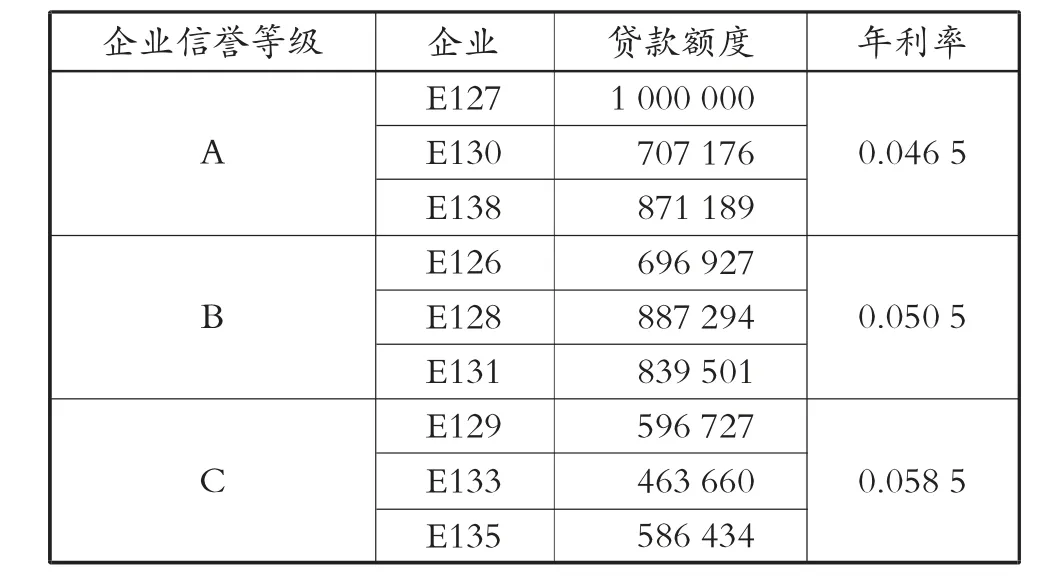
表7 部分信贷策略表
5 模型的检验
5.1 基于PLS 方法的贷款利率最优决策模型的检验
为了更直观迅速地观察各影响因素自变量在解释贷款年利率时的边际作用,对标准化数据的回归方程绘制回归系数图(以问题一为例),见图4。
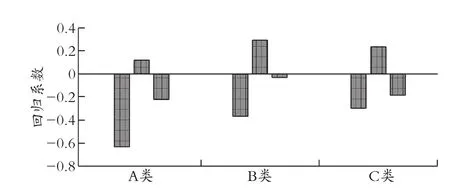
图4 回归系数图
从回归系数图中可以观察到,每年利润总额在解释3 个回归方程时起到了极为重要的作用。然而,与信誉等级为A 级和B 级相比,C 级的每年利润总额对回归方程的解释较差,但误差仍在允许范围内,证明了本文模型的合理性。
5.2 基于MGA-SVM 算法的信誉等级评价模型的检验
对80 家训练样本企业和43 家测试样本企业进行测试,测试结果见图5。图中显示预测正确率将达到93.256 1%,由此可见本模型的正确率较高。
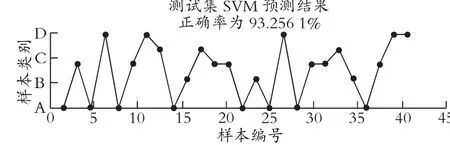
图5 测试集SVM 测试结果对比
在保证其他参数不变的情况下,仅仅修改核函数的类型,选择不同核函数时的训练集和测试集预测正确率,见表8。
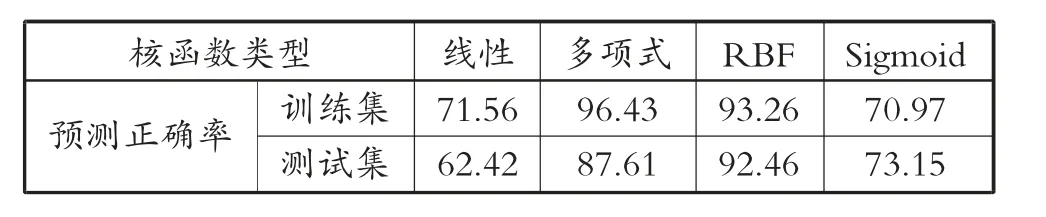
表8 不同核函数集合正确率 (%)
由表8 可见,训练集中多项式的正确率最高,但其测试率较低,线性和Sigmoid 在训练集和测试集当中的正确率均不够理想。因此应选择RBF 核函数,本文证明了该模型的合理性和准确性。
6 结束语
本文中基于AHP-模糊数学方法的信贷风险评价模型,把定性核定量分析有机结合成较好的科学决策方法。此外,基于MGA-SVM 算法的信誉等级评价模型采用了莫楞贝算法优化遗传算法对SVM的参数进行优化,减少了迭代次数和所用时间,有效增强了SVM 的分类识别性能。本文对中小微企业信贷决策的研究能够降低银行的信贷风险,为银行提供最佳的放贷策略。

