盘活素材 触摸数学本质——《线的整理与复习》教学微探

文|简海荣

【教学内容】

北师大版四年级上册。

【教学过程】

一、思考引领，开启认知

师：同学们，数学是需要我们去发现、探索的，来看微视频（播放微视频），你发现了什么？

生：点动成线，线动成面，面动成体。

师：是的，图形的世界里有点、线、面、体，今天我们一起进行有关线的整理与复习，让我们带着下面的思考开始本节课的复习：

1.通过复习你更清楚了哪些问题？清楚了什么？

2.什么题目让你有了新的思考角度和方法？

3.解决哪个问题时，纠正了你原来怎样的错误认识或找到了哪些出错的原因？

【设计意图：开课初，借助“三点思考”进行课前慎思，帮助学生开启良好的认知意识，引领学生学习及思考的方向。】

二、脉络梳理，整合提升

1.梳理知识，在交流补充中完善线的认知。

师：课前，同学们已经对线的知识进行了初次梳理，谁来与大家分享一下？

（学生汇报，互相补充）

师：通过自己课前的初次梳理和交流，大家对线的认识和关系进一步明确。那接下来请同学们拿出学具袋里的材料，以小组为单位，摆一摆，对这些内容进行梳理。同时，老师还准备了空白贴，如果你还有其他的补充，就写出来。先来看活动要求：

思：思考怎么分类？

摆：在动手操作中完成知识梳理。

议：活动中你的困惑是什么？

（学生小组活动，交流小组活动中的困惑）

生：为什么垂直是相交的特殊情况？如何理解特殊？

师：（课件动态演示）首先，它们都有一个交点，两条直线在相交时会产生锐角、钝角、直角，当相交成为直角时，就说两条直线相互垂直，所以说垂直是相交的特殊情况。

师：既然困惑已经解决了，那现在请大家进行最后的调整，并进行粘贴和连线。

总结：刚才的讨论和补充让梳理更具条理性，认知也更全面。活动中，先进行了内容整理，再在补充梳理中形成知识脉络，这样的复习方法不仅可以用在数学的单元复习中，也可以在其他学科中学习使用。

【设计意图：通过课前梳理及课上回顾交流，以聚焦的方式再次帮助学生深化关于线的认知。同时，对于本单元中学生还可能存在的困惑点进行了细致解读，帮助学生建立正确清晰的认知，既充分沟通了知识之间的联系，又培养了学生归纳梳理的能力。】

2.着眼生活，在思辨中发展数学应用意识。

师：接下来我们在生活中体会线的应用。在这扇窗户里，你能发现哪些线的位置关系？

生：平行、垂直。

师：请说具体一些，哪两条线互相平行？哪两条线互相垂直？

生：窗户上面的横向窗框与下面的横向窗框互相平行。

生：窗户的横向窗框与竖向窗框互相垂直。

师：看着像平行就是一定是平行关系吗？

生：测量两条横向窗框之间的距离，如果这些距离都相等，则这两条窗框就是平行的关系。

师：慧眼识真理！工人师傅们在制作窗框时，中间这些竖向窗框的长短就是相等的，用数学语言来说就是：平行线之间的距离处处相等。之前，我们在画平行线的过程中，也隐藏了这样的道理，来看视频。（视频播放利用一副三角板画平行线的动态过程）

师：平行和垂直在生活中的应用是很广泛的，只要同学们用心观察，就能发现更多这样的现象。（课件出示西安-安康的路线图）

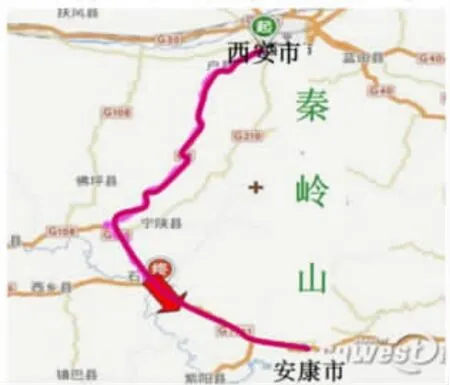
师：安康是西安的后花园，在前几年，人们去安康需要长途绕行，很不方便，如果你是设计师，你有什么想法？

生：从西安修一条到达安康的直直的路线，因为两点之间线段最短。

师：金点子，为你点赞！的确如此，后来，人们经过开山、凿洞、架桥，打通秦岭山，修建了西安到安康这条方便快捷的高速路。同样的道理，还体现在港珠澳大桥的设计上。

（音频资料：港珠澳大桥是粤港澳三地首次合作共建的超大型跨海通道。没有这座大桥之前，珠海、澳门与香港之间的陆上交通需要3 个多小时。设计师们利用两点之间线段最短的原理，克服万难，经过6年的前期准备、9年的艰苦建设，修建了港珠澳大桥，并于2018年10月24日正式开通。自此，港珠澳大桥在推动粤港澳三地社会经济可持续发展的同时，也必将发挥强信心、聚共识的作用）

师：既然两点之间线段最短，可为什么无论是西康线还是港珠澳大桥，都设计成这样了呢？

（课件出示西康线以及港珠澳大桥的俯瞰图，有弯曲现象）

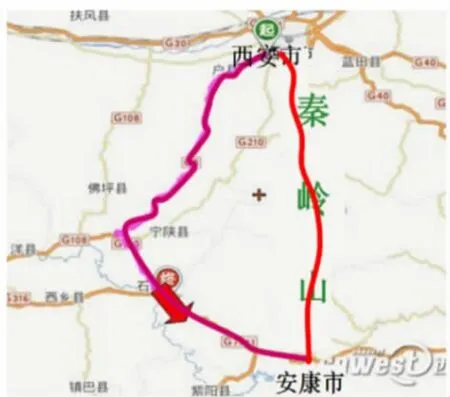
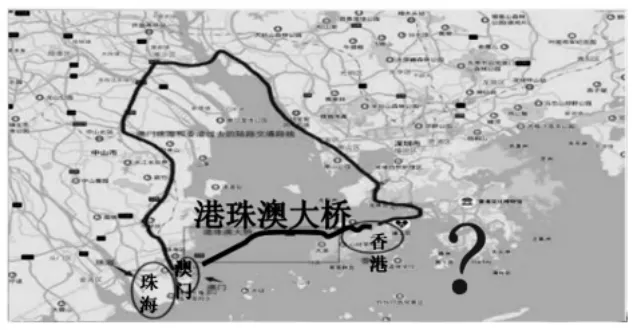
生：实际建设中会受到地理环境等客观因素的影响。

师：是的，数学服务于生活的同时，还要考虑到地理环境等客观因素的各种影响，尽管条件艰苦，工程师们还是最大限度的应用了两点之间线段最短的原理进行设计，同时也成就了它的几个世界之最：世界第一长的跨海大桥，世界第一长的海底沉管隧道，世界第一深的沉管隧道。正是这诸多的世界之最，也使得港珠澳大桥被誉为“新世界七大奇迹”之一。此情此景下，你有什么感想？

生：中国人民很厉害。

生：知识的力量是无穷大的。

师：大家的民族自豪感也油然而生。

【设计意图：借助“西康线”“港珠澳大桥”等具有时代感的生活案例，引导学生理解数学服务于生活，但并非是精准应用于生活，因为在生活应用中我们还要考虑到各种客观因素带来的影响。让学生从生活中的多个角度出发，感受社会生活对数学知识的需求，也让学生对于数学的应用意识从身边的小认识走向社会建设及发展的大认识，积极地发展了学生的数学应用意识。】

三、内部关联，感悟本质

师：近几年来，社会的发展促进了内地与香港更多的交流，人们也常常乘坐高铁从广州出发去香港，来看一看，这个问题该怎么解决？（课件出示广州-香港的高铁路线图）

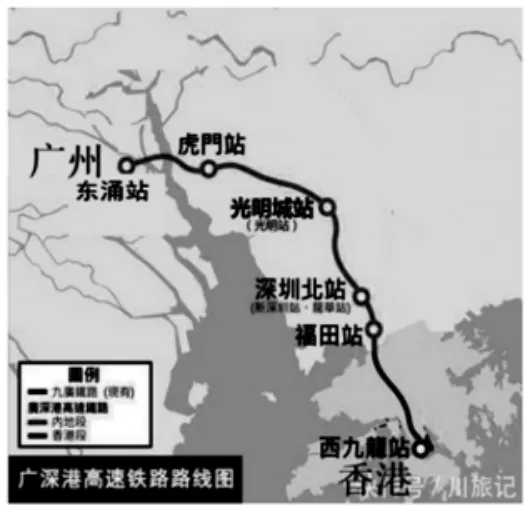
出示：如图，从广州东涌站到香港的高铁，有多少种不同的票价？

生：15 种。列式为5+4+3+2+1=15（种）。

师：说说你是如何得到的。

生：我是排队数，从每一个站点出发，看看这个站点到其他站点有几种情况，最后再求和。

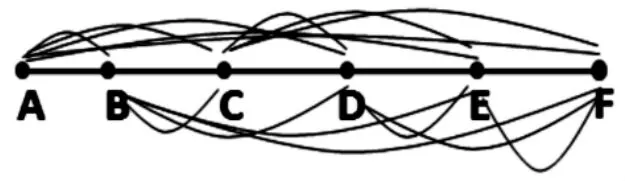
生：我是分类数，先看每相邻两个站点之间有5 种情况，然后再两段、三段、四段、五段拼接起来数，最后再求和。

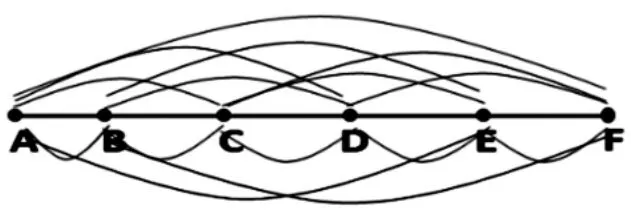
师：同学们很厉害，用不同的方法解读了同一个算式。我想问，在刚才的不同数法中，除了算式相同之外，还有什么是相同的？

生：有序思考。

师：是的，能够让我们做到不重复、不遗漏的数。那大家有没有觉得这样的思考方法以及算式在我们日常学习中的出场率很高呢？

师：考考你，老师这里也有一个问题是用算式“5+4+3+2+1”来解决的，猜猜看，它能解决哪些数学问题呢？

生：数长方形共有多少个的问题。

生：能解决一共有几个角的问题。

生：能求出6 个人握手的总次数。

生：能解决6 个球队的循环赛问题。

生：能解决6 个站的单程车票问题。

师：还可以是求6 条直线最多有几个交点的问题；求6 个三角形点阵点数总和的问题等等。用5+4+3+2+1 解决像这样的图形规律问题，在五、六年级的学习中我们会了解更多，同学们可以在后续学习中继续研究。

总结：看来知识之间都是相通的，这些问题看似不同，却都有着相同的思考方式和解决方法。

师：关于今天的生活体会，你有什么想说的吗？

生：数学的应用非常广泛，能帮助我们解决很多生活中的问题。

师：是的，生活中的万事万物都蕴藏着丰富的数学知识，正像华罗庚先生所说，“宇宙之大，粒子之微，火箭之速，化工之巧，地球之变，生物之谜，日用之繁，无处不用数学。”

师：华罗庚先生还说，数学是一切科学的得力助手和工具。所以，学好数学，就是增强自身解决问题的能力。

【设计意图：复习有新意，思绪在延伸。本环节是思想方法认知的暗线。通过解决问题时的有序思考，让学生感受到有序思想的应用可以让我们的学习更有条理、更为清晰，也明白了知识之间都是互相关联的，有些问题看似不同，却都有着相同的思考方式和解决方法，发展了学生透过表层看本质的分析问题的能力，也让学生感受到了数学学习的奥妙。】

四、反思回顾，提升能力

师：按照课前的约定，请同学们说说在本节课的学习中，你的认识发生了哪些变化，又有了哪些新的收获和体会。

总结：正所谓千金难买回头看，每一次回头都是一次新的探索。在今天的复习中，我们带着新的眼光分析了熟悉的内容，又产生了很多新的感悟，也再次从中也体会到了本单元学习的价值。

【设计意图：在课的结尾处，让学生通过反嚼来进行梳理、交流，有助于学生对整节课的内容进行消化与吸收，尤其是通过复习产生的新的认知和感悟，对发展学生的数学应用意识的帮助是比较大的。】

（“第十三届小学教学特色设计大赛”获奖作品选登）