化静为动 动中思变 变中求联——《数对的变化特征》教学

文|朱曙光 高鹏飞

【教学内容】

人教版五年级上册“用数对表示物体位置”的拓展。

【课前慎思】

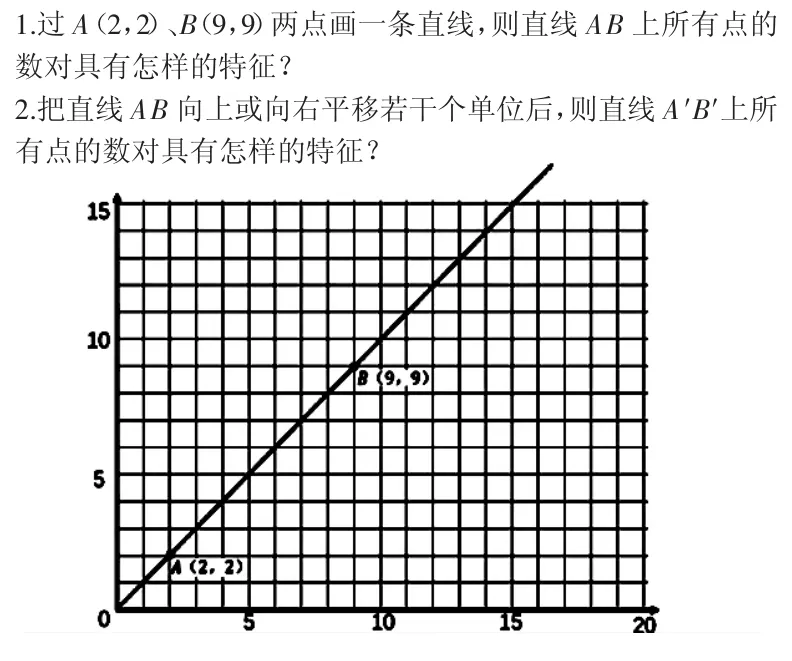
在一次练习参阅时，发现下图的题目很有研究价值，既可以作为“位置”单元的复习，又可以用来拓展“数对”的知识。该题目体现了“解决问题教学重要的是基于学习材料，挖掘学习线索，引导学生经历探索、解决、拓展的问题研究全过程，帮助他们建构完整的知识脉络，促进数学知识的理解走向通透和高阶思维的系统发展。”的意蕴。让学生发现数对的变化特征，能用符号表示一条直线上数对的关系，感悟函数思想是本课的要点。基于此，笔者进行了尝试。

【课中深思】

一、前置反馈，初步感知

师：课前，我们一起完成了“数对”的前置性作业，请同学们来说一说你们的想法。（出示部分学生的作业）

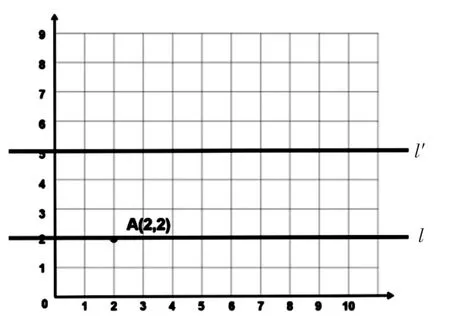
生：第一题：直线l 上的点可以用（1，2）（2，2）（3，2）等数对来表示，我发现这些点都在第2 行，列不确定。所以这些点可以用数对（a，2）来表示。

生：第二题：直线l′上的点可以用（1，5）（2，5）（3，5）等数对来表示，我发现这些点都在第5 行，列不确定。所以这些点可以用数对（a，5）来表示。

生：直线l 向上平移3 格，对应点列不变，行加3。

生：这些直线上的点都是行一定，列不定。

【设计意图：从简单的水平直线入手，复习用数对表示点的位置，并经过向上平移3 格来体会列不变、行加3 的规律。并能在行一定时，会用（a，2）（a，5）等数对表示平移前和平移后直线上的所有点。】

二、迁移类推，横纵对比

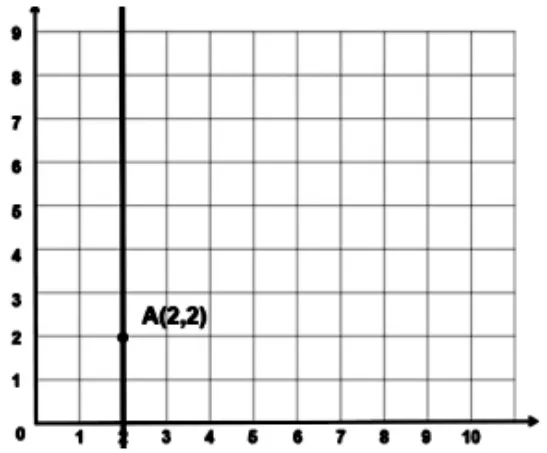
师：如果将直线l 绕点A（2，2）旋转90°，那么新直线的点怎么用一个数对来表示？

生：这条直线上的点都在第2 列，行不确定，用数对（2，a）来表示。

师：如果将这条直线向右平移3 格呢？

生：列加3，用数对（5，a）表示。

生：不管向左还是向右平移，这些直线上点的列一定，行不定。

师：与水平方向的直线相比，这些直线有什么不同？

生：水平方向直线上的点行一定，列不定；竖纵方向直线上的点列一定，行不定。

【设计意图：从水平方向的直线延伸到竖纵方向的直线，并经过向右平移3 格来体会行不定、列加3的规律，不管向左还是向右平移，竖纵方向直线上的点列一定，可用（2，a）（5，a）等数对表示，为后续学习做铺垫。】

三、动态变换，变中求联

1.一“转”，用数对表示点的规律。

师：再把直线绕点（2，2）顺时针旋转45°，这条直线上的点还能用数对表示吗？

生：（1，1）（2，2）（3，3）……

生：这些点所表示数对的行和列都相等，用（a，a）表示。

生：如果这个点在第a 行，那么一定也在第a 列。

【设计意图：找点，标数对，并研究数对的特征，锻炼学生的观察、归纳能力。用一个数对表示所有点，对学生提出了更高的概括要求，促进学生的思考。】

2.二“升”，用数对表示线的变化。

师：如果把这条直线向上平移3 格，你打算怎么画？

（学生汇报，教师将学生的反馈汇总入表格）

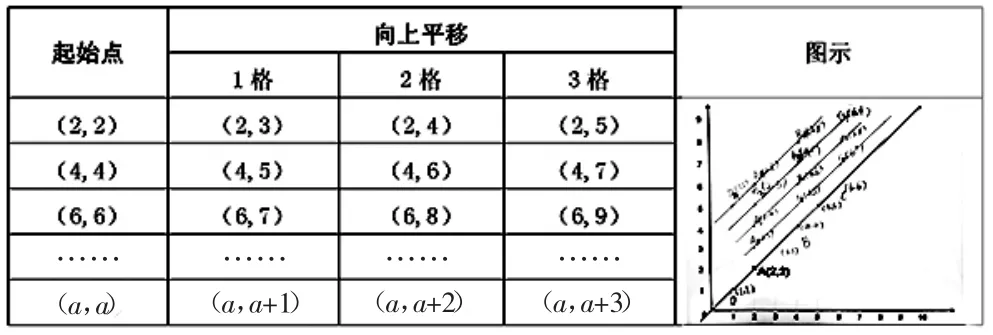
images/BZ_52_1286_330_2267_654.png

师：观察表格，你发现了什么？

生：将直线向上平移几格，对应点的行就加几，但列不变。

师：原因是什么？

生：因为直线只向上平移，所以列不变，行增加。

师：如果向上平移n 格呢？

生：列不变，行加n，这条直线上的点可以用数对（a，a+n）表示。

【设计意图：通过画图指导，突破难点。先由学生自主确定向上平移的格数，再确定任意两点向上平移后的位置，由这两点确定一条直线。最后，标出三个点平移前、后的数对，观察变化，找到规律。】

3.三“移”，整体感知数对的变化。

师：我们通过小组合作发现一条直线向上平移后相应点的变化规律，如果把这条直线向下、向左、向右平移，又会有什么规律呢？我们来大胆猜想一下。（根据学生的回答板书）

师：是否果真如此，让我们一起来验证吧。算一算，填一填，画一画。

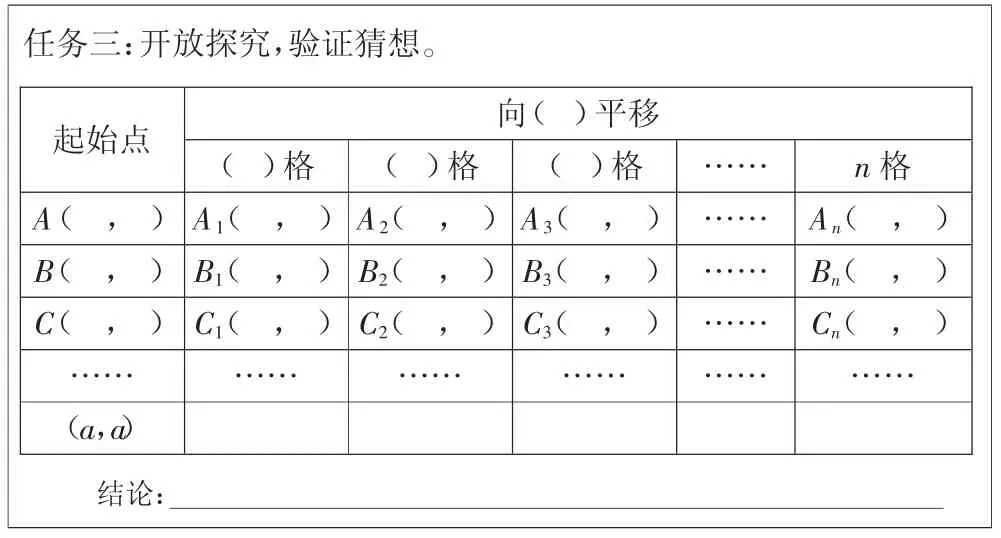
任务三：开放探究，验证猜想。起始点 向（ ）平移（ ）格 （ ）格 （ ）格 …… n 格A（ ，）A1（ ，）A2（ ，）A3（ ，）…… An（ ，）B（ ，）B1（ ，）B2（ ，）B3（ ，）…… Bn（ ，）C（ ，）C1（ ，）C2（ ，）C3（ ，）…… Cn（ ，）…… …… …… …… …… ……（a，a）结论：

生：我们组研究的是直线向下平移，起始点是A（4，4）、B（5，5）、C（6，6），在平移的过程中列不变，行变化：向下平移1 格，行减1；向下平移2 格，行减2；向下平移3 格，行减3……向下平移n 格，行减n。

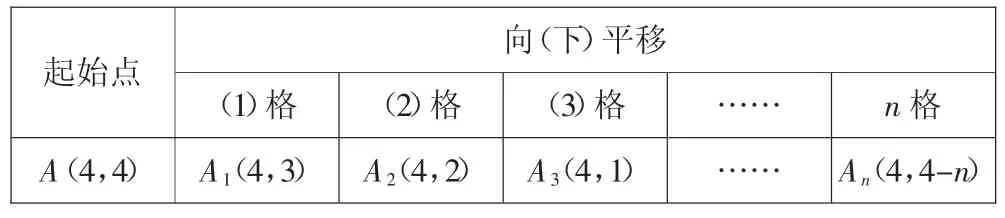
起始点向（下）平移（1）格 （2）格 （3）格 …… n 格A（4，4）A1（4，3）A2（4，2）A3（4，1）…… An（4，4-n）

B（5，5）B1（5，4）B2（5，3）B3（5，2）…… Bn（5，5-n）C（6，6）C1（6，5）C2（6，4）C3（6，3）…… Cn（6，6-n）…… …… …… …… …… ……（a，a）（a，a-1）（a，a-2）（a，a-3）…… （a，a-n）

生：我们组研究的是直线向左平移，起始点是A（5，5）、B（7，7）、C（9，9），在平移的过程中行不变，列变化：向左平移1 格，列减1；向左平移2 格，列减2；向左平移3 格，列减3……向左平移n 格，列减n。

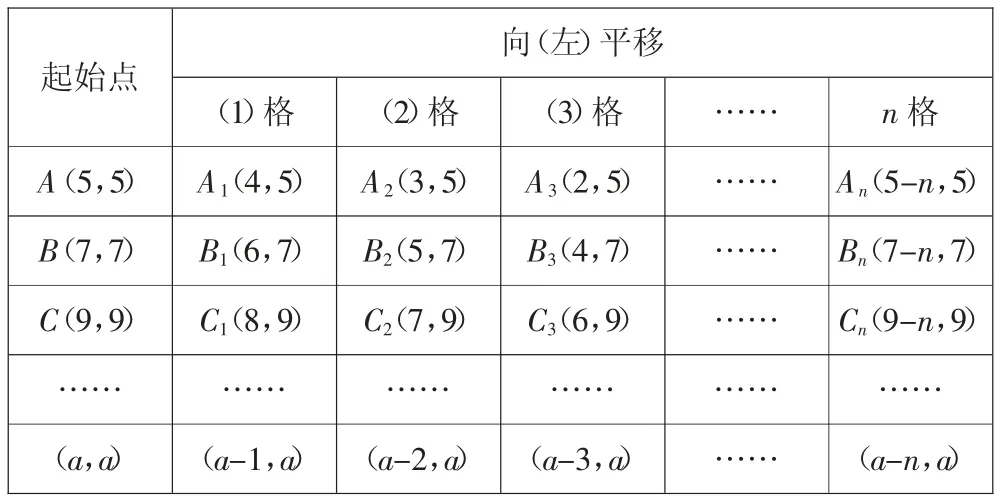
向（左）平移（1）格 （2）格 （3）格 …… n 格A（5，5）A1（4，5）A2（3，5）A3（2，5）…… An（5-n，5）B（7，7）B1（6，7）B2（5，7）B3（4，7）…… Bn（7-n，7）C（9，9）C1（8，9）C2（7，9）C3（6，9）…… Cn（9-n，9）…… …… …… …… …… ……（a，a）（a-1，a）（a-2，a）（a-3，a）…… （a-n，a）起始点

生：我们组研究的是直线向右平移，起始点是A（1，1）、B（2，2）、C（3，3），在平移的过程中行不变，列变化，向右平移1 格，列加1；向右平移2 格，列加2；向右平移3 格，列加3……向右平移n 格，列加n。

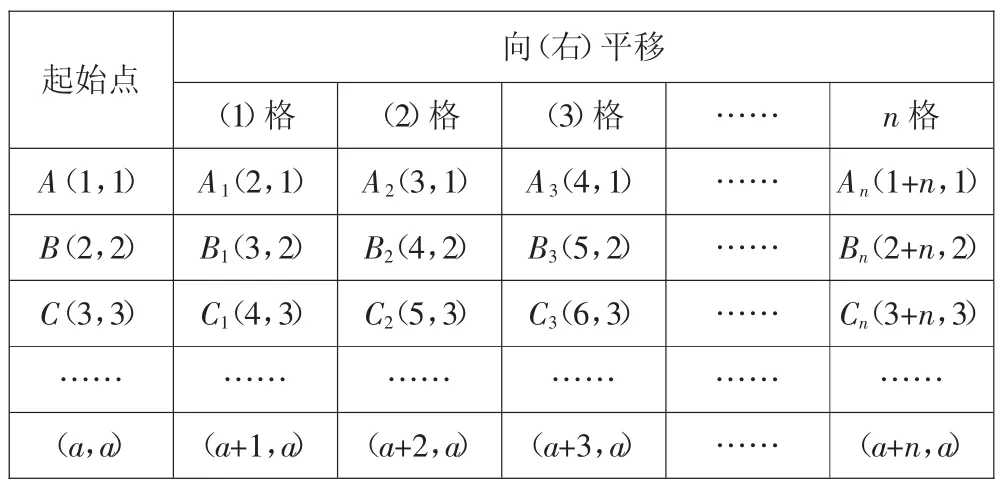
向（右）平移（1）格 （2）格 （3）格 …… n 格A（1，1）A1（2，1）A2（3，1）A3（4，1）…… An（1+n，1）B（2，2）B1（3，2）B2（4，2）B3（5，2）…… Bn（2+n，2）C（3，3）C1（4，3）C2（5，3）C3（6，3）…… Cn（3+n，3）…… …… …… …… …… ……（a，a）（a+1，a）（a+2，a）（a+3，a）…… （a+n，a）起始点

小结：大家的分享都很优秀，如果直线向上或向下平移n 格，相对应点的列不变，行对应加n 或减n；如果直线向左或向右平移n 格，相对应点的行不变，列对应减n 或加n。

师：如果一个点是（1，1），向左平移3 格后的对应点是？向下平移3 格后呢？

生：向左平移3 格是（-2，1），向下平移3 格是（1，-2），但画不了。

【设计意图：在完成任务二的基础上，提出更加开放的研究任务。学生自主选择向下、向左或向右平移，经历猜想、验证、结论的过程。汇报时，在不同组呈现不同方向平移的研究过程中，教师适时提出原数对格子图不够用，可以向左和向下拓展，就由第一象限拓展到第二、三、四象限，为后续的学习奠定了基础。】

四、基于拓展，文化渗透

师：如果把直线向下平移5 格，你能说出点（2，2）所对应的点的位置吗？如果向左平移5 格呢？

生：是（2，-3）和（-3，2）。

师：想象一下，这两个点分别在哪里？你能用一个数对表示它们所在直线上的所有点吗？

生：在这个数对图的下面和左面。（如下图）

生：（a，a－5）和（a－5，a）。

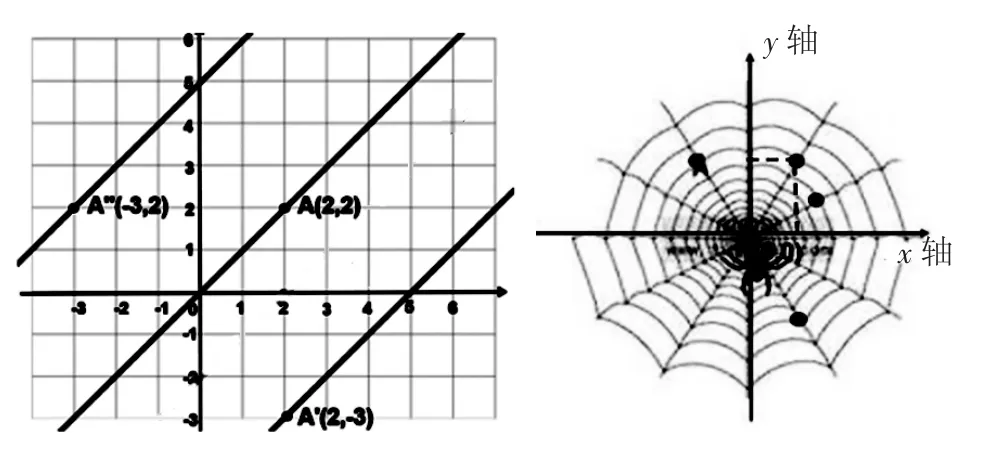
师：看来数对所表示的点不仅仅在这个区域，它还可以在这、在这……我们的这个发现和著名数学家笛卡尔是一样的，他当时就是从一个蜘蛛网想到了这个问题。（课件出示下图）所以，数学来源于生活，关于数对的知识还有很多，我们以后会继续研究。

【设计意图：从第一象限拓展到第二、三、四象限，便于和之后学习“平面直角坐标系”的知识相衔接。】

五、回顾总结，反思提升

1.全课总结：说一说，这节课我们学习了什么？我们是怎么进行研究的？

（通过全课总结，形成板书）

2.课外探究：在坐标上任意画一条直线，用一个数对表示线上的点；将直线上、下、左、右平移若干个单位后，这些点有什么变化？

【设计意图：通过回顾与总结，提炼出从特殊到一般的数学学习方法；对所学知识进行建构，加深印象，促进理解内化，同时也是对学生反思能力的提升；将探究延伸到课后，研究其他的直线，拓展思维。】