Prediction of scandium tetraboride from first-principles calculations:Crystal structures,phase stability,mechanical properties,and hardness*

Bin-Hua Chu(初斌华) and Yuan Zhao(赵元)

School of Physics and Opto-Electronic Engineering,Ludong University,Yantai 264025,China

Keywords: first-principles calculations,high pressure,transition metal borides

1. Introduction

Superhard materials are broadly useful in scientific research and industrial applications such as cutting instruments and hard coating,due to their superior properties in high thermal conduction,chemical stability,and high strength. The superhard materials usually exist in those strongly bonded materials formed by light elements,such as diamond,c-BN,B6O,BC5,and BC2N.[1-7]These compounds typically have a high density of electrons and strong covalent bonds. Unfortunately,these compounds are rare and expensive, which can only be produced under extremely high-pressure and high-temperature environments. Several attempts have been made to develop new hard materials. Recent evidence suggests that the incorporation of boride, carbide, nitride, and oxide into heavy transition metals (TMs) is a strong candidate for the design of modern hard materials, such as ReB2, OsB2, RuO2, and WB4.[8-12]The incorporation of light elements increases the stability of the transition metal by forming a strong covalent linkage between the TM and the light elements. These compounds have been successfully synthesized under ambient or high pressure,and they usually have large bulk and shear moduli. These groundbreaking studies, therefore, open up a new avenue for producing superhard materials.

Recent work has established that 3d-series transition metal tetraborides usually have an unusual three-dimensional framework of interconnected rhombic B4units. In these compounds,CrB4with a hardness of 48 GPa under environmental pressure conditions was confirmed to be superhard.[13]MnB4has a high mechanical performance,with the Vickers hardness to be as high as 40.1 GPa.[14]Besides, Gouet al.reported the successful synthesis of FeB4experimentally.[15]In this study, FeB4was said to have a hardness of up to 62(5) GPa.In a subsequent study, in various analytical models, Zhanget al.have stated that FeB4’s Vickers hardness is between 11.7 and 32.3 GPa.[16]Therefore, 3d-series transition metal tetraborides are considered as one of the ideal materials for the design and synthesis of novel superhard materials. In the Sc-B systems,ScB2,ScB12,ScB15,and ScB19have been studied in experiments.[17-20]Among them, ScB2takes the hexagonal structure (No. 191,P6/mmm). For ScB12, cubic structure (No. 225,Fm-3m) and tetragonal structure (No. 139,I4/mmm) have been studied. The crystal structure of ScB15belongs to the tetragonal structure (No. 76,P41). Besides,ScB19belongs to the tetragonal structure(P41212 orP43212).In 2019,Baiet al.published a paper in which they described that ScB3is a monoclinicC2/mstructure with a hardness of 37.1 GPa.[21]However,there are no theoretical or experimental reports on ScB4up to now. To our knowledge, the determination of crystal structure is essential for understanding its physical properties. ScB4’s uncertainty of the ground state and high-pressure phases contributes to the presence of exotic physical actions. Therefore, resolving the crystal structure of ScB4at ambient conditions and high pressure has an important significance.

In this study,the crystal structures,mechanical,and electronic properties of ScB4are systematically explored within a wide range of conditions(0-100 GPa)by using first-principles calculations on crystal structure prediction. An orthorhombicCmcmphase has been uncovered for ScB4.TheCmcmphase is much more stable energetically than the previously proposed CrB4-, FeB4-, MnB4-, and ReP4-type structures at ambient pressure. But at high pressure, thePnmaphase is more stable. Then the structural property,structural stability,mechanical,dynamic,and electronic properties for the new phases are studied by first-principles.

2. Computational detail

In this work, we use the developed crystal structure prediction method by the CALYPSO to search the potential crystal structures of ScB4at ambient pressure.[22-24]The structure relaxation is performed in the Viennaab initiosimulation package (VASP) code.[25-27]The exchange-correlation functional is treated by the generalized gradient approximation (GGA) with the projector-augmented wave (PAW)potential.[28,29]The 2s22p1and 3p63d14s2are separately selected as the valence electrons for the B and Sc atoms. Thek-point samplings in the Brillouin zone are performed using the Monkhorst-Pack scheme with a grid density of 0.03×2π˚A-1employed in the Brillouin zone integration. The formation enthalpy of ScmBnis determined by the equation ΔH=H(ScmBn)-mH(Sc)-nH(B), where the Sc element from its hexagonal phase andα-B (0-19 GPa),γ-B (19-89 GPa),andα-Ga phase (89-100 GPa) are used to be the referenced phases.[30]The phonon spectra are carried out by drawing the supercell approach as performed in the PHONOPY software package.[31,32]To further verify the mechanical stability of these polymorphs, the elastic constants are calculated with the strain-stress method. Besides, the bulk modulusBand the shear modulusGare estimated via the Voigt-Reuss-Hill approximation by using the obtained elastic constants Ci j.[33,34]Young modulus and Poisson ratio are calculated in accordance with the formulasY=9GB/(3B+G)andv=(3B-2G)/(6B+2G). The theoretical Vicker’s hardness is estimated by the Chen model.[35]The details of convergence tests have been described elsewhere.[36-38]

3. Results and discussion

By employing the crystal structure prediction of the CALYPSO code at ambient pressure,a new orthorhombicCmcmstructure for ScB4is predicted successfully. The orthorhombicCmcmstructure includes four ScB4in a unit cell,with the equilibrium lattice parameters ofa=5.392 ˚A,b=3.158 ˚A,c=10.194 ˚A,α=β=γ=90°under ambient pressure.There are two inequivalent atom positions inCmcm-ScB4. Sc atoms occupy the Wyckoff positions 4c(0,0.9025,1.25),and B atoms occupy the Wyckoff positions 16h(-0.8298,0.6328,0.9221).Each Sc atom inCmcm-ScB4is surrounded by twelve boron atoms, which is similar to that in ScB3(ScB12, shown in Fig.1(b)). The polyhedral view of this structure(Fig.1(a))reveals the fascinating B-Sc-B sandwiches stacking order along thec-axis. At high pressure, we find a unique orthorhombic structure with thePnmaphase to be most stable. At 20 GPa,the optimized lattice constants area=7.035 ˚A,b=2.944 ˚A,c=7.408 ˚A,α=β=γ=90°,which is shown in Fig.1(c).

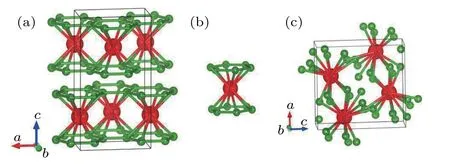
Fig. 1. The crystal structure of the predicted Cmcm-ScB4andPnma-ScB4.Large and small spheres represent Sc and B atoms.

We also measure the formation enthalpies of the considered structures of ScB4from 0 GPa to 100 GPa. For comparison, CrB4(No. 71,Immm), FeB4(No. 58,Pnnm), MnB4(No. 14,P21/c), and ReP4(No. 61,Pbca) are also considered as the potential phases for ScB4, hereafter defined as CrB4-, FeB4-, MnB4-, and ReP4-type structures. The formation enthalpy of ScB4is calculated by the formula ΔH=H(ScB4)-H(Sc)-4H(B). Figure 2 presents the formation enthalpy of six phases as a feature of pressure for ScB4, and it can be clearly seen that the predictedCmcmstructure is energetically more favorable than the other structures at ambient pressure. As the pressure increases,thePnmaphase becomes the most stable when the pressure is higher than about 18 GPa.

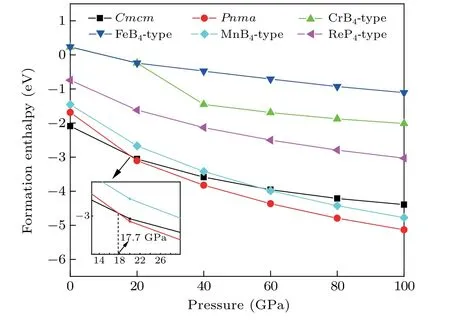
Fig.2.The formation enthalpy-pressure diagrams for ScB4 with six different structures.

In order to find the relative stabilities between the two phases and other scandium borides, the relative enthalpypressure diagrams were plotted. We choose ScB2(space group:P6/mmm) and ScB12(space group:Fm-3m) as the competing phases in our calculations. It can be seen from Fig. 3 that the competing phase ScB2+ScB12is more stable than others at low pressure. When the pressure is increased to 38 GPa,the predictedPnmaphase becomes the most stable phase.

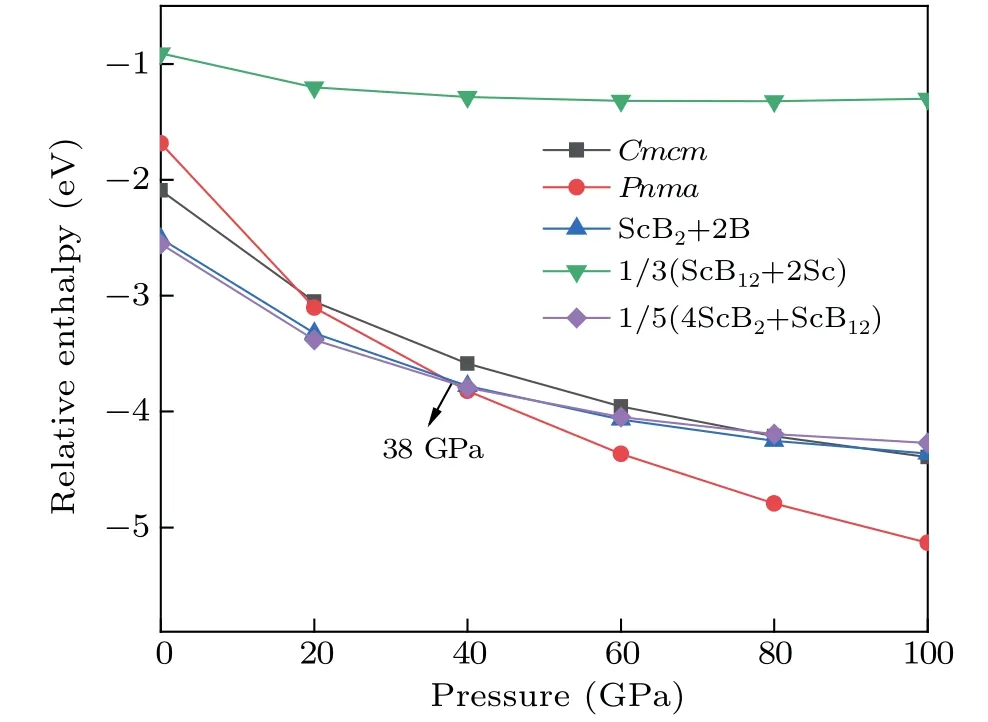
Fig.3. The relative enthalpy-pressure curve of the Cmcm and Pnma phases with its respective competing phases.

The convex hull plots of the Sc-B system at the selected pressures are constructed in Fig.4. As we know,a compound with a formation enthalpy lying on the convex hull is thermodynamically stable. We can expect that this compound can be synthesized in the experiment at their stable pressures.In comparison, the unstable or metastable stoichiometries are above the convex hull. The convex hull of Sc-B compounds at different pressures is performed,which is shown in Fig.4. Here we choose ScB2(space group:P6/mmm) and ScB12(space group:Fm-3m) as the competing phases in our calculations.Note that ScB15and ScB19are not considered here due to the large size of the intercalated structures, although these two compounds have been reported experimentally.[39,40]From Fig. 4(a), we can find that all enthalpies of the formation of the three compounds are negative. They are all stable against all decomposition reactions into the pure elements.ForCmcm-ScB4,it does not locate at the convex hull’s strong curve,indicating it is unstable and is going to decompose under ambient pressure. In Fig. 4(b), the proposedPnma-ScB4phase lies right on the convex hull. Through the above discussion, we can conclude that thePnmaphase becomes the ground state beyond 38 GPa.

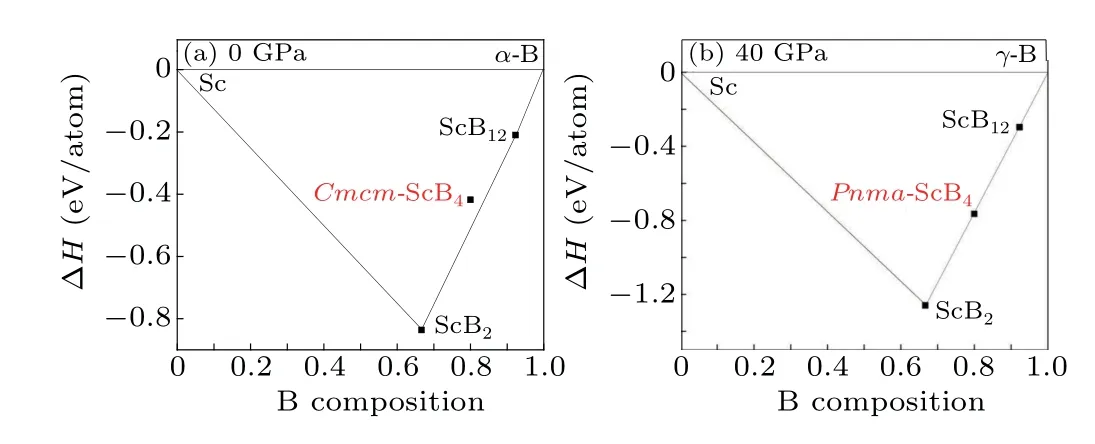
Fig.4. The convex hulls of ScB4 at the pressure of(a)0 GPa and(b)40 GPa.The solid line denotes the convex hull.

Dynamical stabilities are an important indicator of the existence of structures.We performed the phonon dispersion calculations forCmcm-ScB4in 0 GPa andPnma-ScB4structures at 20 GPa and 40 GPa(Fig.5). As can be seen from Fig.5,no imaginary phonon frequency was found in the Brillouin zone ofCmcm-ScB4andPnma-ScB4structures,indicating that they are dynamically stable.

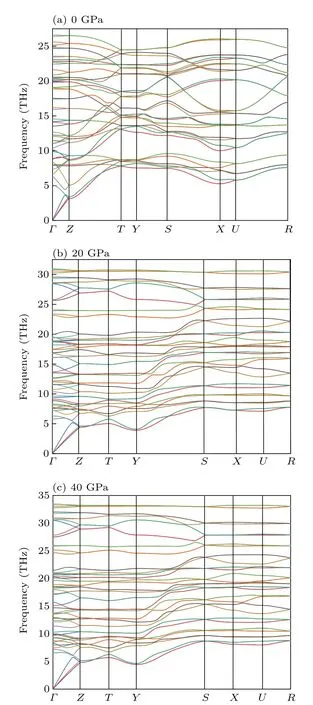
Fig.5.Phonon dispersion curves of Cmcm ScB4 at(a)0 GPa,(b)Pnma ScB4 at 20 GPa,(c)Pnma ScB4 at 40 GPa.

To investigate the elastic stability ofCmcmandPnmaphases for ScB4, we calculated its elastic constants using the stress-strain method. Table 1 lists the calculated elastic constants of the two phases,also together with the results of other transition terborides. For comparison,the previously reported elastic constants of TMB4(TM=Cr,Fe,Mn,Y,Hf)are also considered in this paper. For an orthorhombic crystal, the independent elastic stiffness tensor consists of nine components ofC11,C22,C33,C44,C55,C66,C12,C13,andC23. The mechanical stability is based on the following:

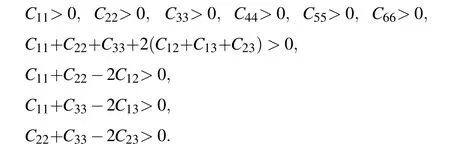
From Table 1, we can verify thatCi jofCmcmandPnmaphases meet the above stability criteria, indicating that they are all mechanically stable. So that, ScB4is both mechanically and dynamically stable at ambient pressure and high pressure. ForCmcm-ScB4, the values of calculatedC33are a lot lower than those ofC11andC22,indicating that the bonding strength along the [001] direction is far softer than that along the [100] and [010] directions. Meanwhile, compared to thec-axis,Cmcm-ScB4is difficult to compress along theaandbaxes. But inPnma-ScB4, the values of calculatedC11are a lot lower than those ofC22andC33, indicating that it is difficult to compress along thebandcaxes. Sadly, no experimental data is available for comparison. Our findings may therefore be a guideline for future studies and applications of 3d transition metal borides under high pressures. Accurate elastic constants are helpful to understand the mechanical properties and provide beneficial information to estimate the properties of a material. ScB4has the bulk modulus of 204 GPa and 284 GPa forCmcmandPnmaphases,which are larger than that of the YB4. The shear modulus of a material is well known to measure its resistance to shear deformation. The calculated shear module ofCmcm-andPnma-ScB4are 184 and 217 GPa, respectively, which are close to that of FeB4. It is expected that they can withstand the shear strain to a large extent. The results of Young’s modulus and Poisson’s ratio are given in Table 1. The large Young’s moduli values ofCmcmandPnma-ScB4(424 and 519,respectively)indicate its strong capability of resisting tension and pressure in the range of elastic deformation. Poisson’s ratio indicates that the relative direction of material bonding has an important influence on the hardness of the material. For covalent materials,the usual valuevis 0.1,and for metal materials,0.33. Among these compounds,Cmcm-ScB4has thevof 0.153 andPnma-ScB4has thevof 0.196, which suggests a degree of covalent bonding for both phases. TheG/Bratio indicates the ductility or brittleness of a material,G/Bless than 0.57 means the material is ductile,otherwise brittle. The calculatedG/Bratio ofCmcm- andPnma-ScB4is implying its brittle nature. All of these excellent mechanical properties strongly suggest that ScB4is a potential candidate to be incompressible and hard materials. The hardness of materials can be measured using an empiric formulaHv=2(K2G)0.585-3 whereK=G/Bdenotes the Pugh’s modulus ratio. Using this model, we calculate the hardness ofCmcm- andPnma-ScB4to be 34.5 GPa and 31 GPa,respectively. We also note that the order of hardness value for the structures considered here is concluded as follows: YB4(17.04 GPa)＜FeB4(24.2 GPa)＜Pnma-ScB4(31 GPa)＜Cmcm-ScB4(34.5 GPa)＜MnB4(38.7 GPa)＜CrB4(45.1 GPa)＜HfB4(45.7 GPa). This result suggests that ScB4has low mechanical strength and does not become a superhard material. Because of the high boron concentration,3D boron networks are not expected to enhance the strength of ScB4. Therefore, ScB4is expected to have mechanical properties consistent with those of other transition metal borides.Of course,these properties need further theoretical and experimental studies.

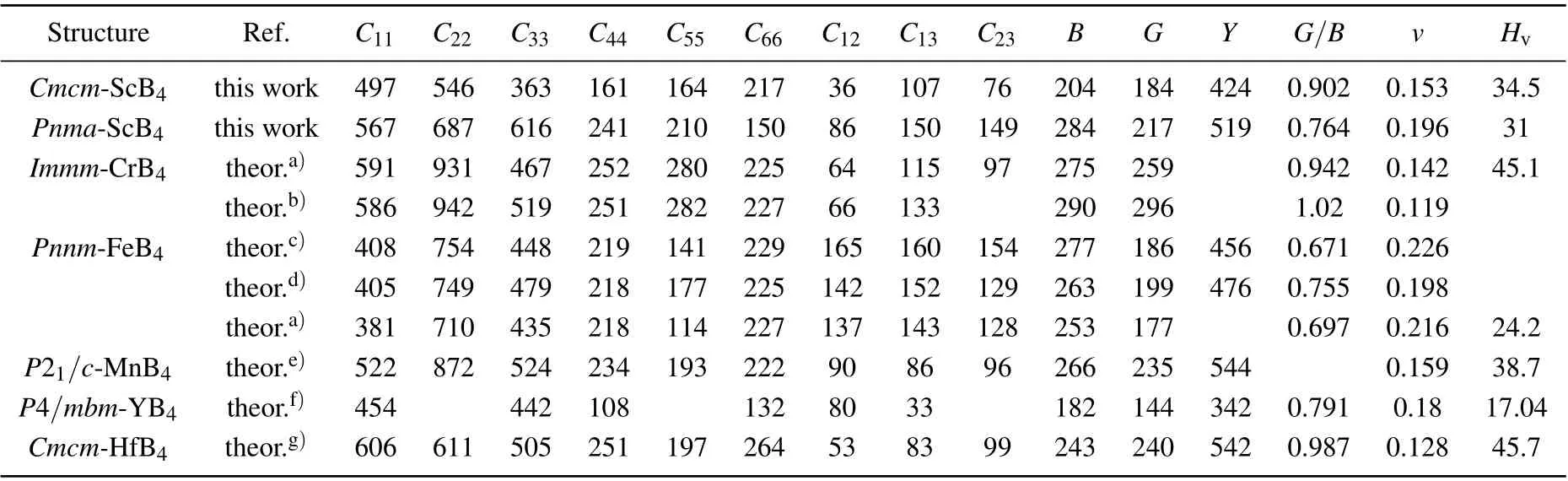
Table 1. The calculated elastic constants Cij (GPa),bulk modulus B(GPa),shear modulus G(GPa),Young’s modulus Y (GPa),G/B,Poisson’s ratio v,and hardness Hv (GPa)for ScB4 in comparison with available theoretical results.

To understand the mechanical properties of ScB4,the total and partial densit of states ofCmcm-ScB4andPnma-ScB4were calculated,shown in Fig.6. These two phases show similar metallic features because of finite DOS at the Fermi level.As seen from Fig. 6(a), we can find that in the region from 15.2 to-6.5 eV, the contributions are primarily contributed by the B-2s and B-2p orbitals with slight contributions of Sc-3d. From-6.5 eV to theEF,B-2p orbitals mostly contribute to the DOS.In Fig.6(b),there is no clear overlap of B-2p and Sc-3d electron in the range of-16.5 and 0.7 eV.As seen from Fig. 6, there is a deep valley, namely, a pseudogap of DOS,which is the borderline between the bonding and antibonding states. The presence of pseudogap will increase the structural stability of ScB4.

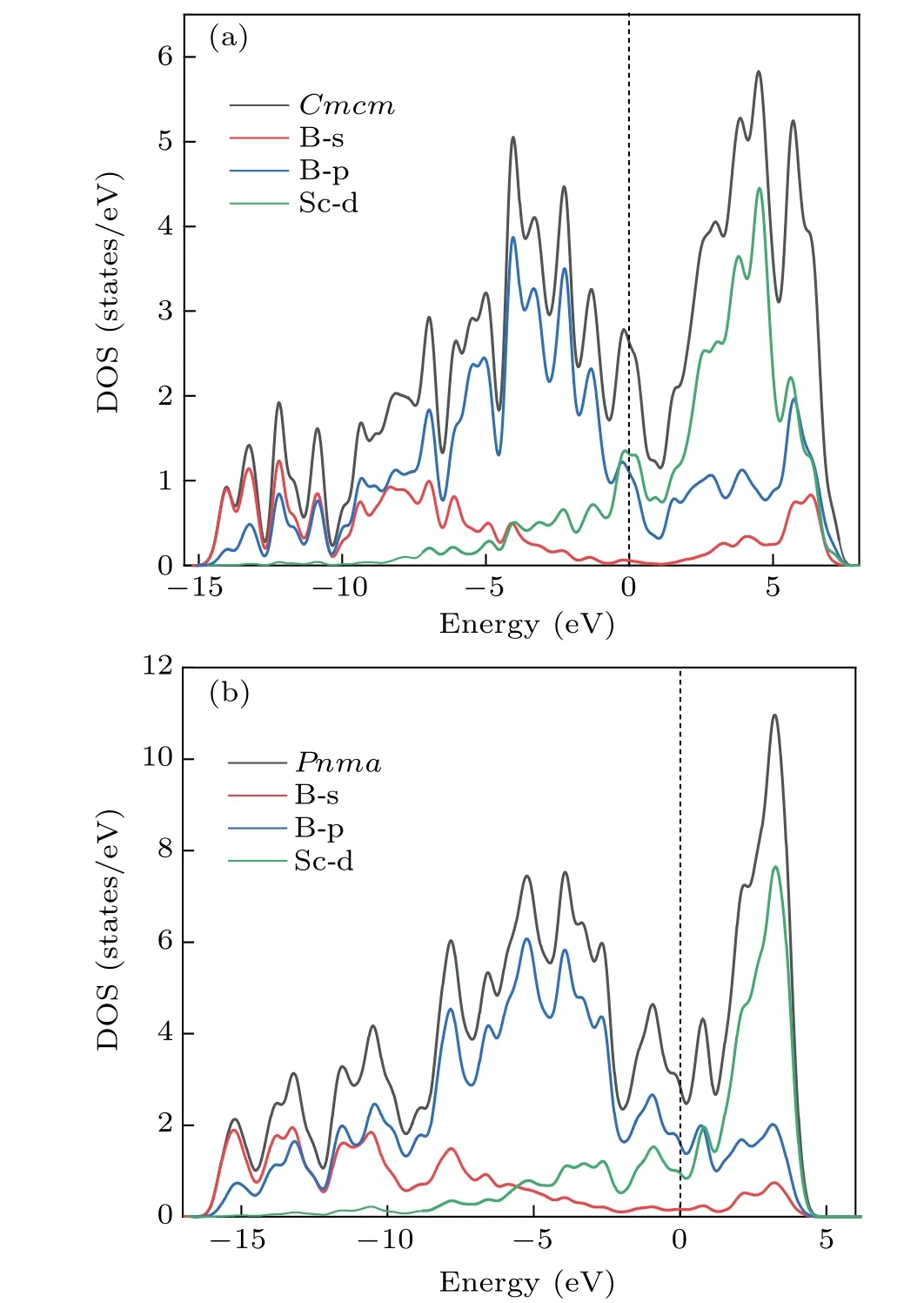
Fig. 6. Total and partial densit of states for (a) Cmcm-ScB4 and (b) Pnma-ScB4.

The electronic localization function(ELF)is widely used to describe and visualize chemical bonding.The ELF is a contour chart in real space with values ranging from 0 to 1. In general, ELF=1 indicates the localized features of covalent bonds or lone pairs, ELF = 0.5 indicates the probability of electron-like gas pairs, and ELF=0 indicates a completely off-domain. We plotted the contours of ELF=0.75 and(001)plane forCmcm-ScB4in Fig.7(a), we can see six-membered ring layers ofCmcm-ScB4.High electron localization between B atoms can be observed, suggesting strong covalent B-B bonds. Besides, we also plotted the (102) plane forCmcm-ScB4in Fig.7(b),and there is a strong Sc-B covalent bonding in theCmcm-ScB4,which is a weaker chemical bond than the B-B bond. The strong B-B and Sc-B covalent bonds contribute significantly to hardness and structural stability.

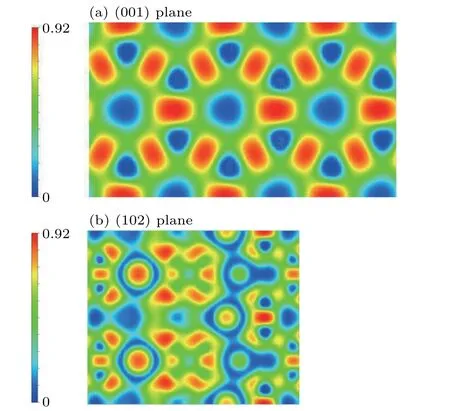
Fig. 7. The contours of the electronic localization function of the Cmcm-ScB4 on the(001)plane(a)and(102)plane(b).

4. Conclusion

In summary, we have predicted two novel boron-rich ScB4with orthorhombicCmcmspace group at ambient pressure andPnmaspace group at high pressure through the PSO technique. In the meantime, the structural properties, phase stability,mechanical strength,and electronic properties of the two phases have been systematically investigated in the firstprinciples calculations. It is illustrated that the predicted two phases are dynamically and elastically stable. The calculated hardness of theCmcmphase is 34.5 GPa, which is a potential hard material. Moreover,the electronic localization function analysis has demonstrated that the strong covalent B-B and Sc-B bonding play a key role in the incompressibility and hardness of ScB4.We look forward to furthering high-pressure work on the synthesis of the superhard material.