Magnon bands in twisted bilayer honeycomb quantum magnets*

Xingchuan Zhu(朱兴川) Huaiming Guo(郭怀明) and Shiping Feng(冯世平)

1Department of Physics,Beijing Normal University,Beijing 100875,China

2Key Laboratory of Micro-Nano Measurement-Manipulation and Physics(Ministry of Education),Department of Physics,Beihang University,Beijing 100191,China

Keywords: magnon bands,twisted bilayer,quantum magnets,linear spin wave theory

1. Introduction

The recent discovery of the correlated insulator and unconventional superconductivity in twisted bilayer graphene has attracted intense interests.[1-8]By rotating the layers to a small angle, a misalignment induced in the bilayer system introduces a long-period moir´e superlattice. Such a superlattice therefore modulates the electronic structure,and leads to nearly flat band at the magic angles. These bands become so narrow that the electronelectron correlations dominate over kinetic energy, giving rise to the above correlated quantum phases.[9]Since twisted bilayer graphene is relatively simple and highly tunable, it is anticipated that this system can serve as an ideal platform to investigate the strongly-correlated physics.

Moir´e superlattices have also been employed to engineer flat bands in other two-dimensional (2D) materials, such as twisted double-bilayer graphene, trilayer graphene, and twisted bilayer of the transition metal dichalcogenide, where rich correlation phenomena have been revealed.[10-19]While research has been primarily centered on twisted electronic systems,there appear theoretical studies addressing the remarkable physical properties in twisted Kitaev bilayers[20]and twisted optical lattices.[21,22]It is accepting that twisting is a simple and general approach to creating exotic quantum matter.

Recently rapid progress in 2D magnetic atomic crystals has been made.[23-27]Various monolayer and multilayer van der Waals (vdW) magnetic materials have been discoveried, and different kinds of ferromagnetic(FM) and antiferromagnetic (AFM) orders have been observed.[28-36]The 2D vdW magnetic materials have a huge potential to create novel functional devices,and have important applications in the next-generation nanoelectronics.[37-42]Of course, they are also important in fundamental research. The physics can be described by a generalized Heisenberg spin Hamiltonian,and a broad range of parameter regimes can be realized in a rich variety of materials. All three spin Hamiltonians,i.e., Ising,XY, and Heisenberg models, can be recovered in specific limits.[43-46]Besides,external perturbations, such as gating, strain,etc., can further tune the range of model parameters.[47-51]These make the magnetic 2D materials into an ideal platform to examine the well-established theories[52-54]and explore new quantum phases.[55-57]

Motivated by these advances in the studies of the twisted 2D materials and 2D magnetic materials, we study how the twist alters the magnon bands in twisted bilayer honeycomb quantum magnets here. We keep the intralayer FM coupling, and study the magnon bands with interlayer FM and AFM couplings in AA(AB)-stacked and twisted bilayer quantum magnets. Our study is closely related to the rapid experimental progress in two-dimensional magnetic materials.

2. AA-stacked honeycomb magnets

Twisted bilayers are characterized by non-zero angleθbetween two honeycomb layers. Since the twist may be performed based on AA-stacked bilayer,we start from the spin-1/2 Heisenberg model on this geometry,which can be written as

Using Holstein-Primakoff (HP) transformation, the spin operators are expressed in term of bosonic creation and annihilation operators. In the FM case,the transformation in the linear spin-wave theory is defined as

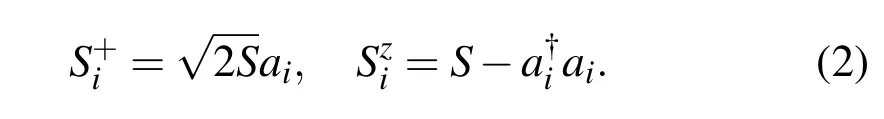
After ignoring a constant and four-operator terms,the resulting bosonic tight binding Hamiltonian becomes

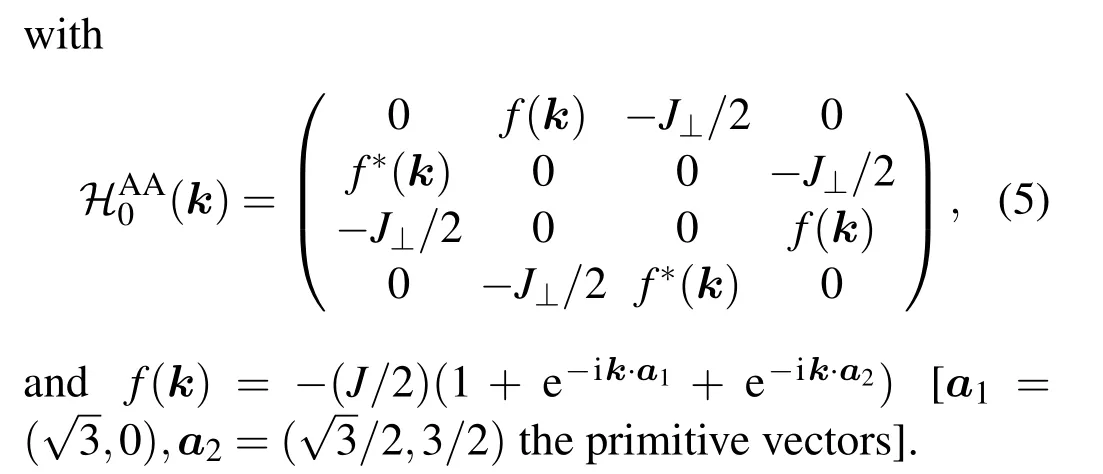
With a unitary transformationψk=U(k)φk(U(k)†U(k)=I), the above Hamiltonian is directly diagonalized, and the spectrum contains four branches:(3J+J⊥)/2±J⊥/2±|f(k)|. The magnon band structure is shown in Fig.1. Compared to that of single-layer honeycomb magnet,the Dirac points are shifted upward and downward byJ⊥/2,which is exactly the same as that of AA-stacked graphene except for an overall translation of 3J+J⊥/2.

Fig. 1. (a) The magnon band structure of AA-stacked FM bilayer.(b) The magnon bands along the high symmetry points in the first Brillouin zone, which are shown in the inset. The parameter is J⊥/J=0.17.

Now we turn to consider the case with interlayer AFM exchange,i.e.,J⊥＜0, while the intralayer coupling remains FM coupling. The following magnetic configuration is assumed: the spins in layer 1 (2) are along the positive(negative)zaxis. The HP transformation in layer 1 is the same as that in Eq.(2).In layer 2,the spin is in the opposite direction, thus the spin operators write as the above Hamiltonian in the momentum space can be written as

and the Dirac point is slightly shifted downward, and the dispersion remains linear. As shown in Fig. 2, the magnon spectrum is almost the same as that of the singlelayer FM case, suggesting the magnon excitations from different spin alignments are decoupled.

Fig. 2. (a) The magnon band structure of AA-stacked FM bilayer with interlayer AFM exchange. (b) The magnon bands along the high symmetry points in the first Brillouin zone. The parameters are the same as those of Fig.1.

3. AB-stacked honeycomb magnets

Next we consider AB-stacked bilayer quantum magnets,which can be viewed as rotating AA-stacked bilayer byθ=60°. In the intralayer and interlayer FM case,the bosonic tight binding Hamiltonian is

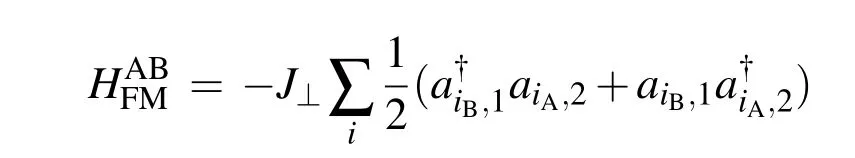
which are quadratic inknear the Dirac points.

Fig.3. The magnon bands along the high symmetric lines in the first Brillouin zone for AB-stacked bilayers with: (a) the interlayer FM coupling; (b) the interlayer AFM coupling. Insets of both figures show the enlarged plots of the magnon bands near the Dirac point.

Then we change interlayer coupling AFM. The bosonic tight binding Hamiltonian becomes

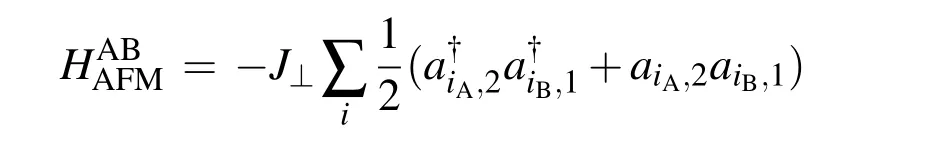
4. Twisted bilayer quantum magnets

By taking any vertical bond in AA-stacked bilayer as the axis,the twisted bilayers are generated by rotating one layer around the axis, while the other layer remains fixed. The periodicity is maintained for commensurateθ, when a certain site of one layer ends up exactly over a site of the other after the rotation. The Bravais lattice of the superstructure is hexagonal with the two unit vectors:L1=ma1+na2andL2=-na1+(m+n)a2. Each supercell containsN=4(m2+mn+n2)sites.[58,59]The twist angle writes as

In the following, we consider the commensurate twist angles 21.8°, 6.01°, and 3.89°, which correspond to(m,n) = (2,1),(6,5),(9,8), respectively. The case of smaller angles have too large supercells to deal with using our computer, and thus instead we calculate the magnon spectrum using the low-energy continuous theory near the Dirac points.[64,65]

The nearest-neighbor intralayer FM coupling are considered with the strength as the energy scale. The strength of interlayer coupling between sitesriandrjis given byJi j=J⊥e-[(|ri-ri|-d0)/ξ], where the parameters are set asJ⊥/J=-0.17,d0= 0.335 nm, andξ=0.0453 nm.

Fig.4. Magnon band structures of twisted bilayers with twist angles of 21.8°,6.01°,and 3.89°: (a)-(c)the interlayer FM coupling;(d)-(f) the interlayer AFM coupling. The intralayer couplings are FM case in all figures. We also plot the magnon spectrums without interlayer coupling(dashed red lines). To compare the Dirac velocity,the Dirac points are moved to the same positions as those in twisted bilayers.

The magnon spectrums are show in Fig. 4. Since thezcomponent of each Heisenberg term generates a positive potential in the HP transformation, the bands are shifted upward compared to the cases without the interlayer coupling. The Dirac cones are preserved for the studied angles. In the interlayer FM cases, while the slopes are almost unchanged for large twist angles(θ=21.8°,6.01°), there is a clear reduction for small angleθ=3.89°. The behavior is very similar to that of twisted bilayer graphene.[62,63]It is expected that the magnon bands becomes flatting as the angle is further decreased. In contrast,the spectrum of the interlay AFM case differs little from that of the single-layer quantum FM case, further verifying the spin excitations of opposite spin orientations do not couple with each other.

Fig. 5. Comparison of the low-energy magnon bands between the continuous theory and exact tight-binding calculation with the FM interlayer coupling. Here the twist angle is θ =3.89°.

5. Conclusions

The magnon bands of both the bilayer and twisted bilayer honeycomb quantum magnets are studied using linear spin wave theory. The interlayer ferromagnetic order but two kinds of intralayer exchange couplings are considered. When the two layers are ferromagnetically coupled, the linear dispersions near the magnon Dirac points are preserved, and their slopes are reduced with the decrease of the twist angles. For the interlayer antiferromagnetic case, we find that the two monolayer magnon dispersions are usually decoupled due to the opposite orientations of the spins in the two layers. Finally a low-energy continuous theory is developed for the small twist angles,and fits well with the exact tightbinding calculations.

Experimentally there have revealed intrinsic magnetism in various atomically thin crystals. Among them,CrX3(X=Cl,Br,I)is a family of 2D honeycomb quantum magnets. Specifically, intralayer ferromagnetism and interlayer antiferromagnetism has been observed in bilayer CrI3.[72-75]Besides,it has been proposed that the interlayer exchange coupling can be tuned between AFM and FM by changing the interlayer stacking order.[76]Thus based on these bilayer honeycomb quantum magnets, our results may be experimentally observed using the state of the art measurements, such as inelastic neutron scattering and magneto-Raman spectroscopy.[77]