Nonlocal advantage of quantum coherence and entanglement of two spins under intrinsic decoherence*

Bao-Min Li(李保民) Ming-Liang Hu(胡明亮) and Heng Fan(范桁)

1Institute of Physics,Chinese Academy of Sciences,Beijing 100190,China

2School of Physical Sciences,University of Chinese Academy of Sciences,Beijing 100190,China

3Songshan Lake Materials Laboratory,Dongguan 523808,China

Keywords: quantum coherence,quantum entanglement,intrinsic decoherence

1. Introduction

Quantum coherence originates from the superposition principle of the basis states,and it is different from that of the interference phenomenon in classical physics.Among the various characterizations of quantumness (e.g., entanglement,[1]quantum discord,[2]etc.), quantum coherence is the the most fundamental one, and in some sense, the essence of quantum correlations,[3,4]although it characterizes quantumness of the whole systemS, whereas quantum correlations are related to the interrelation between subsystems ofS. Moreover, quantum coherence is an indispensable resource for achieving the quantum advantage of quantum computation, quantum communication,and quantum metrology tasks.[5]

Due to its fundamental role in the basic theory of quantum mechanics and applications in new quantum technologies, it is necessary to quantify coherence. In 2014, Baumgratz and his coauthors[6]constructed a resource theoretic framework of coherence,and proposed to quantify the amount of coherence in a stateρby its “shortest distance” to the set of incoherent states. Some well-defined measures within such a framework include thel1norm and relative entropy of coherence,[6]the entanglement-based coherence measures,[7]the robustness of coherence,[8]the intrinsic randomness of coherence,[9]the coherence of formation,[10]the maximum relative entropy of coherence,[11]and the skew information measure of coherence.[12]There are also several coherence measures defined within slightly different frameworks, see Ref.[4].

Based on the above measures, researchers further analyzed quantitatively the role of quantum coherence in specific quantum computational tasks. Some notable progresses include the advantage of quantum state merging,[13]deterministic quantum computation with one qubit,[14]the Deutsch-Jozsa algorithm,[15]the Grover search algorithm,[16]and the phase discrimination tasks.[8,11,12]Quantum coherence is also a resource for enhancing efficiency of the quantum heat engine.[17]As a fundamental concept in quantum theory, it has also been used to interpret the wave-particle duality[18,19]and various form of quantum correlations such as quantum entanglement[7,20]and quantum discord.[20-23]

From a practical point of view, decoherence remains a main obstacle for carrying out quantum computation tasks, and different systems may face different sources of decoherence.[5]Hence it is significant to give a quantitative description of the decoherence process. The various coherence measures facilitate the development of such a task. In recent years, some studies, including the quantitative analyses of the decoherence process of different systems,[24-27]the evolution equation of coherence under completely positive and trace preserving operations,[28]and the conditions for freezing coherence,[29-32]have been performed. Effects of active operations on coherence, such as the coherence-preserving operations,[33]the cohering power of a channel,[34-36]and the energy cost for creating coherence,[37]have also been discussed.

In this work, we explore the nonlocal advantage of quantum coherence (NAQC) and entanglement under intrinsic decoherence.[38]The NAQC was defined based on steered coherence under local operations and classical communication.[39,40]It reveals a kind of quantum correlation which is stronger than entanglement (it is also stronger than Bell nonlocality for the two-qubit states[41]). The shareability of NAQC by sequential observers,[42]its role in studying quantum criticality of the spin systems,[43]and its behavior under noisy channels,[44-46]have been explored. For two spins under intrinsic decoherence,we will show that the decay of both the NAQC and entanglement can be noticeably suppressed by tuning the system parameters to appropriate values.

2. Measures of NAQC and entanglement

As a preliminary, we recall how to quantify NAQC and entanglement in a (d×d)-dimensional stateρAB. First,the NAQC was defined based on the resource theory of coherence,[6]and one can obtain different criteria for capturing NAQC inρABby using different coherence measures.[39]We will use the relative entropy of coherence which has a clear physical interpretation.[10]For ad-dimensional stateρ,it was defined to be the relative entropyS(ρ‖δ) minimized over alld-dimensional diagonal density operatorδin the reference basis{|i〉},and can be solved analytically as[6]

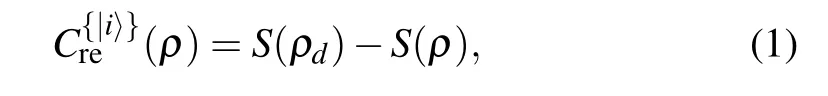
whereρd=∑i〈i|ρ|i〉|i〉〈i|,S(ρd)=-tr(ρdlog2ρd)is the von Neumann entropy ofρd,and likewise forS(ρ).

Based on Eq. (1), one can derive the criterion for capturing NAQC. There are two different frameworks related to such a problem, both of which are formulated by first measuring one of the mutually unbiased observables{Ak}(e.g.,Ai) on partyAand then calculating the average coherence of the ensemble{ρB|Aai,pa|Ai}, withpa|Aibeing the probability of obtaining the outcomeaandρB|Aaithe corresponding postmeasurement state ofB. But for the first framework,the coherence ofρB|Aaiis calculated with respect to the basis spanned by the eigenbasis ofAj/=Aiand then being averaged over allAj/=Ai,[39]while for the second framework,it is calculated only with respect to the optimal basis spanned by the eigenbasis ofA˜αi, with{A˜αi}being a permutation of the set{Ak}which gives the maximum average coherence of{ρB|Aai,pa|Ai},i.e., one should maximize the average coherence of{ρB|Aai,pa|Ai}over all possible permutations of the set{Ak}.[40]As the criterion formulated within the second framework captures a wider region of NAQC states than that formulated within the first framework,[40]we will make use of it in this paper. Then the criterion for capturing the NAQC inρABcan be obtained as

3. The intrinsic decoherence model

We consider the intrinsic decoherence model, for which the equation of motion for a system described by the Hamiltonian ˆHis given by[38]

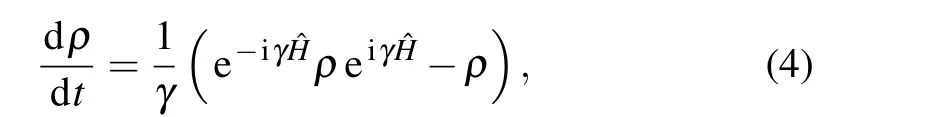
and it is formulated based on the hypothesis that on sufficiently short time steps, the system will evolves in a stochastic sequence of identical unitary transformation instead of evolving continuously and unitary in the whole evolution process, and the decoherence rateγis proportional to this minimum time step.[38]

3.1. Solution of the model

The decoherence model of Eq.(4)is usually solved by expanding its right-hand side(RHS)to the first order inγ,which yields

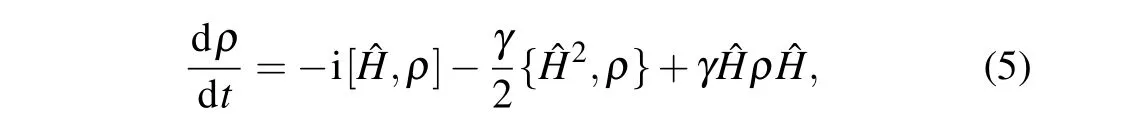
where[]and{}denote,the commutator and anticommutator,respectively. Then by denoting{∈k}and{|ψk〉}the eigenvalues and eigenstates of ˆH,respectively,andakl=〈ψk|ρ(0)|ψl〉,withρ(0) being the initial state, equation (5) can be solved as[49]

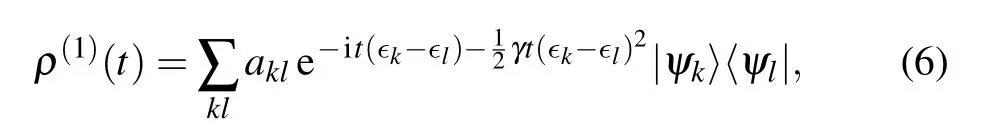
whereρ(1)(t) is introduced for distinguishing the solutions of Eq. (4) with its RHS being expanded to different orders inγ. Based on this solution, decay of Bell nonlocality,[50]entanglement,[51-53]and entropic uncertainty,[54,55]have been extensively investigated.

By further expanding the RHS of Eq. (4) to the order ofγ2,one has

withρ(i j)being a (d×d)-dimensional matrix with one element of 1 in thei-th row andj-th column and all the other elements are zero,then the elements of ˜Λcan be obtained as

and the elements ofρ(t) are given byρi j(t)= ˜ρd(i-1)+j(t).Different fromρ(1)(t)andρ(2)(t),the accuracy of the solutionρ(t)depends on the accuracy for diagonalizing ˆHand ˜Λ.

The NAQC of the thermal states of various spin systems has been studied.[57-59]In this paper,we focus on the intrinsic decoherence effects on NAQC of the spin system.We consider the following Hamiltonian(in units of ¯h):

We consider the cases ofs=1/2 and 1,for which ˆHcan be diagonalized exactly,thus the accuracy of the solutionρ(t)depends solely on the diagonalization of ˜Λ. Fors=1/2, the eigenvalues and eigenvectors of ˆHcan be derived as

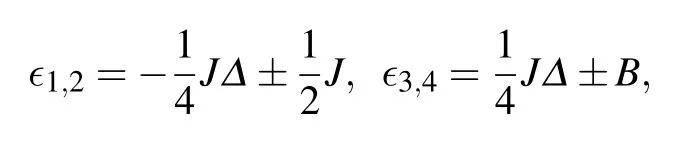
3.2. Comparison of the different solutions

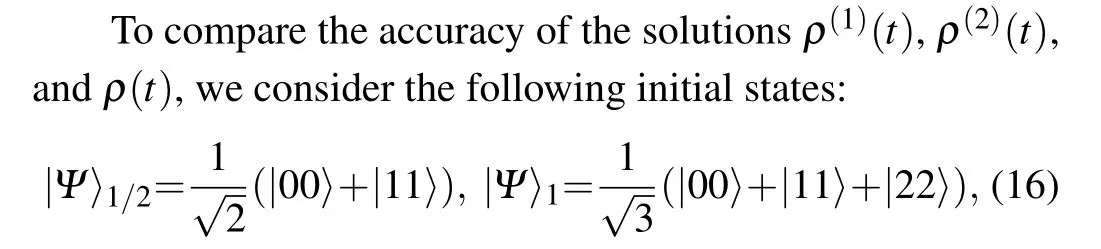
where|Ψ〉1/2(|Ψ〉1)is for the spin-1/2(spin-1)case. We consider the two states for they are useful in quantum information processing tasks such as quantum teleportation.[60,61]

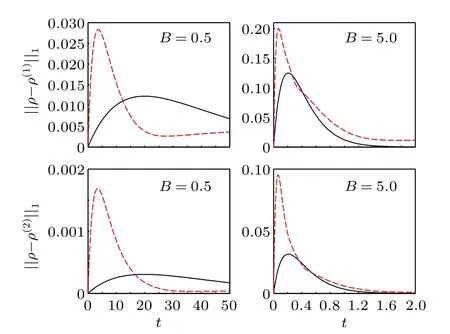
Fig. 1. ‖ρ-ρ(1)‖1 and ‖ρ-ρ(2)‖1 versus t for the initial states |Ψ〉1/2(solid black)and|Ψ〉1 (dashed red)with different B. The other parameters are given by J=1,Δ =0,and γ =0.1.

from which one can see thatρ(1)(t)andρ(2)(t)may yield inaccurate results for certainB,see,e.g.,the solid lines showed in Fig.1. Moreover,whenBγ=kπ(k ∈Z),one has ˜Λ4,4=0,soρ(t)will remain unchanged. But it should note that such an observation does not hold for a general initial state.

For the spin-1 case, as the dimension of ˜Λis still relatively small,it can be diagonalized numerically. In Fig.1,we show the time dependence of the trace norm‖ρ-ρ(1)‖1and‖ρ-ρ(2)‖1withΔ=0 and differentB. In the long-time region, one can see that the three solutions are approximately the same. In the short-time region, however, the accuracy ofρ(1)(t)andρ(2)(t)are relatively low. So when using them as solutions of Eq.(4),one should pay attention to their accuracy.

4. Dynamics of NAQC and negativity

In this section, we useρ(t) obtained from Eq. (12) to calculate the time-evolved NAQC and negativity,and explore their decay behaviors for the initial states of Eq. (16). Occasionally, we also give some intuitive analysis by using the approximate solutions of Eqs.(6)and(8).

4.1. The NAQC

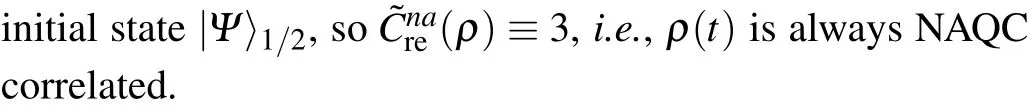
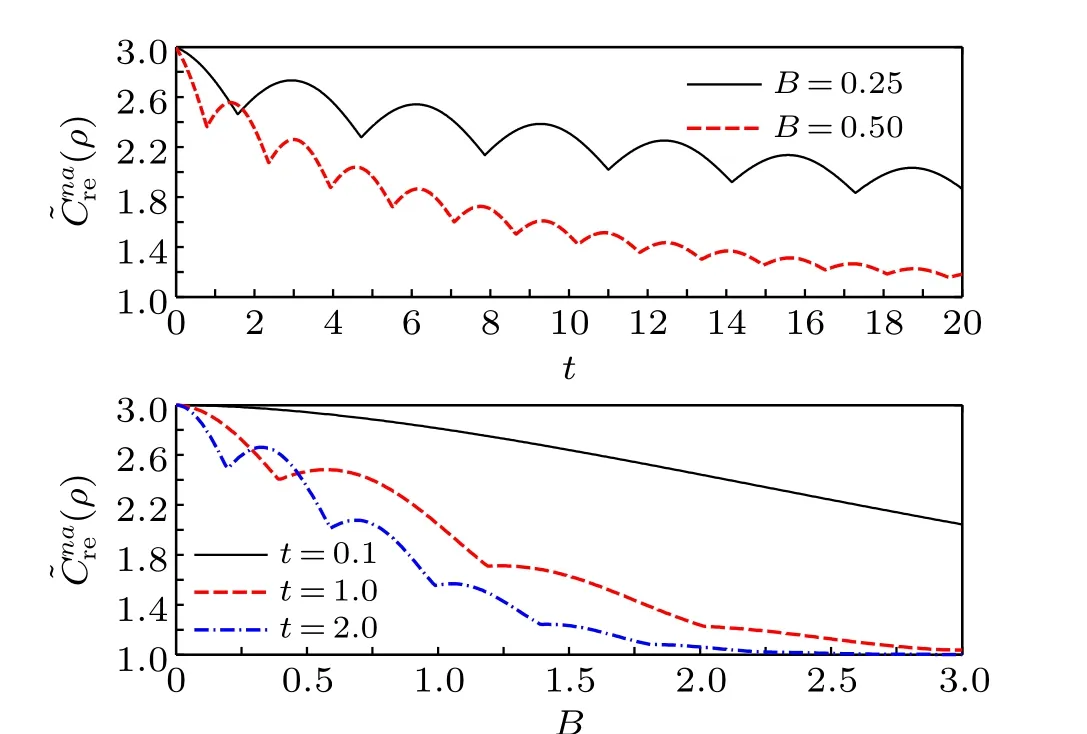
Fig. 2. C˜rnea(ρ) versus t with different B and C˜rnea(ρ) versus B at different times t for the initial state|Ψ〉1/2. The other parameters are given by J=1 and γ =0.1.

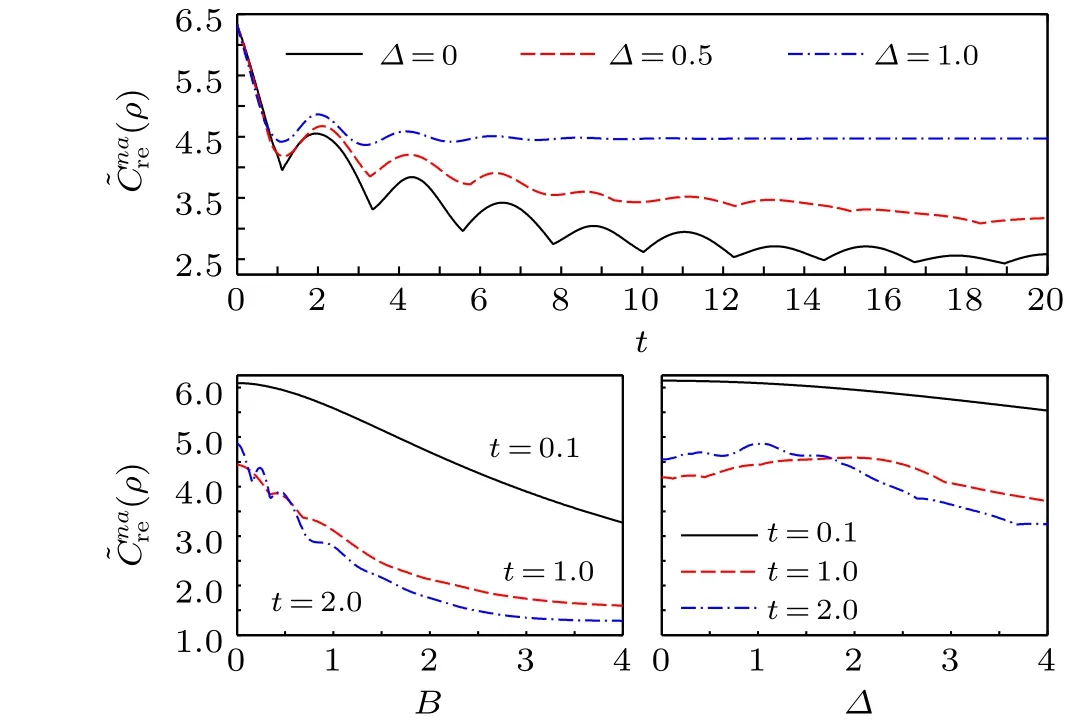
Fig.3. (ρ)versus t with fxied B=0 and different Δ (top),(ρ)versus B with Δ =1 and different t (bottom left), and(ρ) versus Δ with B=0 and different t (bottom right),all for the initial state|Ψ〉1. The other parameters are given by J=1 and γ =0.1.

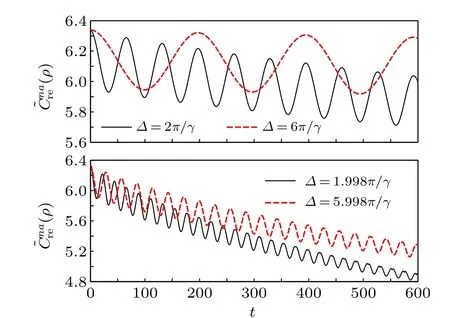
Fig.4.(ρ)versus t for the initial state|Ψ〉1 with B=0 and Δ locating at(top)or in the vicinity of Δ =2mπ/γ (bottom). The other parameters are given by J=1 and γ =0.1.

4.2. The negativity

It has been shown that the NAQC captures a kind of quantum correlation stronger than entanglement.[39,40]Then it is natural to compare decay behaviors of the NAQC with that of the entanglement of the time-evolved stateρ(t) obtained within the framework of intrinsic decoherence. In this subsection,we will consider such a problem,aimed at revealing the similarities and differences between decay behaviors of these two different forms of quantum correlations.

We first consider the spin-1/2 case,for which the negativity ofρ(t)can be obtained analytically as

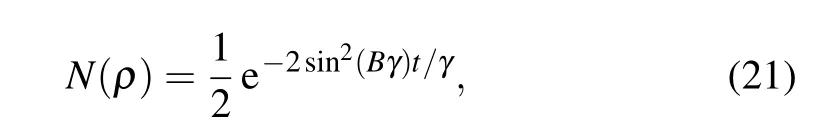
from which one can obtain that whenB=kπ/γ(k=0,1,...),the negativityN(ρ) of the time-evolved state will remain the constant value 0.5, irrespective of the evolution timetof the two spins. For general values ofB,however,N(ρ)will decay exponentially with time and approach to the asymptotic value 0 in the infinite time limit. This indicates that the stateρ(t)is always entangled for the initial state|Ψ〉1/2. As the NAQC ofρ(t)disappears after several rounds of damped oscillations(see Fig.2),this also confirms the finding that what the NAQC captures is a type of quantum correlation which is stronger than quantum entanglement.[39,40]

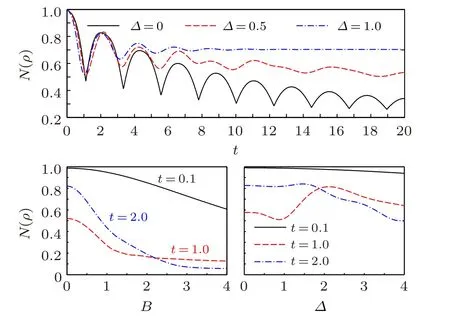
Fig.5. N(ρ)versus t with B=0 and different Δ (top),N(ρ)versus B with Δ =1 and different t (bottom left),and N(ρ)versus Δ with B=0 and different t(bottom right),all for the initial state|Ψ〉1. The other parameters are given by J=1 and γ =0.1.

5. Summary

In summary, we have investigated the decay process of both NAQC and entanglement for two spins within the framework of intrinsic decoherence, and the two spins are coupled via the HeisenbergXXZmodel. We first presented solutionsρ(n)(t) of the intrinsic decoherence model by expanding its decoherence term to then-th order inγ, and then compared its accuracy with the solutionρ(t) obtained by introducing a generalized superoperator. By choosing the initial maximally entangled states, we obtained analytical result ofρ(t) for the spin-1/2 case and numerical result ofρ(t)for the spin-1 case,and showed explicitly thatρ(n)(t) may yield very inaccurate results under certain circumstances. So we used the solutionρ(t) in the subsequent investigation of NAQC and entanglement.

For two spins interact via the HeisenbergXXZmodel with weak transverse magnetic field,the NAQC of the initial maximally entangled states behave as a damped oscillation with the timetevolves,while the negativity decays exponentially(behaves as a damped oscillation) for the spin-1/2 (spin-1) case.Moreover, we have also shown that for the spin-1/2 case, the time-evolved state is independent ofΔand it will be immune of the intrinsic decoherence ifB=lπ/γ(l=0,1,...). For the spin-1 case,the rapid decay of both NAQC and entanglement can be noticeably suppressed whenB=lπ/γ(l=0,1,...)andΔ=2mπ/γ(m=1,2,...). Such a suppression effect can be strengthened by increasingm. This shows that by tuning the system parameters to appropriate strengths,the detrimental effect of intrinsic decoherence can be noticeably suppressed and the quantum correlations of two spins may be preserved for a long time.