Super-sensitivity measurement of tiny Doppler frequency shifts based on parametric amplification and squeezed vacuum state

Zhi-Yuan Wang(王志远), Zi-Jing Zhang(张子静), and Yuan Zhao(赵远)

Department of Physics,Harbin Institute of Technology,Harbin 150001,China

Keywords: squeezed vacuum state,quantum metrology

1. Introduction

Making use of Doppler frequency shifts to measure speed is very important in many applications.[1-4]The measurement precision of Doppler frequency shifts determines the measurement precision of speed. At present, the methods to improve measurement precision are mainly in two aspects: the first is to use non-classical light sources to improve measurement precision,including the precision measurement of phase,[5-10]the measurement of small beam deflection,[11-13]the measurement of gravitational waves,[14-16]and the precise measurement of the magnetic field,[17]and the second is to use a suitable measurement scheme at the receiving end. For example, Fabreet al.[18]gave the standard quantum limit of beam splitting detection when measuring a small beam deflection.Trepet al.[19]used a four-quadrant detector combined with a squeezed light source to measure the transversal displacement beyond shot noise limit. Then they adopted a balanced homodyne detection scheme to reach the Cram´er-Rao bound of information parameters in optical image. Hsuet al.[20]and Delaubertet al.[21]found that balanced homodyne detection was the optimal detection scheme for transversal displacement and the tilt measurement,and proved their theoretical scheme in experiment.

The precision measurement of Doppler frequency shifts also occupies an important position in quantum precision measurement. Vizaet al.[22]used coherent light source and adopted a weak measurement scheme to precisely measure Doppler frequency shifts. Pinelet al.[23]used a weak measurement scheme to accurately measure the frequency modulation range of continuous wave. However,the coherent state belongs to a classical light source. No matter how the detection scheme is optimized, there is an unbreakable quantum Cram´er-Rao bound for the measurement precision. The emergence of quantum state light sources and the maturity of non-linear technology make it possible to break through the Cram´er-Rao bound of coherent light measurement,and to further improve the measurement precision of Doppler frequency shifts.

This paper incorporates a parametric amplification technique and squeezed vacuum state into the detection system of tiny Doppler frequency shifts,and proposes a theoretical measurement scheme of Doppler frequency shifts.For weak signal detection at long distance,the use of parametric amplification is of importance for improving the measurement precision.The scheme adopts the structure of Michelson interferometer to realize the homodyne detection of local light and signal light. Our research finds that when then-order (n ＞0) Hermite Gaussian beam is adopted as the signal light,the Doppler measurement precision can be improved,and the measurement precision of the system can exceed the Cram´er-Rao bound of coherent light through a parametric amplification process and squeezed vacuum state injected. Then we discuss factors influencing the measurement precision in our scheme.

The rest of this paper is organized as follows. In Section 2,the parametric amplification and squeezed vacuum state are used to precisely measure Doppler frequency shifts. In Section 3, the factors influencing tiny Doppler measurement precision are analyzed. In Section 4, some conclusions are drawn from the present study, and the perspectives are also presented,finally.

2. Using parametric amplification and squeezed vacuum state to precisely measure Doppler frequency shifts

As shown in Fig.1,we use a beam splitter BS1(50:50)to divide the laser into local light and signal light. After the signal light passes through an acousto-optic modulator (AOM),its frequency isω2,and then the signal light passes through an atomic pool that performs a parametric amplification process to achieve stimulated Raman scattering (SRS). At this time,the signal light is the Stokes seed light in the SRS process. After exiting from the atomic pool, the intensity of signal light will increase.

Fig. 1. Doppler precision measurement scheme of parametric amplification and squeezed vacuum state. The laser is divided into the local light and signal light by a beam splitter BS1. The signal light passes through an acousto-optic modulator (AOM) to obtain a frequency shift. The mirror M2 moves at a tiny constant speed,and the signal light is amplified by a parametric amplification process. After the squeezed vacuum state is injected,the signal light is incident on a dispersive prism. This process converts the tiny frequency shifts into the transversal displacements of the beam. The local light that is reflected by mirror M1 and the signal light separately pass through a mode converter,which can change their transversal modes. Finally,the transversal displacement d is obtained by balanced homodyne detection(BHD),and then the tiny Doppler frequency shift Δω can be obtained.

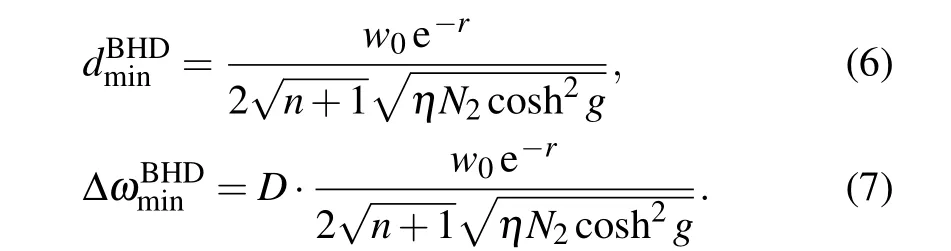
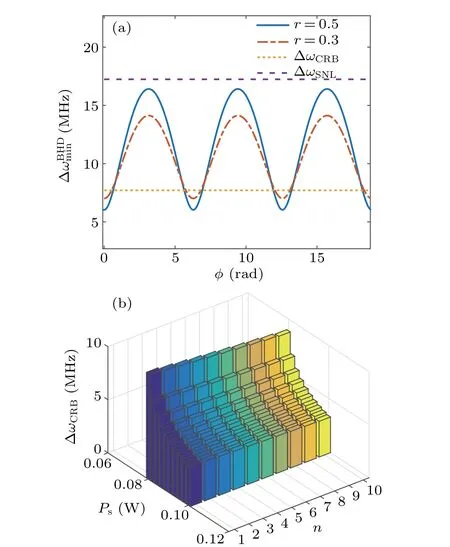
Fig. 2. (a) Relationship between phase difference between signal light and local light and the measurement error of frequency shifts,with parameter amplification factor g=0.When the value of φ is 2kπ,the measurement error of the system has a minimum value,which can break through the Cram´er-Rao bound of coherent light measurement. (b) Relationship among signal light power, signal light order and Cram´er-Rao bound of coherent light ΔωCRB,showing that Cram´er-Rao bound of coherent light decreases as signal light power increases. At the same time, high-order signal light has higher measurement precision.

3. Analysis of factors influencing tiny Doppler measurement precision

In Section 2,we have obtained the value of the transversal displacementdfrom Eq.(4),and the value of the Doppler frequency shift Δω. In this section, we will prove that the precision of our scheme is better than the one with coherent light. We analyze the factors of influencing the Doppler measurement precision, such as the amplification factor and the squeezed factor. At the same time, the modes of local light and squeezed vacuum state can also influence the measurement precision of tiny Doppler frequency shift in our system.

3.1. Influence of amplification factor and squeezed factor on measurement precision

Fig.3. (a)Relationship among measurement precisions of tiny Doppler frequency shifts,squeezed factor r and parametric amplification factor g,n=2,showing that larger amplification factor and larger squeezed factor will reduce measurement error of the system. (b)Diagram of the measurement errorfor different values of amplification factor g and squeezed factor r, indicating that when we choose g=1 and r=0.5, for the signal light in the same order, the measurement precision can exceed the Cram´er-Rao bound of coherent light measurement. (c)Functional diagram of ΔωBHDmin and signal light power. As the signal light power increases, the measurement error of the system will decrease. (d) Relationship between the minimum measurable displacement d of and the SNR of the detection system. When SNR=1 dB (or SNR=0 dB), we can obtain the minimum detectable transversal displacement d of the system. So we can obtain d1min ＜d2min ＜d3min in Fig.3(d). It can be seen that the measurement error of the system will be lower than the Cram´er-Rao bound of coherent light when using parametric amplification and squeezed vacuum state.

It can be seen from Eq.(6)that when the transversal mode order of the signal light is larger, the measurement error of tiny Doppler frequency shift is smaller. As the squeezed factorrand parametric amplification factorgin this system increase, the minimum measurable frequency shift of the system decreases (as shown in Fig. 3(a)). When both the parametric amplification factor and the squeezed factor are 0, the measurement precision of the system at this time cannot exceed the Cram´er-Rao bound of coherent light. After adopting the parametric amplification and squeezed vacuum state injection, the measurement precision of the system breaks through the Cram´er-Rao bound of coherent light (as shown in Fig.3(b)). It verifies the superiority of frequency shift measurement after the parametric amplification and the squeezed vacuum state have been combined. Figure 3(b)shows that for the signal light in Gaussian mode,when the amplification factorg=1 and the squeezed factorr=0.5, the measurement error of Doppler frequency shifts is 14.4%of the error determined by the Cram´er-Rao bound of coherent light. With the increase of the signal light order, the measurement error and ΔωCRBdecrease. It is shown in Fig.3(b)that the measurement errors of Doppler frequency shifts are 17.7%and 18.7%of the Cram´er-Rao bound of coherent light, whenn=1 and 2, respectively. At the same time, as the photon number of signal light increases,our solution can always break through the shot noise limit and the Cram´er-Rao bound of coherent light (as shown in Fig.3(c)).

Figure 3(d) shows that the minimum measurable displacement of the system is determined when the SNR is equal to 1. It can be seen from Eq. (2) that the smallest measurable displacement determines the minimum measurable frequency shift of the system. When we adopt parametric amplification and squeezed vacuum state injection, the SNR of the system is improved, and the measurable displacement is reduced. At this time, the measurement precision of the system is improved. The relevant simulation parameters in this paper areλ=1064 nm,w0=53 μm,the relevant parameters of the dispersive prism in our system are as follows:A=1.60,B=7881 nm-2,C=1.7×108nm-4, base angleγ=15°,base side lengthL=50 cm,loss rateη=96%,and resolution bandwidth RBW=0.3 kHz.

3.2. Influence of mode of local light on measurement precision

According to Eq.(A5)in Appendix A,it can be seen that when the signal light inn-order mode is displaced,the components of the(n-1)-order mode and(n+1)-order mode will be excited. Therefore,for the local light the superposition mode of(n-1)-order and(n+1)-order is also adopted at this time.It will maximize the SNR and the measurement precision. In order to discuss the mode of local light that makes the detection system have the greatest precision, we set the mode of local light to beu2(x)=run-1(x)+teiφun+1(x),whererandtare the weight of the (n-1)-mode and (n+1)-mode in the local light,satisfyingr2+t2=1,andφis the phase difference between (n+1)-order mode and (n-1)-order mode. At this time, we can obtain the positive frequency expression of the local light as follows:

Figure 4 shows the error function of signal light at different orders (n=0, 1, 2, and 3). In particular, whenn=0, a minimum error is obtained atr/t=0,i.e.,un+1(x)is the best mode of the local light at this time.

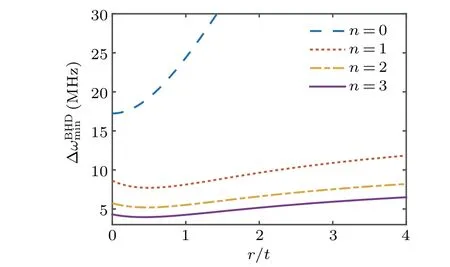
Fig.4.Curves of minimum measurable frequency shift versus energy weight ratio r/t of(n-1)-order mode to(n+1)-order mode for different values of n. When r/t=+1,the SNR of the system reaches maximum,and the measurement error is the smallest at this time.

3.3. Influence of modes of squeezed vacuum state on measurement precision

In addition to the mode of the local light affecting the measurement precision of the system, the mode of the squeezed vacuum state affects the measurement precision of the system. After the local light adopts the best superposition mode,the squeezed vacuum state should also adopt the mode corresponding to the local light. At this time,the photon number difference operator is

In the above formulas,r1andr2are the squeezed degrees of squeezed vacuum state in (n-1)-order mode and (n+1)-order mode, respectively. Therefore, if the measurement precision is required to be higher,the squeezed vacuum state must adopt the same superposition mode as the local light, andr1,r2＞0 must be satisfied. The influences of squeezed degrees of(n-1)-order mode and(n+1)-order mode on the SNR and measurement precision of the system are shown in Fig. 5. It can be seen from Fig. 5(a) that when the squeezed vacuum state has squeezed degrees in both the(n-1)-order mode and(n+1)-order mode,the measurement precision of the system will reach a maximum value. In particular, when the signal light is in the 0-order mode,the measurement precision at this time loses its dependence on the squeezed factorr1. The reason is that the coefficient beforer1in Eq.(13)is 0,so the precision at this time will increase withr2increasing. Figure 5(b)shows that with the increase of the squeezed factorsr1,r2,and the mode order of signal light,the Doppler measurement precision increase. Simulation related parameters are signal light powerPs=0.08 W and loss rateη=96%.

Fig.5. (a)Influences of mode of squeezed vacuum state on precision for different orders of signal light,showing that when the squeezed vacuum state in both(n-1)-order mode and(n+1)-order mode is injected,the measurement precision of our system reaches a maximum value. (b)Influence of squeezed factors r1 and r2 on measurement precision for mode order of signal light n=2,showing that with the increase of r1 and r2,the measurement error of the system decreases.

4. Conclusions and perspectives

Appendix A

In Appendix A, the relevant theoretical formulas about balanced homodyne detection are given. According to the Eq. (B1) in Appendix B, we can give the expression of the positive frequency part of the local light and the signal light as follows:

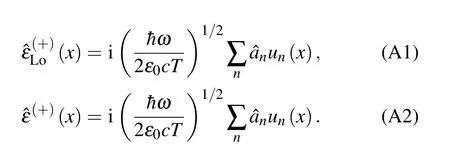
After the two input fields interfere with the 50:50 beam splitter, the positive frequency expressions of the two output fields are expressed as

Then the difference between the photocurrents of the two detectors is

Appendix B

In this section, the quantum theory of electromagnetic field and related theoretical derivation of balanced homodyne detection are given. The electromagnetic field can be expanded by using a set of orthogonal mode basis vectors. The expression of the positive frequency part of the electromagnetic field is

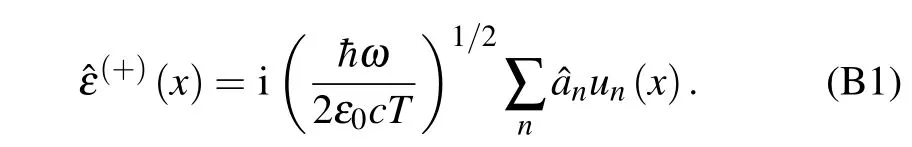
In the above formula,ωis the angular frequency of the electromagnetic field,cis the speed of light,Tis the detection integration time,ε0is the permittivity of free space, ˆanis the annihilation operator of then-order mode,andun(x)is then-order Hermite-Gaussian mode.

The annihilation operator ˆa=〈ˆa〉+δˆais linerarized,and only the average value of then-order Hermite-Gaussian mode is not 0. For the signal light with a transversal displacementd,the positive frequency part of the light field can be written as

Appendix C

In this section, the theoretical derivation of the quantum Cram´er-Rao bound of coherent light measurement is presented.[24]For the coherent light with a transversal displacementd, the photon number distribution at coordinatexobeys the Poisson distribution:

Then the logarithm likelihood function at coordinatexcan be defined as

Then we can obtain the Fisher information expression

For a high-order Hermite-Gaussian beam with a transversal displacementd,the average number of photons at coordinatexsatisfies ¯n(x,d)=N2u2n(x,d), whereN2is the photon number of the signal beam, andun(x,d) is a amplitude expression of a TEMn0mode.

From this we can obtain the Fisher information expression at coordinatexas follows:

It is worth mentioning that the calculation of the quantum Cram´er-Rao bound does not depend on the specific measurement. It can be used as a standard to evaluate the quality of measurements. The closer to the quantum Cram´er-Rao bound the variance of the measurement is, the better the evaluation will be.