Improving the purity of heralded single-photon sources through spontaneous parametric down-conversion process*

Jing Wang(王静) Chun-Hui Zhang(张春辉) Jing-Yang Liu(刘靖阳)Xue-Rui Qian(钱雪瑞) Jian Li(李剑) and Qin Wang(王琴)

1Institute of Quantum Information and Technology,Nanjing University of Posts and Telecommunications,Nanjing 210003,China

2Broadband Wireless Communication and Sensor Network Technology,Key Laboratory of Ministry of Education,Nanjing University of Posts and Telecommunications,Nanjing 210003,China

Keywords: quantum information,quantum communication,nonlinear optics

1. Introduction

Spectrally factorable photon pair has attracted a lot of attention from scientists since it can furnish a highpurity heralded single-photon source, which is essential for the application of quantum information processing,e.g., quantum cryptography,[1,2]quantum teleportation,[3]and quantum dense coding.[4]Both spontaneous parametric down-conversion(SPDC)and spontaneous four-wave-mixing(SFWM) can generate photon pairs, and the former is more widely utilized compared with the latter due to its simplicity and convenience in experimental preparations.In a SPDC process,when a laser incidents onto a piece of nonlinear crystal,it spontaneously generates photon pairs,one is denoted as the signal photon and the other is named the idle photon. It obeys both the laws of energy conservation and momentum conservation during the SPDC process. In most cases, the signal and the idler photons are spectrally correlated,then one might gather information of one photon after carrying out monitoring on the other one,resulting in side-channel information leakage in some applications, e.g., the quantum key distribution, the quantum random number generator. Therefore, it is very important to obtain spectrally or frequently uncorrelated photon pairs. Usually, purity is used to characterize the correlation degree of a photon pair, and the higher the purity, the lower the correlation in frequency.

To date,different methods for improving the spectral purity of photon pairs have been put forward. For example,Mosleyet al.and Meyer-Scottet al.[5,6]proposed to improve the spectral purity by using narrow bandpass filters,since narrow bandpass filters can effectively filter out unwanted frequencies, and thus destroy the spectral correlations in SPDC sources.[7,8]However, narrow bandpass filters will inevitably bring into extra insertion loss, causing a lower photon counting rate in practical experiments.[6]Moreover,it is difficult to make the spectral shape of each filter identically matched with the photons passing by,since they might come from different crystals.[9]In contrast,another good choice is to select proper nonlinear crystal,pumping laser,and phase-match conditions for improving the spectral purity.

There have been a lot of works addressing this aspect,and in general they can be divided into four categories: (i)to apply Gaussian approximation on the phase matching amplitude and then decompose the joint spectral amplitude (JSA)by selecting proper pump bandwidths and crystal lengths for spectral uncorrelation;[10-13](ii)to achieve frequency uncorrelated biphotons with group velocity matching (GVM)condition;[13-20](iii)to process optimizations by adjusting the ratio between the width of the pump envelope amplitude and the width of the phase-matching amplitude;[21](iv) to implement joint optimizations on both the pump bandwidth and the crystal length.[22]In this paper, we systematically study and summarize these existing methods, and further present improved techniques. By re-defining the formula of the ratio between the widths of the phase matching amplitude and the pump envelope amplitude, we can obtain an improved purity with the third method compared with former work. Moreover,by implementing the local search algorithm into the joint optimization process for the fourth approach,we can greatly reduce the time cost on searching the optimal values. We first describe the theory, then carry out corresponding numerical simulations,and finally discuss advantages and disadvantages of each method. To be noted, in principle, the introduced methods can be implemented on any kind of periodically poled nonlinear crystals. Here for simplicity, we just employ the periodically-poled potassium titanylphosphate(PPKTP)crystal and the periodically-poled lithium niobate (PPLN) crystal as examples for illustration.

2. Theory

For a collinear SPDC process, the signal photon and the idle photon are created by driving pump photon into a nonlinear crystal. At the output of the crystal,the biphoton state can be written as

By Schmidt decomposition,[23,24]JSA can be decomposed into the product of two orthogonal basis sets,μn(ωs) andυn(ωi),as

As a result, the spectral puritypof the biphoton state can be calculated by

The PEA can be described by a Gaussian function as

whereωp0andσpare the central frequency and the bandwidth in frequency of the pump photon.σpcan be converted into the bandwidth in wavelength Δλby

whereλpis the wavelength of the pump. Due to the energy conservation

whereωs0andωi0are the central frequencies of the signal photon and idle photon,and we can obtain

whereνsandνiare the frequency differences between their respective frequencies and central frequencies,i.e.,νs=ωsωs0 andνi=ωi-ωi0.

The PMA in a nonlinear crystal can be written as

whereLis the crystal length,and Δkis the difference between the wave-vectors. The wave-vector is given by

wherenis the refractive index. And the difference between the wave-vectors in s periodically poled crystal can be written as

whereΛis the poling period of the periodically poled crystal.

2.1. Uncorrelation obtained from JSA

To reach spectral uncorrelation, the spectral distribution of PEA and PMA should be concentrated near the central frequency. Compared with sinc function, Gaussian function has less sideband. We can use the Gaussian approximation(sinc(x)≈e-γx2,γ= 0.193) to replace the sinc function of PMA,then JSA is updated with

For Eq. (15), to acquire the spectrally uncorrelated state, the last item of the equation should be eliminated,thus we have

Given determinate wavelengths of pump,signal,and idler,we can select the suitable pump bandwidth and crystal length to make Eq. (16) hold. As a result, the spectrally uncorrelated state can be achieved.

This is the first method on how to improve the photon purity.It is easy to understand,and can also help us to learn other methods.Moreover,as long as Eq.(16)holds,it should satisfy

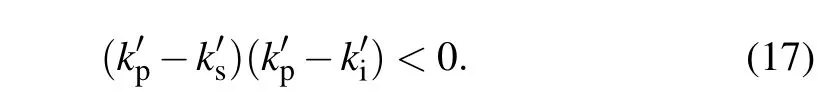
That is to say, the group velocity of the pump should lie between the group velocities of the signal and the idler.

Graphically, the width of PEA’s contour is in proportion to the pump bandwidth, and the angle between the contour line and theXaxis is 135°due to the law of energy conservation.[15]Here the width of PMA’s contour is inversely proportional to the length of the crystal. And its pinchθis not a fixed value and can be calculated. The tangent for the pinch of PMA can be defined as

When Eq.(17)holds,the pinch of PMA will be positive.

2.2. Engineering with the group velocity matching condition

We now discuss the second method,to engineer with the GVM conditions.[25-27]GVM conditions can be applied on the pump pulse and at least one daughter photon. The photon pairs are generated in the spectral mode,where the velocity of the pump photon is equal to the group velocity of one daughter photon or the average group velocity of both daughter photons.[5]As a result, spectrally uncorrelated biphoton state and pure heralded single photon are directly generated at several fixed wavelengths. There are three types of GVM conditions[18]

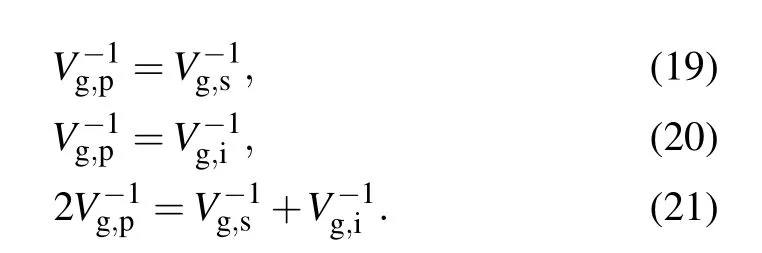
Equations (19)-(21) are symbolically represented by GVM1,GVM2, and GVM3, respectively. And they are individually consistent with

2.3. Uncorrelation by adjusting the width ratio

As addressed in Ref.[28],the formula of JSA can be decomposable only when doing approximation on PMA with Gaussian function,and the purity reaches its maximum value whenξ=1. However,without Gaussian approximation,the purity may not be optimal whenξ=1.

Below let us present an improved method on increasing the photon purity. Considering that the expression ofξin Eq.(27)is asymmetric for the signal and the idler,we re-define an intermediate variableζ,

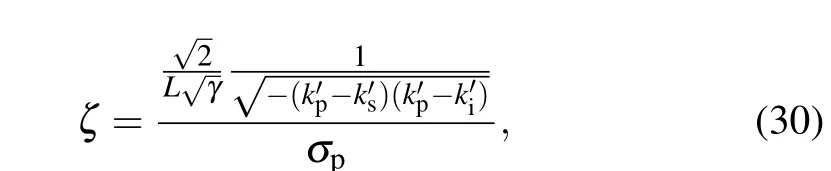
Obviously, hereζis only related with the pump wavelengthσpand the crystal lengthL. Then the optimal experimental conditions can be found to get the maximum purity.

2.4. Joint optimization of both the pump wavelength and the crystal length

The fourth method is to directly implement joint optimizations on the pump bandwidth and the crystal length in order to obtain the highest purity value within certain spectral ranges. Here we propose to implement the local search algorithm(LSA)into the joint optimization process to replace the trivial exhaustive search method, which can simplify akdimensional optimization problem intokone-dimensional optimization problems, greatly reducing the time to search for the optimal values. Though the purity is not able to reach 1 even after applying this method, a proper interference filter can be employed to narrow the bandwidth and further improve the purity.

3. Simulation

Second-order nonlinear optical materials are excellent platforms for quantum optics. For example, potassium titanylphosphate(KTP)and lithium niobate(LN)not only have excellent second-order/third-order nonlinear coefficient and electro-optic effect, but also possess very mature technology on waveguide fabrication. These merits make them very promising candidates for applications in parametric downconversion, frequency conversion, modulation processes, etc.Here for simplicity,we take periodically poled KTiOPO4(PPKTP)and periodically poled lithium niobate(PPLN)crystals as examples for descriptions. Their refractive index and Sellmeier equations are referring from Refs.[30,31].

For the first method addressed in Section 2, in order to satisfy the condition(17),we consider the case of type-I nondegenerate PDC. Moreover, for practical application requirements, one of the daughter photons is assumed being located in the communication band(1.3 μm-1.55 μm),then the range of the pump wavelength should lie within 546 nm-632 nm for PPLN and in the range of 756 nm-797 nm for PPKTP.For easy description, we first choose PPKTP as an example,the central wavelengths are chosen as 552 nm,857.3 nm,and 1550 nm, for the pump, the signal, and the idler photons, respectively. Then the period of the periodically poled is calculated asΛ= 11.6604 μm,k′s-k′p= 5.782×10-12s/m,andk′i-k′p=-1.507×10-10s/m. To satisfy Eq. (16),σpL=1.0906×1011Hz·m. If the pump bandwidth Δλand the crystal lengthLare set as 1.5915 nm and 1.1077 cm, respectively, the purity will be 0.99967 when applying Gaussian PMA,while the purity will be 0.96931 when implementing sinc PMA.Accordingly,we plot out corresponding PMA,PEA,and JSA in Fig.1. Besides,we choose another example of PPLN,the central wavelengths of the pump,the signal,and the idler are set as 775 nm, 1320 nm, and 1877 nm, respectively. Here,Λ=20.4014 μm,k′s-k′p=2.014×10-11s/m,andk′i-k′p=-2.488×10-11s/m. Accordingly, we obtainσpL=1.4379×1011Hz·m. When the pump bandwidth Δλand the crystal lengthLare 3.1831 nm and 1.4394 cm,respectively, the purity is 0.99877 with Gaussian PMA and 0.94746 with sinc PMA.Corresponding PMA,PEA,and JSA are shown in Fig.2.

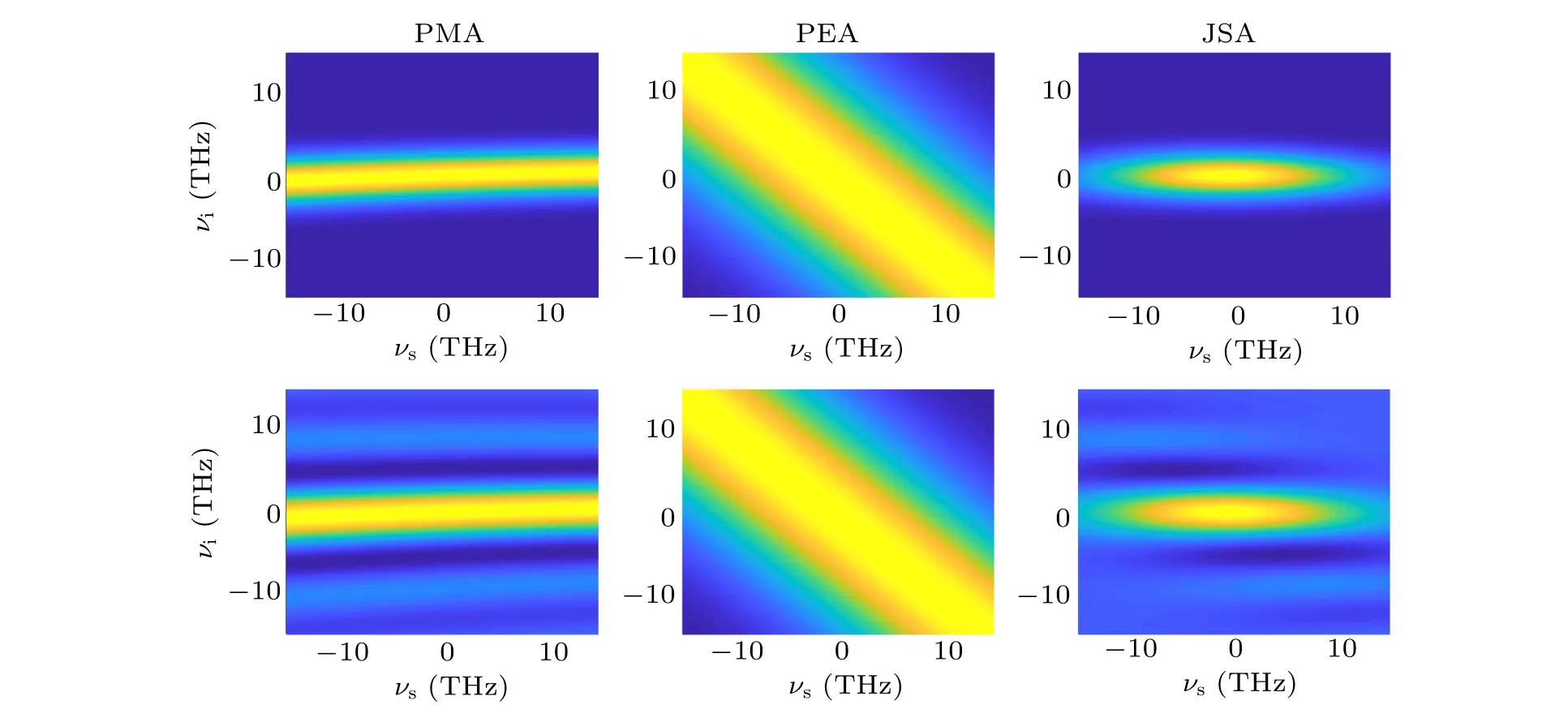
Fig.1. The contours of PMA,PEA,and JSA in PPKTP simulating with the first method. The biphoton is generated from type-I 552 nm(o)→857.3 nm(e)+1550 nm(e), when the bandwidth Δλ and the crystal length L are 1.5915 nm and 1.1077 cm, respectively. When PMA is approximated as Gaussian function,PMA,PEA,and JSA are shown in the first row,and the purity is 0.99967. When PMA is adopted with sinc function,PMA,PEA,and JSA are shown in the second row,and the purity is 0.96931.

Fig.2. The contours of PMA,PEA,and JSA in PPLN simulating with the first method. The biphoton is generated from type-I 775 nm(e)→1320 nm(o)+1877 nm(o),when the bandwidth Δλ,the crystal length L,and temperature are 3.1831 nm,1.4394 cm,and 30 °C,respectively.When PMA is approximated as Gaussian function, PMA,PEA,and JSA are shown in the first row, and the corresponding purity is 0.99877.When PMA is adopted with sinc function,PMA,PEA,and JSA are shown in the second row,and accordingly,the purity is 0.94746.

For the second method, we consider type-II degenerate SPDC.We find that GVM1is satisfied when the pump wavelength is 612 nm and GVM3is satisfied when the pump wavelength is 791 nm in PPKTP crystal. For GVM1or GVM2, a long crystal can be employed to improve the purity. When the pump wavelength is 612 nm,the pump bandwidth and crystal length might be chosen as 2 nm and 3 cm,respectively,accordingly,the purity is 0.98463 and its JSA is shown in Fig.3(a).For GVM3,the pump bandwidth and crystal length can be selected by following Eq. (16). With the pump wavelength of 791 nm, the pump bandwidth and crystal length can take the values of 0.51 nm and 1 cm, respectively. Then the purity is 0.81429 and its JSA is shown in Fig.3(b).

Now, let us see the third method presented in Section 2,where GVM3is assumed to be satisfied. We analyze the relationship betweenξdefined in Eq. (27) and purity for two different types of PMAs, as illustrated in Fig. 4(a). It shows that the maximum purity can reach 1 whenξ=1 for Gaussian shaped PMA. However, for sinc shaped PMA, the purity just reaches its maximum value whenξ=1.14 and its maximum purity is 0.8146.Obviously,it only results in poor purity.Now let us see our improved method, the relationships betweenζdefined in Eq.(30)and purity are displayed out for two different types of PMAs, see Fig. 4(b). For easy description, here we use type-I 775 nm→1320 nm+1877 nm in PPLN as an example. As we can see from Fig.4(b),the purity reaches its maximum for the sinc shaped PMA whenζ=1.21, and its maximum value is 0.97924, where the pump bandwidth Δλand the crystal lengthLare 3.1831 nm and 1.1896 cm,respectively. Compared with the above maximum purity 0.8146,our modified method shows significant improved purity.

Fig. 3. The contours of JSA for different wavelength matchings simulating with the second method. (a) The biphoton is generated from type-II 612 nm(o)→1224 nm(e)+1224 nm(o)in PPKTP and the purity is 0.98463, when the bandwidth Δλ and the crystal length L are 2 nm and 3 cm. (b) The biphoton is generated from type-II 791 nm(o)→1582 nm(e)+1582 nm(o)in PPKTP and the purity is 0.81429,when the bandwidth Δλ and the crystal length L are 0.51 nm and 1 cm.

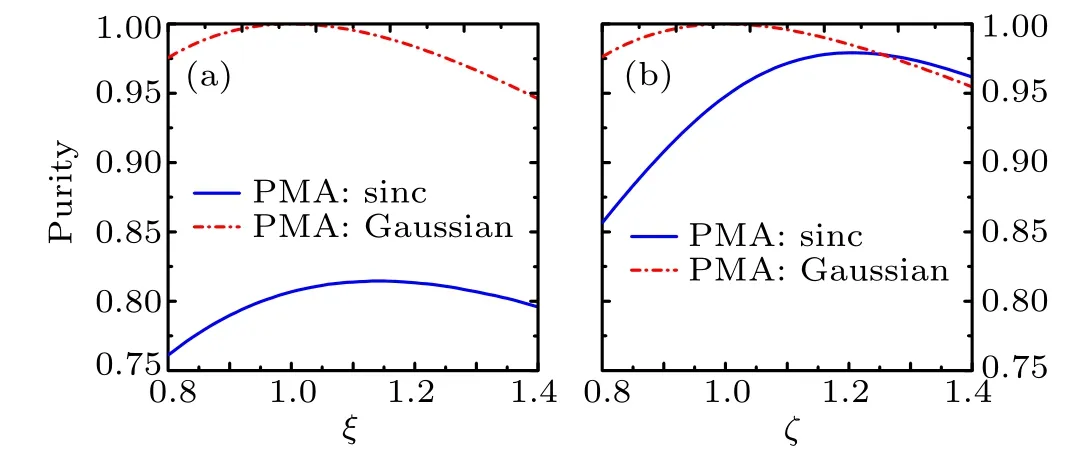
Fig.4.(a)The relationship between ξ and purity for Gaussian PMA and sinc PMA with GVM3. (b) The relationship between ζ and purity for Gaussian PMA and sinc PMA for type-I 775 nm→1320 nm+1877 nm in PPLN with the improved third method.

For the fourth method, considering it does not need to satisfy any limitations on either inequality(17)or GVM conditions, it is a more general approach and has robust applications. For easy description,we use type-I PPKTP as an example, where the central wavelengths of pump, signal, and idler are set as 552 nm, 857.3 nm, and 1550 nm, respectively. We carry out jointly optimizing on both the pump band width and the crystal length,corresponding simulation results are shown in Fig.5. From Fig.5,we find that the purity can reach up to 1 after full parameter optimizations. If taking practical processing difficulty into account, we can select compromised pump bandwidth Δλand crystal lengthL, e.g., 2 nm and 8.8 mm,respectively, and the corresponding purity is 0.94569. Obviously, the fourth method is not only easy to implement, but also can show excellent performance.

Fig. 5. Joint optimization of the pump bandwidth and crystal length with the fourth method. Meanwhile,the central wavelengths of pump,signal, and idler are 552 nm, 857.3 nm, and 1550 nm, respectively in type-I PPKTP.Different color represents different purity,and the value of purity represented by the color has been marked on the right column.

In addition,we also carried out calculations for other nonlinear crystals or phase-matching conditions,e.g.,type-II BBO or type-0 PPLN, by implementing the above four methods.However, the obtained purities are in general quite low when without using filters. Therefore,we did not list them out in the simulation part.

4. Conclusion

Focusing on collinear and single mode SPDC and neglecting transversal and multi-mode effects,we have discussed four methods on how to improve the purity of down-converted photon sources. The first method is to derive from JSA function, through which we can obtain the relationship between the pump bandwidth and the crystal length for spectral uncorrelation. The second method is taking advantage of GVM conditions. The third method is to adjust the width ration of PEA and PMA under GVM3condition,without doing any approximation on PMA functions.The fourth method is to apply joint optimization on both the pump bandwidth and the crystal length without doing any approximation or assuming any GVM condition.For the first three methods,they need to meet certain applicable conditions, e.g., it needs to satisfy the inequality for method 1 or method 3; and the second method only works when satisfying one of the GVM conditions. For the fourth method, it does not assume any applicable conditions, while for some phase-matching conditions, sometimes resulting in moderate purities without filters. Therefore, different methods have their advantages and disadvantages, and a proper method should be chosen when people design their experimental parameters. We believe our work could provide valuable references for the generation and application of high purity single-photon sources in the fields of quantum information and quantum optics.