钢筋混凝土双曲拱桥计算模型修正方法

王浩宇， 淳庆

(东南大学 建筑学院， 江苏 南京 210096)

钢筋混凝土双曲拱桥是我国六七十年代特殊国情背景下兴起的一种特殊结构类型的拱桥，它有着结构轻巧、用料较少、造型极具民族特色、施工快速等诸多优点，但是限于当时荷载等级和设计水平较低，大多沿用至今的双曲拱桥都存在各种残损病害，亟需对其进行加固修缮.

在国外，由于实际工程的缺乏，大多学者研究的对象都是石制单向拱桥，如Cavalagli等[1]对多种几何尺寸的砌体拱桥进行的安全性分析，Pepi等[2]对砌体古桥的动力特性分析等.目前，国内的一些学者也利用有限元方法研究双曲拱桥.如陈旭勇等[3]通过理论计算和ANSYS有限元模拟来研究双曲拱桥加固前后的结构性能对比；赵人达等[6]、张向东等[7]利用平面杆梁单元模拟主拱圈、空腹及实腹段；刘加湾等[8]、漆泰生等[9]用空间梁单元模拟主拱圈及空腹墙，填料则结合空间杆单元模拟，横向拱波及桥面板用空间板单元；徐家云等[10]、王敏强等[11]用实体单元模拟主拱肋，横向拱波，空腹墙等，并根据具体问题作适当简化；程章宏等[12]将拱波拱肋通过等效得到一种等效的模型截面，从而用梁单元直接模拟拱波和拱肋，并用杆单元模拟填料，桥面板用等效格子梁方式建模.

综上，国外学者研究的拱桥完全不同于中国的双曲拱桥，而国内学者偏重于双曲拱桥的受力性能研究.关于双曲拱桥的模型修正方法研究鲜有报道.鉴于此，本文将以南京长江大桥双曲拱桥为例，对双曲拱桥的模型修正方法进行研究.

1 双曲拱桥有限元模型建立

1.1 实体单元模型的建立

南京长江大桥被列为中国第一批工业遗产保护名录，其公路桥共有33孔双曲拱桥，包括北岸4孔、南岸18孔和回龙桥11孔；每孔双曲拱的主拱圈由预制的混凝土构件和工地现浇的混凝土结合而成，即下层由预制的16根拱肋和15跨拱波拼成，拱波上表面浇筑6 cm的现浇钢筋混凝土面层.

文中以南京长江大桥双曲拱引桥为例(图1)，通过有限元模型计算结果与双曲拱桥现场测试结果[16]的对比分析，研究适合于双曲拱桥性能计算的有限元模型修正方法.

(a) 外侧 (b) 内侧

主拱圈的简化是通过面扫掠线形成体的方式来对主拱圈进行建模，主拱圈中央截面简化为一个矩形，减去了15个半圆弧与矩形的和.拱肋之间的横杆无需再单独建立，一是考虑到主拱圈截面在原拱波处模拟的厚度偏大，此处横向刚度的增加正好对应连杆所具有的一定横向刚度；二是由于如果需要完全精细化模拟，连杆的尺寸相对于拱肋过小，在划分网格时相接处会产生大量的细小的网格，增加了计算量.

南京长江大桥双曲拱桥单跨的实体单元模型，如图2所示.模型选用的单元Solid 65(共650 639个)，结构阻尼比为0.05，混凝土选用C30混凝土，抗压强度为30 MPa，弹性模量为30 GPa，密度为2 350 kg·m-3，泊松比为0.3；拱顶填料弹性模量为19 GPa ，密度取天然砂砾石的堆积密度1 374 kg·m-3，泊松比为0.3.

图2 双曲拱桥的实体单元有限元模型

1.2 梁杆单元等效模型的建立

将拱肋拱波组成的主拱圈截面进行等效[12]，得到简化后等效的主拱圈截面，如图3所示.在ANSYS中导入等效的拱肋截面，通过创建等效截面的各个点，点连线，线围成面的方式完成等效拱肋截面的绘制，并将其存入作为一号梁截面.然后，建立拱轴线上的关键点，查《公路桥涵设计手册： 拱桥(上册)》可以得到拱轴线上各个点的坐标与跨高的比值[13].最后，将关键点连线并复制出所有的拱肋，横向联结每一个节点得到横向单元，至此完成等效的主拱圈的建模.

(a) 拱肋拱波原截面 (b) 等效后的截面(中间拱和边拱)

双曲拱桥的上部结构由空腹墙、墙上的空腹拱、拱顶填料和桥面板构成.由于拱顶填料只是负责传递桥面荷载，所以只需用受压杆单元模拟即可；空腹墙转化为立柱的形式，立柱沿横向设置联系梁；墙上的空腹拱横向间同样也设置联系梁；桥面板采用等效格子梁的方式建模，除了拱顶填料其余构件均采用空间梁单元模拟.

南京长江大桥双曲拱桥单跨的ANSYS有限元模型，如图4所示.模型左右两侧完全固定，梁单元选用Beam 188(共16 800个)，杆单元选用Link 180(共2 410个)结构阻尼比为0.05，混凝土选用C30混凝土，抗压强度为30 MPa，弹性模量为30 GPa，密度为2 350 kg·m-3，泊松比为0.3；拱顶填料弹性模量为19 GPa ，密度取天然砂砾石的堆积密度1 374 kg·m-3，泊松比为0.3.

图4 双曲拱桥的梁杆单元有限元模型

2 静动力分析

2.1 有限元模型静力分析

为证明有限元模型计算的有效性，将模型计算数据与现场实测数据进行比较.选取两种典型的工况进行分析，工况一为按跨中断面正弯矩最不利加载位置对称加载，工况二为按拱脚断面负弯矩最不利加载位置偏心加载.图5为不同工况下的荷载布置，表1为模型计算及现场实测的数据[16].表1中：模型1为梁杆单元模型；模型2为实体单元模型.

(a) 工况一车辆横向布置图 (b) 工况一车辆纵向布置图

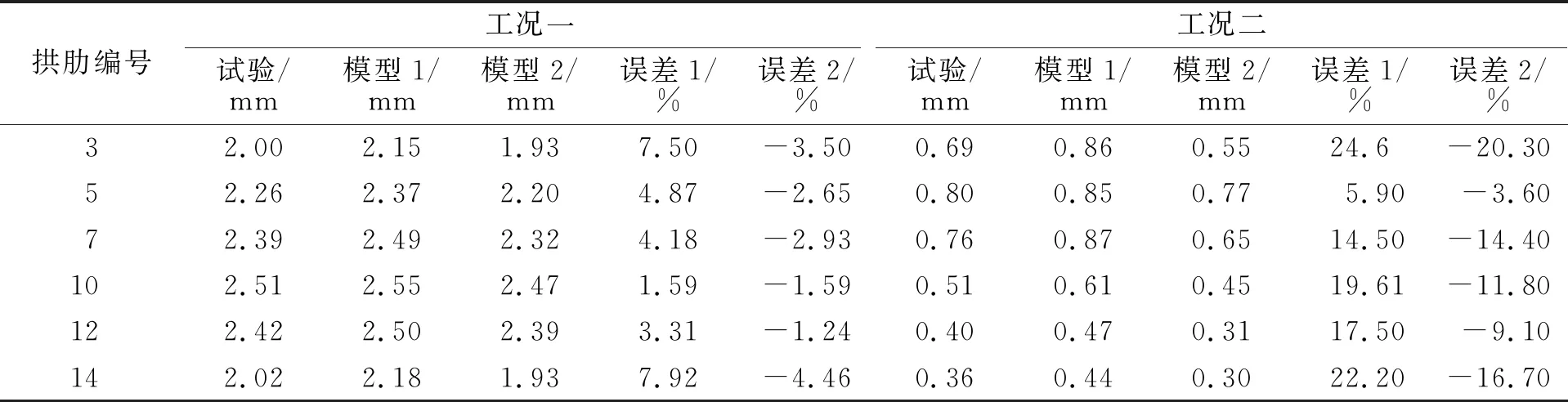
表1 有限元计算及现场实测的L/2处竖向挠度

由表1可知：梁杆单元模型的竖向挠度总体上要比现场试验结果稍微的偏大一些，靠近边跨的地方误差较大，在跨中误差较小，总体误差范围为1.59%～24.60%；实体单元模型的竖向挠度在跨中部分与现场试验值吻合较好， 总体误差范围为1.59%～20.30%.但是能够看出的是， 实体单元模拟的模型刚度稍稍偏大，计算挠度值都小于现场实测的数据.这主要是因为在主拱圈的等效过程中加厚了拱波的厚度，使其具有了一定的竖向承载能力，参与了结构竖向的承载增加了结构的竖向刚度.另外，因为ANSYS中实体单元建模等于各个构件之间默认刚接，所以增大了模型的刚度，从静力分析来看，实体单元模型比梁杆单元模型更加准确.

2.2 有限元模型动力特性分析

计算分析梁杆单元模型和实体单元模型的动力特性，将双曲拱桥有限元模型的前3阶自振周期、自振频率及振型描述与现场实测结构动力特性[17]进行对比，结果如表2所示.表2中：n为振型阶次.

表2 双曲拱桥有限元模型与实测的结构动力特性对比表

由表2可知:现场测试的单跨双曲拱桥基频为3.45 Hz，第一阶振型为竖直方向上的弯曲振动，第二阶振型为横向的扭转振动，第三阶振型为沿桥纵向的扭转振动.模型计算结果与现场测试结果的对比显示，采用梁杆单元模拟的双曲拱桥，前三阶固有频率都要略微小于现场实测值，总体误差为2.5%～18.9%，说明其竖向抗弯与纵横方向上的抗扭刚度都较为明显地低于实际情况.

实体单元模型计算结果与现场实测结果较为复合.从固有频率看，前三阶固有频率实体单元模型大于现场数据，总体误差为2.0%～4.9%；从振型上看也基本吻合，一阶振型是沿横向的扭转振动，二阶振型是沿纵向的扭转振动，三阶振型是竖向的弯曲振动.这说明梁杆单元模型较真实情况存在着刚度的缺失，而实体单元模型由于较为精细地模拟了双曲拱桥，所以动力特性与实际情况基本吻合.

2.3 模型的选取

实体单元模型由于是精细化模拟，所以与实际情况最为接近，模型的静、动力特性也就最准确.但它的缺陷也十分明显，网格划分过多导致的结果使得计算时间变长，计算效率低下.因此，选取修正的模型是梁杆单元等效模型，使其静动力特性更加接近实际情况，从而满足后续计算效率与精度的要求.

3 有限元模型的改进方案

3.1 修正等效模型建立

由上可知，梁杆单元模拟的等效模型计算结果与实测数据存在25%以内的误差.在等效过程中，首先等效的拱肋截面在原拱波拱顶处是圆弧面，立柱模拟的空腹墙可能在与主拱圈交接处存在着较大的空隙，从而会影响到结构的整体刚度；其次，上述方法忽略了空腹式拱桥拱上建筑与主拱圈的联结作用，这种联结作用也能够很好的增强模型的整体刚度；最后，用等效的格子梁来代替桥面板，并不能很好地反应桥面板纵横方向上的抗弯、抗扭刚度，等效的格子梁只能够简单地代替桥面板起到竖向传力作用和一些纵横方向上的刚度.据此，需要对等效模型进一步修正.

1) 考虑立柱模拟的空腹墙与主拱圈相接处可能存在空隙导致整体刚度的缺失，根据实际情况，拱波现浇层上部为水平线，将等效的拱肋截面最顶部改为平面.

2) 拱上建筑与主拱圈的联结作用的模拟是在同一排立柱之间加上斜撑，由于同一排空腹墙在其顶部有着拱形墙连接，这部分墙体在单用立柱模拟时并没有被表现，因此，需要增加斜撑来增加同一排柱的关联性，弥补缺失的抗侧刚度.抗侧刚度公式[18]为

(1)

式中：K为抗侧刚度；h为墙的高度；b为截面长度；G为剪切模量；A为截面面积.

每根斜撑的截面应由其模拟的墙截面来定.斜撑的加入同时也加大了空腹墙与主拱圈的接触面积，以模拟拱上建筑与主拱圈的联结作用.

3) 用壳单元模拟桥面板来代替等效格子梁模拟桥面板，其厚度设置为空腹拱顶部至桥面的距离为40 cm，壳单元模拟桥面板更加的符合实际情况.另外，杆单元与梁、壳单元耦合时，有公共节点即可无需约束方程；梁单元与壳单元耦合时，由于自由度数目相同，自由度也相同，所以也无需约束方程.

修正后的南京长江大桥双曲拱桥单跨梁杆单元模型，如图6所示.模型中除了等效拱肋截面更改以外，其余截面参数都不变.梁单元选用Beam 188(共89 063个)，杆单元选用Link 180(共35 20个)，桥面板单元采用Shell 81(共1 433个)，结构阻尼比取0.05，混凝土选用C30混凝土，抗压强度为30 MPa，弹性模量为30 GPa，密度为2 350 kg·m-3，泊松比为0.3； 拱顶填料弹性模量取19 GPa， 密度取天然砂砾石的堆积密度1 374 kg·m-3，泊松比为0.3.

图6 修正后的双曲拱桥梁杆单元有限元模型

3.2 参数灵敏度分析

对重新建模后的模型进行模态分析后，发现仍然存在一定的刚度缺失，固有频率虽然有所提高，但是与现场实际测试结果仍存在较大的出入.因此引入参数的灵敏度分析，对重新建模后的模型进行修正.根据现场试验结果和理论的频率值构造目标函数[19]为

.

(2)

式中：F为目标函数；λai为频率有限元计算值；λti为现场实测频率；αi为各阶自振频率权重系数.

修正参数的选取将直接关系到有限元模型修正的成败和优化效率，应遵循2个基本原则：1) 选取的参数数量不能过多，参数数量太多将导致分析和优化的工作量增加，并且使优化迭代陷入局部最优解；2)结合工程经验选择灵敏度较高的参数.因此，本研究选取桥面板厚度、混凝土弹性模量、密度等作为设计参数，并进行灵敏度分析.目标函数对设计变量的灵敏度为

(3)

用ANSYS中的最优梯度法对设计参数进行灵敏度分析，得到模型中设计参数的变化，以及目标函数灵敏度.结果表明：目标函数对混凝土弹性模量、混凝土密度和桥面板厚度等设计参数的灵敏度分别为7.0%，6.1%和2.3%.说明，混凝土弹性模量和密度对于频率的计算结果影响很大，桥面板的厚度也有较大的影响.因此，将混凝土的弹性模量、密度和桥面板的厚度选取为待修正的设计参数.

3.3 模型修正计算结果

将修正后的梁杆单元模型的计算结果与现场实测结果的进行比较，结果如表3所示.表3中：n为振型阶次.优化迭代后的设计参数修正值，如表4所示.表4中：Ec为混凝土弹性模量；ρ为混凝土密度；hB为桥面板厚度.

表3 修正后的梁杆单元模型与现场实测的动力特性对比

表4 设计参数修正值与初始值

从表4可知：混凝土的弹性模量比原选取值增大21.67%.材料弹性模量的增大表征的是对整个结构的刚度的修正，说明初始计算模型的结构刚度存在不足；混凝土的密度的增加是与混凝土中的配筋率和施工时的均匀程度有关；桥面板厚度的增大也说明了等效格子梁模型并不能较好的模拟桥面板受力情况，采用壳单元模拟桥面板能够弥补刚度的缺失.

修正后梁杆单元模型的模态振型，如图7所示.从图7可知：修正后的等效模型比初始模型整体刚度要大，竖向抗弯与纵向抗扭刚度有较为明显的提升，自振周期明显降低，振型与实际情况基本一致.

(a) 修正后模型的一阶振型 (b) 修正后模型的二阶振型 (c) 修正后模型的三阶振型

3.4 静力分析验证

修正后的梁杆单元模型增大了整体刚度，更加符合实际情况.对修正后的梁杆单元模型在两种工况下的竖向变形进行计算分析，其计算结果与现场实测结果的比较，如表5所示.表5中：模型A为未修正的模型，模型B为修正后的模型.

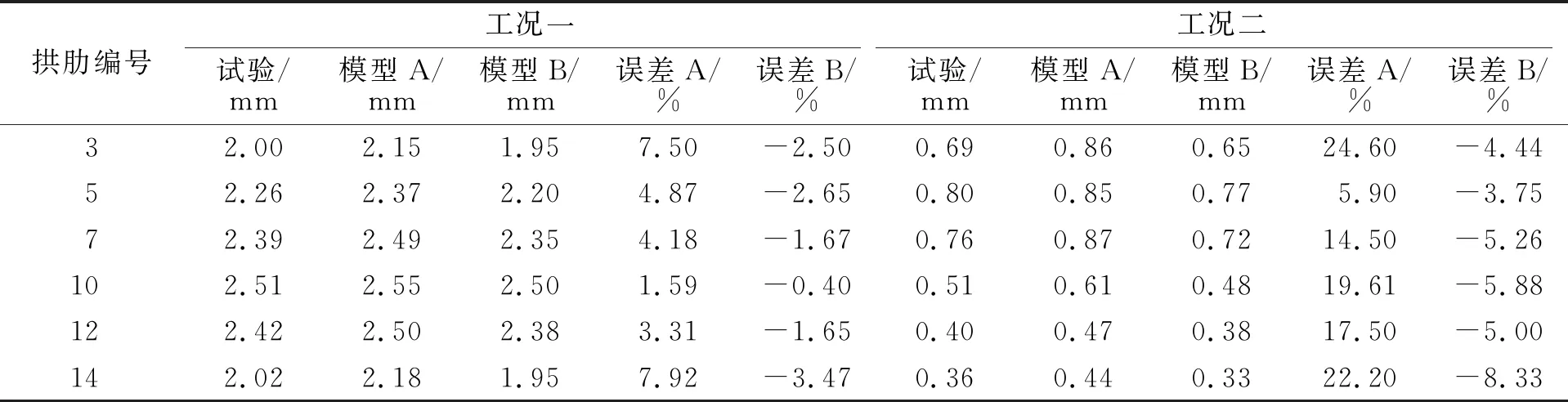
表5 修正后的梁杆单元模型与现场实测的L/2处竖向挠度对比

由表5可知：修正后的梁杆单元模型计算结果与现场实测结果更加接近，误差为0.40%～8.33%.说明，修正后的模型达到较高的计算精度，能够较为准确地反映该双曲拱桥真实的结构受力状况.

4 结论

通过对钢筋混凝土双曲拱桥有限元建模方法的研究，以及与现场实测结果的对比分析，可以得出以下3点结论.

1) 双曲拱桥采用梁杆单元模型进行静力计算时，其总体误差范围为1.59%～24.60%；而采用实体单元模型计算时，其总体误差范围为1.59%～20.30%.采用梁杆单元模型进行动力计算时，其总体误差为2.5%～18.9%；而采用实体单元模型计算时，其总体误差为2.0%～4.9%.

2) 由于在模拟时的各种简化导致双曲拱桥梁杆单元模型存在较大的刚度缺失，计算结果精度要略差于实体单元模型.考虑到梁杆单元计算的效率与建模难度等因素，在建模方式上对梁杆单元模型进行一定的改进，并通过参数灵敏度分析的方法，对计算模型进行了混凝土弹性模量、混凝土密度和桥面板厚度的参数修正.修正后的梁杆单元模型静动力计算结果与现场实测结果较为吻合，并且各阶模态振型也较为接近实测值，静力计算误差在8.33%以内，动力计算误差在2.07%以内.因此，提出的梁杆单元模型在修正后达到较高的计算精度.

3) 所提出的适用于钢筋混凝土双曲拱桥有限元模型修正的方法，其研究结果可以为钢筋混凝土双曲拱桥的建模方法、模型修正和科学计算提供依据，建议在后续研究中采用更多的工程实例进行验证.